一种采用非均匀量化的近似Log-MAP算法

周继宇，张雅奇，徐伯庆

(上海理工大学光电信息与计算机工程学院，上海200093)

0 引言

Turbo译码器中主要采用最大后验概率(MAP)和软输出Viterbi(SOVA)2类软译码算法。其中，MAP算法因对栅格图中的所有路径进行双向比较来获取信号的后验概率，故具有较高的译码精度。MAP算法早在1974年就已经由Bahl等人提出，由于该算法中存在大量指数运算，不利于硬件实现。后来Robertson及Erfanian等人提出Log-MAP算法作为改进，将指数运算转化为求最大值和校正函数的运算，得到的纠错性能与MAP算法等价。若忽略Log-MAP算法中的校正函数，即为Max-Log-MAP算法，它大大简化了计算，但是译码精度较Log-MAP算法要低0.3～0.5 dB，通信容量降低7% ～10%。

目前，实际应用中都是用查表来计算Log-MAP算法中的校正函数，即将校正函数所有的可能值存放在一个额外的外存储单元中。这样做，译码性能很好，却很大程度地增加了Turbo译码器的成本。因此，这里采用非均匀量化的方法来对校正函数做区域近似，以期望在减小成本开销的同时，尽量获得较好的译码性能。

1 Log-MAP算法原理

图1为一个MAP软译码器单元，它的输入有外信息Le(uk)，系统信息和校验信息的复用序列(即=(y1，y2，…yk，…yN)，其中 yk=(，))，输出为对数似然比信息L(u)。k

图1 MAP译码单元框图

MAP译码器的任务就是求解L(uk)，然后通过硬判决，得到原信息uk的最大似然估计u^k:

那么首先就需要计算原信息uk的对数似然比:

根据Bayes规则和BCJR算法推导式(2)可得:

至此，只要赋予前向度量和后向度量的初始值，便可递推出任意时刻k的ak(s)和βk(s)的值，从而实现式(3)的求解。以上为标准的MAP算法求解过程，Log-MAP算法为了简化计算，令:

代入式(3)可得:

又存在 Jacobian函数［6］:

再将式(5)代入到式(4)的分子、分母中即可完成简化计算的目的，fc(·)就是校正函数，也是Log-MAP算法计算的重点。

2 校正函数的非均匀量化

2.1 确定校正函数的量化区域

表1 栅格路径的统计数据(编码器寄存器个数为3)

从表1中可以看到，在时刻k，对于所有的8个寄存器状态，超过半数的栅格路径的x值大于4，即Turbo迭代译码中，绝大多数x＞4。因此，选取自变量 x的量化范围为［0 4］，当 x ＞4时，fc(·)＜ 2 ×10－2，在计算时，可以作零值处理。

2.2 非均匀量化过程

首先，将纵坐标y在0和0.693之间均匀地划分为 N个区间，得到的分段点分别为 y1，y2，…，yN－1。又因为 y=fc(x)=ln(1+e－x)，可求得yi(i=1，2，…，N－1)对应的横坐标分段点xi(i=1，2，…，N － 1)。

然后，分别在量化区间［0 x1］、［x2x3］、…、［xN－14］上使用拉格朗日中值定理:

可以求得在［xi－1xi］段上，fc(x)的量化函数。当然要对式(6)中的f(x)直接求积c分，很难实现，所以可以先利用麦克劳林公式:

将校正函数展开，得到一个可积函数后，再代入式(6)。综合考虑了计算复杂度和算法精度之后，这里采用五阶的展开式:

下面就以两电平和五电平量化为例，得到的各个区间上的量化，f函(数x)(［精0度0都.8取81 06.］0 00 1)。两电平量化时c在区间 上近似为0.504 5，在区间［0.8816 4］近似为0.115 3;五电平量化时，fc(x)在［0 0.299 9］上近似为0.621 9，在［0.299 9 0.662 5］上 近 似 为 0.482 5， 在［0.662 5 1.141 2］上 近 似 为 0.342 6， 在［1.141 2 1.906 1］上 近 似 为 0.200 8， 在［1.9061 4］上近似为0.059 8。

2.3 量化函数与校正函数的近似度比较

两电平和五电平非均匀量化函数分别与原校正函数的近似度比较如图2和图3所示。

图2 两电平量化

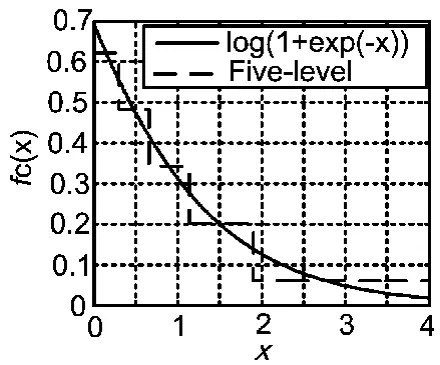
图3 五电平量化

3 仿真结果

基于上述对校正函数的非均匀量化分析，将两电平和五电平量化得到的近似函数用于Log-MAP算法，来实现Turbo码的迭代软译码。这里主要为编程实现对基于Log-MAP、近似Log-MAP和Max-Log-MAP算法的Turbo译码器仿真，并比较分析它们的译码性能。

这次仿真严格按照3GPP制定的LTE标准Release 9版本进行编程实现［5］，采用编码速率为1/3的 Turbo编码器。数据成帧发送，帧长为1 024 bit，信道为AWGN信道。图4为仿真得到的4种译码算法的误比特率曲线。

图4 AWGN信道Turbo译码器的BER性能比较(迭代3次)

4种译码算法的复杂度比较如表2所示。

表2 算法复杂度

4 结束语

采用非均匀量化的方法分别对Log-MAP算法中的校正函数进行两电平和五电平近似，并应用到LTE Turbo译码器中进行BER性能仿真。仿真结果表明:2种量化后的译码算法的纠错性能明显要优于Max-Log-MAP算法，而略逊于Log-MAP算法。然而在算法复杂度上，采用非均匀量化的近似Log-MAP算法却大大减少了Log-MAP算法的加法和查表次数，节省了硬件实现时，额外的存储开销。在降低Turbo译码器成本的同时，也获得了较好的译码性能。

［1］LIU Bin-bin，BAI Dong，MEI Shunliang.Variable nonuniform quantized belief propagation algorithm for LDPC decoding［J］.Journal of Electronics，2008，4：539 －543.

［2］ROBERTSONP，VILLEBRUNE，HOEHER P.A comparison of optimal and sub-optimal MAP decoding algorithms operating in the log domain［C］∥ proc of ICC’95，1995，3：1009 －1013.

［3］ERFANIANJ J A ，PASUPATHY S，GULAK G.Reduced complexity symbol detectors with parallel structures for it’s channels［J］.IEEE Transcations on Communications，1994，42：1661 －1671.

［4］LEE G，HYUN S，PARK S.Evaluation of the MAP Decoder for the Turbo coders of IMT-2000［C］∥IEEEVTS Fall 2000，2000，3：1266 －1269.

［5］Channel coding，multiplexing and interleaving［S］.3GPP TS36.212 V9.3.0，Release 9，2010 －09.

［6］SEIGO A.Algorithms for computations in Jacobian group of Cab curve and their application to discrete-log based public key cryptosystems［J］.IEICE Transpart，1999，8：1291－1299.

［7］张琳，刘星成.用于Turbo迭代译码的近似Log-MAP算法研究［J］.电路与系统学报，2006，3：70 －74.

［8］王新梅，肖国镇.纠错码-原理与方法［M］.西安：西安电子科技大学出版社，1991.