改进Min-sum的LDPC译码算法研究

吴 琼，梅进杰

(1.空军雷达学院研究生管理大队，湖北武汉430019;2.空军雷达学院，湖北武汉430019)

0 引言

低密度奇偶校验码(Low-density Parity Codes，LDPC)是由Gallager于1962年提出的一种基于稀疏校验矩阵的线性纠错码［1］。由于LDPC码具有较强的纠错能力、较大的灵活性和比较低的译码复杂度，在高斯白噪声AWGN信道下的译码性能可以逼近Shannon信道容量的极限，使它成为近年来纠错编码领域的研究热点之一。该文提出一种改进的Min-sum算法，利用最小差准则来计算该算法中的各个参数，有效提高了Min-sum算法中的性能。

1 Min-sum算法及其改进

1.1 LDPC码

LDPC码是由稀疏奇偶校验矩阵H(N－K)×N定义的线性分组码，其中码长为N，信息位为K，校验位为M=N－K，码率为R=K/N。则该码的校验矩阵H是一个M×N的矩阵，如果校验矩H中每一行有“ρ”个1，且每一列有“λ”个1，即H矩阵每行的行重相同，且每列的列重也相同，这种码称为规则(regular)LDPC 码［2］，记为 (N，λ，ρ)，否则称为非规则(irregular)LDPC码［3］。虽然非规则LDPC码的性能优于同等参数条件下的规则LDPC码，但是因为非规则码的实现复杂度很高，所以目前主要的研究对象还是规则LDPC码。式(1)给出了某个(8，2，4)LDPC码的校验矩阵H:

LDPC 码通常由双向图(也称 Tanner图［4］)表示，它是由变量节点(Variable node，矩阵的每行代表1个校验方程，每列代表1个码字)和校验节点组成的。其中变量节点分别与校验矩阵的各列相对应，校验节点分别与校验矩阵中的各行对应。如果1个码字比特包含在相应的校验方程中，就用1条连线将所涉及的比特节点和校验节点连起来，所以Tanner图中的连线数与校验矩阵中的1的个数相同。图1所示为式(1)所对应的Tanner图，其中X1－X8为变量节点，C1－C4为校验节点。

图1 矩阵H对应的Tanner图

1.2 Min-sum算法

对数域BP算法(LLR-BP)译码算法是最经典的LDPC解码算法之一，其核心思想就是利用Tanner图中的变量节点和校验节点之间的约束关系，在2种节点之间来回传递并更新置信度信息，最终实现解码。在每次迭代过程中，所有校验节点从相邻的变量节点接收信息，将这一信息处理后反馈给相邻的变量节点，然后变量节点再从校验节点反馈给相邻的变量节点，最后根据变量节点的信息进行判决。

LLR-BP译码算法是用LLR值作为迭代译码过程中传递的置信值的一种置信传播译码算法。与概率域BP算法相比，它将大量的乘法运算转化为加法运算，大大降低了译码算法的复杂度，并有效地减小了系统的时延。但是LLR-BP算法在迭代译码前需要估算信道噪声功率，并且在对校验节点进行信息处理时，非线性运算实现复杂度较高。

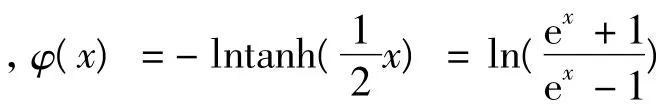
设编码器输出码字为 c=(c1，c2，…，cn)，采用BPSK调制方式后变为xi=2ci－1，通过AWGN信道后，译码器的输入序列为 k=(k1，k2，…，kn)，其中ki=2ci－1+mi，mi是均值为0、方差为σ2的高斯白噪声，译码得到的序列为c^=(c^1，c^2，…c^n)。Rj={I∶Hji=1}表示与校验节点j相连的变量节点的集合，Rj/i表示除去第i个节点以外其他与校验节点j相连的校验节点的集合，Ci={j∶hji=1}表示与变量节点i相连的校验节点的集合，Ci/j表示除去第j个校验节点以外其他与变量节点i相连的校验节点的集合，qij(b)表示变量节点i传递给校验节点j的外部概率信息;rji(b)表示校验节点传递给变量节点的外部概率信息;Pi(b)=P(ci=b|yi)表示接收到yi以后判断变量节点ci=b的概率。最小和算法的具体译码过程如下:

①似然信息初始化

计算信道传递给变量节点的初始概率似然比信息 L(pi)，i=1，2，…，n，对于变量节点 i以及与其相邻的校验节点j而言，在AWGN信道中变量节点传递给校验节点的初始信息为:

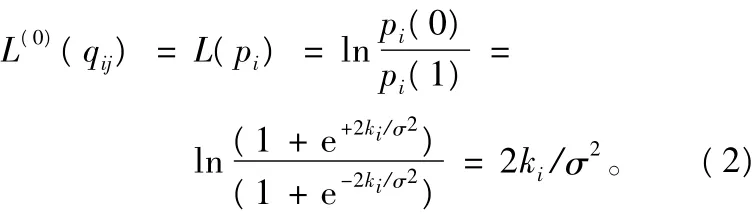
②水平迭代(校验节点的信息处理)

对所有的校验节点j和其相邻的变量节点i∈R(j)，第r次迭代时，计算变量节点传向校验节点的消息:

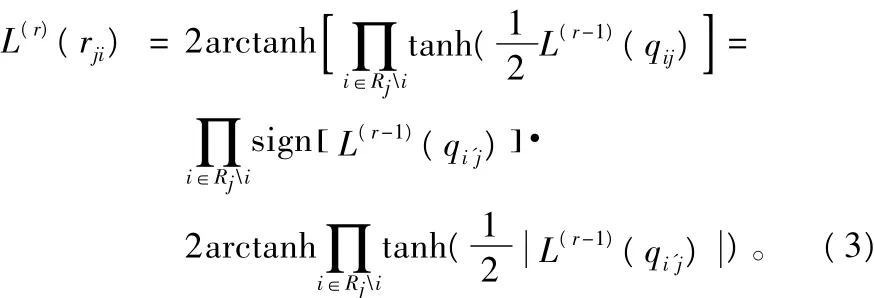
最小和算法对校验节点的信息更新公式做了如下近似简化:

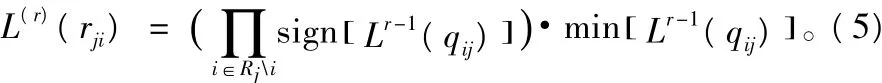
③垂直迭代(变量节点的信息处理)

对所有的变量节点i和其相邻的校验节点j∈C(i)，第r次迭代时，计算校验节点传向变量节点的消息:

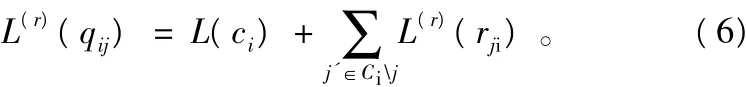
④译码判决

对所有变量节点结算硬判决消息

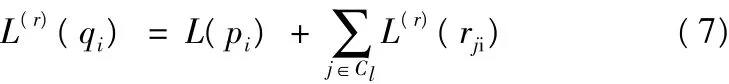
L(l)(qi)＞0，则c^i=0;否则为1。

⑤停止

判断Hc^iT=0是否成立，若成立则停止迭代，译码输出为c^i;否则返回步骤①继续迭代，直到达到最大迭代次数，同时给出译码失败标志。

1.3 改进的Min-sum算法

由于Min-sum算法与LLR-BP算法相比过高的估计了输出校验消息的幅度，如果采取措施降低消息的幅度，则可以接近甚至超过LLR-BP算法的性能，由此产生了Normalized BP-based算法和Offset BP-based算法。为了叙述方便，将式(4)中的L(r)(rji)记为L1，式(5)中的L(r)(rji)记为L2。

Normalized BP-based算法是通过将原来的幅度除以一个尺度因子α得到的，其中α＞1，称其为校正因子，此时校验节点的输出信息L(γ)(rji)更新为:

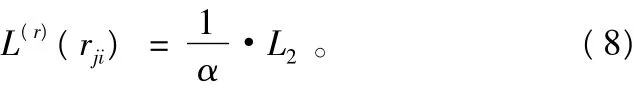
Offset BP-based算法是将原来的校验消息幅度减去一个数值β来降低，β称其为偏移因子，此时校验节点的输出信息L(r)(rji)更新为:

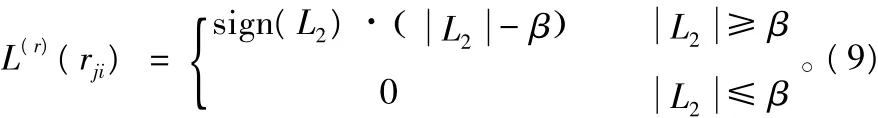
从式(9)和式(10)可以看出，由于Normalized BP-based算法和Offset BP-based算法分别通过引入单一的乘性因子和加性因子，从而只能一定程度上减小变量节点之间信息的相关性，对LLR BP算法的译码性能提升有限。如果能够同时引入乘性因子和加性因子，那么必然能够使得LLR BP算法的译码性能得到进一步提升。

该文对Min-sum算法进一步改进，通过同时引入α、β和γ，使得式(5)中不但含有乘性因子而且还有加性因子，从而进一步减小变量节点之间信息的相关性，提高Min-Sum算法的译码性能。

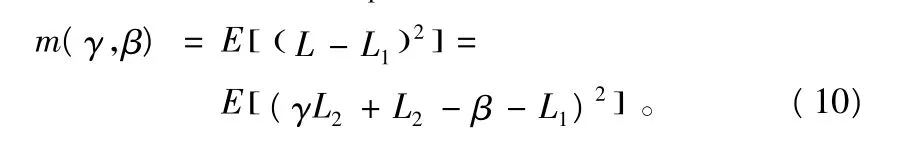
为了确定γ和β的值，使得m(γ，β)达到最小值，分别对式(10)中的γ和β求偏导数，得出:

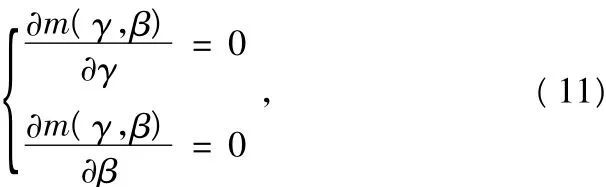
将式(10)代入式(11)可得:

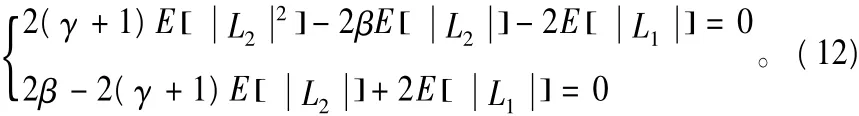
解得:

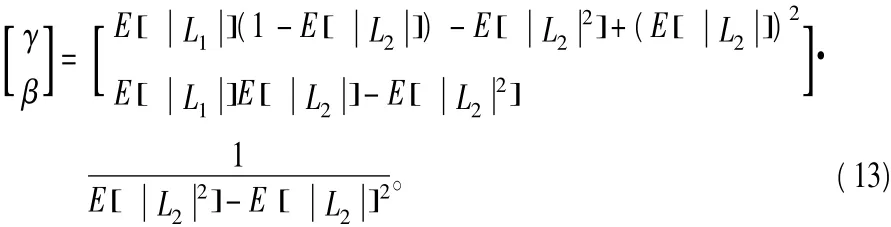
综上所述，改进的Min-sum算法校验节点的信息更新公式可以用下式进行描述:

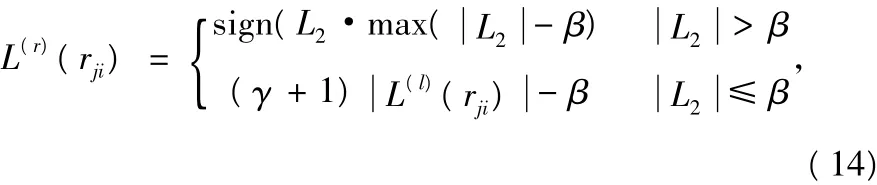
式中，γ和β的值由式(13)求得。

2 仿真实验与结果分析

在Matlab软件中，选取码长256、行重为6、列重为3、码率为1/2的规则LDPC码，经过BPSK调制后，经过高斯信道。LDPC的最大迭代次数设为50次，根据蒙特卡罗算法可以求出式(13)中的数学期望E［·］，通过仿真得到γ =0.97，β=53。根据文献［5］可知当 α =1.1时，Normalized BP-based算法具有最好的译码性能，故在改进的Min-sum算法中，令α=1.1，γ=0.97，β=53。

Min-sum算 法、NormalizedBP-based(α =1.1)、Offset BP-based(β=0.1)及改进的Min-sum算法的译码性能曲线如图2所示。从图中可以看出，对于(256，6，3)LDPC 码来说，在相同误码率BER=10－3的情况下，β =0.1的Offset BP-based算法比Min-sum算法的误码性能了约0.3 dB提高，而α=1.1的Normalized BP-based算法比Offset BP-based译码算法性大约有0.1 dB的增益，但实现复杂度稍微高些。

α=1.1，γ=0.97，β=53的改进型Min-sum算法又比α=1.1的Normalized BP-based算法的译码性能有0.1～0.2 dB的提高，相比Min-sum算法有0.5 dB的增益，其译码性能接近于LLR-BP算法。改进型的Min-sum算法的硬件复杂度相对于Normalized BP-based算法而言只增加了一个加法器，相对于Offset BP-based而言只增加了一个乘法器，因此该算法能在较低复杂度的情况下提高译码性能。LLR-BP算法虽然具有最好的译码性能，但是Min-sum算法及其改进的算法在校验节点的消息处理时采用了简化处理，提高了译码效率，其硬件实现的复杂度上要降低很多。

图2 不同译码算法的误码性能

3 结束语

该文对LDPC码常用的译码算法进行了研究，并提出一种改进型Min-sum算法，该算法的创新之处在于结合了Normalized BP-based算法和Offset BP-based的优点，并通过均方误差准则来选择参数，进一步降低了校验节点之间信息的相关性，提高了Min-Sum算法的译码性能。

［1］GALLAGER R G.Low Density Parity Check Codes［J］.IEEE Trans Information Theory，1962，8(3)：208 －220.

［2］ZHANG H T，MOURA J M F.The Design of Structured Regular LDPC Codes With Large Girth［C］∥IEEE Global Telecommunications Conference，2003(3)：4022 －4024.

［3］TIAN T，JONES C，VILLASENOR J D，et al.Construction of Irregular LDPC Codes with Low Eroor Floors［J］.IEEE Intl.Conf.Comm，2003，6：3125 －3129.

［4］TANNER R M.A Recursive Approach to Low Complexity Codes［J］.IEEE Trans.Inf.Theory，1981，27(5)：533 －547.

［5］CHEN J H，FOSSORIER M P C.Density Evolution for BP-based Decoding Algorithm of LDPC Codes and Their Quantize Versions［J］.Global Teleconference，2002，6(2)：1378 －1382.