基于声辐射控制的板结构优化设计
2012-07-31左曙光严新富李徐刚
左曙光,魏 欢,严新富,李徐刚
(同济大学 汽车学院,上海201804)
汽车乘坐室内的噪声除了小部分通过缝隙、孔洞等传入外,其余大部分都是由乘坐室周围的板件振动引起的辐射噪声[1].也就是说,车身板件的振动辐射噪声是车内最直接、最主要的噪声源.因此,对板件的辐射噪声进行控制是降低乘坐室噪声最直接有效的方法.
对薄板结构来说,一般情况下,由弯曲波所引起的横向振幅比横波和纵波大得多,因此弯曲波产生的声辐射是结构辐射噪声的主要来源[2].另外,关于声辐射模态理论的研究表明,结构声辐射效率的高低与其表面振速分布有较大的关系.在一定频率范围内,某些振速分布可以实现较小的声辐射效率,因此,优化控制结构的表面振速分布对于降低结构的辐射噪声非常有效[3].目前很多学者对结构振动的主动控制进行了大量的研究,并已取得一定的成果[4-5],怎样合理地运用声辐射模态理论来设计低辐射效率板件目前尚无成熟的理论方法.本文以工程中典型的矩形板结构为研究对象,从声辐射模态理论出发,分析讨论了影响板结构声辐射的主要因素,由此提出了优化板结构声辐射的2种方案,并对这2种方案进行了数值计算,对结果进行了简单分析.
1 板结构声辐射特性分析
根据文献[6]的研究内容可以知道,对于离散成N个微小单元的板结构来说,其在振动频率ω下的声辐射功率W(ω)可以由下式计算得到:
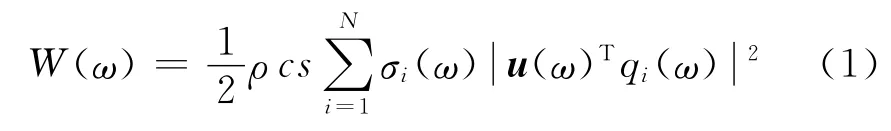
式中:ρ为介质密度,c为该处介质振动速度,ρc为声场介质的特性阻抗率;s为每个单元的面积;σi(ω)为频率ω下板结构的第i声辐射模态对应的辐射效率;N为所关心的声辐射模态总数;u(ω)指频率ω下板结构的表面振速向量;qi(ω)为频率ω下板结构的第i阶声辐射模态.若令
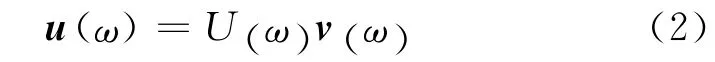
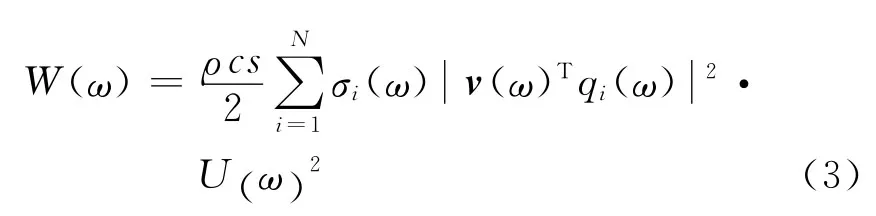
图1所示为前9阶声辐射模态对应的辐射效率特性,采用双对数坐标轴.根据参考文献[3],取量纲一化频率kl作为横坐标,其中k为波数,l为板件的长度.

图1 声辐射效率特性Fig.1 The character of radiation efficiency
声辐射效率大致具有如下特性[6]:在中低频时,各阶辐射效率差别较大,随着声辐射模态阶数的增加,辐射效率迅速减小,说明声辐射主要集中在前几阶辐射模态上.而到了高频,各阶声辐射模态的辐射效率趋于相同,声辐射由所有的模态共同贡献.
从式(3)可以看出,对于一确定的板结构,影响其声辐射功率的主要因素为表面振速振型v(ω)和振幅U(ω).其中振幅U(ω)以2次方的倍数关系影响声辐射功率,而振型v(ω)的变化则主要改变各辐射效率值的权值.
在中低频情况下,由于各阶辐射效率值差别甚大,低阶辐射效率值比高阶辐射效率值高出几个数量级.因此,可以认为振型v(ω)对声辐射的影响大于振幅U(ω)对声辐射的影响,也就是说,中低频时,板结构的振型对声辐射功率起主导作用.
而到了高频段时,所有声辐射模态的辐射效率均趋于一致.各阶声辐射模态对应的辐射效率σi(ω)随模态阶数i变化甚微,因此可以用一个固定值σ0(ω)来近似代替,式(3)变成
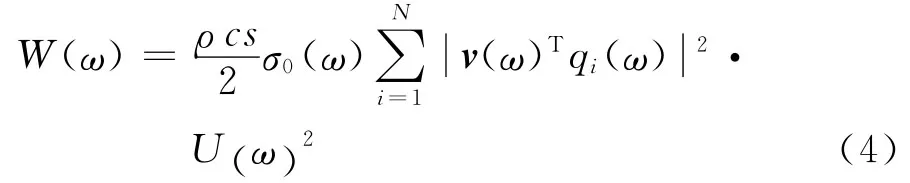
式中,σ0为各阶声辐射模态下辐射效率的平均值.又因为
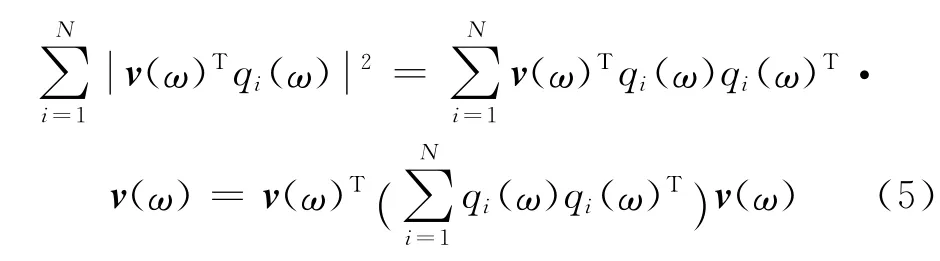
由声辐射模态的性质知qi(ω)是空间的一组单位正交基,所以有
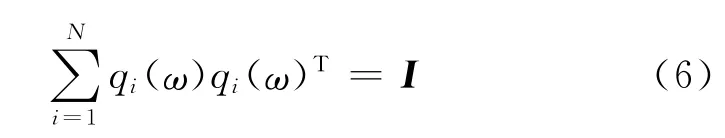
式中,I表示单位矩阵,将式(6)代入式(5)得
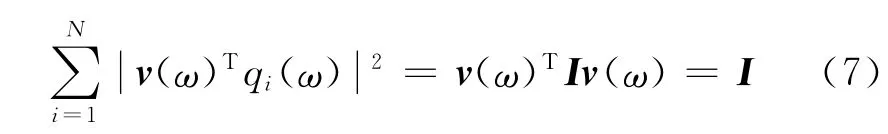
将上式代入式(4)得
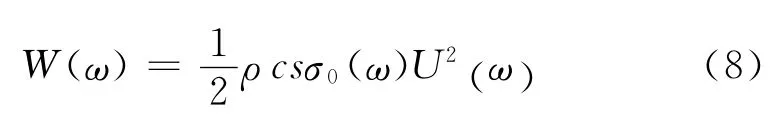
从式(8)可以知道,高频振动时,板结构辐射声功率仅与振速振幅U(ω)有关,而振型v(ω)的变化对辐射声功率基本不产生影响.
上述简单分析表明,对于板结构声辐射的优化控制需要分中低频和高频2种情况分别考虑.中低频时,总的声辐射功率不仅与振速幅值U(ω)相关,同时也和振型v(ω)相关,而振型v(ω)是主要因素,因此对结构的优化可以从控制v(ω)的角度出发;高频段时,由于总辐射效率基本保持不变,总声功率仅与振速振幅U(ω)相关,此时能有效控制声辐射的优化方法就是控制振幅U(ω)值.
2 声辐射优化方案
对于结构优化,其优化数学模型一般为
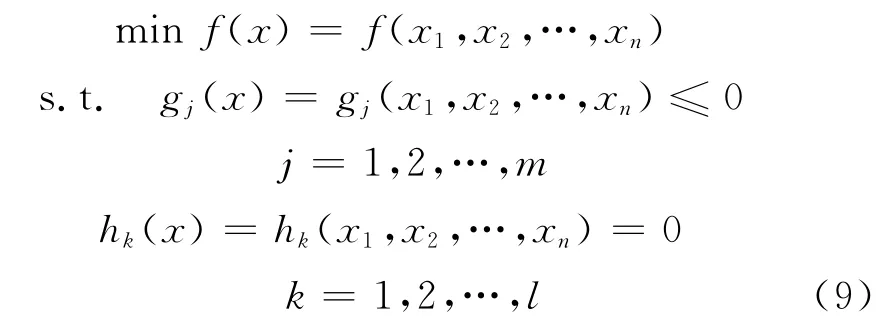
式中:f(x)为优化目标函数;gj(x)为不等式约束条件;hk(x)为等式约束条件.
如何选择优化目标函数f(x)是其中的关键步骤,优化函数的合理与否直接关系到优化结果的理想与否.前面分析表明,影响板结构的主要因素在不同频段下是不同的,因此对板结构的优化,其目标函数也要分别考虑.
在高频段时,由式(8)知道,振幅U(ω)是影响声辐射功率的唯一因素,因此优化目标函数可以取如下形式:
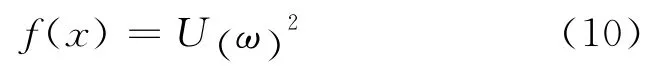
而在中低频时,虽然振型v(ω)是影响声功率的主导因素.然而,由于振型v(ω)是一个向量,并非标量,将振型v(ω)作为目标函数是不现实的.而如果以式(1)作为目标函数,计算量又太大,因此,对于中低频情况,需要作进一步分析讨论.
一些研究表明[7],中低频段时,采用形如式(1)的求和式计算板结构声功率时只需取其前6项的和便可达到较好的精度,那么此时声辐射功率计算公式可简化为
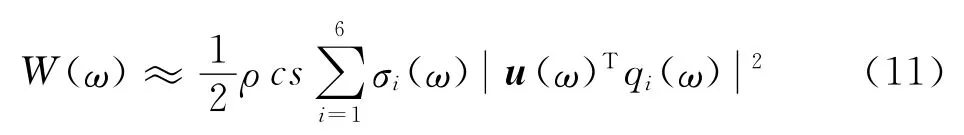
另外,中低频时各阶声辐射模态基本不随频率变化[8],因此,可以用一确定频率ω0下的声辐射模态向量qi(ω0)来代替该频段内任意频率下的声辐射模态向量qi(ω),式(11)进一步简化为

而辐射效率由于在双对数坐标中呈线性,因此可以用下式拟合:
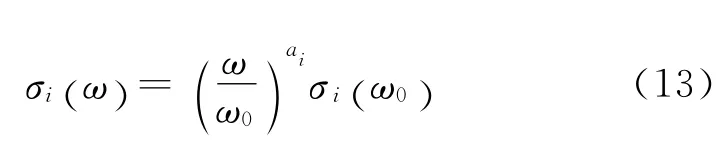
式中,ai为第i阶声辐射模态的拟合系数.
将式(13)代入式(12)中得到
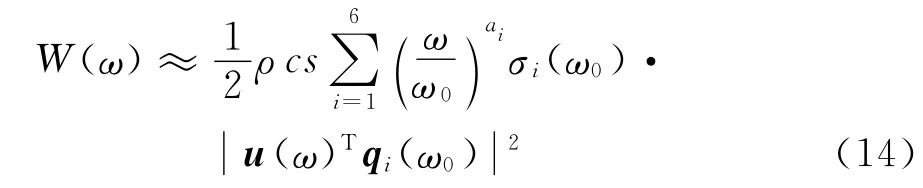
式(14)相比于式(1)来说计算量大大减少,而其计算精度仍可达到工程计算的要求.因此,可以用式(14)作为中低频段优化的目标函数,即取
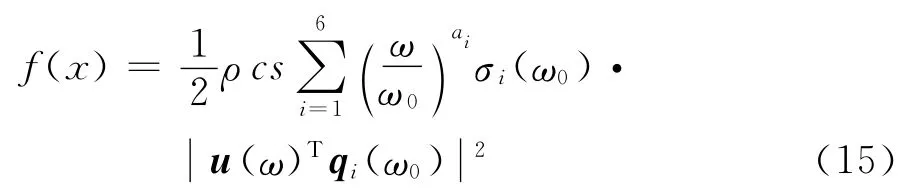
这里,由于式(15)是通过控制前6阶声辐射模态的成分来控制总声辐射功率的,即优化主要起到了改变结构振型的作用,因此称这种优化方案为“振型优化”.对应地,中高频优化的目标函数就是通过控制结构的振幅平方来减小声辐射,因此称该优化方案为“振幅优化”.
3 优化数值计算
为了验证2种优化方案的效果,采用一典型矩形板结构作为研究对象进行优化数值计算.
本计算实例采用四边固定0.6 m×0.4 m的金属板件为研究对象,在其表面施加大小为10 N·m-2的均布简谐压力.板件初始厚度为1 mm,弹性模量为E=2.1×1011Pa,密度ρ=7.9×103kg·m-3,泊松比ν=0.3.结构分成18×12个大小相等的矩形单元.声场介质为空气,密度ρA=1.21 kg·m-3,声速c=340 m·s-1.以单元厚度为变量对其进行声辐射的优化,优化目标函数分别取式(15)和式(10)的形式,从振型和振幅两方面进行优化.单元厚度值限制为0.5~2.0 mm,结构总的质量限制为不大于初始质量值.优化的频率分别取400,800,2 500,10 000及25 000 rad·s-1.优化模型采用序列二次规划法进行求解.
图2列出了各个频率下2种优化方案的优化结果.图中颜色的深浅代表了板件的厚薄,颜色越深说明优化后该处越厚,反之亦然.
对于所有的优化结果,厚度分布都呈现对称的形式,这应该主要是因为结构本身是对称的,而且边界条件和外加载荷也是对称的,所以导致优化结果是对称的.比较同一频率下2种优化方法的结果可以发现,两者之间差别较大,不同的目标函数带来了不同的优化结果.另外,同一种优化方法在不同频率下的优化结果也不相同,说明优化的结果对频率比较敏感.另外,随着振动频率的升高,优化后的厚度分布也变得越来越复杂.
图3所示为优化前后板结构声辐射功率的对比柱状图.比较2种优化方法的优化结果可以发现,在中低频段(ω≤2 500 rad·s-1),振型优化方法取得了较好的优化结果.在该频段内,振型优化前后声功率都获得了较大幅度的下降,下降量达到了30~40d B,优化效果相当明显.而在高频段(ω>2 500 rad·s-1),振型优化后声辐射功率反而比优化前更高,并且随着频率的升高,声功率上升的幅度也增加,也就是说优化起到了负面的作用.造成这种现象的主要原因还在于声辐射模态的特性,由于中低频时前几阶声辐射模态贡献了大部分的声功率,因此对前6阶声辐射模态的控制可以有效地控制声辐射功率;而到了高频时,各阶声辐射模态的辐射效率趋于相同,低阶辐射模态不再是主要的声辐射模态,而且在减小低阶辐射模态时可能导致了其他高阶辐射模态更多的增加,从而反而增加了总的声辐射.

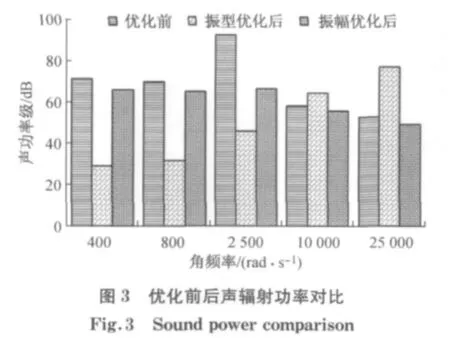
再来看振幅优化法的结果,从图中可以看出,基本上在计算的整个频段内振幅优化法都能取得一定程度的效果,然而优化幅度并没有振型优化法那么明显,大多数情况下,优化使得声功率得到了约3~5 d B的下降量.
图4是优化前后振速均方值及辐射效率的比较柱方图.比较优化前后的辐射效率值可以发现,振型优化法使得各个频段下的辐射效率都获得了不同程度的降低.特别是在中低频段,由于低阶辐射模态辐射效率远大于高阶辐射模态,因此对低阶辐射模态的消除同时也大幅降低了结构的总辐射效率.这时,虽然结构的振速均方值没有降低,但是仍能较大幅度地降低声辐射功率.而到了高频段,振型优化前后的辐射效率变化不大,而此时由于结构改变反而造成了振速均方值较大幅度地增加,所以声辐射功率亦随之增加.
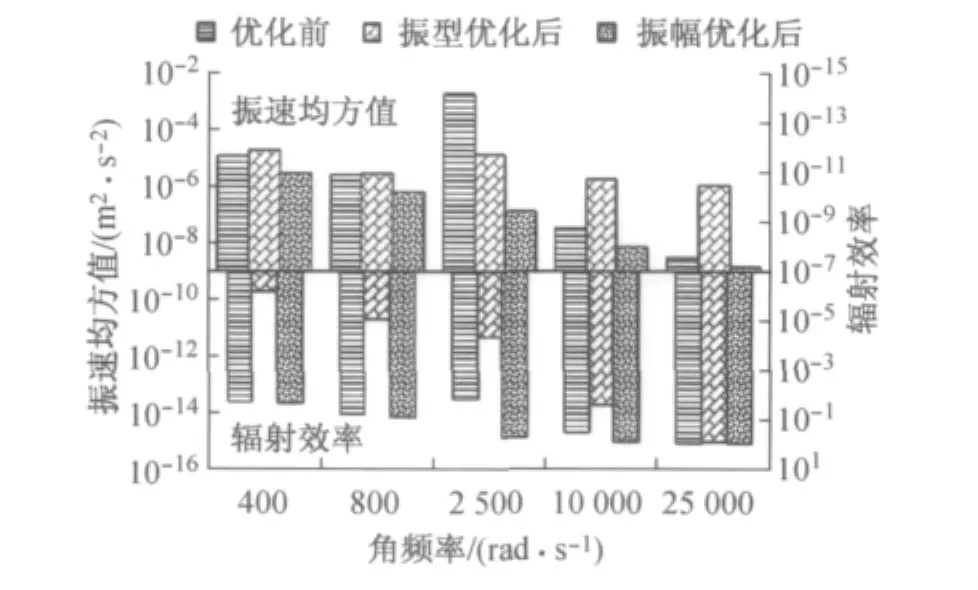
图4 振幅均方值及辐射效率对比Fig.4 Comparison of U 2 andσ
由于振幅优化法的目标函数就是振速均方值,因此振幅优化后各个频率的振速均方值都获得了不同程度的下降.振幅优化法对辐射效率的影响不大.
上述分析可以大致得出这样一个结论:振型优化法主要改变的是结构的声辐射效率,中低频对振速均方值的影响不大,适用于中低频段的优化;而振幅优化法主要改变的是结构的振速均方值,在整个频段均能获得一定程度的优化效果,在高频段优化比较有优势.
4 结论
主要以声辐射模态理论为基础,对板结构的声辐射特性进行了分析研究,由此提出了振型优化和振幅优化这2种优化方案,并使用这2种方案对一典型矩形板进行了优化设计的数值计算.结论主要是基于声辐射模态理论得出的,而结构的声辐射模态只与其形状和大小有关,与其他特性(如材料等)并无直接关系,因此平板的初始振动模态对本文结果没有直接影响,仿真所用的平板固有振动频率不影响结论的普适性.研究主要结论如下:
(1)板结构的振型对中低频声辐射起主导作用,振动幅值的大小亦在一定程度上对声辐射产生影响.
(2)高频振动时,板结构的振型分布基本不影响声辐射,振动幅值大小决定了声辐射功率的大小.
(3)振型优化在中低频段效果明显,高频段可能适得其反,因此仅适用于中低频段.
(4)振幅优化可在整个频段取得一定的优化效果,在中低频段的作用不如振型优化法,可适用于高频段的声辐射优化.
[1] 靳晓雄,张立军.汽车噪声的预测与控制[M].上海:同济大学出版社,2004.JIN Xiaoxiong,ZHANG Lijun.Prediction and optimization of the vehicle noise [M]. Shanghai: Tongji University Press 2004.
[2] 何琳,朱海潮,邱小军,等.声学理论与工程应用[M].北京:科学出版社,2006.HE Lin,ZHU Haichao,QIU Xiaojun,et al.Acoustic theory and engineering application[M].Beijing:Science Press,2006.
[3] 毛崎波,姜哲.对声辐射模态的讨论[J].振动工程学报,2000,13(4):633.MAO Qibo,JIANG Zhe.Discuss on sound radiation modes[J].Journal of Vibration Engineering,2000,13(4):633.
[4] 周晓楠,姜哲,吴苏萍.基于时域声辐射模态的结构噪声主动控制研究[J].振动与冲击,2006,25(6):29.ZHOU Xiaonan,JIANG Zhe,WU Suping.Active control research of structure noise based on time domain acoustic radiation modes[J].Journal of Vibration and Shock,2006,25(6):29.
[5] 李双,陈克安,潘浩然.基于模态理论的有源声学结构控制机理研究[J].振动工程学报,2007,20(2):140.LI Shuang,CHEN Kean,PAN Haoran.Control mechanism research of active acoustic structure based on model theory[J].Journal of Vibration Engineering,2007,20(2):140.
[6] 毛崎波,姜哲.通过声辐射模态研究结构噪声的有源控制[J].江苏理工大学学报,2000,21(4):1.MAO Qibo,JIANG Zhe.Structure noise’s active control on the acoustic radiation modal[J].Journal of Jiangsu Polytechnic University,2000,21(4):1 .
[7] 姜哲.基于声辐射模态确定声功率[J].江苏大学学报,2005,26(6):537.JIANG Zhe.Ensure the sound power based on the acoustic radiation modal[J].Journal of Jiangsu University,2005,26(6):537.
[8] 毛崎波,徐柏龄,姜哲.对声辐射模态的改进[J].振动工程学报,2002,15(3):262.MAO Qibo,XU Boling,JIANG Zhe.The improvement on acoustic radiation modal[J].Journal of Vibration Engineering,2002,15(3):262.
