支持动态重构的制造系统逻辑控制器设计方法

谢 楠，李爱平

（1.同济大学 中德工程学院，上海201804；2.同济大学 机械工程学院，上海201804）

随着全球化、动态化和用户驱动为显著特征的市场竞争的加剧，制造业不仅面临着技术进步带来的机遇，同时还面临着快速多变和难以预测的市场环境，使得制造企业的生产方式已由面向产品的生产转变为面向顾客的生产.因此，迫切需要发展一种能够通过制造资源构件调整和生产系统快速重构，适应生产系统内、外部各种影响因素快速变化的制造系统[1－3].

为了适应上述特点，支持资源快速重构的制造系统逻辑控制器必须满足以下条件：① 支持不同组元之间逻辑控制关系的改变、更新；② 短的逻辑控制器重构斜升时间；③ 适应不同产品的混流生产；④ 重构后的逻辑控制器可形式化地验证其性能.

文献[4]介绍了采用Petri网对制造系统进行建模以及防死锁方法.文献[5]针对柔性制造系统（flexible manufacturing system，FMS）的制造单元采用网合成技术进行了建模并分析可逆、有界、活性等行为特性.在逻辑控制器设计领域，针对制造系统可重构这一特点，文献[6－7]采用基于信号解释Petri网的控制器设计和分析方法，利用模块化方法进行控制器设计，采用可达图和化简技术相结合，分析了逻辑控制器的重构能力.文献[8]提出了通过变量调整可快速重构逻辑控制器的方法，并证明了控制器的活性、安全和可逆.文献[9－10]提出基于事件的制造系统逻辑控制器设计，并进行控制器行为特性分析.上述这些方法在逻辑控制器的重构设计方面取得诸多成果，但方法较为复杂并且对应用场景做了特定限制，不易应用于工业现场.

近年来，Llorens等[11－12]提出了网重写系统以及可重构Petri网，为制造系统的逻辑控制器设计提供了新的思路.

本文针对制造系统中生产资料的重构变化，研究基于可重构Petri网的制造系统逻辑控制器设计方法，建立重写规则，分析逻辑控制器的行为特性.当制造系统的被加工零件改变后，控制器可快速改变自身控制逻辑形成新的逻辑控制器以适应新的生产构型.

1 支持动态重构的制造系统逻辑控制器

定义1 支持动态重构的制造系统逻辑控制器是基于可重构Petri网的制造系统控制逻辑形式化模型，它由控制逻辑和重构规则组成，可以动态改变自身结构适应不同的逻辑控制功能.

1.1 网重写系统和可重构Petri网

1.1.1 网重写系统

Llorens等[11]提出网重写系统对动态系统进行建模，系统的构型是某一具体Petri网描述而其变化则由网重写规则给出.

定义2[11]网重写系统为一结构N＝（R，（Γ0，M0）），其中R＝ ｛r1，r2，…，rh｝是一个有限网重写规则集，（Γ0，M0）是一个标识Petri网可用来表示一个制造系统的构型C.

一条重写规则r∈R是一个结构r＝（L，R，τ·，τ，τ·），其中：

（1）L＝（PL，TL，FL）和R＝（PR，TR，FR）是Petri网，分别称之为左手侧和右手侧.

（2）r⊆（PL×PR）∪（TL×TR），称为r的传递关系，是一个表示从库所L到库所R以及变迁L到变迁R的二元关系：PLτ⊆PR，τPR⊆PL，TLτ⊆TR以及τTR⊆TL.

1.1.2 可重构Petri网

可重构Petri网是一类特殊的网重写系统，定义如下：

定义3[11]可重构Petri网N＝（P，T，R，γ0），其中，P＝ ｛p1，p2，…，pn｝是非空的库所有限集合，T＝ ｛t1，t2，…，tm｝是 非 空 的 变 迁 有 限 集 合，P（P∩T）＝Φ，R＝ ｛r1，r2，…，rh｝是 有 限 重写规则的集合，γ0是初始状态.

定义4[11]可重构Petri网N＝（P，T，R，γ0）的构型图G（N）是一个有向图，图的节点表示了系统的配置，从构型Γ到构型Γ′由弧r＝（D，）∈R标识，记为Γ [r＞Γ′（p，t）（t，p）分别表示输入和输出接口关系，当且仅当：

定理1[11]任何一个可重构Petri网都等价于某个普通Petri网.

1.2 逻辑控制器及其重构机制

随着制造系统组元升级和组态更新，逻辑控制器根据生产任务、车间调度以及制造系统的新构型，快速生成新的逻辑控制器，其具体结构及重构机制如图1所示.

2 逻辑控制器的设计方法

逻辑控制器的设计要根据制造系统的设备进行被控设备的控制建模、定义重写规则、确定过渡连接、分析控制器行为特征、确定控制逻辑.

2.1 设备子网建模

（1）加工设备控制模块 指完成特定工序要求的加工设备控制模型，其Petri网的表达模块如图2所示.图2中P1为加工设备启用并准备开始加工，P2为加工设备处于空闲状态，T1为原材料达到加工设备缓冲，T2为加工设备加工零件.

（2）机器人控制模块 指完成物料搬运动作的搬运机器人控制模型，其Petri网的表达模块如图3所示.P1为机器人处于工作加工，P2为机器人到达目的地，P3为机器人处于空闲状态，T1为零件达到机器人搬运起点，T2为零件离开机器人搬运终点，T3为机器人回到运动起点.

图1 逻辑控制器及其重构机制Fig.1 Logic controller and its reconfiguration mechanism

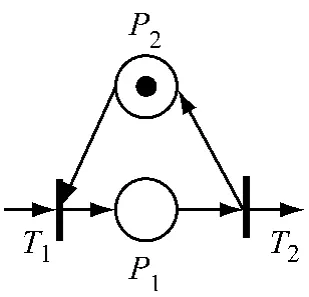
图2 加工设备Petri网控制模块Fig.2 Petri control module of machine

图3 机器人Petri网控制模块Fig.3 Controlling module of Petri Nets of Robot

2.2 重写规则定义

制造系统的重构主要包括了物理重构和逻辑重构.物理重构主要表现为设备的增加和移除、设备自身结构的变化；逻辑重构主要表现为设备之间联系的变化，如工序前后次序的变化、缓冲区位置的变化.

（1）逆向

物流子系统是制造系统的主要部分，物流路线也一定程度决定了生产过程.不同的零件以及不同的加工工艺都会带来物流路线的改变，这种情况定义为逆向的重写规则，如图4所示，图中A为完成特定功能的一类变迁，P为完成特定功能的一类库所.

图4所对应的重写规则采用形式和表示法描述如下：P（－A）＋P（A）▷P（A）＋P（－A）.

（2）多到单／单到多（移走／增加设备）

系统构型中有工序要增加加工设备，以增强该工序的加工能力；或者工序减少加工设备，降低工序的加工能力，这种情况定义为多到单／单到多的重写规则，如图5所示，其中图中A、B为完成特定功能的一类变迁，P、Q、S为完成特定功能的一类库所.

图4 逆向重写规则Fig.4 Reverse reconfiguration rules

图5 多到单／单到多重写规则Fig.5 Multi－to－single／single－to－multi reconfiguration rules

图5所对应的重写规则采用形式和表示法描述如下：P（－A－B）＋Q（－A＋A）＋Q（A－A）＋S（－B＋B）＋S（B－B）＋P（A＋B）▷P（－A）＋Q（－A＋A）＋Q（A－A）S（－B＋B）＋S（B－B）＋P（A）.

（3）串到并／并到串

系统构型中有工序之间的逻辑联系要改变，如从原来的串行改成并行加工方式，以改变系统的加工能力或功能，这种情况定义为串到并／并到串的重写规则，如图6所示，其中图中A，B为完成特定功能的一类变迁，P，Q，S为完成特定功能的一类库所.

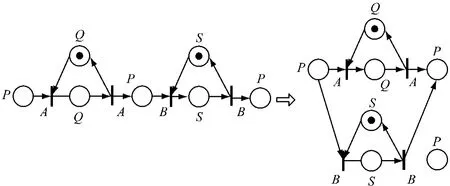
图6 串到并／并到串重写规则Fig.6 Seria to parallel／parallel to serial rules

图6所对应的重写规则采用形式和表示法描述如下：

P（－A）＋Q（－A＋A）＋Q（A－A）＋P（A－B）＋S（－B＋B）＋S（B－B）＋P（B）▷P（－A－B）＋Q（－A＋A）Q（A－A）＋S（－B＋B）＋S（B－B）＋P（A＋B）.

上述重写规则反向亦成立.

2.3 根据重写规则重构逻辑控制器

当制造系统发生重构后，将上述重写规则根据实际系统物理和逻辑重构变化应用到过渡连接，构建新的逻辑控制器.基于可重构Petri网的逻辑控制器重构后其性能是可判定，通过行为特性分析验证其可逆、有界和活性等性能.

3 实例分析

本论文以一条箱体类零件生产线的实际生产过程为研究对象，进行逻辑控制器的设计和重构.该生产线可生产箱体类零件的若干系列，生产线的3种不同配置分别适应不同系列零件的混流生产，分别称为配置X，配置Y以及配置Z.生产线共4台加工设备并组成三道工序，生产线呈流水线布局，其中有一个运输机器人进行物料输送.

该生产线的重构方式主要包括：① 工序三增减加工设备，可改变生产能力和生产节拍.② 工序一和工序二改变加工设备间的物流联系，串改并或者并改串.该生产线可根据不同产品系列的转产需要，快速改变生产系统的构型，实现产品的快速转产.

3.1 支持重构的逻辑控制器建模

（1）构建逻辑控制器 生产线在配置X的构型下所生产的零件数量较多，为生产线主配置方案.根据第2节提出的逻辑控制器设计方法，其逻辑控制器的Petri模型如图7所示.图中的各个符号含义表示：P0为原材料在第一台设备等待，P1为第一台设备正在加工，P2为第一台加工设备空闲，P3为第一台设备加工后缓冲空闲，P4为第二台设备正在加工，P5为第二台加工设备空闲，P6为第二台设备加工后缓冲空闲，P7为机器人空闲，P8为机器人正在工作，P9为机器人等待回到起始位置，P10为第三台设备正在加工，P11为第三台加工设备空闲，P12为第四台设备正在加工，P13为第四台加工设备空闲，T0为被加工件进入第一台设备，T1为第一台设备加工完毕进入缓冲，T2为被加工件进入第二台设备，T3为第二台设备加工完毕进入缓冲，T4为机器人从缓冲拿走被加工件，T5为机器人将被加工件放入第三台设备，T6为机器人正在复位，T7为被加工件在第三台设备加工完毕，T8为被加工件放入第四台设备，T9为被加工件在第四台设备加工完毕（变迁和库所含义下同）.

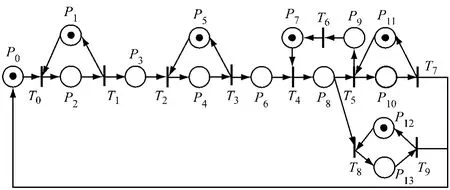
图7 生产系统配置X的Petri网模型Fig.7 Petri nets model of configuration X of production system

图7模型对应的配置X方案中，加工设备1和加工设备2串行连接形成工序一和工序二，加工设备3和4并联形成工序三.

（2）重构逻辑控制器 当被加工零件发生变化时，生产线的构型需要随之快速动态调整，并生成新的系统逻辑控制器.

① 重构方式一：当被加工零件型号改变，零件的形位精度提高后，为了保证被加工件的位置度精度，将图7中第一道工序和第二道工序由串行重构为并行，采用工序集中方式，一次装夹后将相关的孔和面加工完成.同时，工序三的节拍变短，不再需要设备3和设备4并行完成工序三.这种情况下，随着加工工艺的改变生产线的构型也相应重构到配置Y，重构后的系统逻辑控制器如图8所示.

图8 生产系统配置Y的Petri网模型Fig.8 Petri nets model of configuration Y of production system

② 重构方式二：由于加工工艺的差别，不同系列的被加工零件生产节拍发生变化，会导致瓶颈工位的变化.在实际箱体类零件生产过程，某些系列产品在工序三的节拍变快，因此，移除不必要的加工设备以平衡生产节拍，即重构成了配置Z方式.重构后的系统逻辑控制器如图9所示，变迁和库所含义同图7.

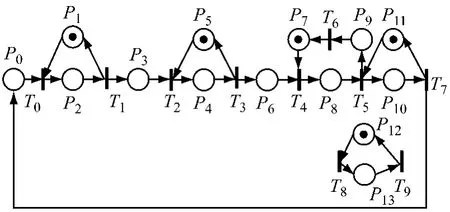
图9 生产系统配置Z的Petri网模型Fig.9 Petri nets model of configuration Z of production system

3.2 逻辑控制器行为特性分析

分析X、Y和Z逻辑控制器模型的可达图可知：三个控制器都是有界、安全和无死锁的.因此制造系统在构型发生变化，利用重写规则快速重构逻辑控制器，重构后的逻辑控制器仍然保持了良好的行为特征，可用于制造系统的控制.

4 结论

（1）采用可重构Petri网对制造基本单元以及系统的控制给出形式化定义并进行建模，建立了系统重写规则.

（2）提出了制造系统逻辑控制器设计方法，根据制造系统构型的变化，通过重写规则快速重构成新的逻辑控制器.

（3）以一个实例详细阐明了支持动态重构的制造系统逻辑控制器设计过程，并给出了重构方法.其结果证明，提出的逻辑控制器具有快速重构能力并保持了系统的行为特性，验证了方法的有效性.

采用本文提出的制造系统逻辑控制器设计方法可应用在任意离散事件动态系统的控制器建模，特别适用于通过资源重构以适应不同零件加工的生产方式.但是，目前这种逻辑控制器建模方式仅仅限于系统层而不能对设备层进行建模；此外，网重写规则限于资源增加、减少以及联系变化等有限的重写模式.因此，如何针对设备层进行控制器建模以及增加更多的重写规则是进一步需要研究的内容.

[1] Mehrabi M G，Ulsoy A G，Koren Y，et al.Trends and perspectives in flexible and recon
Figurable manufacturing systems[J].Journal of Intelligent Manufacturing，2002，13（2）：135.

[2] 梁福军，宁汝新.可重构制造系统理论研究[J].机械工程学报，2003，39（6）：36.LIANG Fujun， NING Ruxin. Theoretical research of recon
Figurable manufacturing system[J].Chinese Journal of Mechanical Engieering，2003，39（6）：36.

[3] XIE Nan，LI Aiping.Recon
Figurable production line modeling and scheduling using Petri nets and genetic algorithm[J].Chinese Journal of Mechanical Engineering，2006，19（3）：362.

[4] LI Zhiwu， ZHOU Mengchu， WU Naiqi. A survey and comparison of petri net－based deadlock prevention policies for flexible manufacturing systems[J].IEEE Trans On Systems，Man and Cybernetics，2008，38（2）：173.

[5] Pouyan Ali A，Shandiz Heydar Toossian，Arastehfar Soheil.Synthesis a Petri net based control model for a FMS cell[J].Computers in Industry，2011，62（5）：501.

[6] 李俊，戴先中，孟正大.基于信号解释Petri网的可重构逻辑控制器分析和设计[J].东南大学学报，2004，34（11）：101.LI Jun，DAI Xianzhong，MENG Zhengda.Analysis and design of recon
Figurable logic controllers based on signal interpreted Petri nets[J].Journal of Southeast University，2004.34（11）：101.

[7] 李俊，戴先中，孟正大.可重构制造系统监督控制器的自动重构[J].自动化学报，2008，34（11）：1337.LI Jun， DAI Xianzhong， MENG Zhengda. Automatic reconfiguration of supervisory controllers for recon
Figurable manufacturing systems[J].ACTA Automatica Sinica，2008，34（11）：1337.

[8] 谢楠，李爱平，尤建新，等.支持混流生产的可重组逻辑控制设计方法[J].计算机集成制造系统，2008，14（5）：842.XIE Nan，LI Aiping，YOU Jianxin，et al.Design methodology of recon
Figurable logic controller for hybrid production[J].Computer Integrated Manufacturing Systems，2008，14（5）：842.

[9] Part E，Tilbury D M，Khargonekar P P.A modeling and analysis methodology for modular logic controllers of machining systems using Petri net formalism[J].IEEE Transactions on Systems，Man and Cybernetics，2001，31（2）：168.

[10] Park E，Tilbury D M，Khargonekar P P.Modular logic cotrollers for machining systems：Formal representation and performance analysis using Petri nets[J].IEEE Trans On Robotics and Automation，1999，15（6）：1046.

[11] Llorens M，Oliver J.Structural and dynamic changes in concurrent systems：recon
Figurable Petri nets[J].IEEE Transactions on Computers，2004，53（9）：1147.

[12] Badouel E， Llorens M， Oliver J. Modeling concurrent systems：recon
Figurable nets[C]／／Proceeding International Conference on Parallel and Distributed Processing Techniques and Applications.Las Vegas：CSREA Press，2003：1568－1574.