软黏土的三轴蠕变试验与修正的Singh-Mitchell蠕变模型
2012-07-31刘业科邓志斌曹平黄永恒林杭
刘业科,邓志斌,曹平,黄永恒,林杭
(1. 中南大学 资源与安全工程学院,湖南 长沙,410083;2. 湖南省公路管理局,湖南 长沙,410011)
土体蠕变特性的早期研究一般都集中在其本构模型的建立和一些非常理想化问题的解析解,研究成果能够直接应用于生产实际的并不多[1-3]。随着数值解的发展,土流变理论的工程应用取得了长足发展,选用适当的本构模型和求解方法,解决实际工程中出现的各类问题,已成为土流变研究的重要发展方向和发展趋势[4-7],于是,发展了非线性经验蠕变模型,即完全通过室内试验结果而抽象的应力-应变-时间关系。对于不同的土、不同的试验条件,可能有各不相同的经验公式。虽然这样建立的经验模型缺乏严密的理论依据,仅能反映简单加载或特定应力路径情况下的蠕变现象,但是,经验模型的优势在于只要少量的参数就
能达到较好的拟合效果,所以,在工程实践中具有一定的应用价值。早期的土体蠕变试验主要为最为方便的利用常规固结仪的一维固结试验,但其试验加载路径为特殊的等有效应力比路径,使得土样在该试验条件下蠕变得不到充分发挥,蠕变速率随蠕变程度的增加而减小。为了充分揭示土体蠕变特性和规律,可选择进行三轴固结蠕变试验,如著名的经验蠕变模型Singh-Mitchell模型[8]与Mesri模型[9]就是总结三轴蠕变试验结果的基础上提出的。此后国内外不少研究者在采用三轴固结蠕变试验的基础上,针对这2种著名的经验蠕变模型开展了土体蠕变特性的研究。Lin等[10]比较了Singh-Mitchell模型与Mesri模型的不同之处,提出了考虑超固结因素的新的蠕变方程,此方程拓展了偏应力水平D的适用范围。王常明等[11]探讨了滨海软土的三轴蠕变规律,针对试验结果研究得到软土具有非线性蠕变特性,将 Singh-Mitchell蠕变模型中的应力-应变关系修正为双曲线是合适的,并建立了相应的蠕变模型。王琛等[12-15]分别采用Singh-Mitchell模型与Mesri模型描述三峡泄滩滑坡滑动带土的蠕变特性,并提出了改进的Mesri模型,即对其应变-时间幂函数关系中的幂指数依据蠕变的不同阶段(蠕变衰减、等速蠕变和稳定蠕变)进行分段拟合。卢萍珍等[16]在总结 Singh-Mitchell模型与 Mesri模型的基础上,提出了采用幂函数表示应力-应变关系,采用双曲线表示应变-时间关系的蠕变方程。这些学者对软黏土经验蠕变模型选取何种函数体来模拟蠕变试验的应力-应变关系和应变-时间关系的分析不够深入,有必要开展进一步的研究工作。在此,本文作者以湖南省竹城公路路基软黏土为研究对象,开展三轴蠕变试验,首先采用 Singh-Mitchell蠕变模型对该软黏土蠕变特征进行描述,分析其计算结果与室内试验结果的差异的原因,并对 Singh-Mitchell蠕变模型提出了相应的修正方法。
1 三轴蠕变试验
1.1 试验仪器及土样基本物理力学指标
试验仪器为中科院武汉岩土所对普通的 SJ-1A.J型应变式三轴仪改装而成新三轴蠕变试验仪。
土样取自湖南省竹城公路某高路堤路段,取样深度为 3.6~8.0 m。针对土样开展了一系列室内土工试验,取得该土样的基本物理力学性质指标如下:天然含水率为42.3%,湿密度为1.79 g/cm3,土中固体矿物的质量与同体积4 ℃时的纯水质量比为2.71,液限为41.9%,塑限为20.1%,平均孔隙比为1.19,压缩系数为0.64 MPa-1,压缩模量为3.07 MPa,黏聚力为6.6 kPa,内摩擦角为21°,可知该土样为软塑黏土[17]。
1.2 加载方法与步骤
土体的室内蠕变试验通常有恒定荷载和梯级荷载2种加载方法。本文的室内蠕变试验采用梯级荷载加载方法。试验步骤如下:首先,进行室内CU三轴剪切试验,以确定不同围压下的破坏偏应力qf,这里的qf为一定围压 σ3下达到破坏时的轴压 σ1与围压 σ3差值,为确定蠕变试验梯级荷载加载等级提供依据。其次,根据土样的破坏偏应力qf,确定蠕变试验的各级荷载(加载等级n一般分为5~8个等级,即n=5~8,每级应力水平增量为(qf/n))。从所设定的第一个应力等级水平开始进行分级加载三轴蠕变试验,根据参考文献[18],认为三轴固结不排水蠕变试验的每级的蠕变稳定标准为连续1 d内变形量小于0.01 mm即视为达到稳定状态,则可以进入拟定的下一级应力水平蠕变试验。蠕变试验试样直径Φ=39.1 mm,高度H=80 mm。整个蠕变试验都在控制温度为(24±1) ℃范围内进行,以保证外界温度对试验的影响最小化。
1.3 试验结果
以围压σ3为100 kPa的土样为例进行试验并对试验结果进行分析。通过对土样进行三轴固结不排水试验(CU试验),确定土样围压σ3为100 kPa时的破坏偏应力qf为134 kPa,见文献[17]。根据CU试验结果确定三轴固结不排水蠕变试验为6级加载,各级偏应力q1~q6依次为 30,60,90,110,140 和 170 kPa。根据确定的6级偏应力进行三轴蠕变试验,可得100 kPa围压下土样的三轴蠕变全过程试验曲线、由梯级荷载加载转换所得的恒定荷载加载试验曲线和蠕变等时曲线,见图1~3。

图1 100 kPa围压下三轴蠕变全过程试验曲线Fig.1 Full-process tri-axial creep curve under confining pressure of 100 kPa
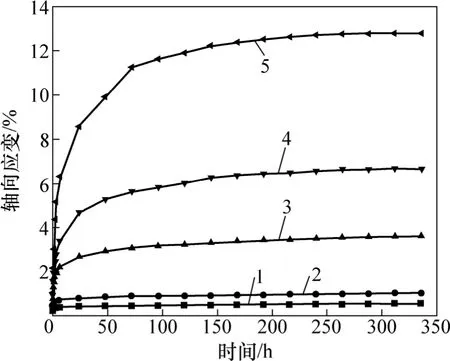
图2 100 kPa围压下土样的恒定荷载加载蠕变曲线Fig.2 Creep curves under different single load levels with confining pressure of 100 kPa

图3 100 kPa围压下土样的应力-应变等时曲线Fig.3 Stress-strain isochronal curves under confining pressure of 100 kPa
从图1~3可以看出,土样在试验过程中表现出明显的非线性变形特征。由图1和图2可知:当所施加的偏应力q(如q=30,60,90,110,140 kPa)低于一定值时,应变-时间曲线具有明显的衰减特征,在加载初期应变量快速增长;随着试验时间延长,应变量减速增大并最终趋近于极限应变量值ε∞,土样未发生破坏;而当所施加的偏应力(如q=170 kPa)高于这一数值时,应变量将加速增大并最终导致土样破坏。分析试验结果后可初步判断土样的破坏偏应力在 140~170 kPa之间,从保守的角度考虑,可将围压为 100 kPa下土样的破坏偏应力qf修正为150 kPa。由图3可知:试验时间相等的前提下,应力-应变曲线具有明显上扬的特征,应变总量随所施加偏应力的增大而加速增长,不同应力下土样的瞬时应变量较小且变化不大。所得到的三轴梯级荷载加载蠕变试验数据、曲线和结果分析及修正后的土样破坏偏应力qf为经验蠕变模型的建立与验证提供了依据。
2 经验蠕变模型
2.1 岩土体经验蠕变模型简介
岩土体的非线性经验蠕变模型表现为完全通过室内蠕变试验结果而抽象得到的应力-应变-时间关系,其蠕变方程包括变形函数(应力-应变关系)和蠕变函数(应变-时间关系)2部分。其中,应力-应变关系可由幂函数、指数函数和双曲线函数表示,应力-时间关系可由幂函数、对数函数、指数函数和双曲线函数表示[19]。在建立蠕变方程时,既可选择相同的函数来表达应力-应变关系和应变-时间关系,也可选择不同函数形式进行组合,究竟选择何种函数组合形式由应力-应变试验曲线和应变-时间试验曲线满足何种形式的函数关系而定。
2.2 Singh-Mitchell经验蠕变模型
1968年 Singh等[8]提出的著名的 Singh-Mitchell经验蠕变模型是在总结了单级常应力加载,排水与不排水三轴压缩试验数据的基础上,采用指数函数表示应力-应变关系、采用幂函数表示应变-时间关系的经典的经验蠕变模型,该模型能够很好地反映土的蠕变特性。此外,国内一些专家学者也采用该模型对一些地区的软黏土蠕变特征进行描述,认为该模型可以很好地模拟一些地区软黏土的蠕变特性[11-12]。因此,本文首先采用原 Singh-Mitchell经验蠕变模型模拟软黏土的蠕变特性,探讨该模型计算结果与室内蠕变试验结果的差异,以针对其不足提出相应的修正方法。Singh-Mitchell经验蠕变模型方程可表示为:
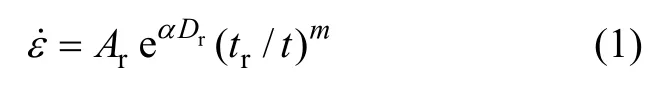
对式(1)进行积分,m≠1且不考虑初始应变,可得:

式中:B=Artr/(1-m);β=a;λ=1-m。
当t=tr时,式(2)可以写成:
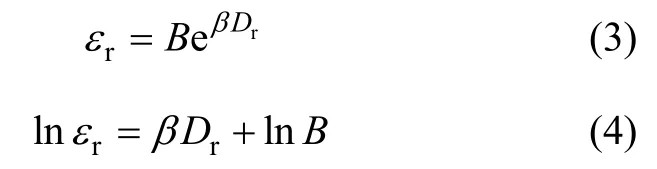
根据式(3)和式(4),β和 B的可以直接从 tr=1 h时的lnεr-Dr关系曲线图中的斜率与截矩求得。
由式(2)~(4)可知:Singh-Mitchell经验蠕变模型只需要确定的3个参数为B,β和λ。
首先确定λ。根据三轴蠕变试验结果(详见参考文献[17]),将图2的坐标进行对数变化即可绘制出蠕变lnε-lnt关系曲线,对lnε-lnt曲线进行线性拟合后的斜率λ平均值为0.171 5。
然后确定B和β。根据CU试验和三轴蠕变试验结果,将围压为100 kPa下土样的破坏偏应力qf修正为150 kPa,则各级偏应力下的应力等级如表1所示。

表1 梯级加载下的偏应力水平Table 1 Deviatoric stress level under multi-grade load
取 tr=1 h,lnεr-Dr关系曲线见图 4,对 lnεr-Dr曲线进行线性拟合后的斜率 β与截矩 lnB分别为:β=3.081 2,lnB=-6.246 3,则 B=0.001 9。

图4 围压为100 kPa的土样的lnεr-Dr关系曲线Fig.4 Relationship of lnεr-Dr for soil sample with surrounding stress of 100 kPa
则围压 100 kPa下三轴蠕变试验软黏土的Singh-Mitchell蠕变方程的表达式为:
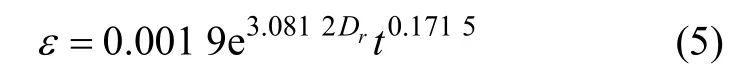
取一定的时间变量,根据三轴蠕变试验结果和式(5)的计算结果可得出tr=1 h后的Singh-Mitchell蠕变模型计算曲线与试验曲线的比较图(见图5)。
由图5可知:软黏土的Singh-Mitchell蠕变模型计算曲线与室内三轴蠕变试验曲线基本趋势一致,都是在加载初期应变快速增长,随着加载时间的增加,应变表现出明显的衰减特征;但是,在各偏应力下传统的 Singh-Mitchell蠕变模型计算结果与实验结果的误差较大,Singh-Mitchell蠕变模型描述偏应力在破坏偏应力的20%~80%范围内的蠕变行为较为合适,如当偏应力Dr=0时,实际的εr应为0,而 Singh-Mitchell蠕变模型计算结果仍有极限长期应变 0.001 9;当Dr=0.933 3时,Singh-Mitchell蠕变模型计算的蠕变量远小于实验结果,并且各偏应力下的模型计算曲线在蠕变后期上升较快,曲线较陡,偏离试验曲线。由上分析可知:传统的 Singh-Mitchell经验蠕变模型的计算结果与软黏土三轴蠕变试验结果吻合度不高,需要对该模型进行修正。
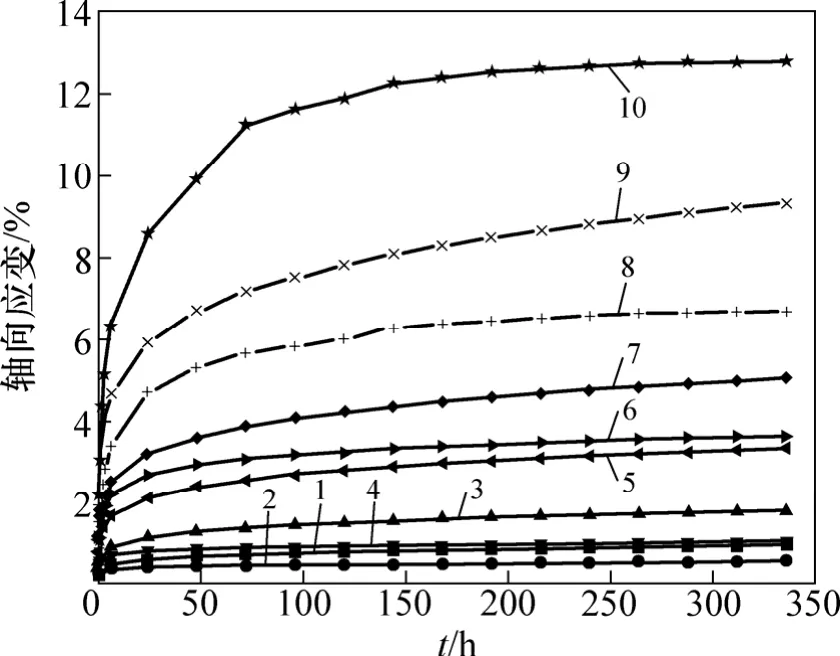
图5 试验曲线与Singh-Mitchell模型计算曲线比较图Fig.5 Comparison of results obtained from Singh-Mitchell model and laboratory tests
2.3 修正的Singh-Mitchell经验蠕变模型
传统的 Singh-Mitchell经验蠕变模型对软黏土蠕变试验结果的拟合不好,需要对模型进行修正。由于岩土体的非线性经验蠕变模型表现为完全通过室内蠕变试验结果而抽象得到的应力-应变-时间关系,因此其蠕变方程究竟选择何种函数组合形式由应力-应变试验曲线和应变-时间试验曲线满足何种形式的函数关系而定。从图2、图3和传统的Singh-Mitchell经验蠕变模型蠕变方程的分析结果可知,导致该模型蠕变方程的计算结果与试验蠕变结果出现误差的主要有 2个原因。
(1) 分析图3试验应力-应变等时曲线可知:该软黏土土样的应变随所施加偏应力的增大而加速增大,同时具有凹函数曲线和单调增加函数曲线的特征,所以经验蠕变模型方程中用于描述试验应力-应变关系的函数必须同时具备这 2个特征。由于传统的Singh-Mitchell经验蠕变模型采用指数函数描述应力-应变关系,因此,对指数函数进行最小二乘法拟合分析,结果表明指数函数可以同时满足凹函数和单调增加函数的特征,则可确定采用指数函数描述软黏土三轴蠕变试验的应力-应变关系是合适的。但是,传统的 Singh-Mitchell经验蠕变模型采用指数函数描述应力-应变关系时,由于采用单纯的自然指数形式εr=BeβDr,致使当 Dr=0 时,εr=B 不为 0,与实际不符。
(2) 分析图2试验应变-时间曲线可以可知:该软黏土土样衰减蠕变阶段的应变量随试验时间的增长而减速增大并最终趋于一极限值,具有明显的衰减特征,同时满足有极值、凸函数曲线特征和单调增加函数曲线特征,所以,经验蠕变模型方程中用于描述试验应变-时间关系的函数必须同时具备这 3个特征。而传统 Singh-Mitchell经验蠕变模型采用幂函数来表示应变-时间关系。幂函数的最小二乘法拟合结果显示:幂函数可以同时满足凸函数和单调增加函数的特征,但没有极值,应变随时间不断增长,且在蠕变后期增长较快,曲线较陡,这与上节所得模型计算曲线在蠕变后期较陡、偏离试验曲线的结果一致,与此同时,传统Singh-Mitchell经验蠕变模型蠕变方程应变-时间部分的幂λ为各偏应力下的平均值,只与q=90 kPa时的斜率λ3相近,因此,只有偏应力q=90 kPa下的试验曲线与传统 Singh-Mitchell经验蠕变模型拟合曲线较接近,其他偏应力下模型计算蠕变量与试验结果偏差很大。因此,传统 Singh-Mitchell经验蠕变模型采用幂函数来表示应变-时间关系对于本试验软黏土是不合适的。
解决方案如下:仍用指数函数描述应力-应变关系,将原Singh-Mitchell经验蠕变模型中描述应力-应变关系的指数函数变形为:

式中:εr为极限应变 ε∞,即 ε∞=εr。式(6)并未增加式(3)的待定参数,仍为待定参数 B,β的指数函数,却克服了传统 Singh-Mitchell经验蠕变模型不能描述零应力零应变水平的缺点,即当Dr=0时,εr=0。
通过对应变-时间关系用双曲线函数进行最小二乘法拟合,结果显示同时满足有极值、凸函数曲线特征和单调增加函数曲线特征,与试验软黏土稳定蠕变阶段的应变的衰减特征吻合,因此,本文尝试用双曲线函数替代传统 Singh-Mitchell经验蠕变模型的幂函数来描述本试验软黏土的应变-时间关系,表达式为:

式中:T为待定时间参数;α为极限应变ε∞,即当t=∞时,α=ε∞=εr,代入式(6)得:

将式(8)代入式(7),得修正的Singh-Mitchell蠕变模型方程表达式为:

由式(9)可知:修正的 Singh-Mitchell蠕变模型需要确定的模型参数为B,β和T。
参数T的确定。将式(9)转换成线性形式y=bx+c,可设y=t/ε,x=t,则式(9)变换为:

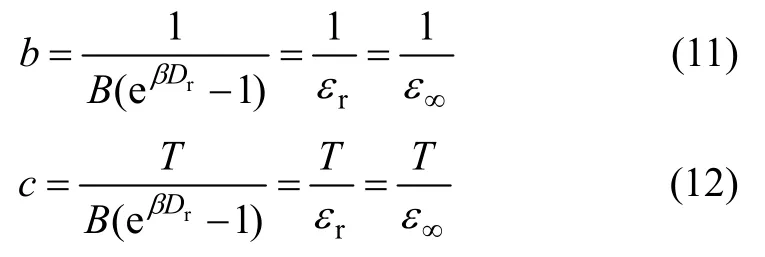
将试验曲线ε-t关系图(图2)转换成y-x关系图,如图6所示。
分别对图6中各偏应力下的数据进行线性拟合,各偏应力下的曲线斜率b和y轴截距c如表2所示。
然后将所得 b,c分别代入式(11)和式(12),可得各偏应力水平下的极限应变ε∞和T。
对T求平均值,即可确定修正Singh-Mitchell蠕变模型的时间参数,见表2。
参数B和β的确定。由于修正的Singh-Mitchell蠕变模型采用如式(6)所示的新的指数函数来描述本三轴蠕变试验软黏土的应力-应变关系,故使用式(6)所代表的指数函数对 ε∞-Dr曲线进行拟合,所得指数拟合曲线与关系式见图7,可得B=0.526 5,β=3.488 3。则本文所建立的围压100 kPa下三轴蠕变试验软黏土的修正Singh-Mitchell蠕变方程的表达式为:
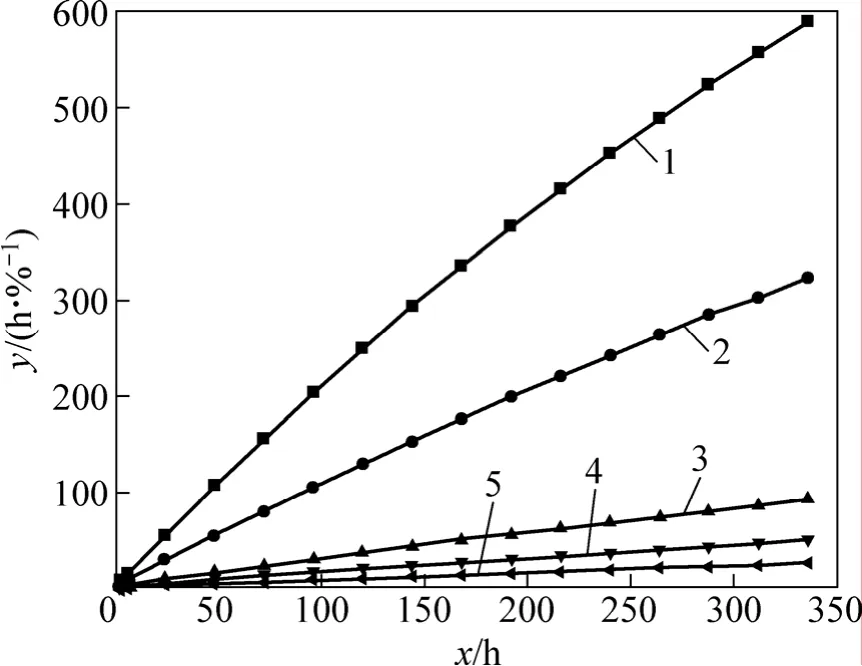
图6 围压为100 kPa下蠕变试验的转换曲线Fig.6 Conversion curves of creep tests under 100 kPa confining pressure

表2 修正Singh-Mitchell蠕变模型的时间参数Table 2 Time parameter of modified Singh-Mitchell creep model

图7 围压为100 kPa下极限应变ε∞与偏应力水平Dr的关系曲线Fig.7 Relation curves between ultimate strain ε∞ and deviatoric stress Dr under confining pressure of 100 kPa

取一定的时间变量,根据三轴蠕变试验结果和式(13)的计算结果可得出围压 100 kPa下修正的Singh-Mitchell蠕变模型计算曲线与试验曲线的比较图,见图8。
由修正的Singh-Mitchell蠕变方程及图8可知:修正的 Singh-Mitchell蠕变模型通过对原Singh-Mitchell蠕变模型描述应力-应变关系的指数函数的改进,使本文所建立的修正的 Singh-Mitchell蠕变模型可以描述从零应变到破坏应变全阶段的应变硬化行为,扩大了原 Singh-Mitchell蠕变模型的适用范围;同时,修正的 Singh-Mitchell蠕变模型计算曲线与试验曲线趋势基本一致,蠕变模型的计算蠕变量随时间的增长而减速增长,并逐渐趋于一极值,与试验软黏土稳定蠕变阶段的应变的衰减特征吻合,蠕变模型的计算结果中除了个别数据与试验结果偏差较大外,绝大多数模型计算数据与试验结果吻合度高,特别是对长期应变的拟合结果较准确,远优于原Singh-Mitchell蠕变模型的拟合结果。
3 结论
(1) 湖南省竹城公路路基软黏土具有明显的蠕变特征,采集该土样制成标准试样,采用梯级荷载加载方法成功地进行了室内三轴固结不排水蠕变试验,获得充足的蠕变试验数据,为检验蠕变模型的精确度提供了依据。
(2) 在各级偏应力下,模型计算结果与试验数据的误差较大,模型不能描述零应力零应变水平,且蠕变量在蠕变后期随时间的增长而增长较快,模型曲线较陡,偏离试验曲线。故采用 Singh-Mitchell经验蠕变模型描述湖南省竹城公路路基软黏土的蠕变特性不合适。
(3) 所建立的修正的Singh-Mitchell蠕变模型与试验结果一致性好,远优于原 Singh-Mitchell蠕变模型的拟合结果,从而验证了本文修正方法的正确性。
[1]Ladd C C, Foot R, Ishihara K, et al. Stress-deformation and strength characteristics[C]//Proceedings of the 9th ICSMFE.Tokyo, 1977: 421-494.
[2]Kabbaj M, Tavenas F, Leroueil S. In situ and laboratory stress-strain relationship [J]. Geotechnique, 1988, 38: 83-100.
[3]Bjerrum L. Engineering geology of Norwegian normallyconsolidated marine clays as related to settlements of buildings[J]. Geotechnique, 1967, 17: 81-118.
[4]Garlanger J E. The consolidation of clays exhibiting creep under constant effective stress[J]. Geotechnique, 1972, 22: 71-78.
[5]Butterfield R. A natural compression law for clays[J].Geotechnique, 1979, 29: 469-480.
[6]Yin J H, Graham J, Elastic visco-plastic modeling of one-dimensional consolidation[J]. Geotechnique, 1996, 46:515-527.
[7]殷建华. 等效时间和岩土材料的弹粘塑性模型[J]. 岩石力学与工程学报, 1999, 18(2): 124-128.YIN Jian-hua. Equivalent time and elastic viscoplastic modeling of geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(2): 124-128.
[8]Singh A, Mitchell J K. General stress-strain-time function for clay[J]. Journal of the Clay Mechanics and Foundation Division,1968, 94(SM1): 21-46.
[9]Mesri G, Rebres-Cordero E, Shields D R, et al. Shear stress-strain-time behaviour of clays[J]. Geotechnique, 1981, 31:537-552.
[10]Lin H D, Wang C C. Stress-strain-time function of clay[J].Journal of Geotechnical and Geoenviromental Engineering, 1998,124(4): 289-296.
[11]王常明, 王清, 张淑华. 滨海软土蠕变特性及蠕变模型[J]. 岩石力学与工程学报, 2004, 23(2): 227-230.WANG Chang-ming, WANG Qing, ZHANG Shu-hua. Creep characteristic and creep model of marine soft soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(2):227-230.
[12]王琛, 唐明, 刘浩吾, 等. 三峡泄滩滑坡滑动带土的Singh-Mitchell蠕变模型[J]. 四川大学学报: 工程科学版,2003, 35(5): 93-95.WANG Chen, TANG Ming, LIU Hao-wu, et al. Creep tests of sliding zone soils of Xietan landslide in Three Gorges[J]. Journal of Sichuan University, 2003, 35(5): 93-95.
[13]朱鸿鹄, 陈晓平, 程小俊, 等. 考虑排水条件的软土蠕变特性及模型研究[J]. 岩土力学, 2006, 27(5): 694-698.ZHU Hong-hao, CHEN Xiao-ping, CHENG Xiao-jun, et al.Study on creep characteristics and model of soft soil considering drainage condition[J]. Rock and Soil Mechanics, 2006, 27(5):694-698.
[14]王琛, 刘浩吾, 许强. 三峡泄滩滑坡滑动带土的改进Mesri蠕变模型[J]. 西南交通大学学报, 2004, 39(1): 15-19.WANG Chen, LIU Hao-wu, XU Qiang. Modified Mesri creep model for the sliding zone soils of Xietan landslide in three gorges[J]. Journal of Southwest Jiaotong University, 2004, 39(1):15-19.
[15]李军世, 孙钧. 上海淤泥质黏土的Mesri蠕变模型[J]. 土木工程学报, 2001, 34(6): 74-79.LI Jun-shi, SUN Jun. Mesri’s creep model for Shanghai silt-clay[J]. Chinese Civil Engineering Journal, 2001, 34(6):74-79.
[16]卢萍珍, 曾静, 盛谦. 软黏土蠕变试验及其经验模型研究[J].岩土力学, 2008, 29(4): 1041-1052.LU Ping-zhen, ZENG Jing, SHENG Qian. Creep tests on soft clay and its empirical models[J]. Rock and Soil Mechanics, 2008,29(4): 1041-1052.
[17]邓志斌. 软黏土蠕变试验与本构模型辨识方法研究及应用[D].长沙: 中南大学资源与安全工程学院, 2007: 10-35.DENG Zhi-bin. Creep test on soft clay and the identification of constitutive model study and its application[D]. Changsha:Central South University. School of Resources & Safety Engineering, 2007: 10-35.
[18]孙钧. 岩土材料流变及其工程应用[M]. 北京: 中国建筑工业出版社, 1999: 113-119.SUN Jun. Creep of geomaterial and its application[M]. Beijing:Chinese Construction press, 1999: 113-119.
[19]维亚洛夫 C C. 土力学的流变原理[M]. 杜余培, 译. 北京:科学出版社, 1987: 297-342.Bялoв C C. Rheologic theory of soil mechanics[M]. DU Yu-pei,trans. Beijing: Science Press, 1987: 297-342.
