基于Kriging法的铁道车辆客室结构优化
2012-07-31谢素超周辉
谢素超,周辉
(1. 中南大学 交通运输工程学院 轨道交通安全教育部重点实验室,湖南 长沙,410075;2. 中南林业科技大学 物流学院,湖南 长沙,410004)
当铁道列车发生碰撞事故后,其撞击过程往往是多辆车的耦合撞击过程,在这个过程中会涉及到乘员与客室结构间的二次碰撞[1-3],并且在二次碰撞过程中,加载条件(如二次撞击速度和冲击加速度等)、客室空间大小、车辆内部部件接触刚度等是影响乘员损伤程度的主要因素[4]。近些年国内外已经开展了一些铁道车辆乘员二次碰撞研究[5-8],如Tyrell等[5,8]开展了一系列的客室内全尺寸假人二次撞击试验与数值模拟研究;Wang等[4,7]利用美国Volpe中心试验的加速度曲线对乘员进行了二次碰撞伤害分析;李兰[6]对原始车体和设计出的耐撞性车体进行了仿真研究,并对乘员进行了二次碰撞研究;但是,对铁道车辆客室结构进行优化设计,到目前为止,国内外还没有相关报道。本研究以乘员损伤参数为目标量,以客室空间尺寸和内部部件接触刚度为设计变量,开展铁道车辆客室结构优化研究,以实现车辆客室空间尺寸、内部部件接触刚度的优化配置,达到保护乘员的目的。而一般在乘员撞击过程中,损伤参数目标量与设计变量间具有很强的非线性关系,很难给出目标参数随设计变量变化的显式方程,这就需要借助代理模型法(Surrogate Model)。建立代理优化模型的方法有多种,常用的方法有传统响应面方法(CRSM)、Kriging模型法(KM)、径向基函数模型法(RBF)等[9-10]。本研究主要采用 Kriging模型构造乘员各损伤参数对各设计变量的响应曲面,通过遗传算法整体寻优方法对代理响应模型寻优,以实现客室结构多目标多参数优化设计的目的。
1 乘员损伤参数(Injury parameters)
为了评价在车辆碰撞事故中的严重程度,有关方面已经进行了很多损伤生物力学以及乘员危险判据的研究[11]。本研究引入2个常用损伤参数:一个是头部损伤准则HIC(Head Injury Criterion),另一个是胸部损伤指标 TC3ms(Thoracic Cumulative-3ms Injury Criterion)。
HIC是目前国际上应用最广泛的头部损伤准则,被许多国家的安全法规和标准所采用,其定义为:
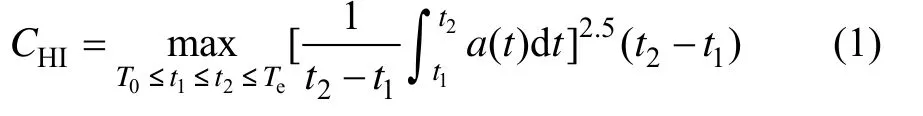
式中:T0为计算初始时间点;Te为计算末时间点;a(t)为时间范围T0≤t≤Te间头部重心的响应加速度(g);t1和t2分别为积分时间间隔内的起始时刻和结束时刻。常用的头部性能指标有CHI15和CHI36,分别表示15 ms和36 ms的时间间隔内的头部损伤指标。
除人体头部之外,胸部也是在碰撞过程中容易受到损伤的1个关键器官。一般当上胸部重心部位受到持续时间不短于3 ms且大小不低于60g的冲击加速度时,就认为胸部受到了严重损伤,这样将该指标定义为累积3 ms损伤指标CT3ms。
除此之外还有颈部损伤准则、腹部损伤参数、大腿和小腿性能指标等。
2 客室结构-乘员模型
本研究基于Madymo建立了车体客室-假人模型,其中假人模型是Madymo中Hybrid Ⅲ 50th假人,车体客室结构模型包括车体地板面、侧墙、座椅坐垫、靠背和桌子,在建模过程中,车体地板面和侧墙采用平板面SURFACE.PLANE来模拟,座椅坐垫、靠背以及桌子采用椭球面SURFACE.ELLIPSOID来模拟,椭球面的方程为:
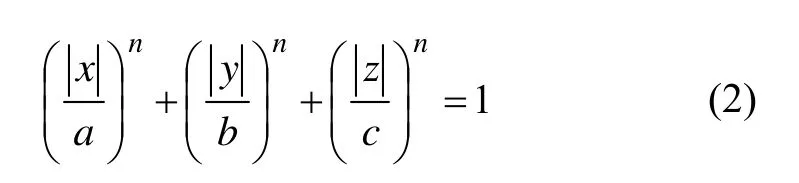
式中:a,b和c为椭球的半轴;n为幂;当n=2时,这个公式描述的是1个椭球,n不断增大,椭球会越来越接近长方体。
假人在客室结构中定位好之后就要定义假人与客室结构间的接触,最终建立的车体客室-假人耦合模型如图1所示。
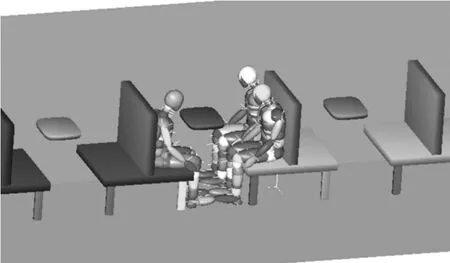
图1 车体客室-假人模型Fig.1 Car body-passenger compartment-dummy model
在该车体客室-假人模型中,客室结构在撞击过程中产生的变形是采用预先定义的运动数据(Prescribed motion data)如接触刚度CHARACTERISTIC. CONTACT进行描述的,这些运动数据一般可以通过碰撞试验或数值模拟得到。本研究车体中各部件的接触刚度是依据美国Volpe国家交通研究中心的试验值,其中桌子接触刚度k1和座椅接触刚度k2分别如表1和表2所示。
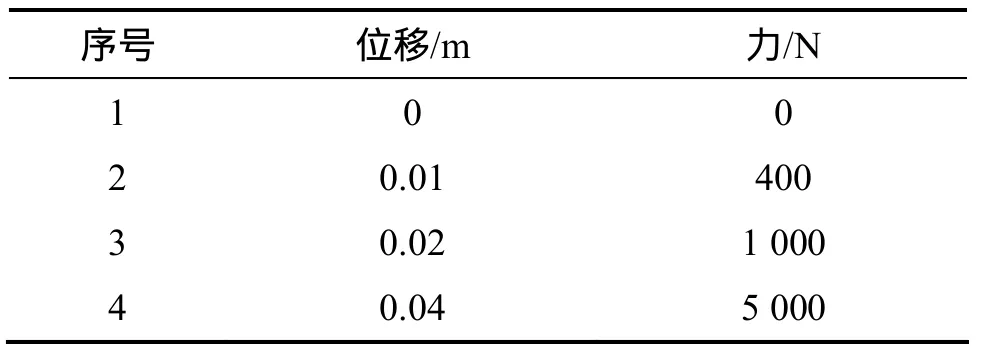
表1 桌子的接触刚度Table 1 Table contact stiffness
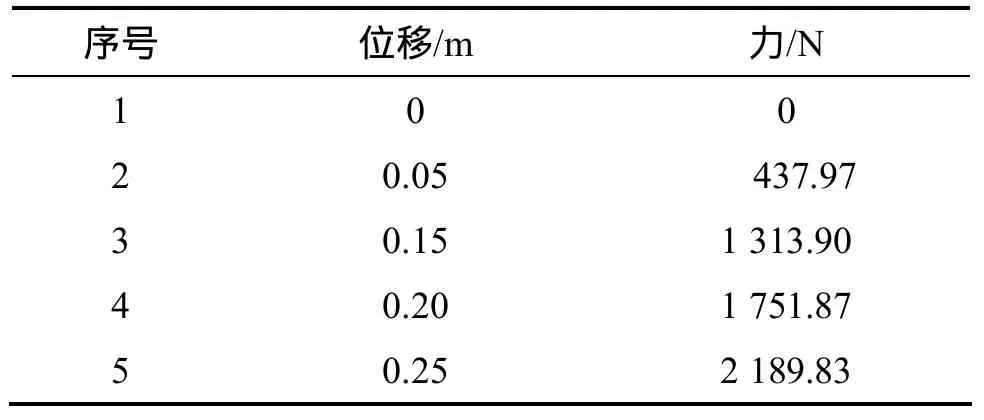
表2 座椅的接触刚度Table 2 Chair contact stiffness
在模型进行计算分析时,需要对模型施加2个加速度场:一个是作用于人体且方向垂直向下的重力加速度场;另一个是水平方向的加速度场,采用美国Volpe国家交通研究中心试验的冲击加速度,如图 2所示,该冲击加速度为三角形脉冲,总持续时间为250 ms,在125 ms时达最大值8g (1g=9.8 m/s2)。
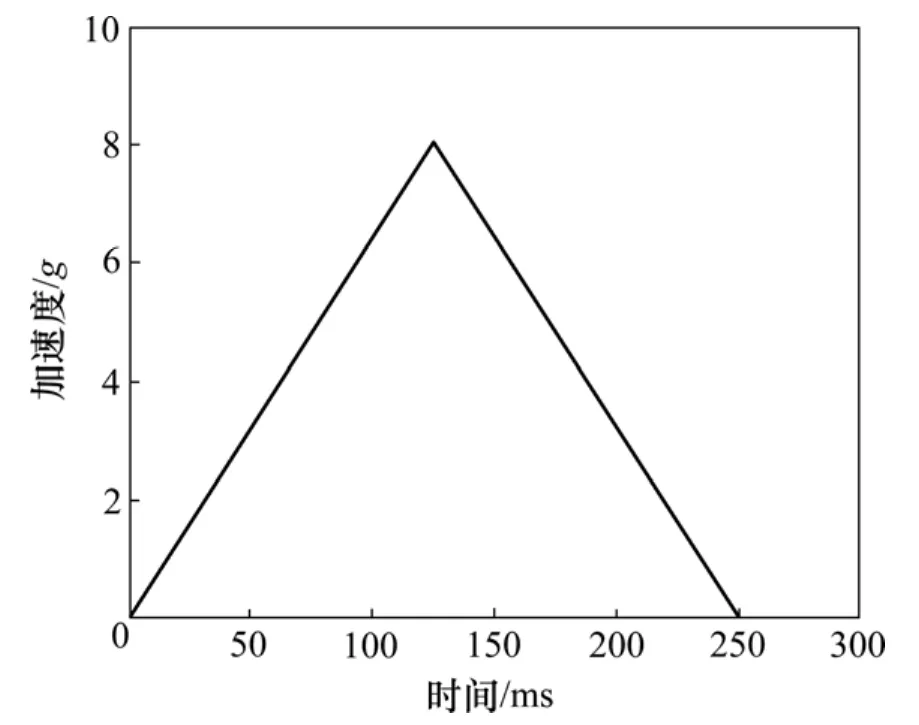
图2 纵向冲击加速度Fig.2 Longitudinal impact acceleration
当列车发生相互接触碰撞后,车内非约束乘员与客室结构间会有相对运动继而发生2次碰撞,在这个过程中影响乘员2次碰撞损伤程度的因素有客室结构空间大小(如图3中小桌的高度h、小桌与座椅的距离l1和座椅的间距l2)和车辆内部部件接触刚度等。而就坐后的乘员与客室间的相互关系有:(1) 乘员对面为桌子;(2) 乘员对面为椅子。所以本研究分别以乘员对面为桌子(座椅-桌子模型)和乘员对面为椅子(座椅-座椅模型)为例,基于Kriging代理优化模型进行客室结构优化研究。
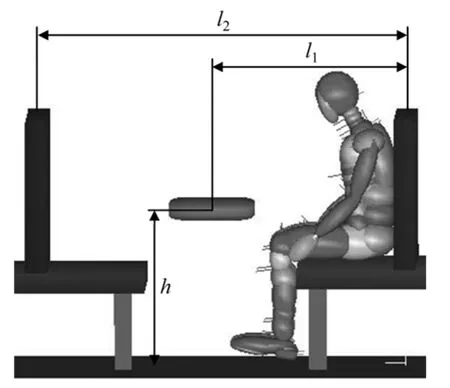
图3 客室空间尺寸Fig.3 Compartment space dimensions
3 Kriging模型基本原理
Kriging模型方法是一种结合试验设计与统计分析的插值算法,可以得到设计变量和目标参数之间的映射关系,并充分考虑了各个参数在变量空间里的相关特征以得到实际问题的精确代理模型[10,12]。
Kriging模型由多项式表示的参数化模型和随机分布函数表示的非参数随机过程模型2部分组成:
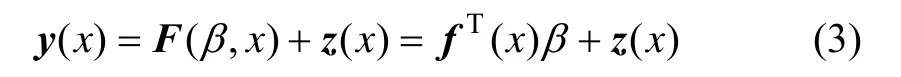
式中:β为回归系数;f(x)是关于设计变量x的多项式;z(x)为随机分布的误差,具有如下统计特性:
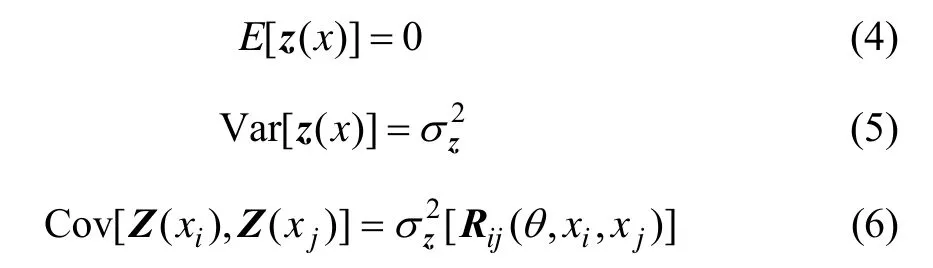
式中:xi和xj为任意2个训练样本为带有参数θ的相关函数。形式有很多种,其中高斯(GAUSS)函数是计算结果最理想而广泛应用的相关函数。

模拟值的误差为:
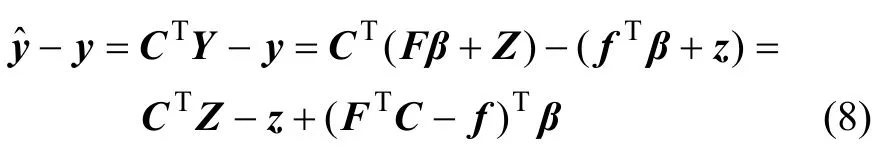

同时,误差的均方差为:
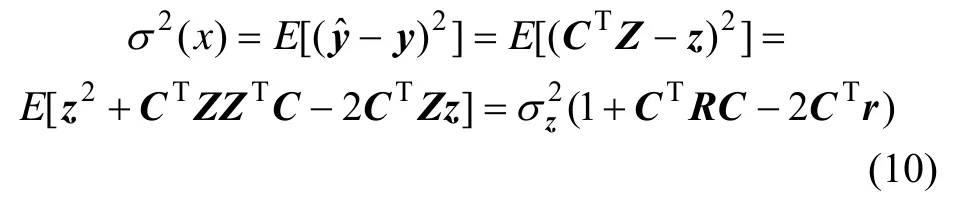
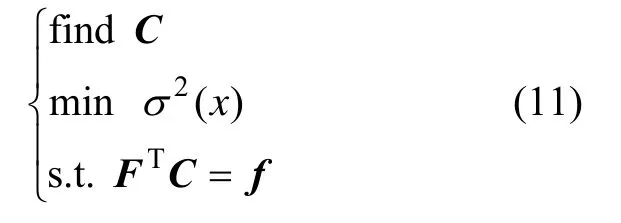
引入Lagrangian乘子:
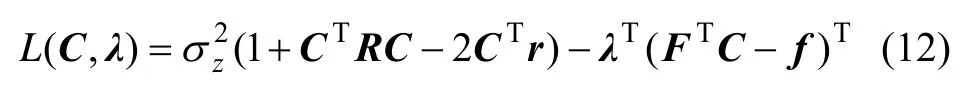
式(12)关于C的梯度为:
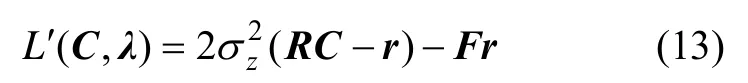
由一阶必要性条件可得:
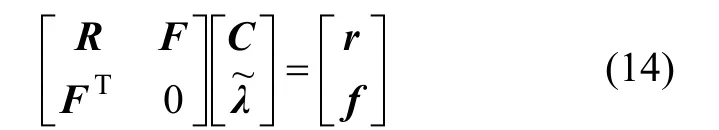
可以得到:
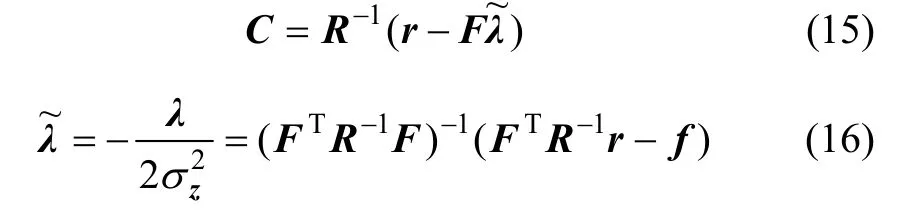
将方程(15)中求得的C代入式(7)中,得到待测点x的响应值
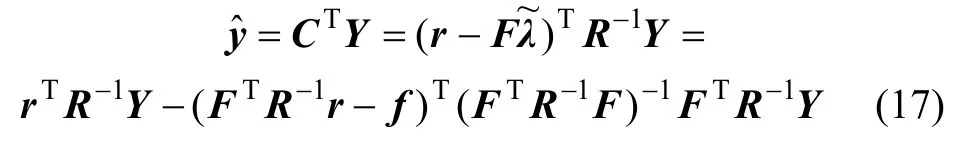
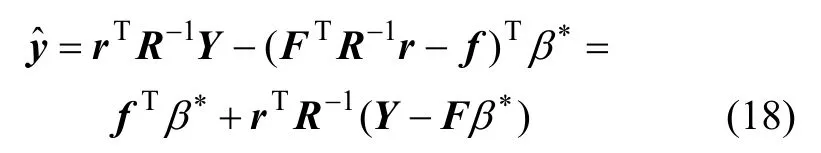
通过求得任意待测点x的f和r可以计算出这一点的响应值。
4 客室结构优化
4.1 座椅-桌子结构优化
当乘员对面有小桌时,乘员与对面小桌发生二次碰撞后,影响乘员二次碰撞损伤程度的因素有小桌高度h、小桌与座椅距离l1以及小桌接触刚度k1等,本研究通过分析这些因素对乘员二次碰撞损伤参数的影响程度,寻求小桌高度h、小桌与座椅距离l1及小桌接触刚度k1的最优配置。该优化问题可描述为:以乘员损伤参数Injury Parameters(包括头部损伤指标CHI15和CHI36,以及胸部损伤指标CT3ms)为目标参数,以小桌与座椅间距l1和小桌高度h为设计变量,在不同的小桌接触刚度(0.5k1,k1,2k1)下,当变化设计变量 l1和h时,利用数值分析求出各个样本点处的乘员损伤参数(CHI15,CHI36,CT3ms),然后基于Kriging法求得乘员损伤参数关于设计变量的代理模型最后通过寻优方法找到使乘员损伤参数达到最小值的代理模型全局最优解。该优化问题用数学方程表示为:

本研究基于2因素5水平的全因子试验设计方法选取了 25个样本进行模拟,当变化设计变量 l1和 h时,通过数值分析,分别得到了在不同的桌子接触刚度(0.5k1,k1,2k1)下,假人损伤参数(如 CHI和 CT3ms)结果。根据设计样本点结果,并基于前面阐述的Kriging代理模型方法,分别构造了假人二次碰撞损伤参数在不同接触刚度下随距离 l1和高度 h的 Kriging模型。图4~6分别为Kriging模型构造的各性能指标(CHI15,CHI36,Cms)的响应曲面,从各响应曲面中可以很直观地看出各性能指标参数随距离l1、高度h以及桌面接触刚度 k1的变化关系:假人的头部性能指标CHI(CHI15及CHI36)和胸部性能指标CT3ms均随接触刚度的增加而增大;其中头部性能指标CHI(CHI15及CHI36)基本随小桌与座椅的距离l1的增加而增大,而随小桌的高度h的增加先变大,在h=0.8~0.85 m时达到最大,继而随高度 h的增加呈变小的趋势;胸部性能指标CT3ms则与小桌与座椅的距离l1及小桌的高度h呈较强的非线性关系。
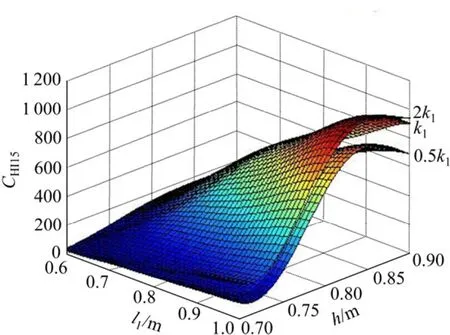
图4 CHI15-Kriging响应面Fig.4 CHI15-Kriging response surface
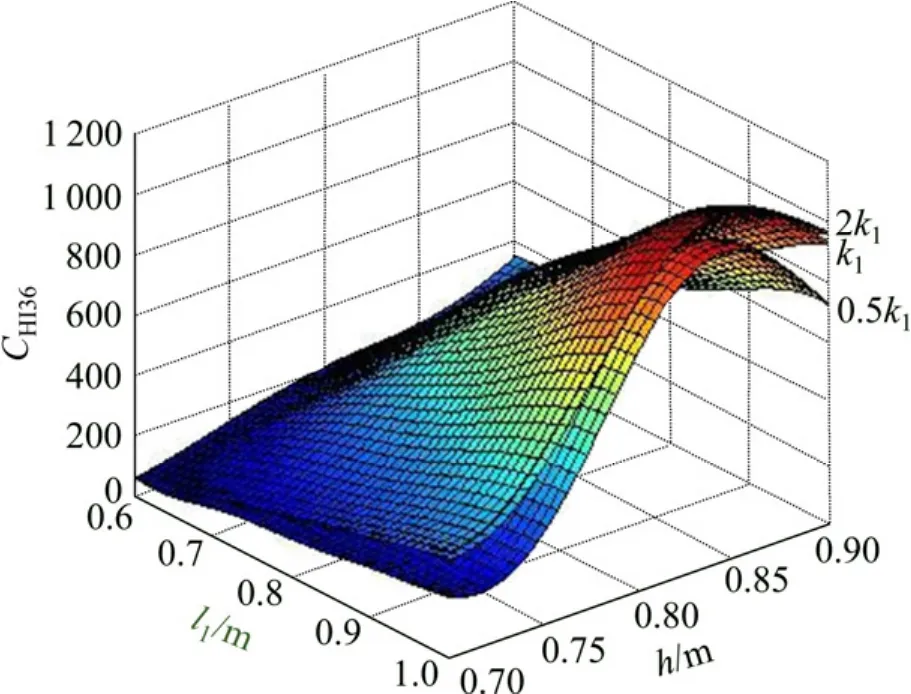
图5 CHI36-Kriging响应面Fig.5 CHI36-Kriging response surface
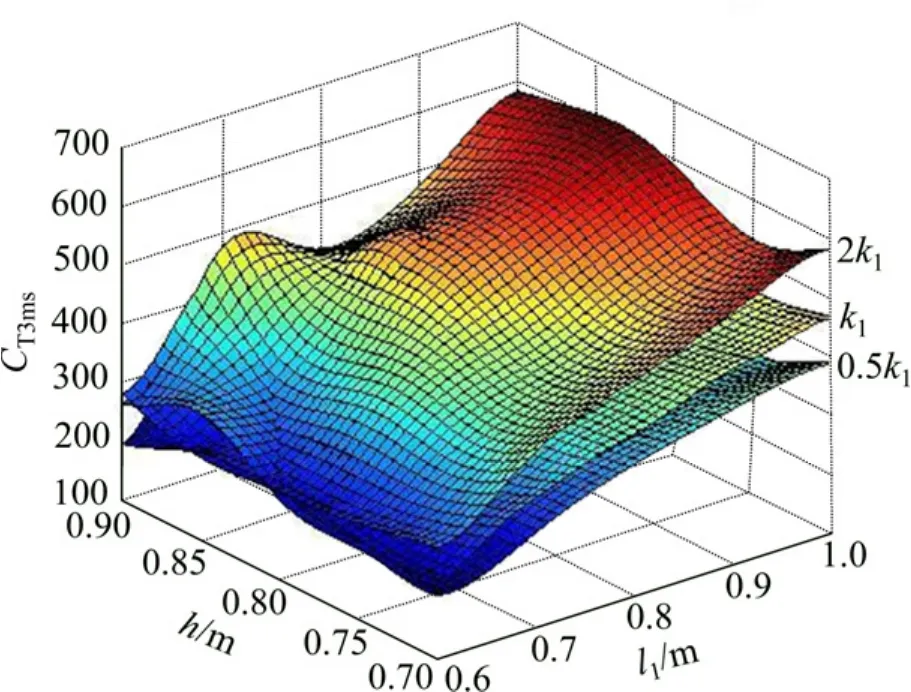
图6 CT3ms-Kriging响应面Fig.6 CT3ms-Kriging response surface
通过前面求得的各损伤参数的 Kriging代理模型(图4~6),除了直观地定性分析各损伤参数与各设计变量的变化规律外,凭观察一般很难找出各损伤参数的确切最大值和最小值,以及出现极值时对应的各设计变量值,这时有必要借助遗传算法(GA)对代理模型进行寻优[13-14],具体步骤如图7所示。
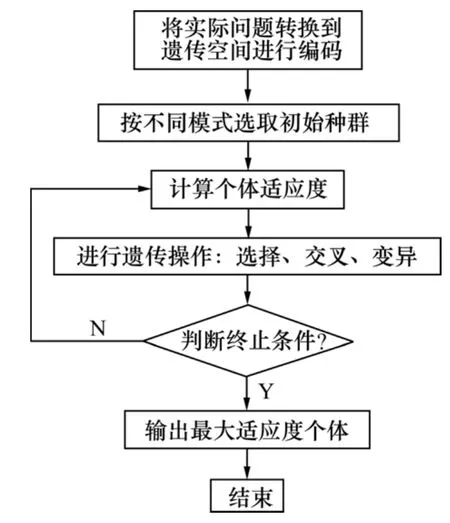
图7 遗传算法整体寻优流程Fig.7 GA overall optimization flow chart
利用图7所示的遗传算法优化程序求解代理模型的全局最大值时,将目标函数转化为适应度函数,然后进行遗传算法的选择、交叉和变异等相关步骤。遗传算法认为生物由低级向高级进化,采用最佳个体保留法,使后代不差于前一代,最终得到最大适应度个体,也即本研究中所求模型的最优值。本研究中该遗传算法优化程序的参数统一选取为:仿真代数为100,种群规模为80,交叉概率Pc=0.8,变异概率Pm=0.05。
通过遗传算法寻优分析,得到接触刚度分别为0.5k1,k1和 2k1时的各损伤参数(CHI15,CHI36及 CT3ms)的最值(最大值(max)和最小值(min)),并与数值模拟的结果进行了误差分析,如表3~5所示。通过分析可知:通过遗传算法对各代理模型的寻优结果与数值计算的模拟结果均吻合地较好,说明寻优结果是可靠的。通过表3可知:桌子接触刚度在0.5k1时的乘员CHI15,CHI36和 CT3ms最优结果(即其最小值)分别为 29.16,55.51和204.64,与对应的数值计算结果相对误差分别为-5.35%,-2.66%和-4.46%。
通过表4可知:桌子接触刚度在k1时的乘员CHI15,CHI36和 CT3ms最优结果(即其最小值)分别为 32.63,63.38和228.77,与对应的数值计算结果相对误差分别为-5.94%,0和-3.79%。
通过表 5可知:桌子接触刚度在 2k1时的乘员CHI15,CHI36和 CT3ms最优结果(即其最小值)分别为42.43,61.49和 197.33,与对应的数值计算结果相对误差分别为-1.74%,0和0。
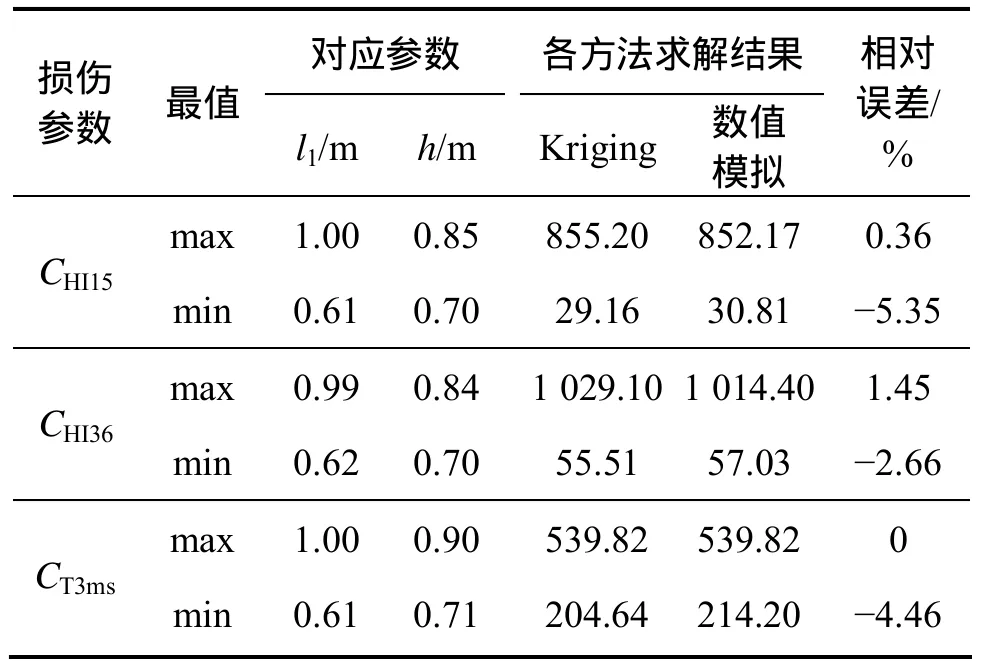
表3 接触刚度0.5k1时的极值分析Table 3 Maximum and minimum value analysis when contact stiffness is 0.5k1
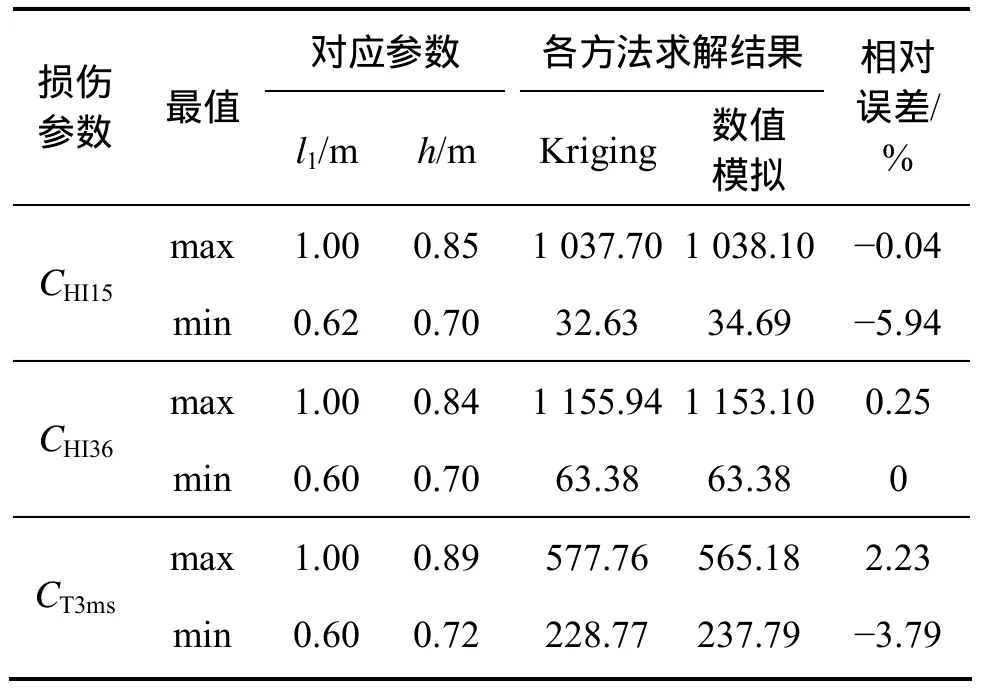
表4 接触刚度k1时的极值分析Table 4 Maximum and minimum value analysis when contact stiffness is k1
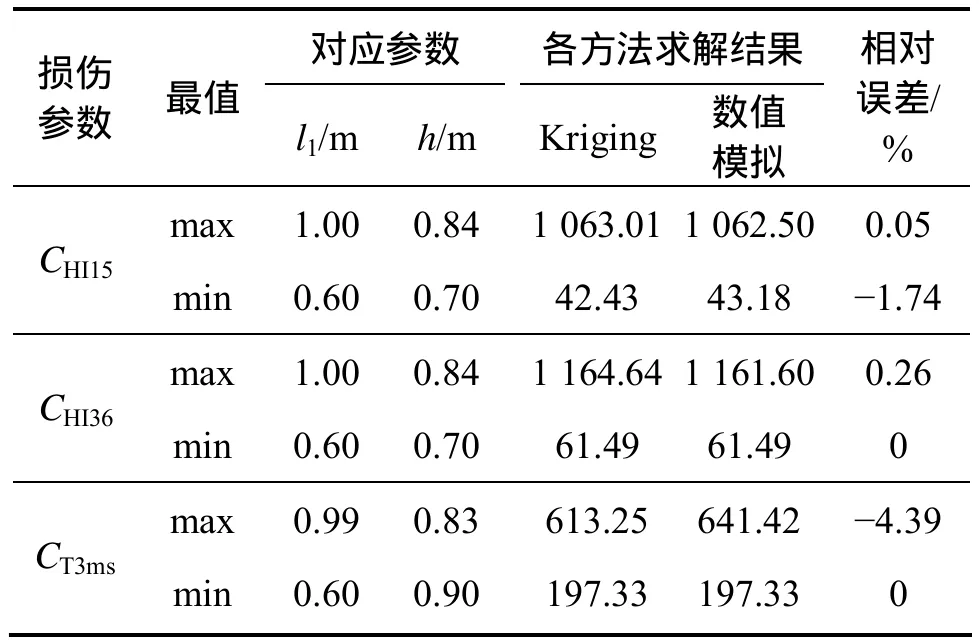
表5 接触刚度2k1时的极值分析Table 5 Maximum and minimum value analysis when contact stiffness is 2k1
图8~9所示为l1=0.60 m,h=0.70 m以及桌子接触刚度0.5k1时乘员与对面桌子发生二次撞击的结果,图8为t=150 ms时假人与桌子发生碰撞时的情形,对应的头部和胸部加速度曲线(图 9)在此时分别达到最大值为 214.13 m/s2和 211.11 m/s2,同时该情况下乘员CHI15,CHI36和CT3ms分别为29.63,61.26和209.39。
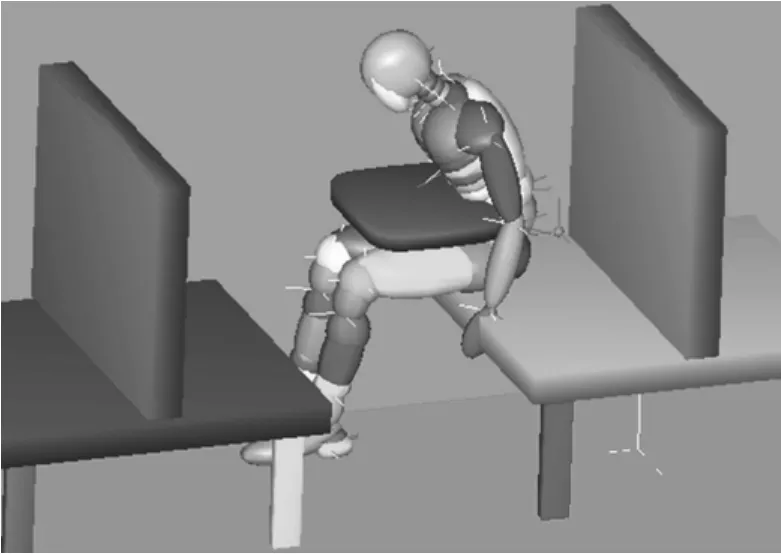
图8 假人撞击情况(t=150 ms)Fig.8 Dummy impact process (t=150 ms)
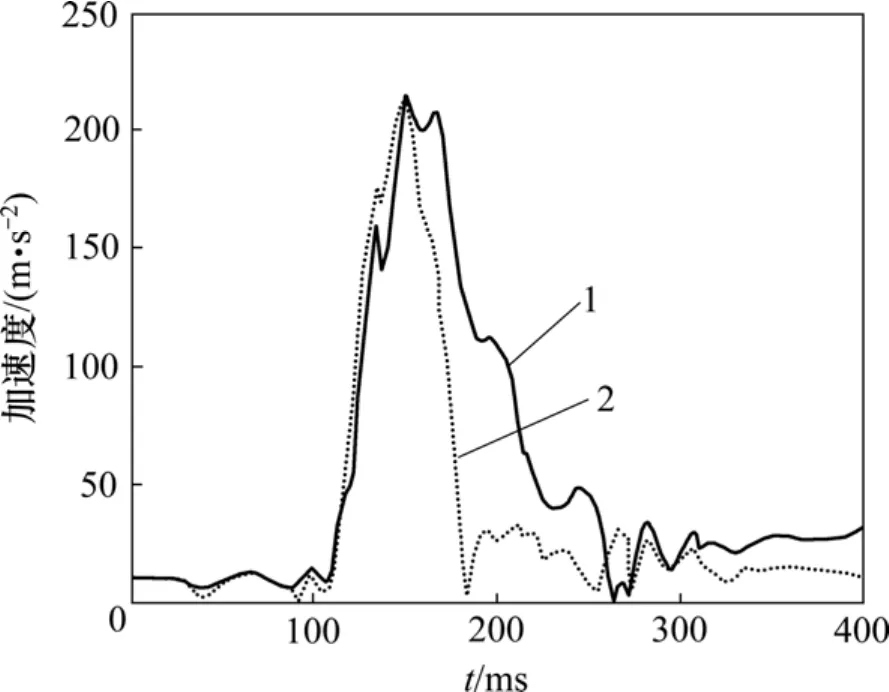
图9 头部和胸部加速度曲线Fig.9 Acceleration curves of head and thorax
4.2 座椅-座椅结构优化
当乘员对面为座椅时,乘员与对面座椅发生二次碰撞后,影响乘员二次碰撞损伤程度的因素有座椅的间距l2以及座椅的接触刚度k2等,本文通过分析这些因素对乘员二次碰撞损伤参数的影响程度,寻求座椅间距l2以及座椅的接触刚度k2最优配置。该优化问题可描述为:以乘员损伤参数(CHI15,CHI36和CT3ms)为目标参数,以座椅间距l2和座椅的接触刚度k2为设计变量,其中k2的变化通过刚度系数(fk)体现。当变化设计变量时,利用数值分析求出各个样本点处的乘员损伤参数(CHI15,CHI36和CT3ms),然后基于Kriging法求得乘员损伤参数关于设计变量的代理模型最后通过寻优方法找到使乘员损伤参数达到最小值的代理模型全局最优解。该优化问题用数学方程表示为:

同样,基于2因素5水平的全因子设计方法选取了25个样本进行模拟,当变化设计变量l2和fk时,通过数值分析,分别得到了假人的损伤参数如头部性能指标CHI和胸部性能指标CT3ms结果。根据设计样本点分析结果,并基于 Kriging代理模型方法分别构造了假人二次碰撞损伤参数在不同l2和fk下的Kriging模型。图10~12所示分别为Kriging模型构造的头部性能指标CHI15,CHI36和胸部性能指标CT3ms的响应面,从各响应曲面中可以看到:假人的头部性能指标CHI(CHI15及CHI36)和胸部性能指标CT3ms均随接触刚度k2的增加而增大,其中头部性能指标CHI(CHI15及CHI36)基本随座椅间距l2的减小而增大,胸部性能指标CT3ms则随座椅间距l2呈较强的非线性关系。
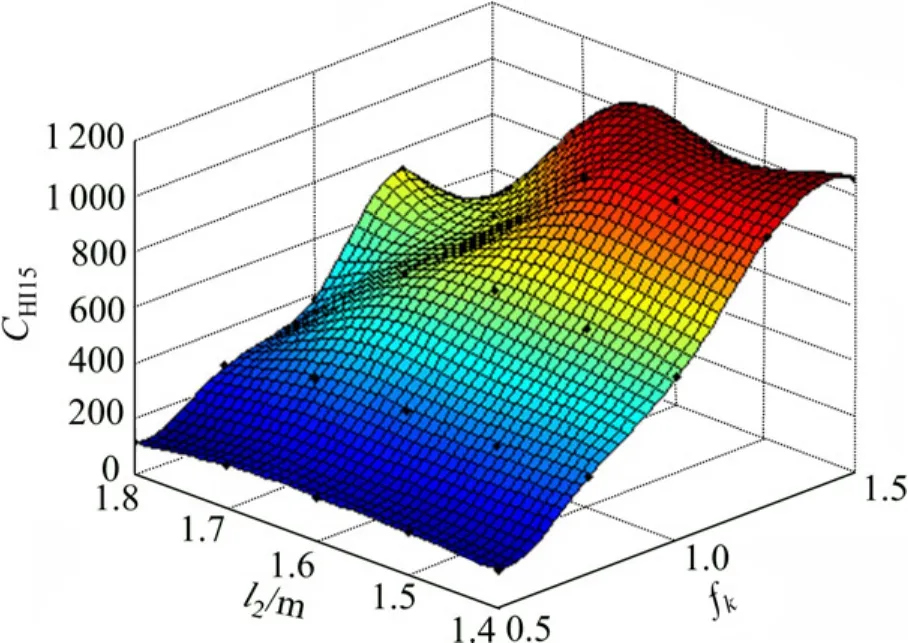
图10 CHI15-Kriging响应面Fig.10 CHI15-Kriging response surface
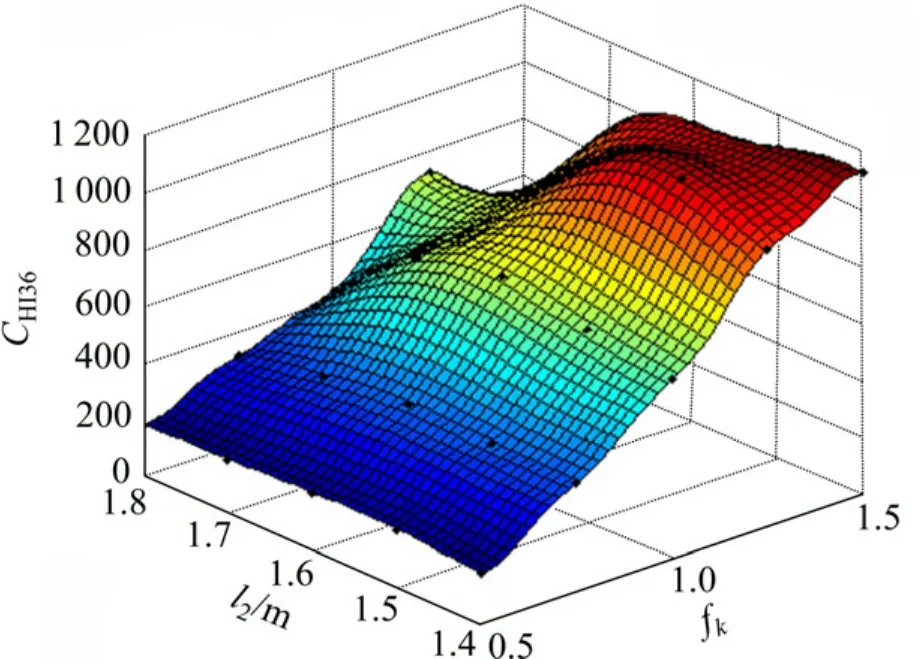
图11 CHI36-Kriging响应面Fig.11 CHI36-Kriging response surface
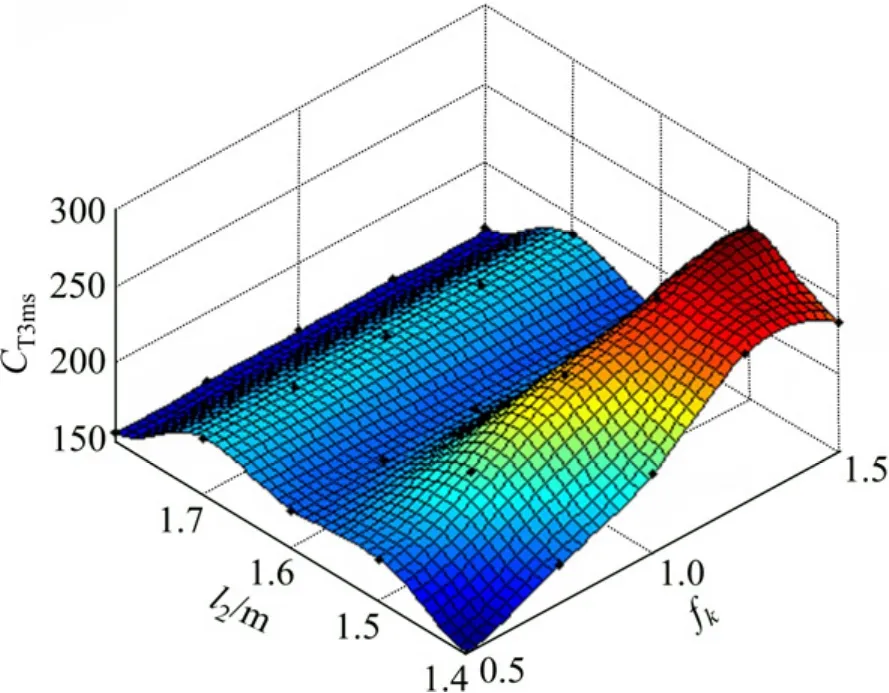
图12 CT3ms-Kriging响应面Fig.12 CT3ms-Kriging response surface
为了求得不同l2和fk下的各损伤参数的确切最大值和最小值,以及出现极值时对应的各设计变量值,同样引入遗传算法对各代理模型进行寻优。通过遗传算法寻优分析,得到各损伤参数(CHI15,CHI36及CT3ms)的极值,以及出现极值时对应的l2和fk,并与数值模拟的结果进行对比分析,如表6所示。乘员CHI15,CHI36和 CT3ms的最优结果(即其最小值)分别为 114.52,179.17和150.91,对应的fk和l2分别为0.52和1.80 m,0.51和1.40 m与0.50和1.40 m,此时的数值计算结果相对误差分别为-4.32%,-3.34%和0,通过遗传算法对各代理模型的寻优结果与数值计算的模拟结果均吻合地较好,说明该寻优结果是可靠的。
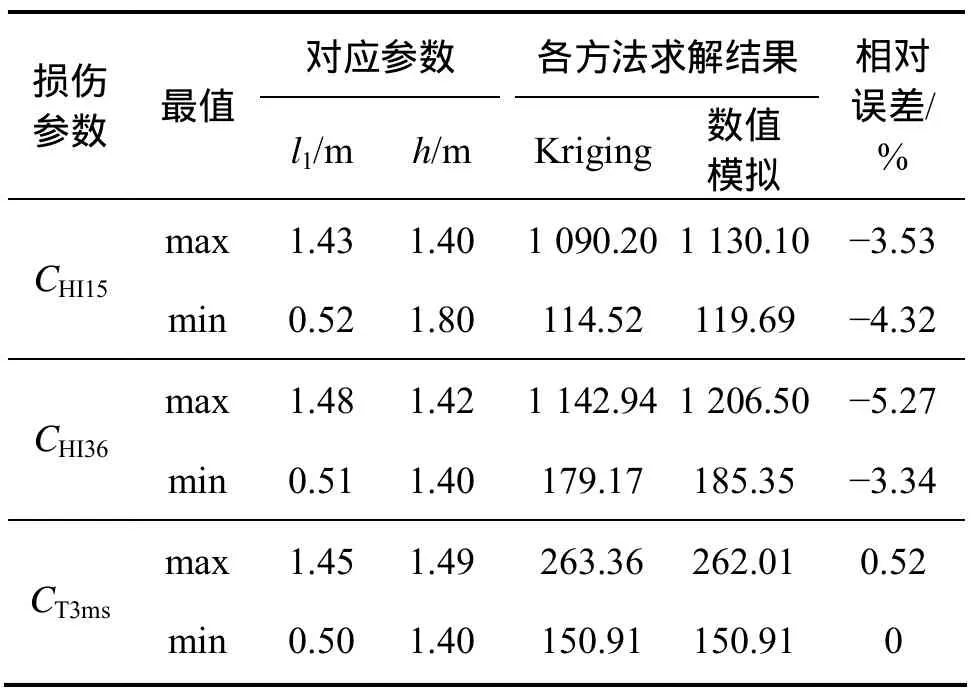
表6 各损伤参数最值分析Table 6 Maximum and minimum value analysis of each injury parameters
图13~14所示为fk=0.50,l2=1.40 m时乘员与对面座椅发生二次撞击的结果,图13(a)为t=172 ms时假人膝盖撞上座垫时的情形,对应的头部和胸部加速度曲线(图14)在此刻分别达到第1个峰值184.29 m/s2和154.37 m/s2;随着时间的推移,t=237 ms时假人头部撞上座椅靠背(图13(b)),此时头部加速度曲线达到最大峰值494.28 m/s2;同时,在该情况下,乘员CHI15,CHI36和CT3ms分别为140.78,179.94和150.91。
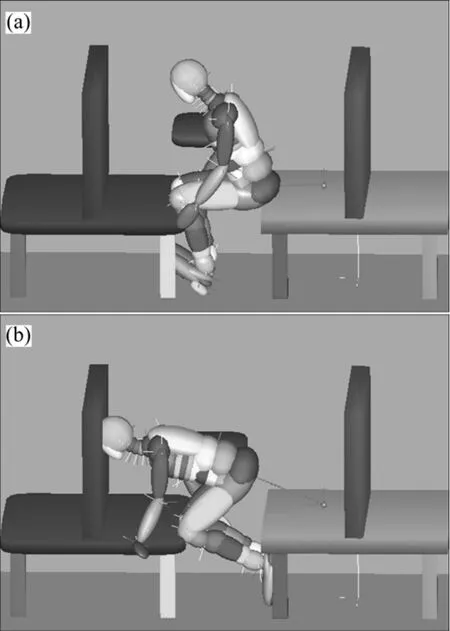
图13 假人撞击情况Fig.13 Dummy impact process
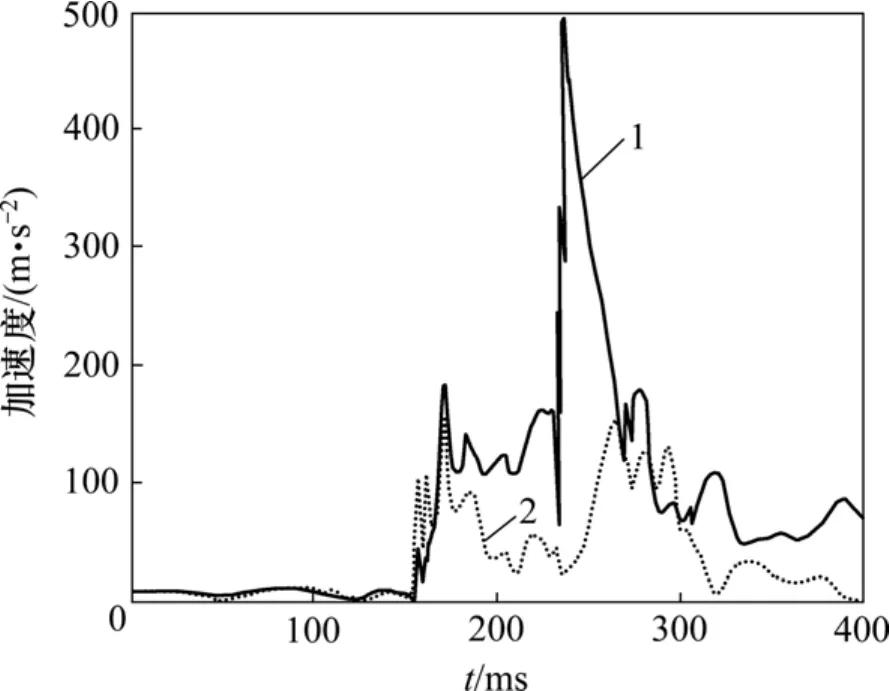
图14 头部和胸部加速度曲线Fig.14 Acceleration curves of head and thorax
5 结论
(1) 将Kriging代理优化模型运用到铁道车辆客室结构优化研究中,得到了目标参数(CHI15,CHI36和CT3ms)关于设计参数(小桌的高度h、小桌与座椅的距离l1、座椅的间距l2以及小桌接触刚度k1和座椅接触刚度k2)比较理想的响应曲面,以实现多目标多参数结构非线性优化目的。
(2) 基于遗传算法对建立的目标参数代理模型进行整体寻优,得到了比较理想的优化结果。座椅-桌子结构模型的寻优结果表明:桌子接触刚度在0.5k时的乘员 CHI15,CHI36和 CT3ms最优结果分别为29.16(l1=0.61 m,h=0.70 m),55.51(l1=0.62 m,h=0.70 m)和204.64(l1=0.61 m,h=0.71 m);桌子接触刚度在k时的乘员 CHI15,CHI36和 CT3ms最优结果分别为32.63(l1=0.62 m,h=0.70 m),63.38(l1=0.60 m,h=0.70 m)和228.77(l1=0.60 m、h=0.72 m);桌子接触刚度在2k时的乘员 CHI15,CHI36和 CT3ms最优结果分别为42.43(l1=0.60 m,h=0.70 m),61.49(l1=0.60 m,h=0.70 m)和197.33(l1=0.61 m,h=0.90 m)。座椅-座椅结构模型的寻优结果表明:乘员CHI15,CHI36和CT3ms的最优结果分别为 114.52(fk=0.52,l2=1.80 m),179.17(fk=0.51,l2=1.40 m)和 150.91(fk=0.50,l2=1.40 m)。
(3) 通过遗传算法对各代理模型的寻优结果与数值计算的模拟结果均吻合得较好,误差范围为-5.94%~2.23%,说明基于本研究中Kriging代理模型的优化结果是可靠的。
[1]Simons J W, Kirkpatrick S W. High-speed passenger train crashworthiness and occupant survivability[J]. International Journal of Crashworthiness, 1999, 4(2): 121-132.
[2]Dias J P, Pereira M S. Optimization methods for crashworthiness design using multibody models[J]. Computers & structures, 2004,82(17): 1371-1380.
[3]Kirkpatrick S W, Schroeder M, Simons J W. Evaluation of passenger rail vehicle crashworthiness[J]. International Journal of Crashworthiness, 2001, 6(1): 95-106.
[4]Wang W B. Influence factors of railway vehicle interior impact injury[J]. Applied Mechanics and Materials, 2011, 79: 227-231.
[5]Tyrell D C, Severson K J, Marquis B P. Train crashworthiness design for occupant survivability[R]. San Francisco: AmericanSociety of Mechanical Engineers, Applied Mechanics Division,AMD, 1995.
[6]李兰. 城轨车辆耐碰撞结构设计及其乘员安全数字仿真研究[D]. 北京: 铁道部科学研究院, 2007: 67-80.LI Lan. Research on designing crashworthy structure for urban rail vehicle and occupant safety by simulation method[D].Beijing: China Academy of Railway Sciences, 2007: 67-80.
[7]王文斌, 赵洪伦, 刘学军. 轨道车辆乘员二次碰撞伤害的研究[J]. 城市轨道交通研究, 2007, 10(9): 23-27.WANG Wen-bin, ZHAO Hong-lun, LIU Xue-jun. Railway vehicle occupant’s injury caused by the impact second[J]. Urban Mass Transit, 2007, 10(9): 23-27.
[8]Severson K, Tyrell D, Perlman A B, et al. Rail passenger equipment collision tests: analysis of structural measurements[R].Orlando, Florida: American Society of Mechanical Engineers,Applied Mechanics Division, 2000.
[9]Forsberg J, Nilsson L. Evaluation of response surface methodologies used in crashworthiness optimization[J].International Journal of Impact Engineering, 2006, 32(5):759-777.
[10]Forsberg J, Nilsson L. On polynomial response surfaces and Kriging for use in structural optimization of crashworthiness[J].Structural and Multidisciplinary Optimization, 2005, 29(3):232-243.
[11]ATOC AV/ST9001. Vehicle interior crashworthiness[S].
[12]Lanzi L, Airoldi A, Chirwa C. Application of an iterative global approximation technique to structural optimizations[J].Optimization and Engineering, 2009, 10(1): 109-132.
[13]Sekulski Z. Multi-objective topology and size optimization of high-speed vehicle-passenger catamaran structure by genetic algorithm[J]. Marine Structures, 2010, 23(4): 405-433.
[14]SONG Xiao-lin, LI Ye-song, MAO Kai-nan, et al. Optimization calculation of the steering knuckle structure of vehicle based on Genetic Algorithm and MATLAB-ADAMS[J]. Journal of Hunan University Natural Sciences, 2010, 37(7): 32-36.
