基于最大熵原理与最优化方法的隧道衬砌结构可靠度分析

张道兵 ，杨小礼，朱川曲，王卫军

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 煤矿安全开采技术湖南省重点实验室，湖南 湘潭，411201)

由于隧道衬砌结构的参数具有随机性，其分布具有多样性，且极限状态功能函数具有高度非线性的特征，所以，在进行其可靠度计算中，要从参数估计、极限状态功能函数和结构可靠度计算方法这3个方面进行考虑，任何一方面的较大误差都会给计算结果带来较大偏差，从而影响计算结果的准确性。在参数估计方面，最常用的确定变量概率分布的方法是先假设随机变量的概率分布，然后，通过检验来确定拒绝或不拒绝假设，或者按照主观经验来认定数据是否服从某种分布。这些做法给处理结果添加了主观因素，使得结果与客观事实相偏离。而运用最大熵原理可通过数据样本估计出最接近真实情况、不添加任何主观因素的概率密度分布，保证参数估计的准确性。在可靠度计算方法方面，目前主要有蒙特卡罗数值模拟法、随机有限元法、响应面法[1]、矩法(包括一次二阶矩法[2]、一次三阶矩法[3]、二次二阶矩法[4]、二次四阶矩法等)、最优化法共5类。针对隧道衬砌结构，其极限状态功能函数是高度非线性的，若采用矩法计算结构的可靠度，需要求极限功能函数的导数，不仅计算量很大，而且当功能函数高度非线性时，矩法精度低，存在一定的误差；若采用随机有限元、响应面法和蒙特卡罗数值模拟法计算其结构可靠度，需编制专门的程序，计算较复杂，要求掌握编程语言的算法和编程技巧，难度比较大。即使在Matlab环境下实现蒙特卡罗法直接抽样计算可靠度[5-6]，也需要掌握 Matlab的语法和编程技巧。到目前为止，运用最优化原理求解可靠度指标的方法很多，如梯度下降法、惩罚函数法、序列二次规划法、Lagrange乘子法、H-L法及其改进H-L法等，并对各种优化进行了验证。但这些最优化法对算法和编程要求高，且效率低，程序通用性较差，对一般工程技术人员来说，具有相当的难度。也有一些研究者直接利用 Matlab优化工具箱实现最优化方法计算结构可靠度指标，但由Matlab优化工具箱中的所有函数 (除 linprog之外)得到的仅是局部优化解，要求所求模型必须为凸规划模型[7]，计算结果才是准确的，而隧道衬砌结构可靠性模型不符合凸规划条件，为此，本文作者根据可靠度指标的几何意义，建立隧道衬砌结构可靠度指标计算的优化模型，利用Microsoft Excel中的规划求解器进行可靠度指标的优化求解，弥补了上述各计算方法的不足，快速、有效地计算出隧道衬砌结构的可靠度指标，并采用蒙特卡罗100万次直接抽样法对结果进行了验证，证实其结果精确度高，适用性好。在极限状态功能函数方面，采用现行隧道设计规范的衬砌截面抗拉和抗压检算式，建立衬砌截面抗拉极限状态方程和抗压极限状态方程。本文在该极限状态功能函数的基础上，采用最大熵原理计算得出衬砌结构参数的统计特征，并利用Microsoft Excel的规划求解器直接由最优化方法计算其结构可靠度，且采用蒙特卡罗法对结果进行验证。

1 基于最大熵原理的概率密度函数的确定与拟合检验

1.1 概率密度函数的确定

最大熵原理的定义为：在所有满足给定约束条件下的许多概率密度函数中，信息熵最大的密度函数就是最佳密度函数[8]。熵最大意味着人为假定最小，从熵作为不确定性的度量来看， 此时解包含的主观成分最少，因而是最客观的[9]。其表达式可写为：

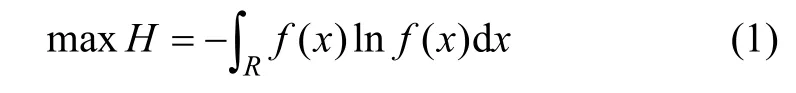
其满足约束条件为：

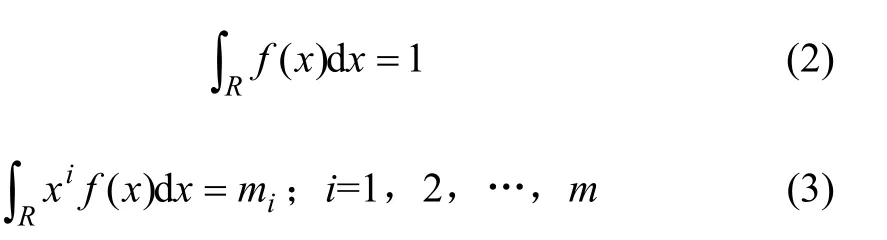
式中：f(x)为概率密度函数；R为积分区间；m为所用矩的阶数；mi为样本的第i阶原点矩。

采用经典微积分方法，并引入拉格朗日算子，可求得最大熵密度函数解析式为：

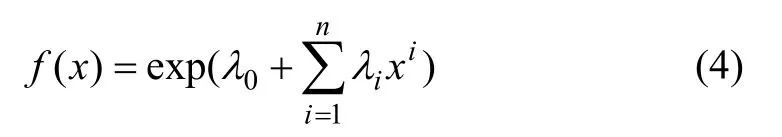
式中：λ0，λ0，…，λm为拉格朗日乘子。

根据式(4)，只要确定参数λ就可以完全确定f(x)，为了便于数值求解，经数学变换可得到：

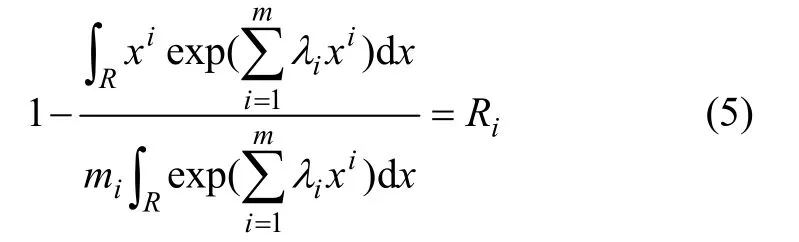
式中：Ri为残差，可以用数值计算的方法把它减小到接近于0。用非线性规划求这些残差平方和的最小值，就可以得到问题的解：

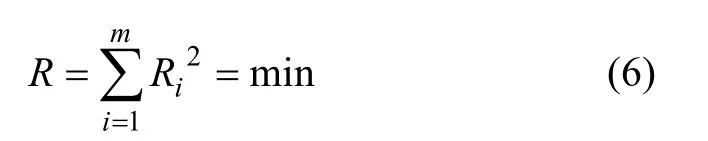
当R＜ε或所有的|Ri|＜ε时(其中，ε为规定的允许误差)，则认为上式收敛。

1.2 拟合检验

根据最大熵原理求得的最大熵密度函数必须通过拟合良好性检验，才能从理论上确定是否能够反映随机变量真实的概率特性。可选用精度高的K-S检验法(或A-D检验法)，把随机变量的实测数据拟合到一个常用的较为合适的分布上，然后，通过对经验分布函数与假设理论分布函数的检验来确定拒绝或是接受假设。其检验步骤为[10]：

(1) 设由样本矩求得的最大熵密度函数式f(x)积分得到总体的概率分布函数为F(x)，假设：F(x)=F0(x)；

(2) 设经验概率分布函数为Fn(x)，计算统计量

(3) 给定显著性水平α，通常取α=0.10或α=0.05；

(4) 根据α和样本容量n在K-S 检验表上查得临界值Dn,α；

(5) 统计推断：当Dn≤Dn,α时，则接受原假设分布；当Dn＞Dn,α时，否定原假设，选用另一种概率分布。

2 最优化方法计算可靠度指标的数学模型与映射变换

2.1 数学模型

结构可靠度的最优化方法是指从结构可靠度指标的几何含义出发，采用可靠度指标的优化数学模型，直接求解目标函数值(可靠度指标)的结构可靠度计算方法。设X1，X2，…，Xn是结构中n个任意分布的独立随机变量,由这些随机变量表示的结构极限状态方程为：

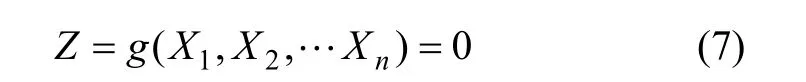
采用R-F(拉科维茨-菲斯莱法)法将非正态变量当量正态化,得到等效正态分布的均值及可靠度指标

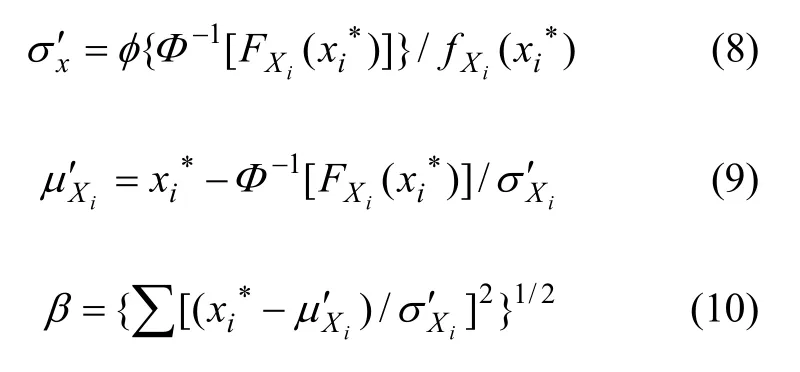
根据结构可靠度指标的几何意义，优化模型可表示为：

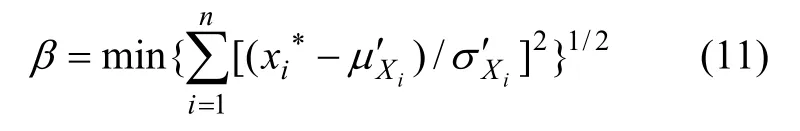
约束条件为：

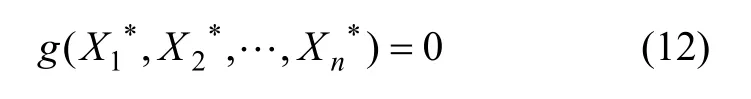
由此将求解可靠度指标β的问题转化为有约束条件下的极小值问题。即在式(12)的约束条件下所确定的可行域内搜索式(11)的最优解，β的最小值即为可靠度指标。

2.2 分布的映射变换

可靠度指标β是指标准化正态坐标系中原点到极限状态曲面的最短距离，因此，需要将非标准正态随机变量Xi映射为标准正态随机变量Yi。对于隧道衬砌结构参数中的正态分布和对数正态分布，可进行如下映射变换。

(1) 当Xi服从正态分布时，

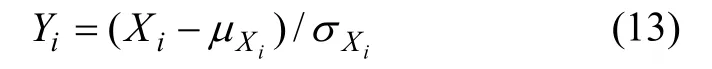
(2) 当Xi服从对数正态分布时，lnXi服从正态分布，

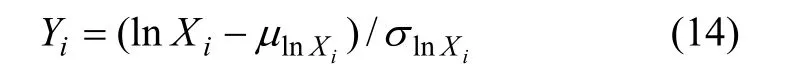
2.3 Microsoft Excel规划求解器实现最优化方法计算可靠度指标的步骤

规划求解是Excel工作表软件的一个加载工具，用于求解复杂的方程及各类线性或非线性有约束优化问题。其计算可靠度指标的步骤为：新建1个Excel 表格，首先在A单元格中依次输入变量名称，在B单元格中依次输入对应变量符号，在C1单元格中输入目标函数(在Excel规划求解工具中，包含公式的目标单元格代表的是目标函数)β的计算公式，在C2，C3，…，Ci单元格中输入决策变量X1，X2，…，Xn(在Excel规划求解工具中，可变单元格代表的是决策变量)的初值，一般可设初值为 0，如果变量为分母或取对数可设初值为1；然后，选择 “工具” 栏中的 “规划求解”选项，在“约束”栏中“添加”约束条件(用单元格表示)，并在“选项”按钮中根据需要设置迭代方法、精度、允许误差、收敛度；最后，在对话框中选择目标单元格的值为“最小值”，单击对话框右上的“求解” 按钮，弹出 “规划求解结果” 对话框，得到可靠指标β及正态空间中的验算点Y*，得到结果，计算结束。

3 隧道衬砌结构的极限状态方程与优化模型

根据现行隧道设计规范的衬砌截面抗拉和抗压检算式，建立衬砌截面抗拉极限状态方程和抗压极限状态方程，抗拉极限状态属正常使用极限状态，而抗压极限状态则属承载能力极限状态。

(1) 当偏心矩e0≤0.2t(t为衬砌厚度)时，截面由抗压强度控制承载能力，相应的抗压极限状态方程为：

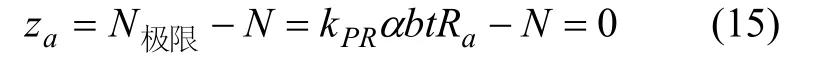
式中：N极限为衬砌混凝土所能承受的极限轴力(即抗力)；N为计算所得的截面轴力(即载荷效应)；kPR为抗力计算模式不定性；b为纵向宽度，取1 m；t为截面厚度；α为偏心影响系数；Ra为混凝土抗压强度。

偏心影响系数α的概率分布为正态分布，均值和变异系数计算公式为：

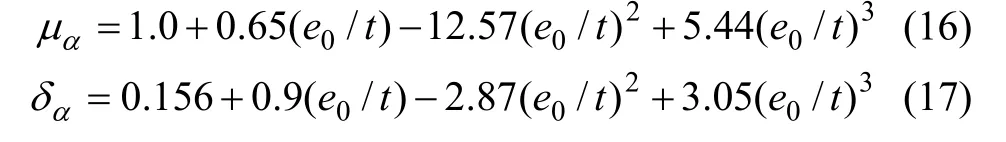
其优化模型为：

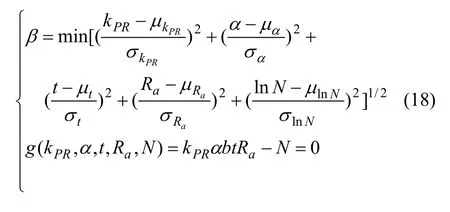
(2) 当偏心矩e0＞0.2t时，截面由抗拉强度控制承载能力，相应的抗拉极限状态方程为

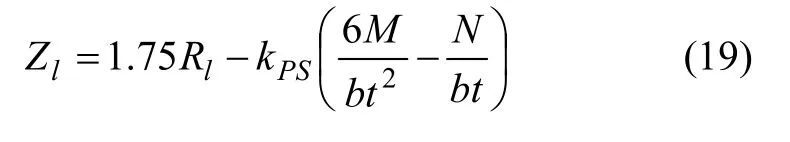
式中：M为计算所得截面弯矩；RI为混凝土极限抗拉强度；kPS为荷载效应计算模式不定性；其余变量含义同上。

其优化模型为：

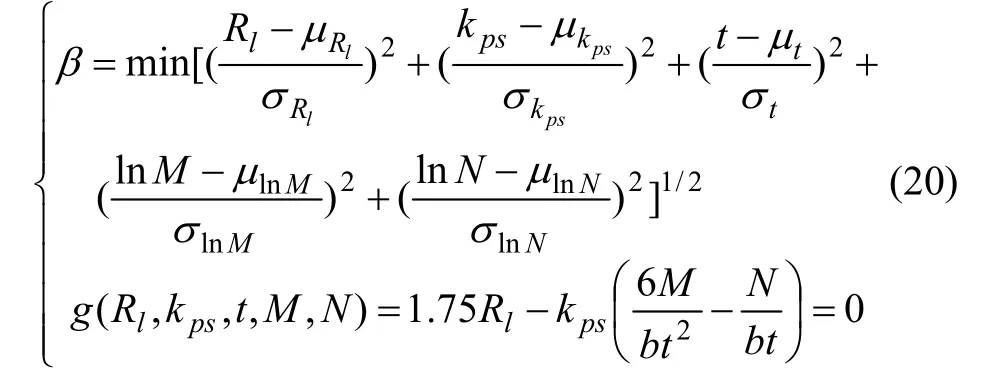
上述极限状态方程中，荷载效应N和M的可由蒙特卡罗有限单元法求得，其统计特征可由最大熵原理求得，其他随机变量的值可通过大量的现场调查、试验获得，其统计特征由最大熵原理求得。

4 工程计算

以四川1个铁路工程隧道某段为例。该段围岩较软，裂隙发育，岩体不完整。按照单线铁路隧道衬砌标准进行设计，根据蒙特卡罗有限单元法、现场调查、测量、实验室试验获得原始数据。

现以隧道衬砌厚度为例进行统计特征估计。采用探地雷达测得50个衬砌厚度，其样本平均值为0.600 1 m, 标准差为0.090 2，通过前面所述方法求解其最大熵密度函数为：

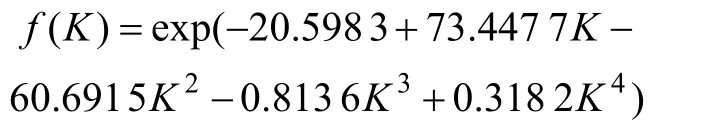
其中：残差平方和R为8.28×10-6。由K-S法进行检验, 假设样本服从正态分布，统计量Dn=0.064 08。给定显著性水平α= 0.10，样本容量n=50，由K-S检验表上查得临界值Dn,α=0.169 59。Dn＜Dn,α，所以，接受原假设，并可判定衬砌厚度为正态分布。

同理，依次可求得其它参数的统计特征，如表1所示。

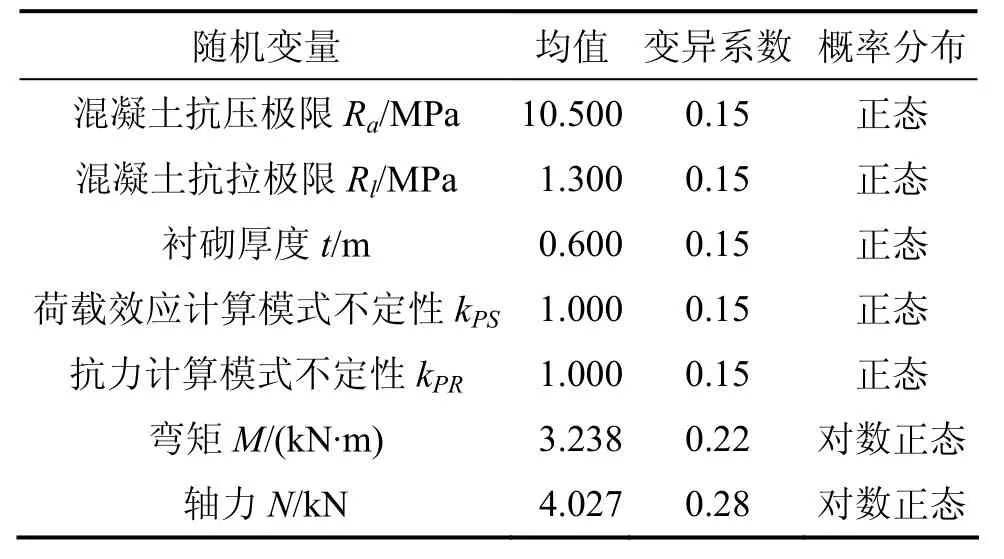
表1 基本随机变量统计特征Table 1 Probability property for basic random variable

按承载能力抗压极限状态和抗拉极限状态分别建立隧道衬砌结构极限状态方程，将上述参数代入式(18)和(20)，按照Microsoft Excel规划求解器实现可靠度指标计算步骤，且设置迭代方法为牛顿法，精度为0.000 001，允许误差0.1%，收敛度为0.000 1，可得：抗压可靠度指标βra=4.474 3，抗拉可靠度指标βrl=2.108 8；在普通双核计算机上运行的时间为0.6 s。

采用蒙特卡罗法 100万次直接抽样法计算结果为：βra=4.473 9，βrl=2.108 3。前者计算结果与此结果非常接近。并与文献[11]中建议的目标可靠指标4.200 0和2.000 0比较，该隧道衬砌结构的可靠度能满足工程可靠性要求。其主要参数(衬砌厚度t、衬砌厚度的变异系数Vt、混凝土抗拉极限Rl、混凝土抗拉极限的变异系数弯矩M的变异系数VM、轴力N的变异系数VN、混凝土抗压极限Ra)与可靠度的关系曲线如图1～7 所示(其中以式(14)进行计算，VN和Ra以式(12)进行计算)。

(1) 从图1、图2可知：隧道衬砌厚度对结构可靠度指标影响非常大，是影响结构可靠度的主要参数。

(2) 从图3、图4、图7可知：混凝土抗拉极限与混凝土抗压极限及其变异系数对可靠度指标有一定的影响，但不显著。

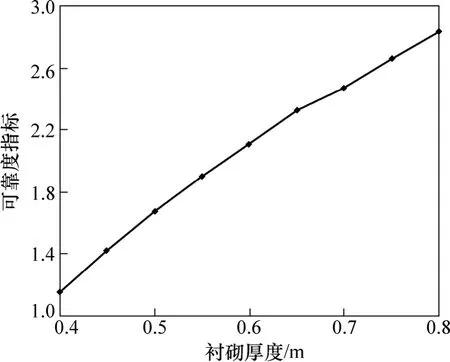
图1 衬砌厚度与可靠度指标关系曲线Fig.1 Relationship between lining thickness and reliability index

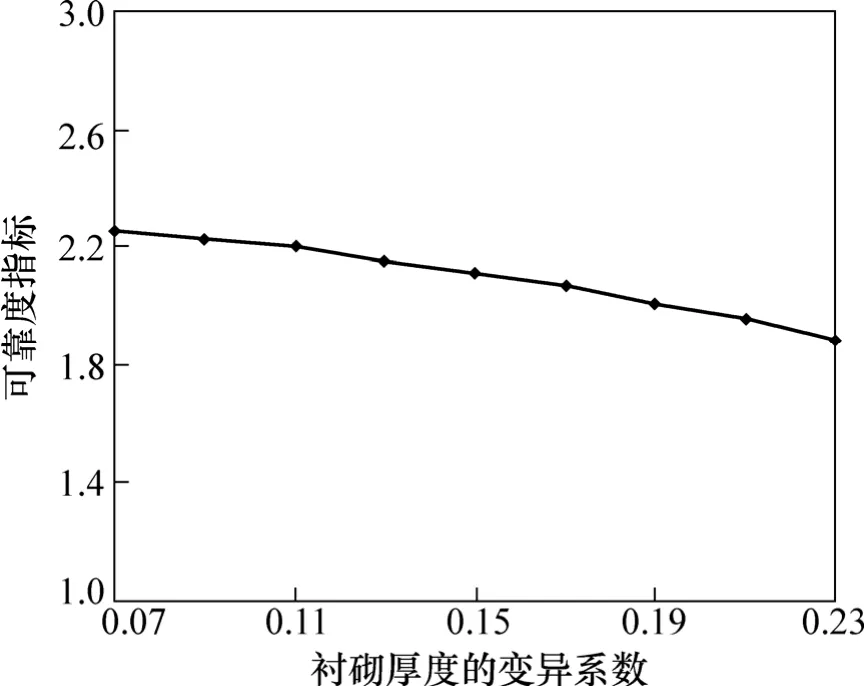
图2 衬砌厚度的变异系数与可靠度指标关系曲线Fig.2 Relationship between variation coefficient of lining thickness and reliability index

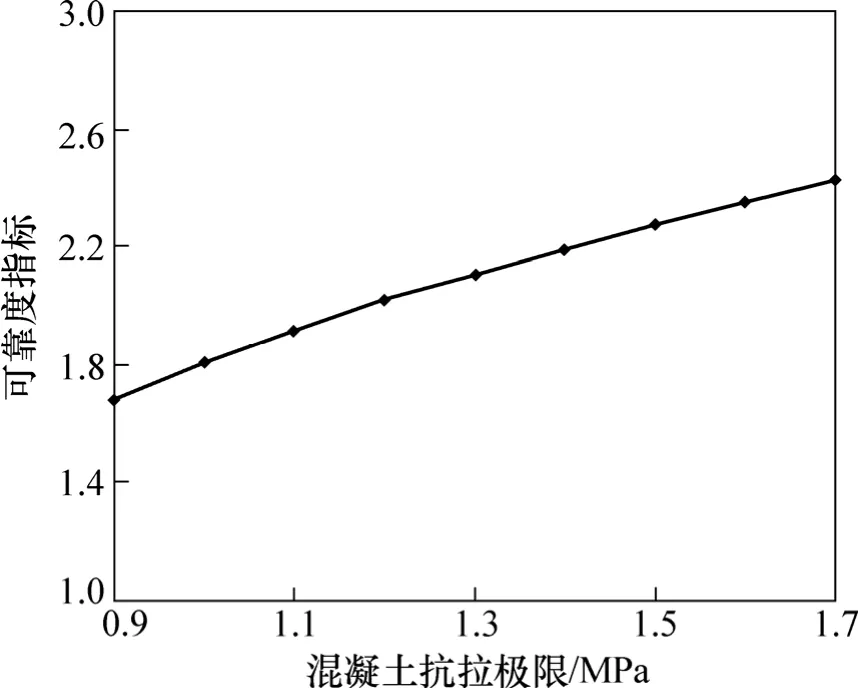
图3 混凝土抗拉极限与可靠度指标关系曲线Fig.3 Relationship between tensile ultimate stress of concrete and reliability index

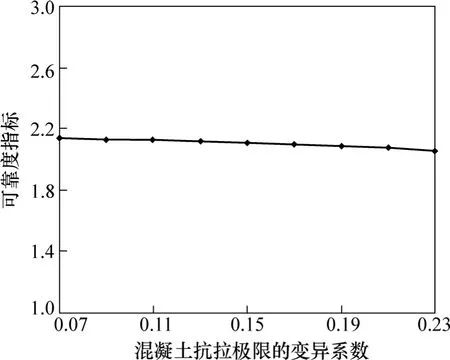
图4 混凝土抗拉极限的变异系数与可靠度指标关系曲线Fig.4 Relationship between variation coefficient of tensile ultimate stress of concrete and reliability index

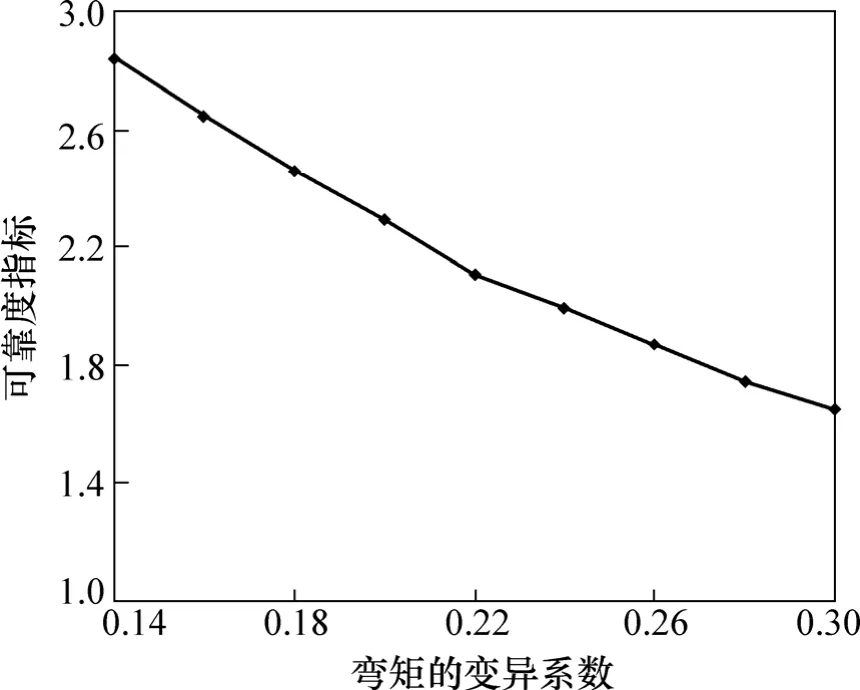
图5 弯矩的变异系数与可靠度指标关系曲线Fig.5 Relationship between variation coefficient of bending moment and reliability index

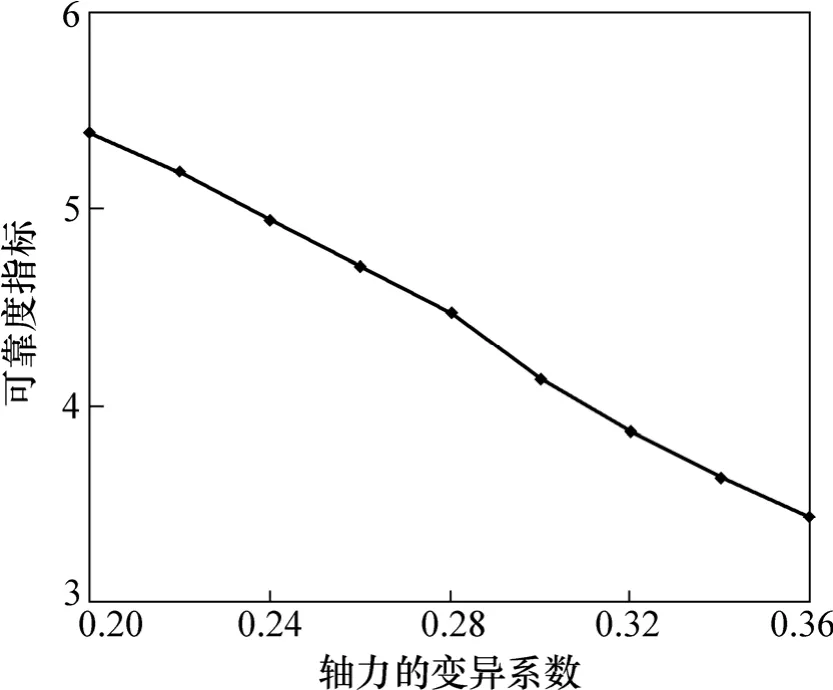
图6 轴力的变异系数与可靠度指标关系曲线Fig.6 Relationship between variation coefficient axial force and reliability index

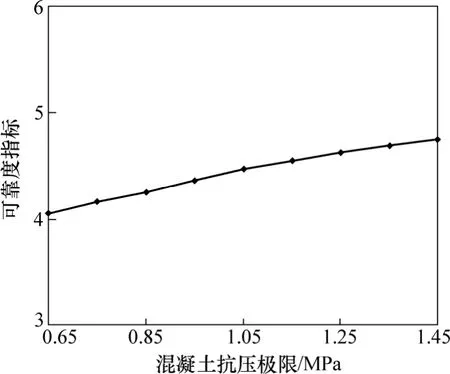
图7 混凝土抗压极限与可靠度指标关系曲线Fig.7 Relationship between pressure ultimate stress of concrete and reliability index

(3) 从图5、图6可知：弯矩和轴力的变异系数对可靠度指标的影响较大，在设计过程中，系统考虑弯矩和轴力的离散性和随机性是必要的。

5 结论

(1) 为保证隧道衬砌结构可靠度计算精度，必须从参数估计、极限状态功能函数和结构可靠度计算方法3个方面着手，任何一个方面出现较大误差都会给结果造成较大偏差。

(2) 采用基于最大熵原理的方法计算隧道衬砌结构参数的概率密度函数，并通过拟合检验确定分布的正确性，可以满足工程可靠度计算对参数的要求。

(3) Microsoft Excel规划求解器实现最优化方法计算可靠度指标不需要编程，只需要简单的Excel操作基础，即可进行可靠度计算，操作非常简便，可满足一般工程技术人员的要求。采用该方法计算隧道衬砌结构可靠度无需将状态函数线性化，不受基本变量维数限制，其收敛速度快，计算效率高，且与蒙特卡罗100万次直接抽样法计算结果比较，具有很高的精度。

(4) 提高隧道支护结构的可靠度可从以下几个方面进行：增加衬砌厚度；减小衬砌厚度的变异系数；增加混凝土抗拉、抗压极限；减小混凝土抗拉、抗压极限的变异系数。该方法还能广泛适用于交通工程、水利工程、防护工程、巷道工程等隧道及地下工程领域的可靠度计算和分析。

[1]Bucher C G, Bourgund U. A fast and efficient response surface approach for structural reliability problems[J]. Structural Safety,1990, 7(1): 57-66.

[2]Karamchandani A, Cornell A C. Sensitivity estimation within first and second order reliability methods[J]. Structural Safety,1992, 11(2): 95-107.

[3]Tichy M. First-order three-moment reliability method[J].Structural Safety, 1994, 16: 189-200.

[4]Hohenbichle M, Rackwitz R. Improvement of second-order reliability estimates by importance sampling[J]. Journal of Engineering Mechanics, ASCE, 1994, 120(1): 2195-2203.

[5]冯晓波, 杨桦. 用MATLAB实现蒙特卡罗法计算结构可靠度[J]. 中国农村水利水电, 2002(8): 50-51.FENG Xiao-bo, YANG Hua. The structural reliability calculation based on Monte-carlo and Matlab[J]. China Rural Water and Hydropower, 2002(8):50-51.

[6]朱川曲, 张道兵, 朱海燕.基于蒙特卡罗法的煤巷锚杆支护结构可靠性分析[J]. 中国安全科学学报, 2008, 18(4): 146-150.ZHU Chuan-qu, ZHANG Dao-bing, ZHU Hai-yan. Reliability analysis on bolt support structure of coal roadway based on Monte-carlo[J]. China Safety Science Journal, 2008, 18(4):146-150.

[7]张道兵, 朱川曲, 刘泽, 等. 基于 MATLAB优化工具箱的煤巷顶板锚杆支护结构可靠性分析[J]. 中国安全科学学报,2007, 17(9): 131-134.ZHANG Dao-bing, ZHU Chuan-qu, LIU Ze, et al. Reliability analysis on bolt support structure of coal roadway roof based on Matlab’s optimization toolbox[J]China Safety Science Journal,2007, 17(9): 131-134.

[8]程亮, 童玲. 最大熵原理在测量数据处理中的应用[J]. 电子测量与仪器学报, 2009, 23(1): 47-51.CHENG Liang, TONG Ling. Measurement data processing based on maximum entropy method[J]. Journal of Electronic Measurement and Instrument, 2009, 23(1): 47-51.

[9]杨杰, 胡德秀, 吴中如. 基于最大熵原理的贝叶斯不确定性反分析方法[J]. 浙江大学学报, 2006, 40(5): 810-815.YANG Jie, HU De-xiu, WU Zhong-ru. Bayesian uncertainty inverse analysis method based on pome[J]. Journal of Zhejiang University, 2006, 40(5): 810-815.

[10]丛培江, 张燕. 最大熵原理在坝体混凝土断裂韧度反演中应用[J]. 武汉理工大学学报, 2008, 30(1): 83-86.CONG Pei-jiang, ZHANG Yan. Application on maximum entropy principle in inversion analysis of fracture toughness of dam concrete[J]. Journal of Wuhan University of Technology,2008, 30(1): 83-86.

[11]谭忠盛. 隧道支护结构体系可靠度的理论研究及其工程应用[D]. 成都: 西南交通大学土木工程学院, 1998: 115-128.TAN Zhong-sheng. Theoretical research and engineering application on reliability of tunnel structure[D]. Chengdu:Southwest Jiaotong University. School of Civil Engineering,1998: 115-128.