不同受力模式下沥青混合料强度的速度特性试验研究

钱国平，刘宏富，郑健龙，李帅

(长沙理工大学 交通运输工程学院，湖南 长沙，410114)

为保证沥青路面结构在设计年限内正常工作，必须对其破坏机理进行研究。作为路面结构的一个层次，沥青混合料破坏特性应从多层体系受力方面加以分析，需要分解为各种简单的受力类型进行力学试验研究。不同试验方法测定的沥青混合料强度不同，不仅影响路面结构与材料性能评价，也会极大地影响路面结构力学计算分析结果[1]。沥青混合料是一种典型的黏弹性材料，其强度受加载速度与温度的影响显著[2-3]。目前，研究者较多地从影响沥青混合料强度的因素进行研究，对影响沥青混合料强度的内部因素(材料的组成、结构以及材料的性能)和外部因素(温度、荷载及速率)进行分析[4-12]，如：李立寒等[6]借助劈裂强度试验，探讨了泡沫沥青混合料强度增长规律及其影响因素、生产工艺条件对泡沫沥青混合料强度的影响以及泡沫沥青混合料的贮存特性；孟岩等[7]分析了纤维增强沥青混合料强度形成机理，与无纤维沥青混合料试验结果进行对比；Huang等[8-9]将半圆弯拉试验方法和间接拉伸试验方法进行对比，分析了半圆弯拉强度与间接拉伸强度的相关性。强度随加载速率的变化规律和不同受力模式下的强度比较还有待进一步研究。本文作者对不同受力模式下沥青混合料强度的速度特性试验进行研究，分析不同受力模式、不同加载速度对沥青混合料强度的影响，了解沥青路面材料在不同受力模式下的破坏原因，以便为建立沥青混合料强度理论与破坏准则奠定基础。

1 试验材料与配合比设计

选用细粒式沥青混合料AC-13C作为研究对象。原材料采用中海油泰州SBS(I-D)改性沥青和湖南株洲的玄武岩集料，其技术指标满足《沥青路面施工技术规范》(JTGF 40—2004)的技术要求。AC-13C密级配沥青混合料矿料级配见表1。通过马歇尔试验确定最佳油石比，最佳油石比及马歇尔试验结果见表2。

表1 AC-13C密级配沥青混合料矿料级配Table 1 Mineral aggregate gradation of AC-13C dense gradation asphalt mixture

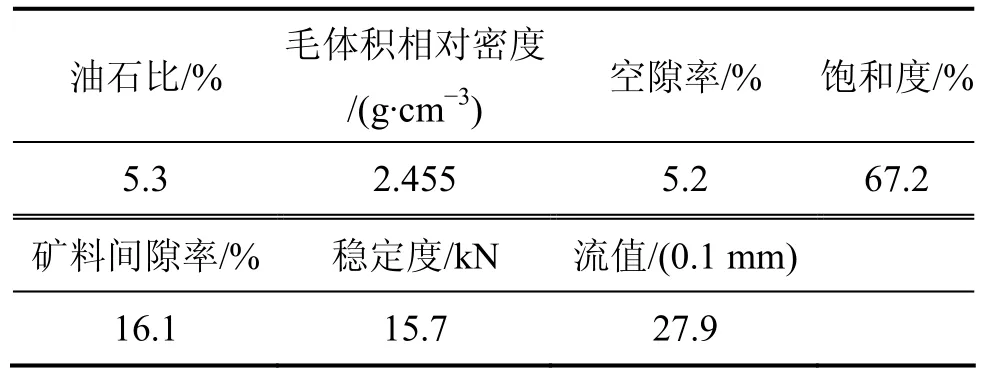
表2 最佳油石比下马歇尔试验结果Table 2 Marshall test results under optimum asphalt-aggregate ratio

2 不同受力模式下强度试验方法

采用不同受力模式下的强度试验方法，对沥青混合料的单轴抗压强度、弯曲强度、直接拉伸强度和劈裂强度进行比较。不同受力模式的强度试验采用不同的夹具在伺服液压材料试验机MTS上完成。

2.1 单轴压缩试验

抗压强度试验采用静压成型的直径为(100±2.0)mm、高度为(100±2.0) mm的圆柱体试件，试验温度为20 ℃。抗压强度计算公式为[10]：

式中：pC为试件的抗压强度，MPa；P为试件破坏时的最大荷载，N；d为试件的直径，mm。

2.2 弯曲试验

弯曲强度试验采用轮碾成型后切制的长为(250±2.0) mm、宽为(50±2.0) mm、高为(50±2.0) mm的棱柱体小梁，采用三分点加载，其跨径L为(200±0.5)mm，试验温度为20 ℃，弯曲强度计算公式为[10]：

式中：pB为弯拉强度，MPa；h和b分别为试件跨中断面的高度和宽度，mm；L为跨径，mm；PB为破坏荷载，N。

2.3 直接拉伸试验

式中：pD为试件的直接拉伸强度，MPa；a和b为试件的宽度和高度，mm。

2.4 劈裂试验

劈裂强度试验采用标准击实法成型的直径为(101.6±0.25) mm、高为(63.5±1.3) mm 的马歇尔试件，使用压条宽度为12.7 mm，试验温度为20 ℃，劈裂强度计算公式为[10]：

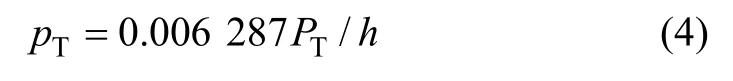
式中：pT为劈裂抗拉强度，MPa；PT为试验最大荷载，N；h为试件高度，mm。

3 不同加载速率下沥青混合料强度试验

3.1 不同加载速率下强度的试验结果

沥青混合料不同加载速率下强度试验采用应力控制方式。考虑不同受力模式下强度试验试件尺寸的影响，将加载速率换算为应力形式，不同受力模式、不同加载速率下沥青混合料强度试验结果见表3。

从表3可见：以直接拉伸强度为例，最大加载速率为37 MPa/s时的强度为5.23 MPa，是最小加载速率0.003 7 MPa/s时强度0.84 MPa的6.2倍，说明加载速度对沥青混合料的强度影响非常显著；不同受力模式下，沥青混合料强度均随加载速率的增大而增大。将表3中不同受力模式下的沥青混合料强度随加载速率的试验结果绘于双对数坐标图1中，见图1。

从图1可见：不同受力模式下的强度在双对数坐标中可近似地表示为线性关系，不同受力模式下强度随加载速率变化按线性回归的参数见表4。

由图1和表4可见：加载速率对沥青混合料强度有显著影响；不同受力模式下强度均随加载速率的增大而增大，加载速率较低时强度随速率增加较快；随着加载速率的增大，强度增加的幅度渐渐平缓，沥青混合料强度随加载速率v可近似表示为幂函数关系，且相关性较好。不同受力模式下强度随加载速率的幂函数回归方程见表4中最后1列。

厄瓜多尔矿业副部长费尔南多·贝纳尔卡萨(Fernando Benalcázar)日前在澳大利亚举办的国际采矿和资源会议上表示，政府的一大战略目标是在2021年将矿业对GDP贡献率从目前的1.55%提升至4%。

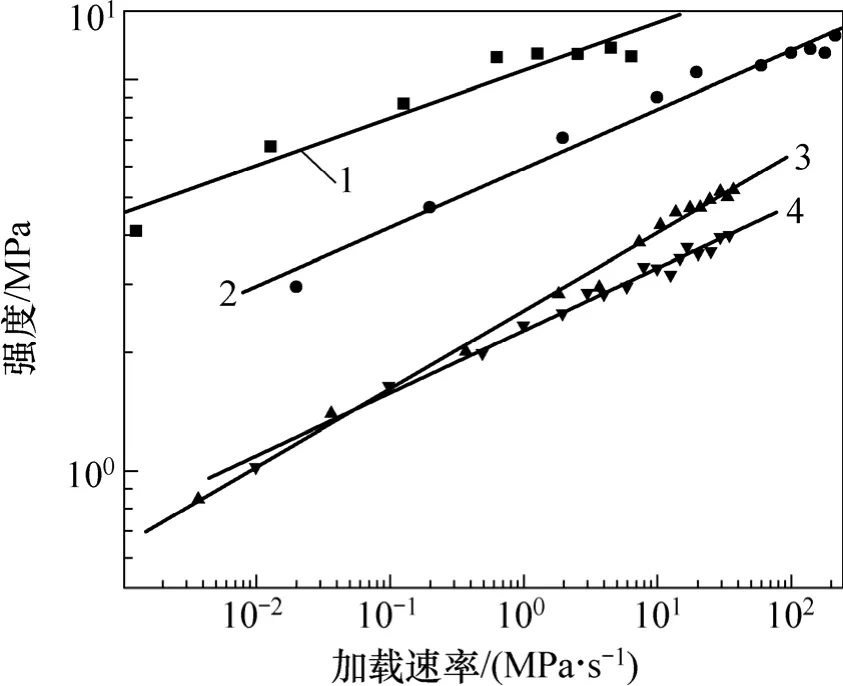
图1 不同受力模式下强度随加载速率的变化规律Fig.1 Strength variation with loading rate under different force modes

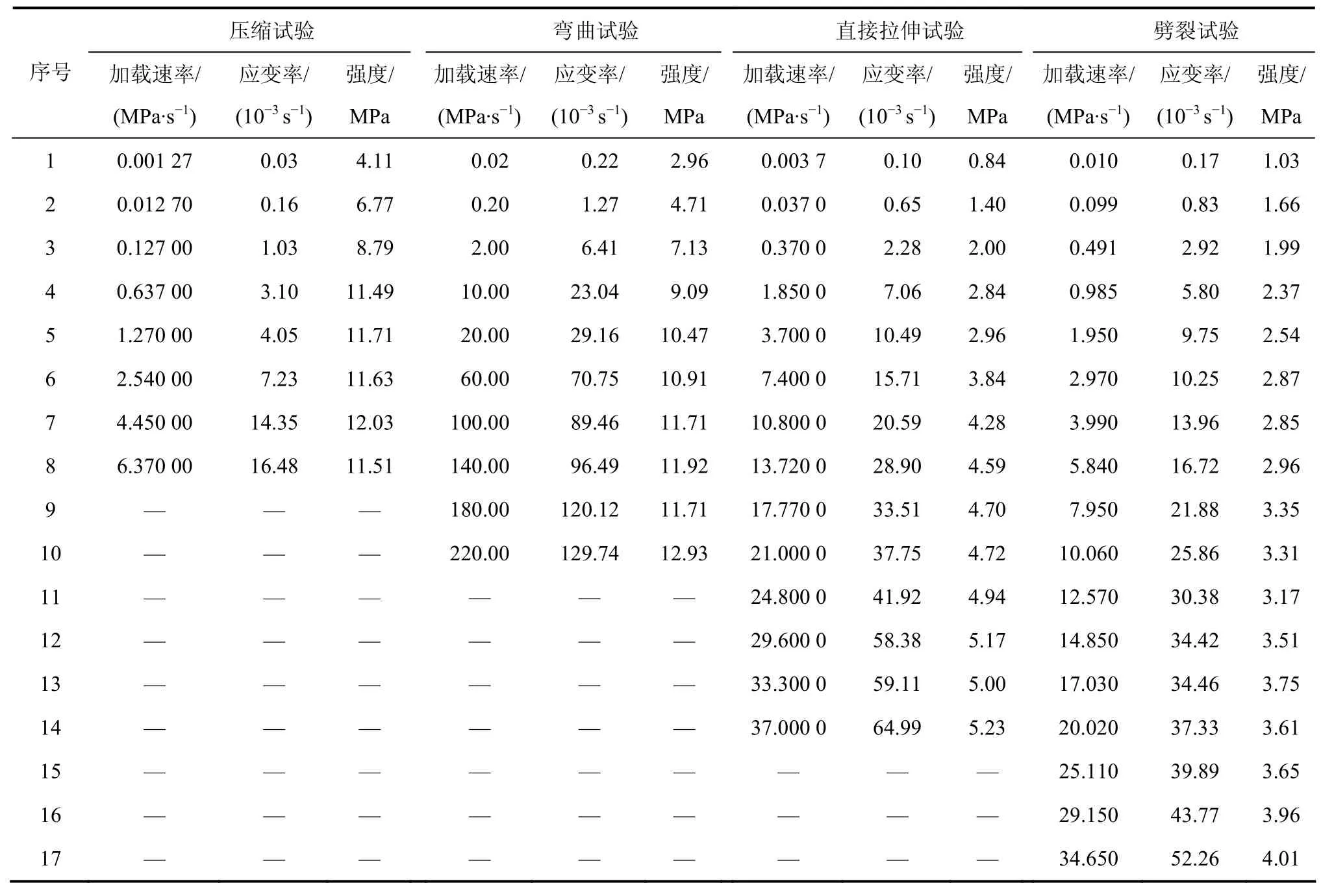
表3 不同受力模式、不同加载速率下的沥青混合料强度试验结果Table 3 Strength test results of asphalt mixture under different force modes and different loading rates

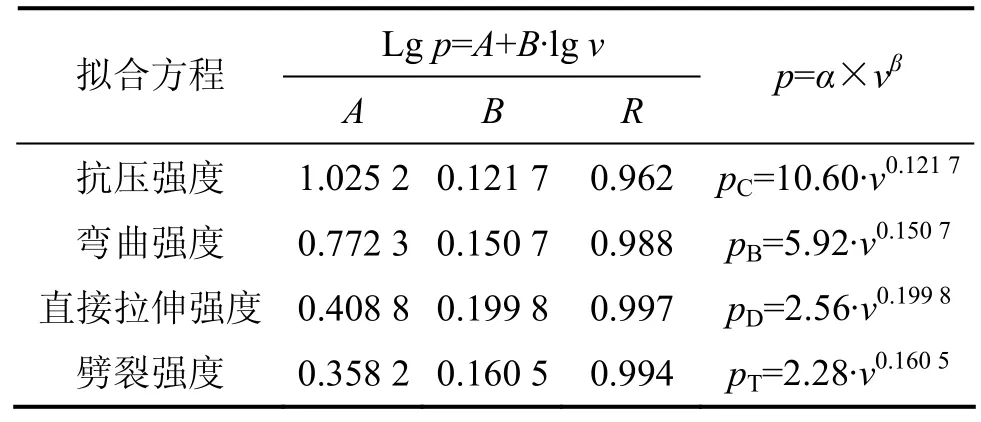
表4 不同受力模式下强度随加载速率变化的回归参数Table 4 Regression parameters of strength variation with loading rate under different force modes

3.2 不同加载速率下沥青混合料的破坏模式

沥青混合料是典型的黏弹性物质，其破坏形态受加载速率影响。在不同使用条件下，菅原提出了沥青混合料3种破坏模式：脆性破坏、柔性破坏及过渡区破坏[1]。图2所示为不同加载速率下弯拉试验、直接拉伸试验和劈裂试验的荷载-变形曲线。由于抗压试验时为了保护试验仪器，在荷载达到最大值之后就停机，荷载-变形曲线不完整，因此，没有给出单轴压缩试验的荷载-变形曲线。

由图2可见：随着加载速率的增大，荷载-变形曲线的峰值逐渐增大，定义荷载-变形曲线的峰值为破坏点，可以求得相应破坏强度，说明强度随加载速率的增大而逐渐增大，当加载速率较高时，如弯曲试验和直接拉伸试验加载速率100 kN/s、劈裂试验加载速率为400 kN/s时，荷载-变形近似呈线性关系，沥青混合料呈脆性破坏，破坏表现为突然的破断(如弯曲和直接拉伸强度)或崩裂(如劈裂强度)，一到破坏点立即丧失承载能力，破坏断面中往往可见粗集料的断裂破坏；当加载速率较低，如弯拉试验的加载速率为10 N/s、直接拉伸和劈裂试验的加载速率为0.1 N/s时，荷载-变形关系呈曲线形式，沥青混合料发生流动变形时的柔性破坏，荷载达到最大值时，试件已明显产生裂缝，实际上已经破坏。荷载-变形曲线过峰值后，试件仍有一定的承载能力，破坏方式以微裂缝的形式存在;当加载速率由高向低变化时，沥青混合料的破坏形式逐渐由脆性破坏向柔性破坏过渡；介于脆性破坏和柔性破坏二者之间的为过渡区破坏模式。荷载-变形曲线在保持一段直线关系后在接近峰值时产生类似于屈服点的转折或微小曲线，过了峰值后，即使并非马上断裂也只能维持极短时间而破断。通过以上3种受力模式下不同加载速率的沥青混合料强度试验结果验证了菅原所提出的破坏模式。

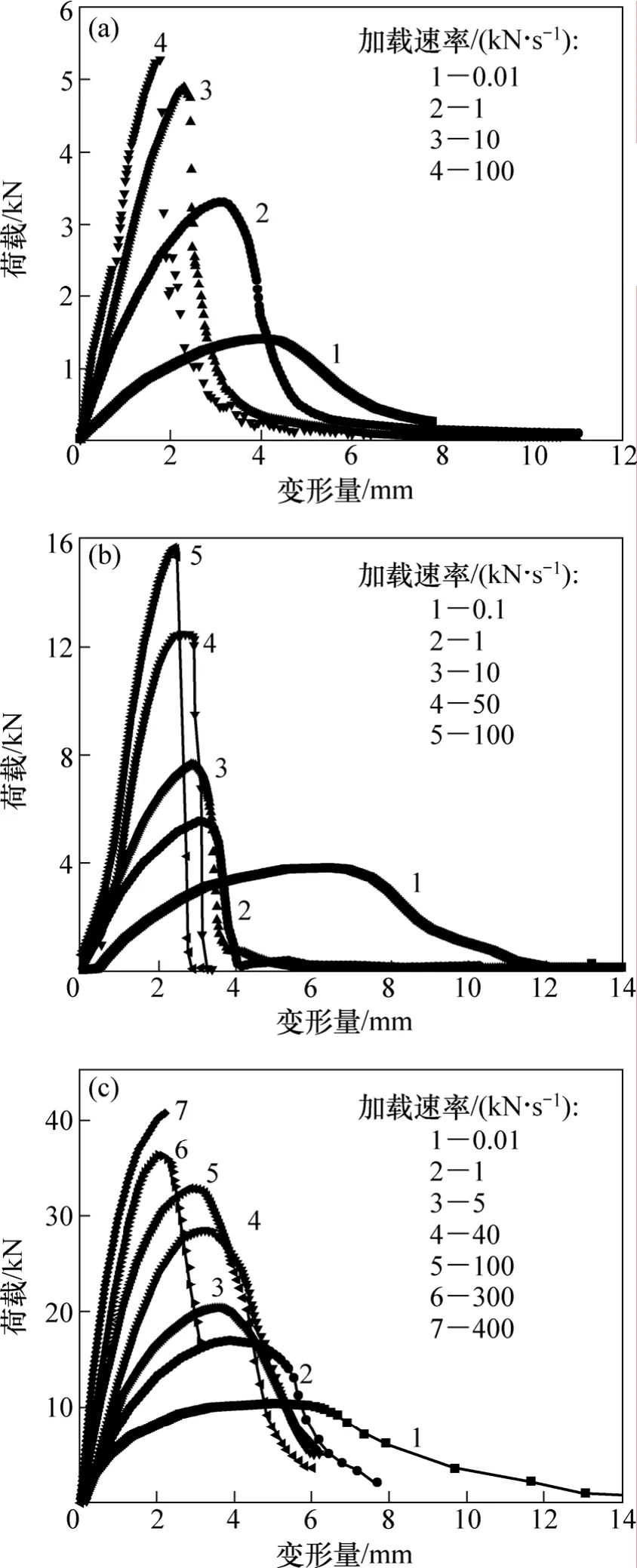
图2 不同加载速率下强度试验的荷载-变形曲线Fig.2 Load-deformation curves of strength test under different load rates

3.3 强度参数随加载速率的变化规律

根据沥青混合料的颗粒性特征，其强度构成来源于2个方面：由于沥青存在而产生的黏结力和由于集料存在而产生的内摩阻力。普遍采用摩尔-库仑理论作为分析沥青混合料的强度理论，参数黏结力c和内摩阻角φ作为强度理论的分析指标。摩尔-库仑的理论表达式为[1]：

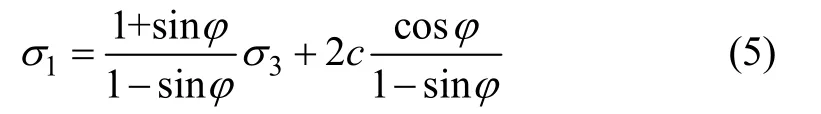
沥青混合料强度参数黏结力c和内摩阻角φ可通过测定无侧限抗压强度和抗拉强度予以换算。当无侧限抗压时，相当于σ1=pC及σ3=0，代入式(5)得：

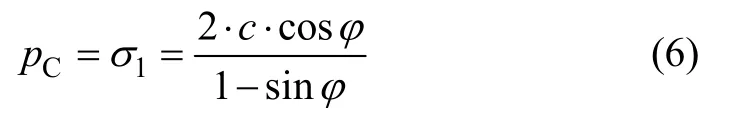
当直接拉伸时，相当于σ1=0及-σ3=pD，

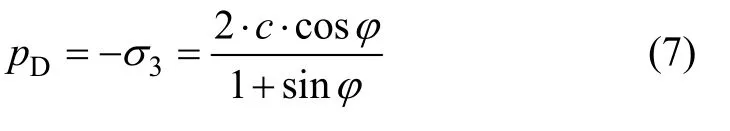
联立式(6)和式(7)得：

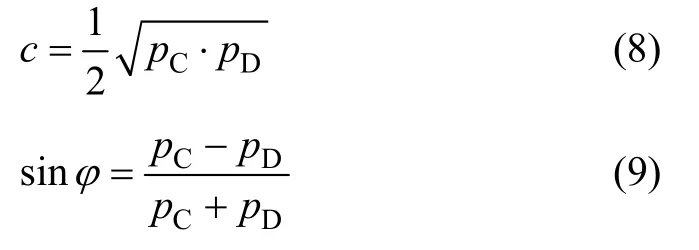
通过进行单轴压缩试验和直接拉伸试验获得不同加载速率下的抗压强度和抗拉强度，应用式(8)和式(9)计算不同加载速率下的沥青混合料内摩擦角φ和黏聚力c，所得不同加载速率下强度参数结果见表5。沥青混合料内摩擦角和黏聚力随加载速率的变化规律见图3。

由图3可见：沥青混合料黏聚力随加载速率增大先急剧增大而后趋于平稳；内摩擦角随加载速率变化规律正好与黏聚力变化规律相反，先急剧减小而后趋于平稳。黏聚力和内摩擦角随加载速率变化的原因可能是较高的加载速率对应较短的加载时间，沥青混合料将发生脆性破坏；较低的加载速率对应较长的加载时间，沥青混合料呈现流动变形破坏。当呈现流动变形破坏时，沥青混合料的黏聚力减小，强度主要由内摩擦阻力提供；随着加载速率的增大，破坏模式逐渐向脆性破坏过渡，黏聚力逐渐增大，内摩擦阻力逐渐减小。

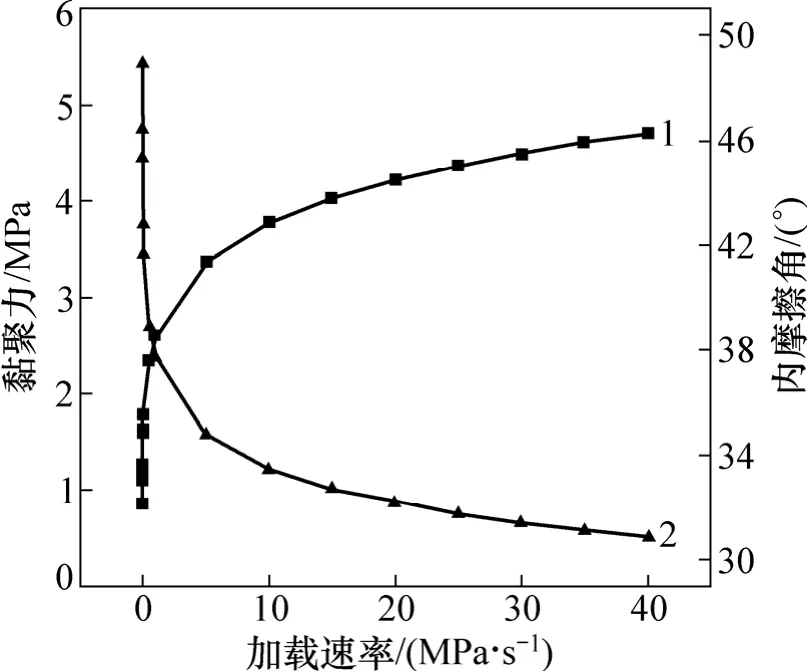
图3 内摩擦角和黏聚力随加载速率变化规律Fig.3 Internal friction angle and cohesion of asphalt mixtures under different load rates

4 不同受力模式下沥青混合料强度对比分析

4.1 不同受力模式下沥青混合料强度对比

不同受力模式下沥青混合料的强度比较应基于相同的应变速率进行[13-14]，根据表3中的试验结果，得出不同受力模式下应变率与强度的关系，如图4所示。

强度随应变率变化在双对数坐标中呈线性关系，用下列方程进行拟合：

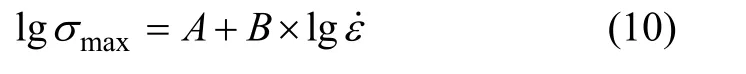
式中：σmax为混合料的强度；ε˙为应变率；A和B为拟合参数。

不同受力模式下的拟合结果见表6。由图4可知：在相同应变率条件下，沥青混合料的强度受加载方式的影响，不同受力模式下的强度由大至小依次为抗压强度、弯拉强度、直接拉伸强度和劈裂强度；随着应变率的增加，不同受力模式下的沥青混合料强度均增大，两者在双对数坐标中呈线性关系，这意味着只有当应变率发生量级变化时，才会对强度有显著影响。斜率B反映了强度随应变率的敏感程度，直接拉伸试验的B最大，说明直接拉伸强度随应变率变化最敏感。

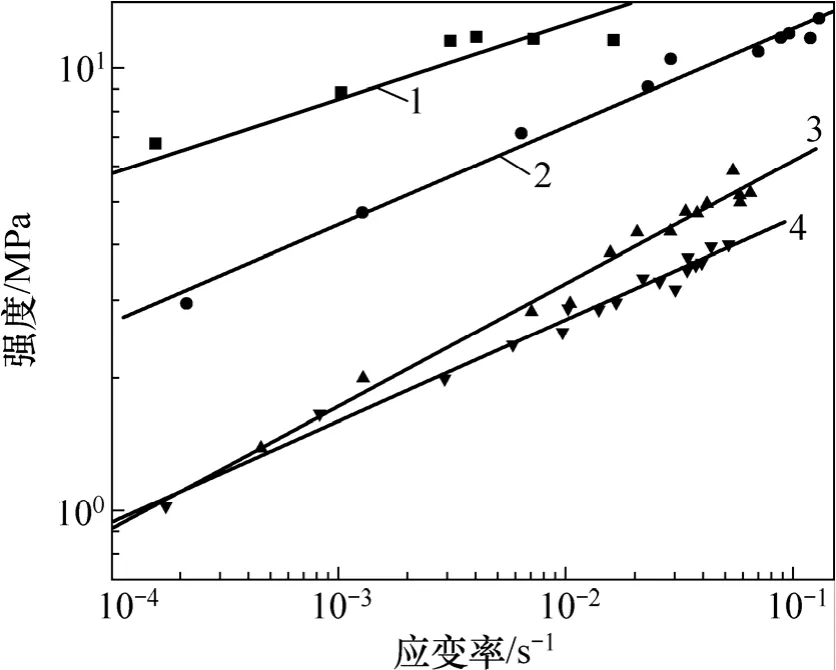
图4 不同受力模式强度随应变率变化规律Fig.4 Variation of strength with strain rate under different force modes

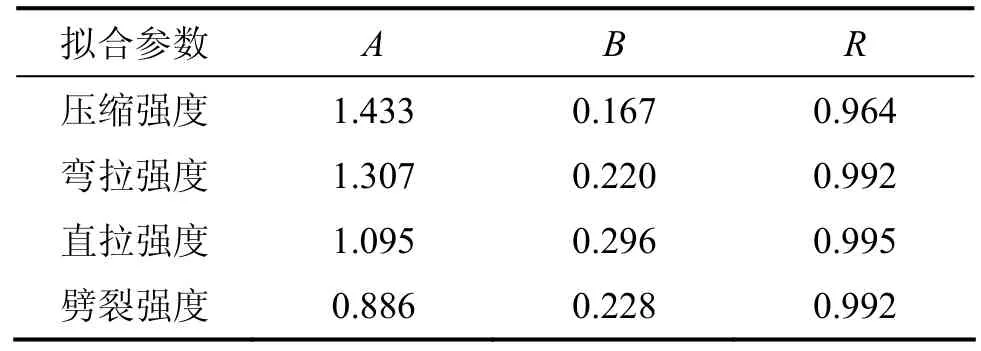
表6 强度随应变率变化线性拟合结果Table 6 Linear fitting results of changes in strength with strain rate

4.2 不同受力模式下强度的比较分析

不同试验方式的力学原理不同，在无侧限抗压试验条件下，沥青混合料试件承受压应力，集料颗粒相互靠近，抗压强度主要取决于由集料颗粒所形成的内摩阻力和嵌挤力，由于内摩阻力和嵌挤力远大于黏结力，所以，抗压强度大于其他3种受力模式下的强度；由于内摩阻力和嵌挤力主要是由集料形成的，集料受应变率的影响较小，所以，抗压强度随应变率变化不敏感，抗压强度的B最小。

在直接拉伸试验条件下，集料之间填充的胶结料发挥良好的黏结作用，抗拉强度主要取决于沥青胶浆、沥青与矿料间的黏结力，所以，4种受力模式中直接拉伸强度最小。由于这种黏结力主要是由沥青胶结料形成的，沥青胶结料是一种黏弹性物质，其对应变率较敏感，直接拉伸试验强度随应变率的B最大。

在三点弯拉试验条件下，小梁内部形成拉应力区和压应力区，压应力主要由骨架所形成的内摩阻力和嵌挤力承受，拉应力主要由沥青胶浆、沥青与矿料间的黏结力承受，弯拉强度间于抗压强度和直接拉伸强度之间，弯拉试验的B也介于抗压强度和直接拉伸强度试验的B之间。劈裂试验即间接拉伸试验，劈裂试验试件沿着加载方向，中部产生拉应力，两端产生的是压应力，劈裂强度及随应变率的敏感性均与直接拉伸试验结果很接近。

5 结论

(1) 加载速率对沥青混合料强度有显著影响，不同受力模式下强度均随加载速率的增大而增大，强度随加载速率v可近似表示为幂函数关系。

(2) 沥青混合料黏聚力c随加载速率增大先急剧增大而后趋于平稳，内摩擦角φ随加载速率变化规律正好与黏聚力规律相反，先急剧减小而后趋于平稳；较高的加载速率沥青混合料呈脆性破坏；较低的加载速率沥青混合料呈现柔性破坏。

(3) 在相同应变率条件下，沥青混合料强度受加载方式的影响，其影响程度由大至小依次为抗压强度、弯拉强度、直拉强度和劈裂强度，并从沥青混合料结构组成对不同受力模式下强度差异进行了解释。

[1]沈金安. 沥青及沥青混合料路用性能[M]. 北京: 人民交通出版社, 2001: 267-315.SHEN Jin-an. Pavement performance of asphalt and asphalt mixtures[M]. Beijing: China Communications Press, 2001:267-315.

[2]张肖宁. 沥青与沥青混合料的黏弹性原理及应用[M]. 北京:人民交通出版社, 2006: 175-195.ZHANG Xiao-ning. Viscoelastic principle and application of asphalt and asphalt mixtures[M]. Beijing: China Communications Press, 2006: 175-195.

[3]刘立新. 沥青混合料黏弹性力学及材料学原理[M]. 北京: 人民交通出版社, 2006: 136-152.LIU Li-xin. Viscoelastic mechanics and materials science principle of asphalt mixtures[M]. Beijing: China Communications Press, 2006: 136-152.

[4]Sadd M H, Dai Q L, Parameswaran V, et al. Microstructural simulation of asphalt materials: Modeling and experimental studies[J]. Journal of Materials in Civil Engineering, American Society of Civil Engineers, 2004, 16(2): 140-146.

[5]Roque R, Zhang Z, Sankar B. Determination of crack growth rate parameters of asphalt mixtures using the Superpave IDT[J].Assoc Asphalt Paving Technology, 1999, 68(3): 404-433.

[6]李立寒, 王太鑫, 袁坤. 泡沫沥青稳定碎石混合料强度特征的试验研究[J]. 建筑材料学报, 2009, 12(5): 549-554.LI Li-han, WANG Tai-xin, YUAN Kun. Study on strength characteristics of foamed asphalt mixture[J]. Journal of Building Materials, 2009, 12(5): 549-554.

[7]孟岩, 梅迎军, 李志勇, 等. 纤维沥青混合料试验性能研究[J].重庆交通大学学报: 自然科学版, 2007, 26(6): 110-116.MENG Yan, MEI Ying-jun, LI Zhi-yong, et al. Study on testing performance of fiber reinforced asphalt mixture[J]. Journal of Chongqing Jiaotong University: Natural Science, 2007, 26(6):110-116.

[8]Huang B, Shu S, Tang Y. Comparison of semi-circular bending and indirect tensile strength tests for HMA mixtures[J].Advances in Pavement Engineering, 2005, 22(8): 1-11.

[9]刘宇, 张肖宁. 沥青混合料半圆弯拉强度与间接拉伸强度对比分析[J]. 公路交通技术, 2011, 27(3): 34-39.LIU Yu, ZHANG Xiao-ning. Comparative analysis for semicircle bending strength and indirect tensile strength of asphalt mixtures[J]. Technology of Highway and Transport, 2011,27(3): 34-39.

[10]JTJ 052—2000, 公路工程沥青及沥青混合料试验规程[S].JTJ 052—2000, Standard test methods of bitumen and bituminous mixtures for highway engineering[S].

[11]赵永利. 沥青混合料的结构组成机理研究[D]. 南京: 东南大学交通运输学院, 2005: 56-76.ZHAO Yong-li. Composition mechanism of asphalt mixtures[D].Nanjing: Southeast University. School of Traffic and Transportation, 2005: 56-76.

[12]王海龙, 李庆斌. 不同加载速率下饱和混凝土的劈拉试验研究及强度变化机理[J]. 工程力学, 2007, 24(2): 105-110.WANG Hai-long, LI Qing-bin. Experiments on saturated concrete under different splitting tensile rates and mechanisms on strength change[J]. Engineering Mechanics, 2007, 24(2):105-110.

[13]Cadoni E, Labibes K, Albertini C. Strain-rate effect on the tensile behavior of concrete at different relative humidity levels[J].Materials and Structures, 2001, 34(5): 21-26.

[14]ZHENG Dan, LI Qing-bin. An explanation for rate effect of concrete strength based on fracture toughness including free water viscosity[J]. Engineering Fracture Mechanics, 2004, 71(2):2319-2327.