脆性岩石全应力应变过程中渗透性突变研究

姜春露，孙强 ，姜振泉, ，朱术云

(1. 中国矿业大学 资源与地球科学学院，江苏 徐州，221116；2. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州，221008；3. 中国科学院 地质与地球物理研究所工程地质力学重点实验室，北京，100029)

矿山井巷、地下厂房及地下核废料储存硐室等地下工程防渗涉及扰动岩体渗透性问题。工程开挖对岩体结构的扰动必然会导致其渗透性的变化，二者具有密切的关联性，然而，由于岩体结构与渗透性对应关系复杂，要直接建立二者的量化关系模型存在极大的技术难度。为此，国内许多学者采用岩石全应力-应变过程的渗透试验，通过岩石全应力-应变过程的应力-渗透性或应变-渗透性关系揭示其渗透性与内部结构的关系特征。李世平等[1]对江苏徐州矿区殷庄砂岩在全应力-应变过程中的渗透性进行了研究，并提出岩石的渗透性与应力、应变有较强的函数关系。彭苏萍等[2-3]通过试验研究了沉积岩变形破坏过程中渗透率变化及围压对砂岩渗透率变化的影响规律，建立了砂岩岩石应力-应变与渗透率之间的定性定量关系。姜振泉等[4-5]对软、硬岩进行了不同应力条件的全应力-应变过程渗透性对比试验，提出了临界抗渗强度和起始渗透率 2个特征值。朱珍德等[6]研究了脆性岩石全应力应变过程中渗透特性。韩宝平等[7-11]进行了伺服渗透试验，从不同角度研究了岩石全应力应变过程中渗透性变化。多数学者研究得出渗透性增强的过程中存在一明显的突变点，该点前后渗透性差异较明显，反映在渗透率-应力曲线上，该突变点前后曲线斜率发生较明显的变化。然而，受岩石非均质性、试验样本数、试验过程中数据采集间隔等多种因素影响，相关学者在各自的试验分析中没有给出突变点处应力与峰值应力之间的量化表达式。为此，本文作者在分析脆性岩石全应力应变过程中渗透性演化的基础上，结合岩石统计强度理论，利用重整化群理论推导出该突变点对应的应力与峰值应力比值的数学表达式，利用伺服渗透试验数据和其他文献结果，验证该表达式的合理性。

1 岩石变形破坏过程中渗透性变化

伺服渗透试验结果[1-12]表明脆性岩石在全应力应变过程中渗透率变化的总体规律是：在加载初期，渗透率随应力的增大而略有降低(原生微裂隙闭合)或渗透率变化不大(原生微裂隙不发育)；随着轴向应力的增加，岩石在外载荷与孔隙压力联合作用下，内部结构出现微裂隙萌生和原始孔隙扩展，渗透率缓慢增加；随着岩石轴向应力的继续增加，岩石内部结构的微裂纹合并，逐渐演变成宏观裂缝，岩石出现破裂，渗透率剧增；岩石宏观破裂之后，岩块沿断裂面产生错动和凹凸体的爬坡效应，使宏观裂隙法向间距加大，渗透率也达到峰值；随着破裂岩块变形的进一步发展，

凹凸体被剪断或磨损，裂隙间距减小，同时，剪切与磨损产生的岩屑部分充填到裂隙间，破裂岩石的渗透性下降，如图1所示。其中：σm为临界抗渗强度；K为渗透率；ε为应变；σ为轴向应力。

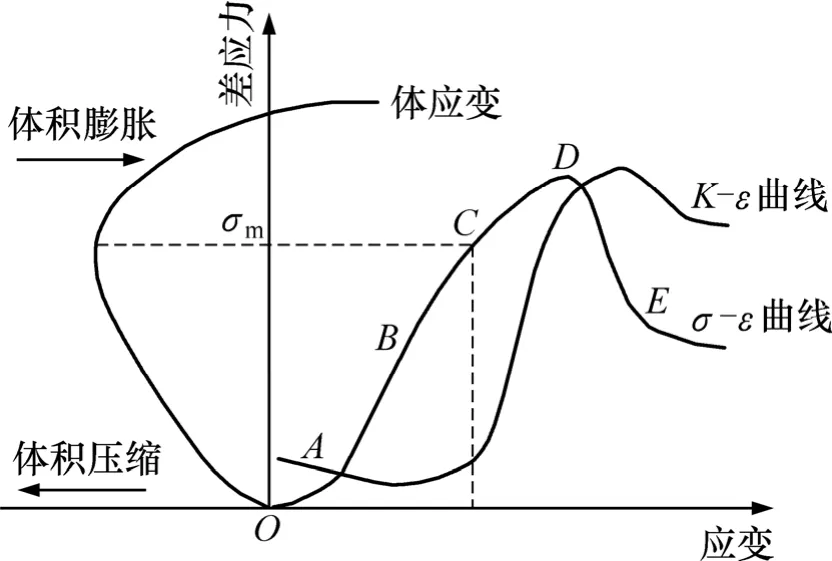
图1 脆性岩石全应力应变过程中渗透性演化Fig.1 Permeability evolution of brittle rock during full stress-strain process

姜振泉等[4-5]发现岩石破坏前渗透率-应力关系的共同特点是：在较低的应力水平时，渗透性略微下降，而后渗透性随应力提高而增强。在渗透性增强过程中存在1个明显的突变点，其前后渗透性差异较明显，反映在渗透率-应力曲线上，该突变点前后曲线斜率发生较明显变化，之后的渗透率-应力近似呈线性关系。基于此，提出岩石临界抗渗强度(σm)的概念，即导致岩石开始形成裂隙性渗流的临界压力，并将其作为表征导致岩石渗流突变的应力条件的量化参数。

刘洪磊等[12]指出：试件破坏时，裂隙不断地相互贯通、扩展，体积应变开始增加，渗透率出现阶跃；当应力达到峰值时，试件内部裂隙在水力作用下加速扩展、贯通，致使试件内部裂隙完全贯通、宏观破坏，体积应变急剧增加，渗透率也迅速增大到极大值。应力轴向应变、渗透率轴向应变变化趋势及体应变-轴向应变变化趋势在拐点处基本一致。

仵彦卿[13]等利用CT方法研究得出硬岩加载过程中裂纹发育规律：加载至强度的62%之前，小裂纹非常缓慢地增加；加载至强度的 64.5%过程对应小裂纹的闭合阶段，宏观应力应变曲线的斜率也变小；之后，小裂纹进入快速发展过程直至宏观裂纹出现，此时应力为强度的79%。

将压缩条件下岩石或类岩石材料的变形与破坏过程划分为不同阶段，如图1 所示(和分别对应压密、弹性、稳定破裂、非稳定破裂、宏观破坏阶段)，对应于体膨胀界限的C点是稳定与不稳定破坏的分界点，也是临界破坏点，该点以后应变速率将远高于之前的应变速率。在阶段，即使施加的偏应力保持不变，破裂仍会累进性发展直至最终被破坏[14-15]。

综合分析上述研究结果得出，图1中临界破坏强度与临界抗渗强度(σm)对应的点为同一点C，当应力达到该值时，岩石体积由压缩向膨胀转变，内部结构出现了质的变化，贯通性渗流通道基本形成，岩石渗透性在此点前后将发生显著性变化。因此，临界破坏强度和临界抗渗强度实际上是处于同一应力水平，如果能够确定临界破坏强度，则临界抗渗强度也可以确定。

2 理论分析

由于复杂的成岩地质环境和漫长的地质改造作用，岩石内部不可避免地存在着许多宽度不一、形状各异的缺陷和损伤(如各种宽度不等的孔隙和微裂隙等)。这些缺陷和损伤在岩石内部分布不均匀，是随机的，岩石细观强度受此影响也表现出明显的非均匀性和离散性特征，因此，可以采用统计方法来描述岩石细观强度。

用经典的 Weibull分布[16]表示一个单元的破坏强度σf小于应力ασ的概率Pα，可表示为：

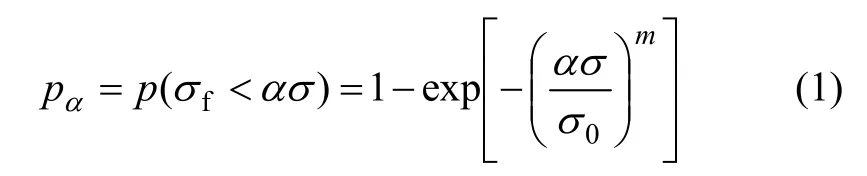
式中：pα为单元破坏强度σf小于应力ασ时的破坏概率；σ0为单元平均强度；α为尺度参数，α=1则表示为微元体；σ为单元应力；σ0为微元体统计平均应力；m表示形状参数，其值越大，表明材料越均匀，微元体之间强度离散性越小。

令α=1，则微元体破坏概率可表示为：

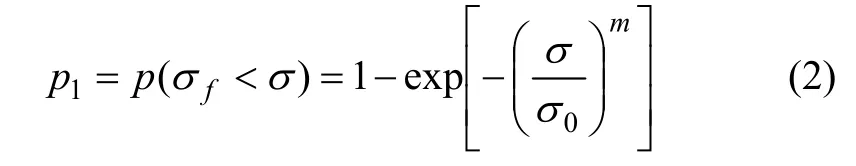
联合式(1)和式(2)，可得：

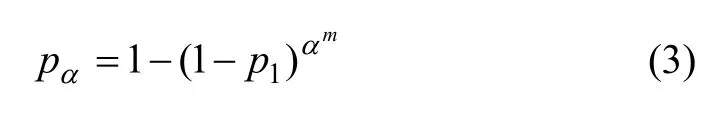
在岩石材料的加载过程中，单元很难保持相互独立，单元的破坏必将影响临近单元的应力状态，也就是说，未破坏单元要另外承受从临近破坏单元转移过来的应力。当应力(a-b)σ传递给 1个承担应力为bσ的未破坏块体时，其破坏将发生的条件概率Pa,b[17-18]可表示为：

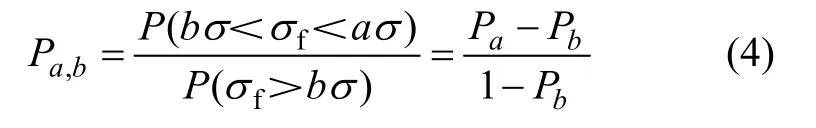
利用重整化群理论[19-21]可以得出：

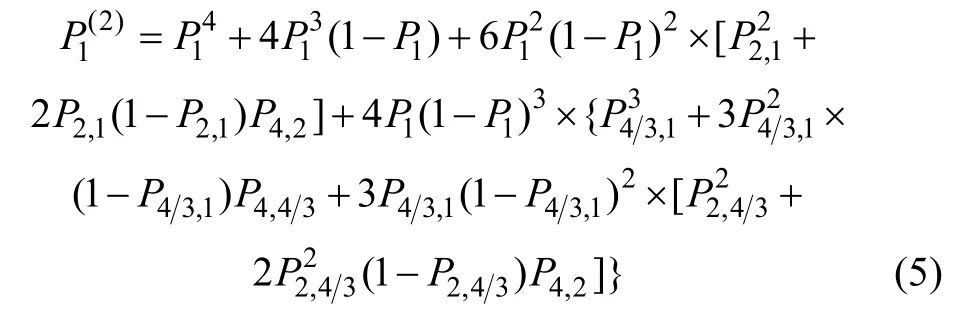
根据式(3)～(5)，利用数值迭代方法求得系统临界破坏概率P*=f(m)，如表1所示[21]。从表1可见：岩石破坏概率f(m)随形状参数m的增大而减小。

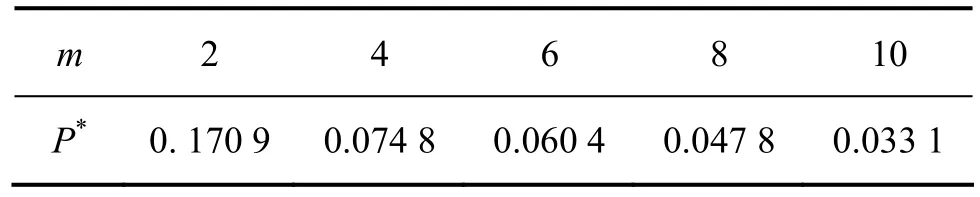
表1 临界破坏概率P*与形状参数m取值Table 1 Probability of critical failure and shape parameters

脆性岩石试样承载能力概率函数可用下式描述：

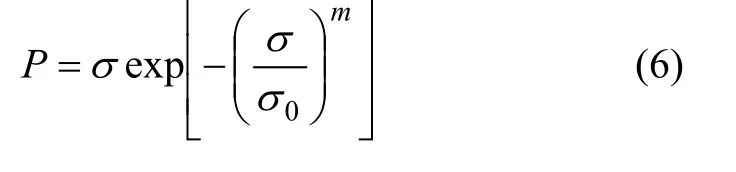
对式(6)中σ求一阶导数并令其等于0，得出试样峰值强度表达式：

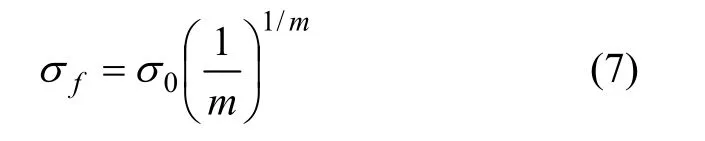
由P*=f(m)和式(1)可得临界破坏点C所对应的应力为：

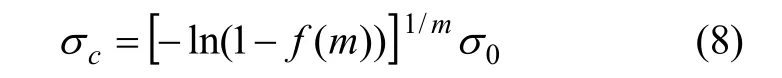
由式(7)和(8)可得：

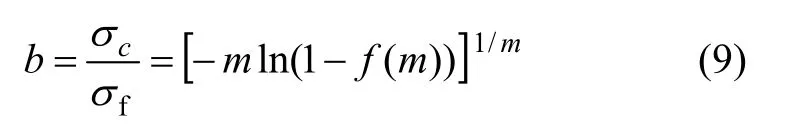
其中，m取值与围岩有关[22]，即：

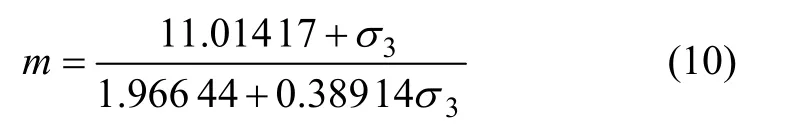
由式(9)和(10)可知：脆性岩石临界破坏点所对应的应力与峰值应力的比值b依赖于形状参数m，而m取决于围压。图2所示为围压与b的关系曲线。

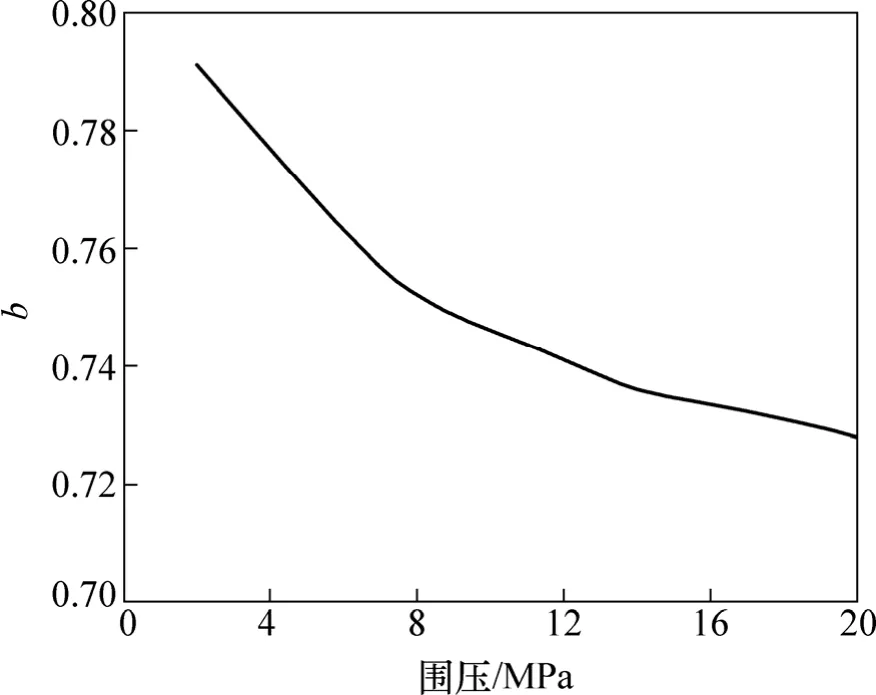
图2 b随围压变化关系Fig.2 Relationship between b and confining pressure

3 实例验证

3.1 试验分析

利用MTS815岩石力学电液伺服试验机进行伺服渗透试验[4-5]，所用岩样取自兖州矿区某矿7煤底板，试验条件如下：渗透压差为 1.5～1.8 MPa，围压为 4 MPa，孔-围压比为 0.4～0.5，试验过程控制测点为12～14个。脆性岩石全应力应变过程中渗透性变化曲线如图3所示。图中空心箭头指示利用式(9)预测的渗透性发生突变的位置，实心箭头指示试验过程中渗透性实际发生突变的位置。由图3可以看出：中砂岩、细砂岩以及灰岩样预测的渗透性突变点位置与试验过程中实际渗透性突变位置非常接近，说明式(9)被用来预测脆性岩石变形破坏过程中渗透性的突变是合理的。

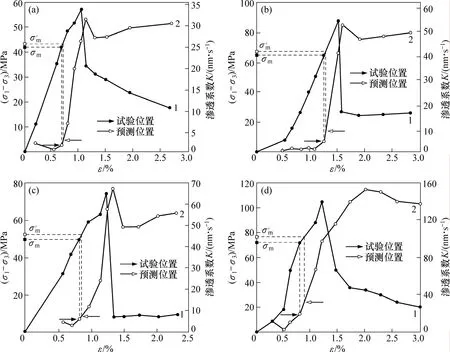
图3 脆性岩石试样全应力-应变过程的渗透性变化曲线Fig.3 Permeability-strain behavior of hard rock specimens

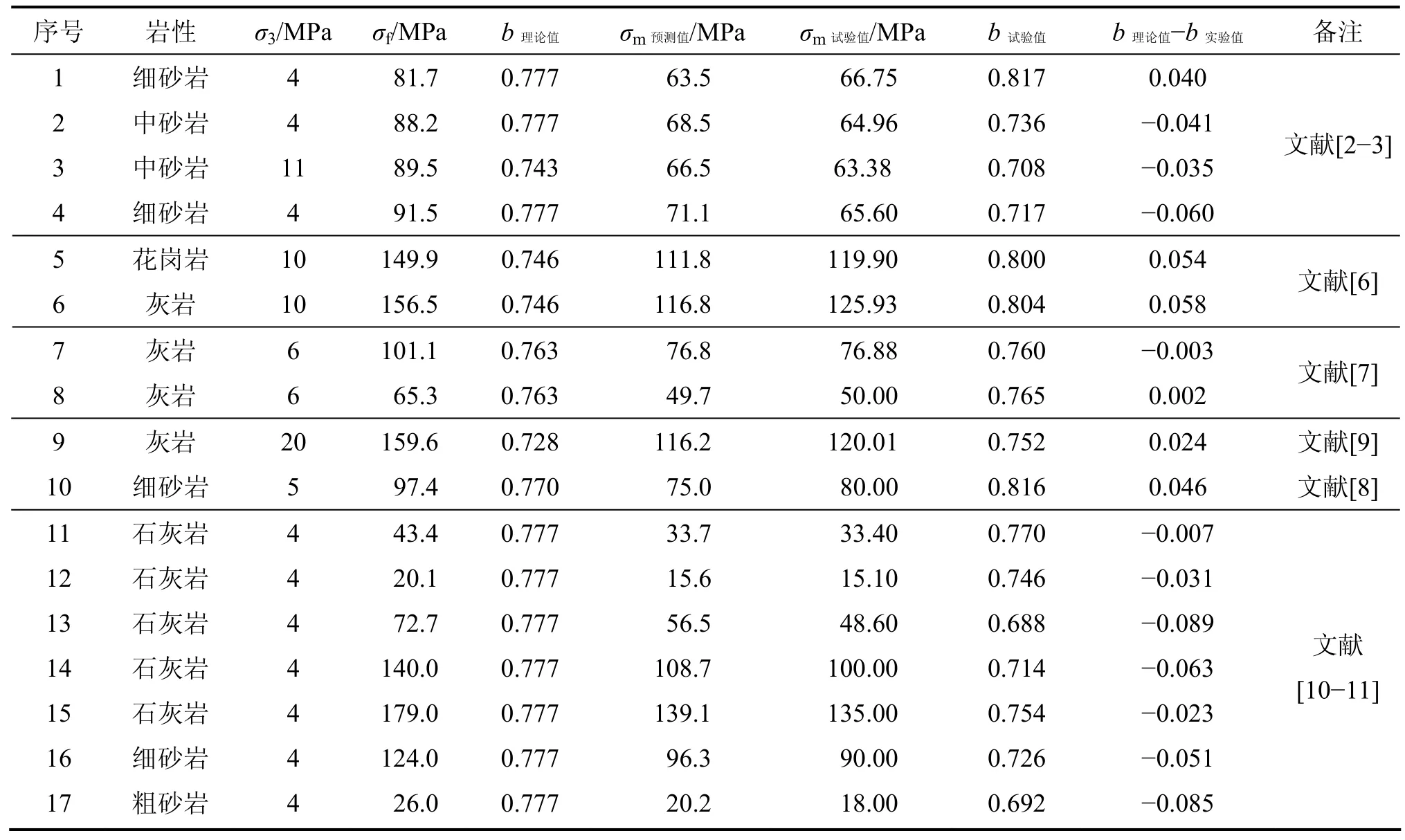
表2 试样预测值与试验值对比结果Table 2 Results of predict value and experimental

3.2 相关试验结果分析

利用式(9)对伺服渗透试验[2-3,6-11]中脆性岩石临界抗渗强度以及渗透性突变点位置进行预测，结果如表2所示。从表2可以看出：大多数岩样全应力应变试验过程中临界抗渗强度的预测值与试验值较吻合，误差在-0.089～0.058之间，从而也验证了本文提出的模型公式的合理性。由于伺服渗透试验过程中数据采集点数的限制，虽然K-ε曲线大体上描绘出脆性岩石全应力应变过程中渗透率的演化规律，但是，曲线上的某些关键点(如渗透率最低点、突变点以及最高点)可能与实际点有些差别，因此，上述误差是允许的。

4 结论

(1) 通过分析全应力应变过程中脆性岩石渗透性演化规律，得出渗透性变化过程中突变点处的应力即临界抗渗强度对应于应力-应变曲线上稳定破裂与非稳定破裂的临界点，也对应于体应变由压缩到膨胀的转变点。

(2) 基于岩石统计强度，借助重整化群理论推导出临界抗渗强度与峰值应力比值的表达式，该比值随围压增大而减小。用此表达式来预测伺服渗透试验中渗透性突变点位置，结果表明大多数脆性岩样预测值与试验值相吻合，误差在-0.089～0.058之间，平均误差为-0.016，证明了该表达式的合理性。

[1]李世平, 李玉寿, 吴振业. 岩石全应力应变过程对应的渗透率-应变方程[J]. 岩土工程学报, 1995, 17(2): 13-19.LI Shi-ping, LI Yu-shou, WU Zhen-ye. The permeability-strain equations relating to complete stress-strain path of the rock[J].Chinese Journal of Geotechnical Engineering, 1995, 17(2):13-19.

[2]彭苏萍, 屈洪亮, 罗立平, 等. 沉积岩石全应力应变过程的渗透性试验研究[J]. 煤炭学报, 2000, 25(2): 113-116.PENG Su-ping, QU Hong-liang, LUO Li-ping, et al. An experimental study on the penetrability of sedimentary rock during the complete stress-strain path[J]. Journal of China Coal Society, 2000, 25(2): 113-116.

[3]彭苏萍, 孟召平, 王虎, 等. 不同围压下砂岩孔渗规律试验研究[J]. 岩石力学与工程学报, 2003, 22(5): 742-746.PENG Su-ping, MENG Zhao-ping, WANG Hu, et al. Testing study on pore ratio and permeability of sandstone under different confining pressures[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(5): 742-746.

[4]姜振泉, 季梁军. 岩石全应力-应变过程渗透性试验研究[J].岩土工程学报, 2001, 23(2): 153-156.JIANG Zhen-quan, JI Liang-jun. The laboratory study onbehavior of permeability of rock along the complete stress-strain path[J]. Chinese Journal of Geotechnical Engineering, 2001,23(2): 153-156.

[5]姜振泉, 季梁军, 左如松, 等. 岩石在伺服条件下的渗透性与应变、应力的关联性特征[J]. 岩石力学与工程学报, 2002,21(10): 1442-1446.JIANG Zhen-quan, JI Liang-jun, ZUO Ru-song, et al.Correlation among rock permeability and strain, stress under servo-control condition[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(10): 1442-1446.

[6]朱珍德, 张爱军, 徐卫亚. 脆性岩石全应力-应变过程渗流特性试验研究[J]. 岩土力学, 2002, 23(5): 555-559.ZHU Zhen-de, ZHANG Ai-jun, XU Wei-ya. Experimental research on complete stress-strain process seepage characteristics of brittle rock[J]. Rock and Soil Mechanics, 2002, 23(5):555-559.

[7]韩宝平, 冯启言, 于礼山, 等. 全应力应变过程中碳酸盐岩渗透性研究[J]. 工程地质学报, 2000, 8(2): 127-129.HAN Bao-ping, FENG Qi-yan, YU Li-shan, et al. Study on the permeability of carbonate during full periods of stress-strain[J].Journal of Engineering Geology, 2000, 8(2): 127-129.

[8]王金安, 彭苏萍, 孟召平. 岩石三轴全应力应变过程中的渗透规律[J]. 北京科技大学学报, 2001, 23(6): 489-491.WANG Jin-an, PENG Su-ping, MENG Zhao-ping. Permeability rule in full strain-stress process of rock under triaxial Compression[J]. Journal of University of Science and Technology Beijing, 2001, 23(6): 489-491.

[9]李长洪, 张立新, 姚作强, 等. 两种岩石的不同类型渗透特性实验及其机理分析[J]. 北京科技大学学报, 2010, 32(2):158-164.LI Chang-hong, ZHANG Li-xin, YAO Zuo-qiang, et al.Permeability characteristics experiment and its mechanism analysis of two types of rocks[J]. Journal of University of Science and technology Beijing, 2010, 32(2): 158-164.

[10]杨天鸿, 唐春安, 朱万成, 等. 岩石破裂过程渗流与应力耦合分析[J]. 岩土工程学报, 2001, 23(4): 489-494.YANG Tian-hong, TANH Chun-an, ZHU Wan-cheng, et al.Coupling analysis of seepage and stresses in rock failure process[J]. Chinese Journal of Geotechnical Engineering, 2001,23(4): 489-494.

[11]杨天鸿. 岩石破裂过程渗透性质及其与应力耦合作用研究[D].沈阳: 东北大学资源与土木工程学院, 2001: 61-63.YANG Tian-hong. Study on infiltrate character and coupling analysis of seepage and stress in rock failure process[D].Shenyang: Northeastern University. School of Resource and Civil Engineering, 2001: 61-63.

[12]刘洪磊, 杨天鸿, 于庆磊, 等. 凝灰岩破坏全过程渗流演化规律的实验研究[J]. 东北大学学报: 自然科学版, 2009, 30(7):1030-1033.LIU Hong-lei, YANG Tian-hong, YU Qing-lei, et al.Experimental study on fluid permeation evolution in whole failure process of tuff[J]. Journal of Northeastern University:Natural Science, 2009, 30(7): 1030-1033.

[13]仵彦卿, 曹广祝, 王殿武. 基于X-射线CT方法的岩石小裂纹扩展过程分析[J]. 应用力学学报, 2005, 22(3): 484-492.WU Yan-qing, CAO Guang-zhu, WANG Dian-wu.Microfracturing processes of rock by real-time observation of X-ray CT[J]. China Journal of Applied Mechanics, 2005, 22(3):484-492.

[14]Bieniawski Z T. Time-dependent behaviour of fractured rock[J].Rock Mechanics and Rock Engineering, 1970, 2(3): 123-127.

[15]秦四清, 徐锡伟, 胡平, 等. 孕震断层的多锁固段脆性破裂机制与地震预测新方法的探索[J]. 地球物理学报, 2010, 53(4):1001-1014.QIN Si-qing, XU Xi-wei, HU Ping, et al. Brittle failure mechanism of multiple locked patches in a seismogenic fault system and exploration on a new way for earthquake prediction[J]. Chinese Journal of Geophysics, 2010, 53(4):1001-1014.

[16]Hudson J A, Fairhurst C. Tensile strength, Weibull’s theory and a general statistical approach to rock failure[C]//The Proceedings of the Southampton 1969 Civil Engineering Materials Conference. Southampton, England, 1969: 901-914.

[17]Allegre C J, Mouel J L L, Provost A. Scaling rules in rock fracture and possible implications for earthquake prediction[J].Nature, 1982, 297: 47-49.

[18]Smalley R F, Turcotte D L, Solla S A. A renormalization group approach to the stick slip behavior of faults[J]. J Geophys Res,1985, 90: 1894-1900.

[19]Wilson K G.. Problems in physics with many scales of length[J].Sci Am, 1979, 241: 158-179.

[20]冯增朝, 赵阳升, 吕兆兴. 强随机分布裂隙介质的二维逾渗规律研究[J]. 岩石力学与工程学报, 2006, 25(S2): 3904-3908.FENG Zeng-chao, ZHAO Yang-sheng, LU Zhao-xing. Research on laws of 2D percolation of fully random distribution fracture media[J]. Chinese Journal of Rock Mechanics and Engineering,2006, 25(Supp.2): 3904-3908.

[21]陈忠辉, 谭国焕, 杨文柱. 岩石脆性破裂的重正化研究及数值模拟[J]. 岩土工程学报, 2002, 24(2): 183-187.CHEN Zhong-hui, TAN Guo-huan, YANG Wen-zhu.Renormalization study and numerical simulation on brittle failure of rocks[J]. Chinese Journal of Geotechnical Engineering,2002, 24(2): 183-187.

[22]曹文贵, 赵明华, 刘成学. 基于 weibull分布的岩石损伤软化模型及其修正方法研究[J]. 岩石力学与工程学报, 2004,23(19): 3226-3231.CAO Wen-gui, ZHAO Ming-hua, LIU Cheng-xue. Study on model and its modifying method for rock softening and damage based on weibull random distribution[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3226-3231.