民用飞机供应商评估体系研究
2012-07-31徐建新郭巧荣
徐建新,李 洋,郭巧荣
(中国民航大学航空工程学院,天津 300300)
国家将大型飞机的研制作为重大科技专项,明确提出大型飞机项目采用“主制造商——供应商”模式,因此,对供应商评估问题的研究,将不仅有利于大型飞机项目的顺利进行,同时也将进一步推动国内民用航空产品研制体系的改善,从而为今后民用飞机的全面自主发展打下坚实的基础[1]。
本文针对民用航空制造业的特点,制定了不同类型民用飞机供应商的评估指标体系,利用层次分析法对民用飞机供应商进行评估。
1 层次分析法的基本原理
对于n阶矩阵A,如果存在常数λ和非零n维向量x,使得Ax=λx成立,则称λ是矩阵A的特征值,非零向量x是矩阵A关于λ的特征向量。
设n个物体体积分别为v1、v2、…、vn。不知道物体的体积大小,只知道两两之间的比值aij=vi/vj,已知aij(1≤i,j≤n),令

显然 aij满足:① aij>0;② aij=1/aji。称满足①、②的矩阵A为正互反矩阵。若③aijajk=aik(1≤k≤n),则称满足①、②、③的矩阵A为一致性判断矩阵。
令 v=(v1,v2,…,vn)T,则 Av=nv,即 n 是矩阵 A的特征值,v是矩阵A的属于特征值n的一个特征向量。
易知,n是一致性判断矩阵A的最大特征值,v是一致性判断矩阵A的属于最大特征值的一个特征向量,v的n个分量是物体的体积大小。由此,可以用特征向量表示物体的体积大小排序[2]。
如果aij不再是真实的体积比值,显然矩阵A会不满足一致性条件,此时A的最大特征值λmax不再是n,λmax对应的特征向量也不会是n个物体的真实体积大小。
但如果体积比aij的变化不大,最大特征值λmax与n相差很小,即矩阵一致性程度较好,则可以采用矩阵最大特征值对应的特征向量归一化,来反映物体的体积大小排序。对于如何衡量aij的变化,可采用一致性指标 CI,令
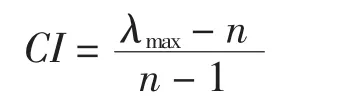
其中:λmax为矩阵最大特征值;n为矩阵阶数。
一致性指标CI的值越小越好,为了衡量一致性指标的大小,引入平均随机一致性指标RI。平均随机一致性指标是指多次重复进行随机判断矩阵最大特征值计算之后取算数平均值得到的。龚木森、许树柏[3]得出的1~6阶重复1 000次的平均随机一致性指标如表1所示。

表1 平均随机一致性指标Tab.1 Average random consistency index
令一致性比率CR为

当CR<0.1时认为判断矩阵的一致性是可以接受的,即认为此时最大特征值λmax对应的特征向量归一化后,能给出 n个物体 v1、v2、…、vn按体积大小的排序。
综上可以看出,层次分析法理论并不严谨,但仍是一种能有效处理排序问题的实用方法,由此得到层次分析法基本步骤如下:
首先,把复杂问题分解为称之为元素的各组成部分,把这些元素按属性不同分成若干组,以形成从上层到下层有支配关系的递阶层次。最上层一般是问题的预定目标;中间层为实现目标所涉及的中间环节;最下层包括了为实现目标可供选择的方案等。
然后,构造判断矩阵。判断矩阵表示针对上一层次,本层次元素之间两两比较的相对重要性,这个相对重要性用数值表示就构成判断矩阵。通常采用1~9标度法[4],它是一种将思维判断数量化的方法。在区分物质差别时,人们通常用相同、略、较、很、绝对的语言,进一步细分,可以在相邻两级中插入折中想法。
层次分析法的关键步骤是构造判断矩阵,判断矩阵的一致性程度直接影响到方案评估的有效性。导致矩阵不一致性的主要原因是判断矩阵的构造过程中没有保持一致的逻辑思维。例如,A比B重要,B比C重要,C比A重要,显然逻辑上错误。为避免逻辑思维的错误,可采用如下方法。
对于表2的判断矩阵,Xi(Xj)的取值为1~9,两两比较,当取值Xi>Xj时,由式(1)进行计算,当取值Xi<Xj时,由式(2)进行计算。由此构造判断矩阵,相对简单且能保证构造过程逻辑思维的一致。
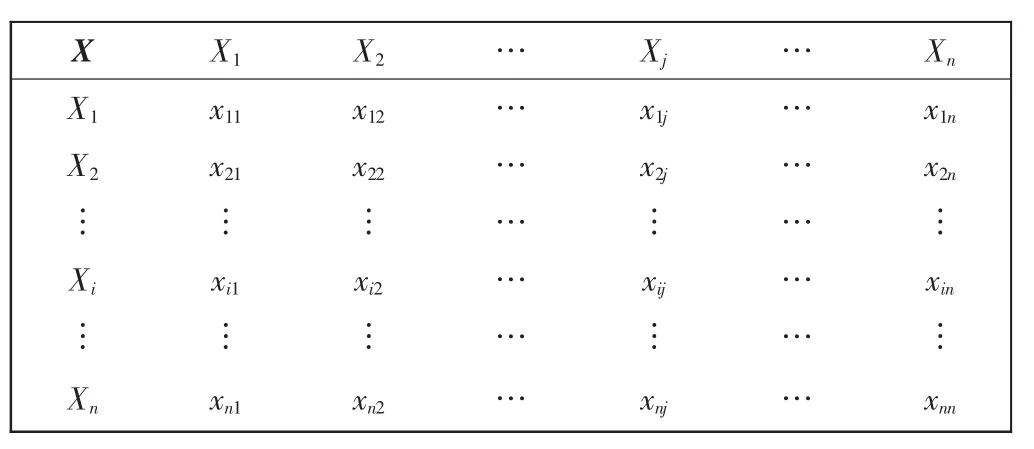
表2 判断矩阵Tab.2 Judgment matrix

最后,计算层次单排序和组合权重。层次单排序就是根据判断矩阵,计算对于上一层某元素而言,本层次与之有联系的元素重要性程度的相对值。同一层次所有元素对于总目标相对重要性的排序权值称为组合权重,此过程是从顶层到底层逐层进行的,对于顶层下面的第2层,其层次单排序即为总排序。
层次分析法将问题按照分解、比较、综合的思维方式进行研究,将定性问题定量化,适用于多准则的决策系统评估[5-7]。
2 民用飞机供应商评估体系设计
2.1 供应商分类及评估指标设计
为实现对不同类型民用飞机供应商的有效评估,根据民用航空产品和零部件特点,结合国内航空制造业的现状,可将供应商分为3类:①一般供应商:制造一些基本机体部件或提供原材料的供应商;②重要供应商:生产一些重要部件或系统的供应商;③核心供应商:具有垄断技术,制造关键部件和系统的供应商,如发动机制造商。
对民用飞机供应商进行评估可以从质量、价格、交付、服务、管理5方面准则考虑。但由于供应商的类型不同,对各准则的参考侧重有所不同[8-9]。
对于质量准则,相比一般供应商,核心供应商和重要供应商都具有良好的质量保障体系,差别性较小,故评估时不予参考。
针对核心供应商,可从质量、价格和服务3个准则考虑。其中,质量准则里需要格外考虑其技术创新能力;因其产品价格普遍较高,故要考虑支付周期;考虑到其在技术方面的垄断优势,很难开展技术合作,因此更多考虑技术与备件支持。
管理水平是影响企业资源有效利用率的重要因素。对于重要供应商,将其管理能力描述为生产管理和人力资源管理,便于进行量化比较;而一般供应商,还需要关注适航管理能力,即以保障民用航空器安全性为目标的技术管理能力[10]。
由此制定评估3类供应商的主要准则和指标,如表3所示。
2.2 供应商的评估过程
以一般供应商的评估为例,计算准则与指标的权重,并选取3家供应商进行评估。
2.2.1 建立多层次评估结构模型
构建4层模型(如图1所示):第1层为目标层A,即一般供应商的评估;第2层为准则层B,包含有质量、价格、交付、管理4个准则;第3层为指标层C,主要为具体的指标;第4层为方案层D,即备选的供应商。
2.2.2 构造判断矩阵
以构造准则层B对目标层A的判断矩阵为例。对一般供应商的准则层评分,如表4所示,通过式(1)、式(2)构造判断矩阵,结果计入表5。

表3 供应商评估准则和指标Tab.3 Supplier evaluation criteria and indicators

表4 一般供应商准则层评分表Tab.4 Criteria of general supplier score sheet
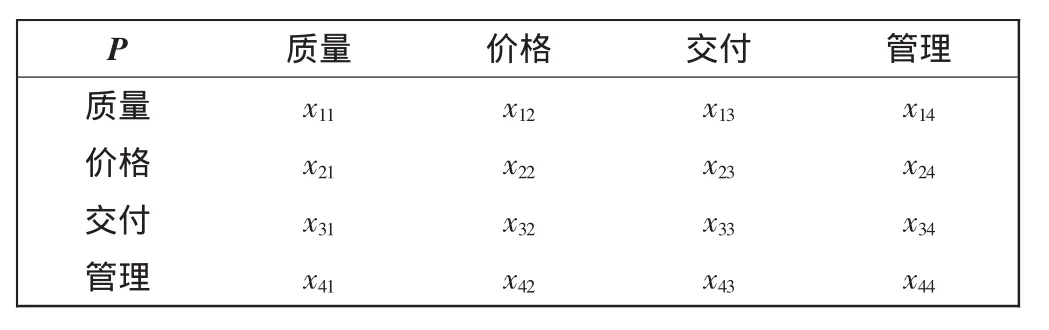
表5 判断矩阵表Tab.5 Judgment matrix sheet
由此可得准则层B对目标层A的判断矩阵P为


2.2.3 指标权重计算及一致性检验
对于判断矩阵P,最大特征值λmax=4.144,一致性比率CR=0.054<0.1,满足一致性要求。
因此,将其最大特征值对应的特征向量归一化,即为准则层B对目标层A的权重向量w(B-A)。
同理,依次计算出指标层C对准则层B的权重向量w(C-B)。
由此可得一般供应商的评估准则指标权重,如表6所示。

表6 一般供应商评估准则指标权重Tab.6 Relative weight of general supplier evaluation
2.2.4 方案评估
对于供应商甲、乙、丙,依次对11项指标评分,构造判断矩阵,计算权重向量。
例如,对于指标“紧急备件”能力,对供应商甲、乙、丙打分如表7所示,通过式(1)、式(2)构造判断矩阵,计算权重向量。

表7 供应商评分表Tab.7 Supplier score sheet
同理,可得供应商甲、乙、丙相对于每一个指标的权重向量 w(D-C1)、w(D-C2)、…、w(D-C11)。构成向量组w(D-C)=(w(D-C1),w(D-C2),… ,w(D-C11))。
由此,方案层D对目标层A的组合权重w(D-A)=w(D-C)w(C-A)=(0.415,0.298,0.285),即可得出,供应商甲为相对最优的供应商。
3 评估系统的建立与实现
3.1 评估系统简介
层次分析法方法简洁,用法灵活,但涉及大量矩阵运算,计算较为繁琐。本文基于MATLAB GUI(graphical user interfaces,图形用户界面)编程设计[11],不仅使层次分析法计算变得相对较简单,而且为决策者提供了友好的人机交互界面,如图2所示。

3.2 系统运行流程
首先,确定需要的产品,即确定评估的目标层。根据产品,得出备选供应商,即确定方案层。然后,选定供应商类型,得出准则和指标。最后,通过层次分析法计算得出评估结果。
3.3 实例
假设需确定某机体部件的供应商,有供应商甲、乙、丙3家供应商备选,此类供应商为一般供应商,因此侧重考虑的一级准则有质量、价格、交付、管理。
依次对每个供应商的各一级准则下的二级指标评分,构造对应的判断矩阵,计算一致性比率,完成3家供应商在单项指标下的排序,如图3所示。

完成各项指标的权重向量计算,最后计算组合权向量,即可得出评估结果。
5 结语
本文根据民用航空制造业的特点,建立了不同类型民用飞机供应商的评估指标,利用层次分析法对供应商进行评估。
而要完善民用飞机供应商的评估体系是一个长期的过程,需要主制造商和供应商的共同努力。后期随着数据的不断积累及使用者的反馈,不断修正评估体系中的指标及其权重,为民用飞机供应商的评估提供更好的决策支持。
[1]黄 强.中国民机产业崛起之探索[M].北京:航空工业出版社,2007.
[2]程乾生.层次分析法AHP和属性层次模型AHM[J].系统工程理论与实践,1997(11):25-28.
[3]许树柏.层次分析法原理[M].天津:天津大学出版社,1988.
[4]胡明甫.AHP层次分析法及MATLAB的应用[J].钢铁技术,2004(2):43-46.
[5]CHARLES A WEBER,JOHN R CURRENT,BENTON W C.Vendor selection criteria and methods[J].European Journal of Operational Research,1991,50(1):2-18.
[6]PATTON W E.Use of human judgment models in industrial buyers′vendor selection decisions[J].Industrial Marketing Management,1996,25(2):135-149.
[7]MAGGIE C Y,TAM V M,RAO TUMMALA.An application of the AHP in vendor selection of a telecommunications system[J].International Journal of Management Science,2001,29(2):171-182.
[8]周 媛,左洪福.民机供应商综合评估实证研究[J].科技管理研究,2010(18):70-72.
[9]王 园.航空制造业供应商评估体系研究[D].西安:西安电子科技大学,2010.
[10]中国民用航空局航空器适航司.中国民用航空器适航管理[M].北京:中国民航出版社,1994.
[11]罗华飞.MATLAB GUI设计学习手记[M].北京:北京航空航天大学出版社,2009.
