提琴琴头侧面螺旋线的绘制
2012-07-31陈婷
陈 婷
(中央音乐学院 提琴制作教研室, 北京 100031)

1 绪论
提琴琴头可分为三个面:正面、背面和侧面,其中侧面曲线是人们研究最多、也最能反映制作者个性的曲线。提琴制作已经有几百年的历史,其间曾经有许多人尝试着改变提琴琴头曲线的设计,有人头形状、兽头形状等,但都未广泛传播,至今应用最多的仍是螺旋型曲线。螺旋型曲线本身给人以一种动态的美感,不同的提琴制作者采用的曲线都有各自的特点。几位著名的提琴制作大师的琴头曲线一直都是后世的提琴制作者们研究的重点。
琴头侧面曲线又分为琴头螺旋展开线和琴头身曲线,下面要讨论的是琴头侧面曲线的上半部分螺旋展开线的画法,即从琴头眼珠到琴头侧面后背最宽处。本文浅要地分析和比较尼古拉·阿玛蒂(Niccolò Amati 或Nicolo Amati)、安东尼奥·斯特拉地瓦里(Antonio Stradivari)和约瑟夫·瓜纳里(“耶稣”·瓜纳里)(Giuseppe Guarneri del Gesù) 琴头侧面螺旋线的设计思路,进行提琴琴头设计探索性的尝试。
2 琴头侧面螺旋线的画法
2.1 黄金分割的应用
在古希腊时期,黄金分割及其几何比例(黄金分割率)已经大量运用于各领域,乐器制作也不例外。黄金分割之所以能够在建筑、美术、雕刻、音乐等方面广泛应用,是因为它可以用简单的尺规工具找出,并且符合人们的审美标准。
黄金分割的几何意义可以简单地表达为:整条线段的长与所分成的两条线段之中较长一段线段的比值,同较长线段与较短线段长度的比值相等。这个比值叫做黄金分割比,也叫黄金分割率,用Φ表示, Φ≈1.618。
黄金分割在提琴琴头中的应用相对较少,也相对比较独立,在《提琴与黄金分割率》一书中曾经运用黄金分割率对斯特拉地瓦里的琴头作了一些分析,在等角螺线的绘制中也有应用。在本文中笔者也将部分运用黄金分割率画出琴头侧面螺旋展开线。
2.2 等角螺线画法
2.2.1 等角螺线的定义
等角螺线是螺旋形的,也称为对数螺线(柏努利曲线),其数学公式是:r=kecα。等角螺线的代数表达式早在1640 年就发现了。笛卡尔(Descartes )和柏努利(Bemoulli)在1691~1693 年开始研究等角螺线,他们是首先研究等角螺线的数学家。等角螺线被广泛用于建筑装饰。
等角螺线的显著性质包括(见图1 ):
(1)等角螺线按几何比率增长,因此,任意的半径被螺线所截的线段构成等比级数,也就是说,半径被相邻螺线所截线段呈等比,如OA/OG。
(2)直径的两个端点到极点的距离呈等比,如:OA/OC。相互垂直的半径呈等比,如:OA/OB。
(3)等角螺线的特征角a,也就是半径与螺线切线的夹角是常数(另外,当等角螺线旋转时,它的大小变了,但它的形状却保持不变)。
所有曾经深入研究过等角螺线的学者们都发现,在自然界中有三种“主要螺线”。这三种主要等角螺线的半径增量分别等于Φ、Φ2或Φ4。这三种螺线也是提琴制圈中最经常使用到的,在此我们将进行具体的讲解。
2.2.2 三种重要的等角螺线及其画法
⑴ 半径增量=φ 的等角螺线 (见图1)
最简单的等角螺线是由一个等比数列所定义的:如果以点O为极点,等角螺线分任意半径OA 所得线段OL、OG、OA……的长组成等比数列:
OG/OL=OA/OG= …… =Φ
且AC为直径, BE⊥AC,则:
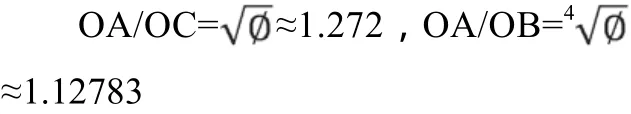
特征角≈85°36′。
这一等角螺线非常“和谐”并符合美学原理。
Grosjean J.P.给出了这个等角螺线一个尺规作图法(图1 ):
首先作矩形ABCD,使得其两边之比:
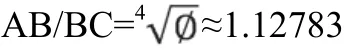
如果AB=5 cm,那么,最终画出的等角螺线就是小提琴琴头的外轮廓尺寸。
连接对角线AC,过点B作AC的垂线并延长,垂点为点0,交CD于点F,交AD延长线于点E。
依次作直线FG、G H、H J、JK……,分别平行于直线AE、AB、BC、CF……,且与直线AC、BE依次交于点G、H、J、K……。另外,从线段CF能计算线段FG的长度,因为CF/FG =l.l2783 。由此我们获得一个等角螺线的规则区间。
然后进行如下步骤:
过线段AE的中点I 作线段AE的中垂线IR。

以点I为圆心,IA为半径画弧交IR于点R。
以点R为圆心,RA为半径画弧AE,则弧AE即为等角螺线的一部分。
对于线段AB、BC、CF、FG等重复上述步骤,即可获得一条近似的等角螺线。
⑵ 半径增量=φ2的等角螺线(见图2)
在这一等角螺线上,半径增量为Φ2,也就是说任意半径被螺线分割的两个相邻截点到螺线极点的距离之比等于Φ2,即:
OA/OE=Φ2,则有
应用这些数据,按照前述的方法,同样可以构造一个矩形来给制这一等角螺线,其特征角≈81°22′。
⑶ 半径增量=φ4的等角螺线
这一等角螺线的半径增量为Φ4(≈6.854)。可先绘制矩形Φ,这一等角螺线相互垂直的半径之比Φ。它的特征角≈73°43′。
矩形Φ:设矩形的长度为L,宽度为1,则L/I=Φ。在矩形Φ内,通过将矩形的长或宽按黄金分割比进行反复分剖,可以得到一系列长宽比等于Φ的矩形。而我们获得的这些矩形的边长也组成了一个公比为Φ 的等比数列。通过这些矩形,分别以每个矩形的宽为半径画1/4 圆弧,就可以连成一条半径增量为Φ4的等角曲线。
矩形Φ反复分割所得的图形具有典型的数学特征,这是磐折形(gnomonic)的一种。磐折形,按照亚里斯多德(Aristotle) 的定义,是“某个平行四边形在其一角切除一个较小的相似四边形后的剩余部分”。
在矩形ABEF中, EB/BA=Φ(图3 ),这个矩形的磐折形ABCD 是个正方形。依次进行分割所得到的磐折形也都是正方形,这样,我们得到了一组看起来象是绕着等角螺线极点旋转的正方形。
由此,我们通过一些简单的辅助,找到了一个绘制等角螺线近似曲线的简易方法。自然界中随处可观察到等角螺线,如加莱克斯草、螺类的外壳、一些植物及DNA 链。它在建筑业上也有广泛的应用,因为它给人一种动态的和谐美感。
从对现实的观察开始,一些现代科学家进一步发现斐波纳契(Fibonacci) 数列的各项趋向于黄金分割,并且这也是组成生命的基础:“自然界中存在这些数字,这些数字也是组成DNA 的四种碱基T 、C、A 和G的比例,所有的生物,无论是人、蔬菜还是动物,其遗传信息都是依靠这四种碱基的不同组合来表达:所有宏观的表现型都在DNA上有其相应的基因型”。用现代的语言来说,根据古人的世界观,所有的事都是定数,而这个数就是黄金分割数。
等角螺线的属性非常特别,以至于数学家柏努利要求将之刻在自己的墓碑上,并附词“纵使改变,依然故我”(Eadem Mutata Resurgo)。
将等角螺线作某些变换时,所得的曲线仍是全等的等角螺线。这些变换包括:求等角螺线的垂足曲线(pedal curve)、渐屈线(evolute)、反演曲线(inversive curve)、焦线(caustic curve) 以及将等角螺线以其极点为中心作伸缩变换(dilation)。由于这些变换都可以使等角螺线再生,所以,斯特拉地瓦里使用等角螺线而不使用阿基米德(A rchimedes)螺线来画小提琴的旋首曲线,因为阿基米德螺线是“纯粹的静态曲线,表现出一种一成不变的律动,这点与等角螺线和其他指数曲线相反”。正是因为其缺乏“动态感”,所以斯特拉地瓦里更喜欢用等角螺线绘制小提琴曲线。

因此,从那时起,等角螺线常规用于提琴家族的制图也就不足为怪了。
2.3 尺规作图法
在300多年前,由于科学的发展还处于初级阶段,绘图工具仅限于直尺、圆规等简陋工具,那么提琴制作大师们如何绘制精美的乐器图的呢?下面介绍几种简单的尺规作图法。
2.3.1 二心法(半圆法)
作一水平直线,在其上取两点A和B ,相距约6 mm ,先以A为圆心AB为半径r作半圆,然后再以B为圆心,以2r为半径接前半圆再画半圆,就这样A、B交替为圆心,以r、2r、3r……作半径,画出的螺线路2~3 圈即为琴头曲线(图4)。
2.3.2 三心法(1/3 圆法)
作一边长约6 mm 的等边三角形,依次以三个顶点为圆心,第一次以边长为半径r作1/3圆周,然后换个顶点为圆心,半径增加一个边长再作1/3圆周,依此类推,画出2~3圈螺旋线,即得琴头曲线(图5)。
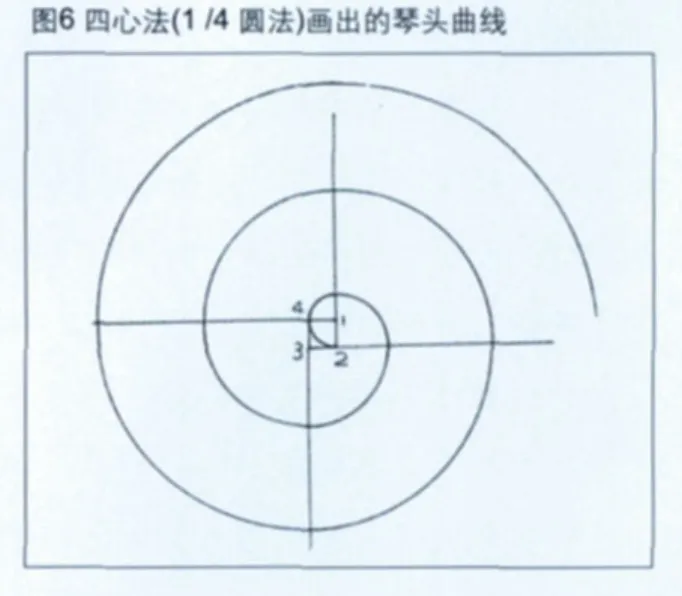
2.3.3 四心法(1/4 圆法)
作边长约6mm 的正方形,依次以四个顶点为圆心,第一次以边长为半径r作1/4 圆周,以下的画法与三心法类似(图6)。
在阿玛蒂、斯特拉地瓦里、瓜纳里的琴头中,我们发现其螺旋展开线并不能完全用等角螺线或简单的尺规作图法来绘制,他们之间虽有相似性,却又各自有各自的特点。因此,在他们的作品中各自选出一个具有代表性的琴头作分析。


3 阿玛蒂、斯特拉地瓦里、瓜纳里琴头侧面螺旋线的设计
3.1 阿玛蒂琴头侧面螺旋线的设计
尼古拉·阿玛蒂崇尚完美与和谐,他的作品做工精湛,处处体现了和谐美,圆与流畅是他要表现的主题。
他的1675 年琴头螺旋展开线的特点是:线条圆润、均匀,很接近等角螺线。如果在眼珠中心位置画一水平线,以眼珠中心为轴,将此直线向琴头前下方旋转30°角,则眼珠结束位置在这条线上(图7)。

3.2 安东尼奥·斯特拉地瓦里琴头侧面螺旋线的设计
作为尼古拉· 阿玛蒂的学生,在安东尼奥·斯特拉地瓦里早期作品中,与阿玛蒂的作品有很多相似之处,在脱离了阿玛蒂之后,随着对琴型设计的改进,他逐渐形成了自己的风格,并于1700年左右进入了事业的黄金时期。他的1699 年琴头螺旋展开线的特点是:与尼古拉·阿玛蒂相比,他的琴头眼珠结束位置也是在旋转30°角的直线上,并以此直线为长轴,有椭圆形拉长趋势。这样使他的琴头曲线产生了变化,不再是均匀稳定的,而产生了一定的节奏,张弛有度地动感使琴头有一定的冲突,更具魅力(图8) 。


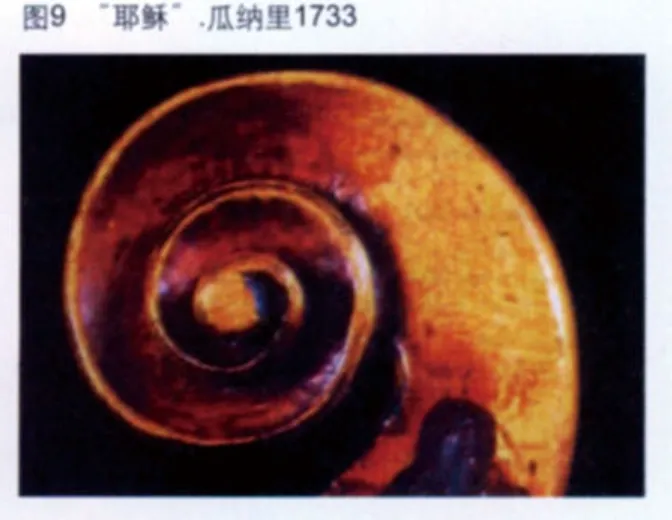
3.3 “耶稣”·瓜纳里琴头侧面螺旋线的设计
“耶稣”·瓜纳里的爷爷也是尼古拉·阿玛蒂的学生,他是一个非常有个性的人,工作起来很自由无拘束,他并不努力以细致精确的传统风格来雕刻木材,人们仔细观察他制作的琴头时,特征就很清楚,上面的凿痕清晰可见。
他的琴通常分为四个不同的类型,每个阶段都有各自的特征。有迹象表明,“耶稣”的制作方法是在不断变化和发展。
第一阶段,从1726年至1730年,明显表示他是一位训练有素的艺人,这大概是人们对他从父亲那里所受教育的赞扬,他的琴在风格上与其父亲有相似之处。
第二阶段,从1730 年至1735 年,以成熟并更具独到见解的制作方法为特征:琴身各段伸长,f孔比较细长,琴边、琴角和琴头的最后润饰相当完美。从各个角度看,琴头旋首两边相互十分对称,有个事实值得考虑,分开观察,两面的外形显得那么不同。
第三阶段,从1735年至1740年,风格表现得越来越自由,甚至制作方法也失去了控制。他的琴头有时只是对前辈的端庄构思的夸张性仿造,但更显个性。
最后一个阶段,从1740 年至1744 年,“耶稣”的作品过于违反公认的制作规范,从某种程度讲, 一些评论家厌恶这种草率行事的现象。
在“耶稣”·瓜纳里的作品中,经常有即时性和独创性的成分,而且决不迂腐。
他的1733 年琴头螺旋展开线的特点是:线条走向不均匀,有冲突。在旋转30°角的直线轴方向有椭圆形拉长趋势,这点与斯特拉地瓦里的琴头相似。在最后一圈眼珠处向下压,使里圈长轴方向显得更拉长,眼珠结束处向上提升,甚至超过45°角。在琴头前下方处略宽。琴头顶部略靠前处稍高,转到后背处略收紧。
(本文节选自陈婷硕士毕业论文《提琴琴头侧面螺旋线的绘制》)
[1]Eric L.Brooks,Jean-André Degrotte: THE VIOLIN AND THE GOLDEN NUMBER,2005.P53
[2]Grosjean J.P.: LE NOM BTRE D' OR 1.618.MODE D' EMPLOI EN DESICN ET ESTHÉTIQUE INDUSTRIELLE,2e Ed.Ed.H.Vial,1993.P144-145
[3]M atila C.Gh y ka: ESTHÉT IQUE DES PROPORTIONS DANS LA NATURE ET DANS LES ARTS,Ed.Gallimard ,Paris,1927/Ed.du Rocher,1987.P146一147
[4]龙树德编:《制图基础和提琴制图》,1999.P127-128
[5](英) 克里斯·约翰逊,罗伊·考特诺尔著《小提琴制作艺术》,2003.P24-25
