基于相移偏移和匹配追踪的探地雷达成像方法

张建中 黄月琴

（1.中国海洋大学海洋地球科学学院，山东 青岛266100；2.厦门大学物理与机电工程学院，福建 厦门361005）

引 言

偏移成像是探地雷达（GPR）目标识别和定位的主要技术之一。相移偏移方法因简单实用被广泛用于GPR成像［1－4］，这类方法中的一个重要步骤是用反傅里叶变换把波数域的相移数据变回到空间域。但是，由于均匀采样频率与波数之间的非线性关系，使得波数空间的波场被非均匀采样，常规的快速傅里叶变换（FFT）难以直接使用。现有的做法是先对波数空间非均匀采样的波场进行插值运算，获得均匀采样的波数空间波场，再直接使用FFT，如线性插值－FFT 算法［5］，Stolt插 值－FFT 算 法［6－7］等。虽然FFT运行很快，但插值的计算量却较大，而且，插值后的波场将不可避免地含有一定的误差，从而影响成像精度。Liu等人［8］提出了精确的非均匀采样快速傅里叶变换算法（NUFFT）。把NUFFT引入到相移算法中，可以避免插值运算，使成像精度和计算效率得到进一步的提高。

实测GPR数据通常被噪声所污染，致使偏移成像质量和目标定位精度受到严重影响。匹配追踪（MP）算法［9］是目前最流行的信号分析工具之一，被用于地震和雷达信号处理中［10－12］。MP算法选择一个超完备展开函数集合，根据信号特征，自适应地选择展开函数，通过逐步逼近，求得信号的表示，达到分解信号和去除噪声的效果。但是，MP算法在每一次求解的分解过程中，需要在超完备展开函数集合或原子库中寻找最优原子，这是一个非常耗时的过程，导致MP算法具有很大的计算量，从而限制了该算法的实际应用。为此，将最小二乘原理引入到MP算法中，直接计算最优原子参数，避免了在庞大的原子库中搜寻最优原子的耗时过程，形成了具有较高计算速度的最小二乘匹配追踪算法（LSMP）。

根据相移偏移方法和MP算法的上述问题和改进途径，对它们进行了改进，并把它们综合起来，对GPR资料进行成像处理，获得了偏移结果的振幅谱和相位谱，显示出了良好的成像效果。

1 改进的相移偏移方法

相移偏移算法属于频率－波数域方法，是目前常用的GPR偏移成像方法之一。该方法所要解决的问题可描述为：利用地表z＝0处接收的GPR信号s（x，z＝0，t）来重建波场s（x，z，t＝0）.其方法原理如下：

1）对GPR回波信号s（x，z＝0，t）进行二维傅里叶变换，得

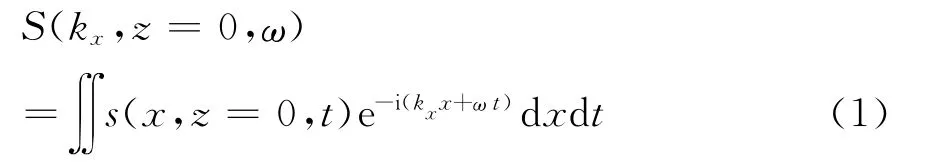
2）在频域－波数空间，任意深度z处的波场S（kx，z，ω）可由z＝0处的波场表示为

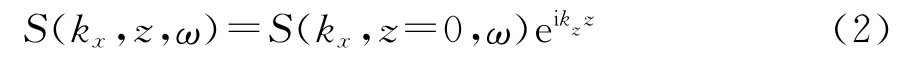
式中kz是z方向波数。kx，kz和ω满足

式中ν是电磁波在地下的平均传播速度。

3）对式（2）进行二维反傅里叶变换，可得时域空间内任意深度z处的波场为

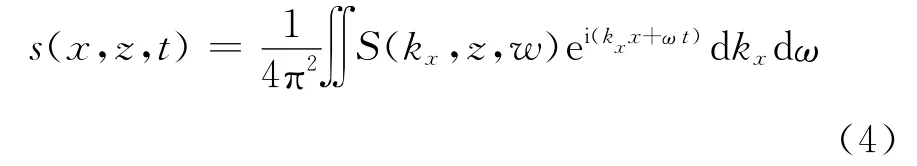
4）将式（2）代入在式（4），并令t＝0，就得到偏移后的波场s（x，z，t＝0）为

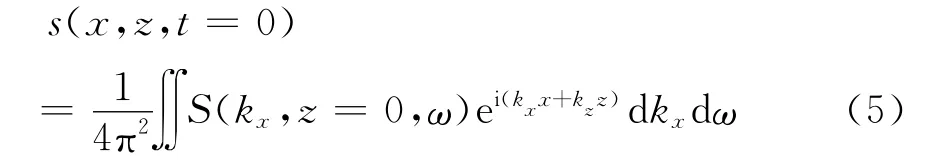
由于GPR系统通常在时间t方向和测线x方向上等间距采样，式（1）中傅里叶变换后的频率ω和kx波数都为均匀分布，由式（3）的非线性关系式得到的波数kz则是非均匀分布的。这样，式（5）右端实际上是一个非均匀采样的傅里叶逆变换式。为了避免因使用FFT而需要把波数空间非均匀采样数据插值成均匀采样的问题，我们采用Liu等人提出的NUFFT［8］进行快速计算。式（5）的离散形式为［13］

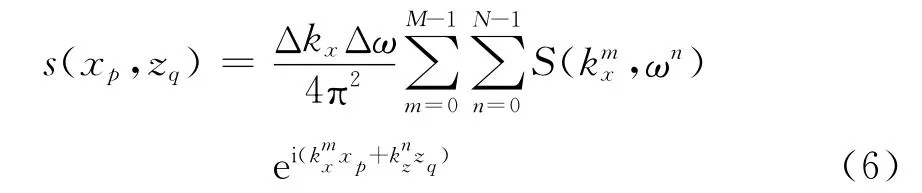
式中：Δkx和Δω为频域－波数域的采样率；M和N分别是x和t方向上的样点数；xp和zq是样点坐标。令

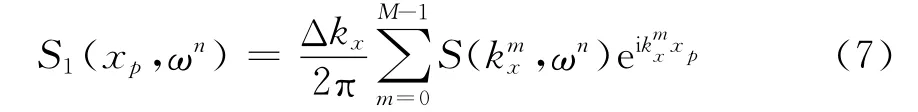
则有

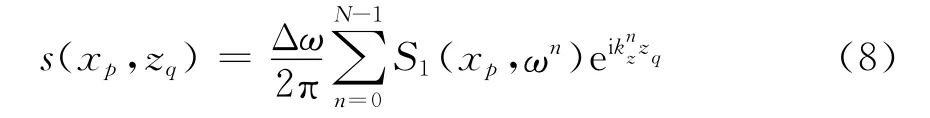
2 最小二乘匹配追踪算法

假定GPR某道回波信号u（t）可以表示成子波w（t）经过不同的时移和尺度变换后的子波的线性组合，

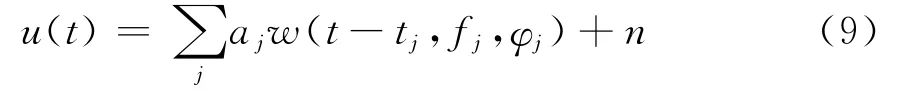
式中：aj、tj、fj和φj分别表示第j个子波的振幅、中心时间、主频和相位，j＝1，2，…，N；n是噪声。由于Ricker子波可以很好地表征GPR脉冲信号，采用Ricker子波，其表达式为

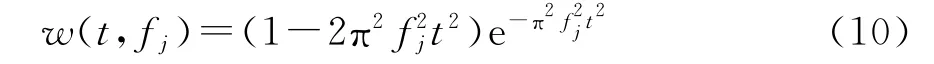
为了能够得到回波信号的振幅谱和相位谱，采用解析信号进行处理。利用Hilbert变换，GPR信号u（t）和小波w（t）的解析信号分别为

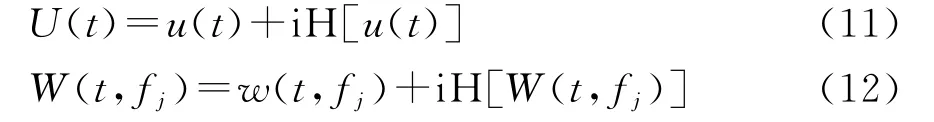
式中H表示Hilbert变换。这样，式（9）的GPR回波解析道信号可表示为

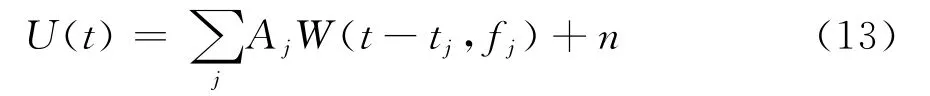
式中Aj为复振幅，且

每一次匹配追踪后的解析道信号残差R（t）为［14］

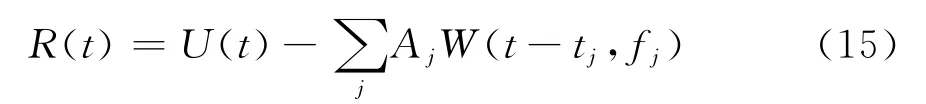
根据最小二乘原理，解析道信号残差能量定义为

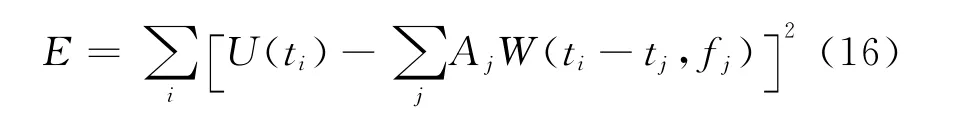
式中，ti为回波信号的时间样点，i＝1，2，… ，M.为使残差能量E达到最小，解式（16）极小值问题得到

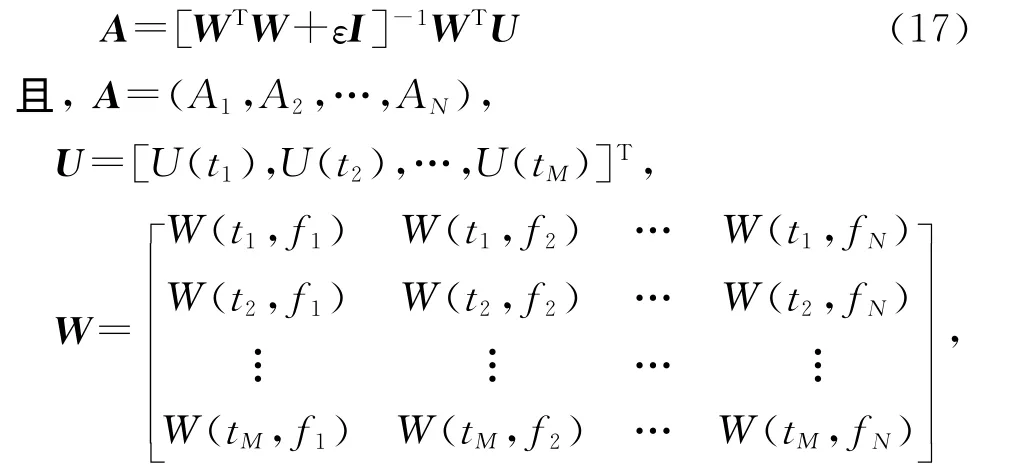
I是单位矩阵，ε是阻尼因子，T表示矩阵转置。

利用式（17）就可求出每一道回波信号的解析子波复振幅。具体计算步骤如下：

1）计算中心时间tj，即输入信号U（t）振幅包络的峰值所对应的时间。

2）计算主频fj.采取窗函数截取中心时间tj的局部波形，并利用FFT计算瞬时频谱。该频谱振幅包络的峰值所对应的频率即为所需要的主频。

3）将中心时间tj和主频fj代入式（10），并利用式（12）计算当前解析子波。

4）利用式（17）计算出复数振幅Aj.

5）由式（15）计算信号残差R（t），且令

U（t）＝R（t）.

6）计算残差能量E，并判断是否满足终止条件，若是，结束；否则，转至步骤1）。

执行上述方法步骤，就得到了组成GPR某一道随时间变化信号的各个子波的复振幅Aj.这些子波的线性叠加就近似为有效信号，而残差则被认为是噪声。去噪后的解析道信号用获得的解析子波表示为

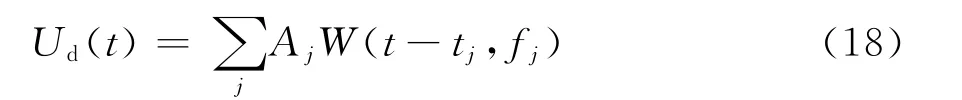
该信号的幅度谱和相位谱可分别表示为

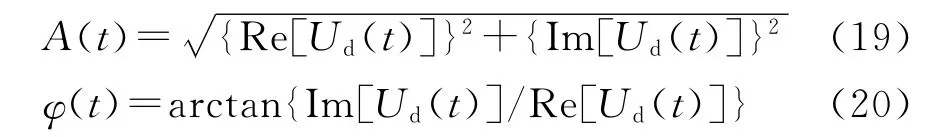
式中Re和Im分别表示取复函数的实部和虚部。

3 实验结果

分别使用数值模拟获得的GPR信号及实测的GPR资料进行实验，主要测试本文算法的去噪和聚焦性能。为了将相移偏移结果与本文的相移偏移和LSMP综合算法结果进行一一对应的比较，对相移偏移结果也通过Hilbert变换形成对应的解析信号后，再利用与式（19）和（20）类似的方法计算出相应的振幅谱和相位谱。

3.1 合成数据实验

图1（a）所示为一GPR理论模型，长度为1.4m，厚度为0.6m.背景媒质为干燥土壤，深度从0.05m到0.60m，介电常数εr为10；土壤上层为空气；土壤中分布有一个混凝土板，该板在中间部位垂直断裂而错位，板的总长度为1.4m，厚度为0.1m，介电常数εr为6.利用软件 Gpr MaxV2.0［15］模拟了该模型的 GPR记录，其中，雷达脉冲主频为900MHz.图1（b）是消除了直达波和地面反射波的模拟记录，在界面突变处有明显的绕射波，可以用来检验偏移方法的归位效果。图1（c）和（d）是在图1（b）模拟记录中加入随机噪声后的含噪记录，其中图1（c）的信噪比SNR为0dB，回波信号还比较明显，以下称为含弱噪声信号；图1（d）的信噪比SNR降为－10dB，回波信号已完全淹没在随机噪声中，以下称为含强噪声信号。为了与模型进行对比，所有图中的时间坐标被换算成了深度坐标。

分别使用改进的相移偏移方法及改进的相移偏移与LSMP综合方法对合成的无噪信号和含噪声信号进行了成像处理。图2（a）和（b）是无噪信号偏移结果的幅度谱和相位谱，断裂处的绕射波被较好的归位，说明了使用NUFFT相移偏移方法的良好效果。图2（c）和（d）是对信噪比SNR为0dB的含弱噪声信号，用相移偏移方法的幅度谱和相位谱，而图2（e）和（f）是对该含弱噪声信号用相移偏移与LSMP综合方法得到的幅度谱和相位谱。可以看出，只用相移偏移方法的结果虽然尚能反映目标，但背景噪声较大；而相移偏移与LSMP综合方法能很好的压制噪声，成像效果得到了明显改善。图2（g）和（h）是对信噪比SNR为－10dB的含强噪声信号，用相移偏移方法得到的幅度谱和相位谱，而图2（i）和（j）是对该含强噪声信号用相移偏移与LSMP综合方法得到的幅度谱和相位谱。由于目标信号几乎被强噪声淹没，在相移偏移图上噪声依然很强，而目标信号非常微弱，几乎不能识别出来；而在相移偏移与LSMP综合成像图上，噪声得到压制，目标信号反映清晰。可见，相移偏移与LSMP综合方法明显优于相移偏移方法，不仅能够对同相轴正确归位，更具有很强的压制噪声的能力，从而极大地提高了低信噪比资料的成像质量，较好地刻画目标体的位置和形状。另外，除了振幅谱外，相位谱也能较好地反映目标信息。由于相位谱反映信号相位变化的连续性，与反射信号能量无关，对于同相轴的连续展布以及突变，相位谱的特征更明显。特别是对于含噪声资料，相位谱比振幅谱能更明显地突出目标信号，因此，将幅度谱和相位谱进行综合分析，可以更好地识别和圈定目标。

3.2 实测数据实验

图3（a）是我们用pulseEKKO PRO型探地雷达在英国东约克郡的Beverley高尔夫球场采集到的雷达数据剖面图。该雷达系统采用Ricker脉冲，工作频率为500MHz，脉冲电压为180 V.共采集540道数据，道间距为2cm，每道记录250个采样点，采样时窗为50ns.通过试验得到电磁波在该球场土壤中的传播速度约为0.09m／ns.在进行偏移前，对该雷达数据进行了去除背景信号及相关噪声处理，结果如图3（b）所示。用相移偏移算法得到的幅度谱和相位谱如图3（c）和（d）所示；用相移偏移与LSMP综合方法进行成像，得到的幅度谱和相位谱分别如图3（e）和（f）所示。可以看出，后一种方法成像结果的背景噪声更弱，同相轴聚焦更好，成像质量明显优于前一种方法。

4 结 论

最小二乘匹配追踪算法具有很强的压制随机噪声的能力，引入NUFFT的相移方法具有较高的精度和计算效率。综合最小二乘匹配追踪算法与相移偏移算法，形成了一种压噪能力很强的快速GPR偏移成像方法，极大地提高了含噪声资料的成像质量。另外，成像结果的相位谱也能较好地反映目标信息。特别是对于含噪声资料，有时相位谱比振幅谱对目标信息的反映更明显。因此，将幅度谱和相位谱进行综合分析，可以更好地识别和圈定目标，这对于低信噪比资料的解释和弱小目标的识别具有重要意义。

［1］CAFFORIO C，PRATI C，ROCCA F.SAR data focusing using seismic migration techniques［J］.IEEE Transactions on Aerospace and Electronic Systems，1991，27（2）：194－207.

［2］LAMBOT S，SLOB E，VAN DEN BOSCH I，et al.Modeling of ground－penetrating radar for accurate characterization of the subsurface dielectric properties［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42（11）：2555－2568.

［3］ODEN C P，POWERS M H，WRIGHT D L，et al.Improving GPR image resolution in lossy ground using dispersive migration［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45（8）：2492－2500.

［4］修志杰，陈 洁，方广有，等.基于F－K偏移及最小熵技术的探地雷达成像法［J］.电子与信息学报，2007，29（4）：827－830.XIU Zhijie，CHEN Jie，FANG Guangyou，et al.Ground penetrating radar imaging based on F－K migration and minimum entropy method［J］.Journal of Electronics ＆Information Technology，2007，29（4）：827－830.（in Chinese）

［5］GAZDAG J，SGUAZZERO P.Migration of seismic data by phase shift plus interpolation［J］.Geophysics，1984，49（2）：124－131.

［6］STOLT R H.Migration by Fourier transform［J］.Geophysics，1978，42（1）：23－48.

［7］张春城，周正欧.基于Stolt偏移的探地雷达合成孔径成像研究［J］.电波科学学报，2004，19（3）：316－320.ZHANG Chuncheng，ZHOU Zhengou.Ground penetrating radar synthetic aperture imaging based on Stolt migration［J］.Chinese Journal of Radar Science，2004，19（3）：316－320.（in Chinese）

［8］LIU Q H，NGUYEN N.An accurate algorithm for nonuniform fast Fourier transform （NUFFT’s）［J］.IEEE Microwave and Guided Wave Letters，1998，8（1）：18－20.

［9］MALLAT S，ZHANG Z.Matching pursuits with time－frequency dictionaries［J］.IEEE Transaction on signal processing，1993，41（12）：3377－3415.

［10］WANG Y.Seismic time－frequency spectral decomposition by matching pursuit［J］.Geophysics，2007，72（1）：V13－V20.

［11］朱 明，普运伟，金炜东，等.基于时频原子方法的雷达辐射源信号特征提取［J］.电波科学学报，2007，22（3）：458－462.ZHU Ming，PU Yunwei，JIN Weidong，et al.Feature extraction of radar emitter signals based on timefrequency atoms［J］.Chinese Journal of Radar Science，2007，22（3）：458－462.（in Chinese）

［12］孙闽红，唐 斌.基于原子分解理论的雷达欺骗式干扰信号特征提取.电波科学学报，2008，23（3）：550－554.SUN Minhong，TANG Bin.Teature extraction of radar deceptive－jamming signal based on atomic decomposition［J］.Chinese Journal of Radar Science，2008，23（3）：550－554.（in Chinese）

［13］HUANG Y Q，LIU Y H，Liu Q H，ZHANG J Z.Improved 3－D GPR detection by NUFFT combined with MPD method［J］.Progress in Electromagnetic Research，2010，103：185－199.

［14］LIU J，MARFURT K J.Instantaneous spectral attributes to detect channels［J］.Geophysics，2007，72（2）：23－31.

［15］GIANNOPOULOS A.GprMax2DV2.0 （Electromagnetic simulator for ground probing radar）［CP／OL］. 2005－10－31 ［2010－06－08］. http：／／www.gprmax.org／download.html.