协同系统鲁棒波束成形算法研究

成文婧 徐玉清 刘兆和 王 欣

（1.总装工程兵科研一所，江苏 无锡214035 2.国防科学技术大学，湖南 长沙410073）

引 言

放大转发（AF）协同波束成形系统，不仅实现简单，而且通过波束成形技术可获得协同分集［1－4］。该技术通过在各中继节点处乘以预先设计的波束成形因子，使得目的节点处获得较好的性能。与一般意义的波束成形问题［5］类似，该技术也是通过预先知道系统的一些信息来优化波束成形向量，以达到一定的优化目标（如目的节点信噪比（SNR）最大化、误码率最小化等）。波束成形系统要求中继节点已知理想信道状态信息（CSI），但是受信道估计误差、量化误差、反馈延迟等因素影响，实际一般不能获得理想CSI。此时根据理想CSI设计的传统波束成形算法性能严重下降。设计对不准确CSI具有鲁棒性的波束成形算法是波束成形技术实用化的关键之一。

传统波束成形设计准则一般有两种：一是在保证目的节点SNR大于某门限的前提下，以最小化中继节点总功率为准则；二是在中继节点功率约束下，以最大化目的节点SNR为准则。不同准则下的波束成形，需要设计对应不同的鲁棒算法。针对第一种准则，文献［6－7］基于最坏情况思想，设计了对应鲁棒算法。其中文献［6］假设中继节点得到的CSI仅在幅度上存在误差，研究鲁棒功率分配算法。文献［7］进一步考虑CSI在幅度和相位上均存在误差，设计了对应鲁棒波束成形因子。针对第二种准则，文献［8－9］也基于最坏情况思想，研究对应鲁棒算法。但是文献［8］仅考虑了第二阶段（中继到目的）CSI存在误差，没有考虑第一阶段（源到中继）信道误差的影响。文献［9］虽然考虑两阶段CSI信息都存在误差，但是只考虑CSI幅度误差，没有考虑相位误差。目前为止，针对获得的两阶段CSI在幅度和相位上均存在误差的情况，最大化目的节点SNR准则对应的鲁棒波束成形算法还没有进行研究。

针对所有中继功率约束（TPC）下以最大化目的节点SNR为准则的协同波束成形系统，设计了对应的鲁棒算法。具体来说，考虑中继节点获得的两阶段CSI存在复误差，基于最坏情况思想，建立了对应保证鲁棒性的优化问题。进而根据扩展S引理和复数矩阵Schur补定理，将此问题由不可解的半无限问题转化为可解的准凸问题，可通过对分搜索算法获得最优解。每次搜索可利用高效的内点算法来判断联合线性约束、二阶锥（SOC）约束和线性矩阵不等式（LMI）约束的凸问题是否可解。仿真表明，提出的鲁棒波束成形算法能够有效抵抗不准确CSI带来的性能损失。

符号表示：（）·′、（）·T、（）·H分别表示取共轭、转置和共轭转置；表示a的模、∠a表示a的相位；⊙表示Hadamard乘积；diag｛w｝表示对角线元素为w的对角矩阵。

1 系统模型

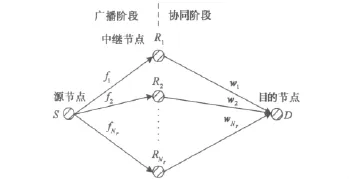
图1 协同场景

考虑由源节点S、目的节点D和Nr个中继节点Ri，i＝1，…，Nr组成的协同系统，如图1所示。各节点均配置半双工的单天线。假设S和D间没有直达路径，由Nr个中继节点协助S与D进行通信。令fi表示S到Ri的信道，wi表示Ri到D的信道，其中fi和wi服从均值为0、方差为1的复高斯分布。假设中继节点对应各信道相互独立，且各节点间达到理想同步。协同过程可分为两个阶段：

1）源节点以功率Ps将符号信息s发送给各中继节点，且满足E｛｜s｜2｝＝1.则中继节点Ri的接收信号为

式中ni表示Ri处的噪声，服从均值为0，方差为1的复高斯分布。

2）Ri对接收信号ri乘以功率归一化因子β＝然后乘以波束成形因子g′i后发送至目的节点。则Ri的发送信号为

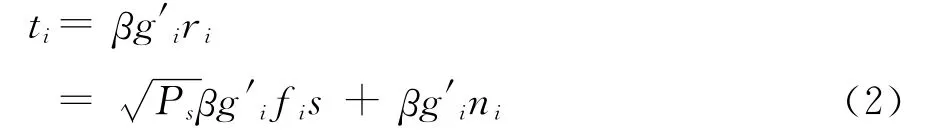
目的节点的接收信号为

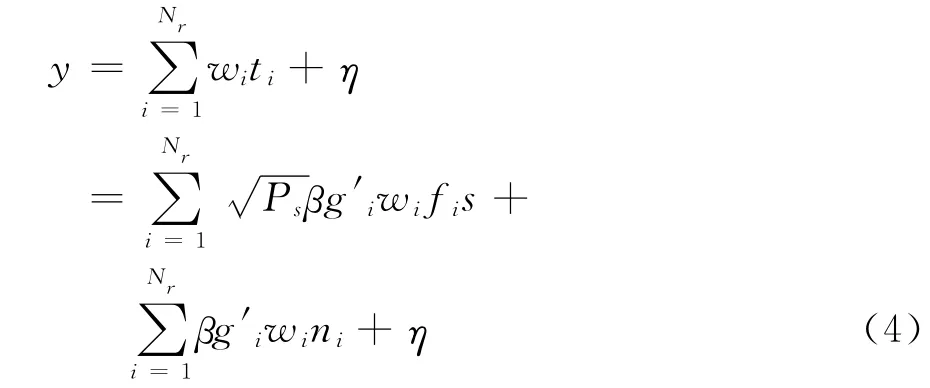
式中，η表示目的节点处的噪声，服从均值为0，方差为1的复高斯分布。

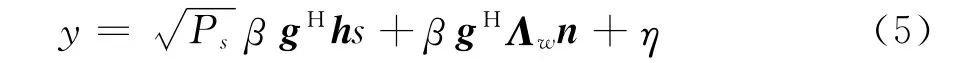
由式（5）可得，目的节点接收信号中的有效信号功率为Psig＝Psβ2gHhhHg，噪声功率为Pnoise＝β2gHΛΛwg＋1，则目的节点接收信号的SNR为

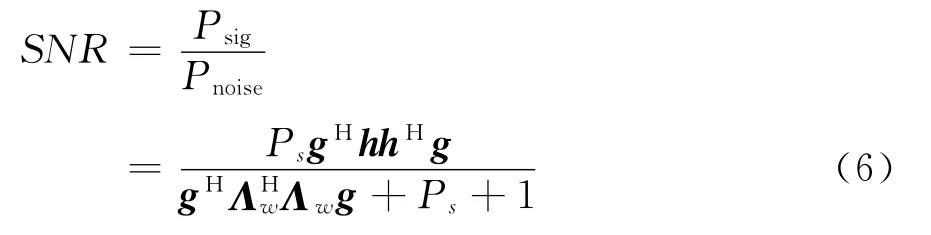
2 传统波束成形设计

假设中继节点的总功率不超过Pmax.由式（3）和式（6）可得，此波束成形设计问题可表示为

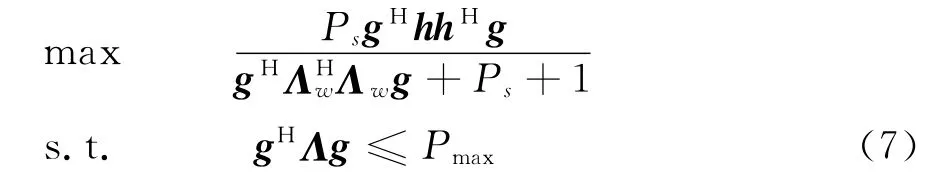
由文献［11］可得，优化问题（7）的最优解为

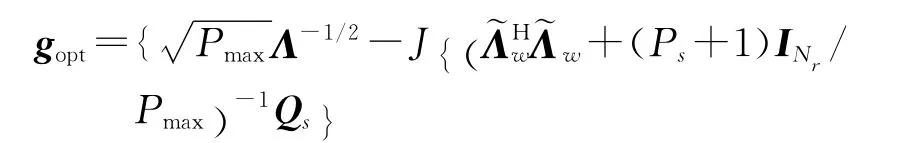
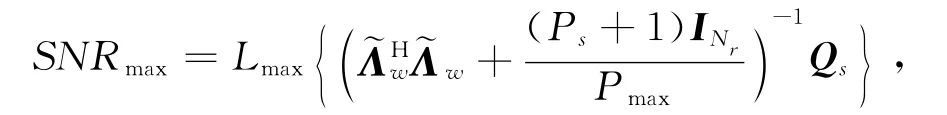
其中Lmax｛·｝表示矩阵的最大特征值。

3 最坏情况下的鲁棒波束成形设计

实际系统中，节点很难获得理想CSI.不准确CSI会严重影响传统波束成形算法的性能。鲁棒波束成形的目的是：合理设计波束成形矢量g，使得当节点得到的CSI存在误差时，仍能获得较好的性能。首先定义信道的不确定集，然后推导鲁棒波束成形因子。

3.1 不确定集建模

假设实际信道向量是在中继节点已知的信道向量上叠加一个复误差向量。此时实际信道所有可能的取值构成信道不确定集，假设为椭圆不确定集：

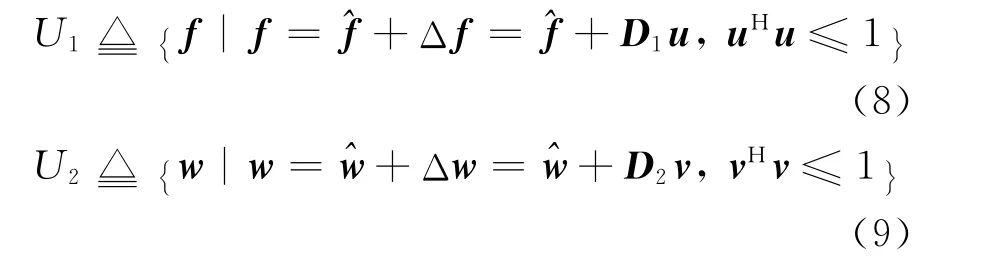
由式（8）可得Λf的不确定集为

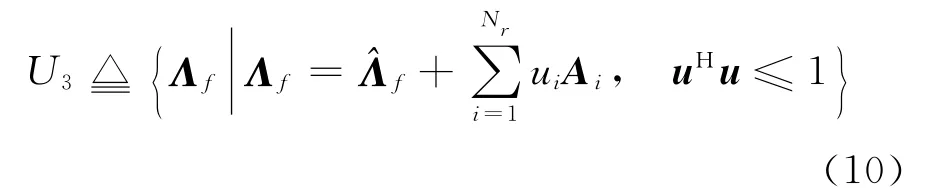
由式（9）可得Λw的不确定集为

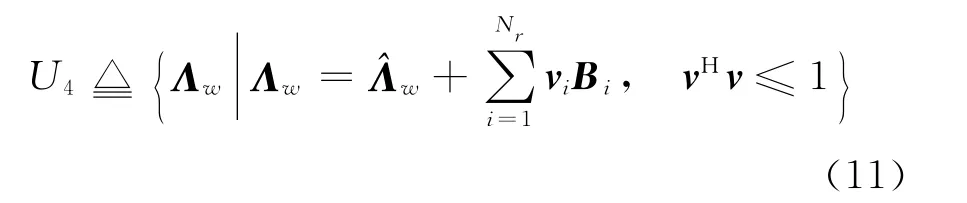
由式（8）和（9）可得

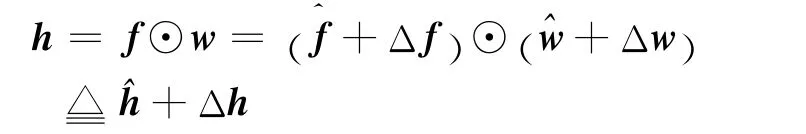
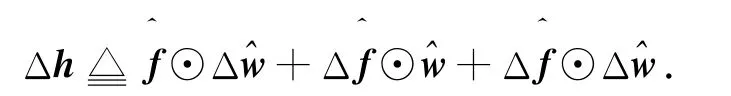
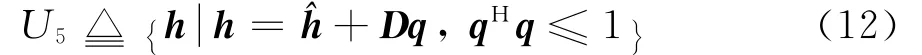
3.2 鲁棒波束成形设计

由于信道的不确定性，TPC下的鲁棒波束成形设计问题不能由第2节的方法得到解析解。

引入辅助变量α，优化问题（7）可等价为

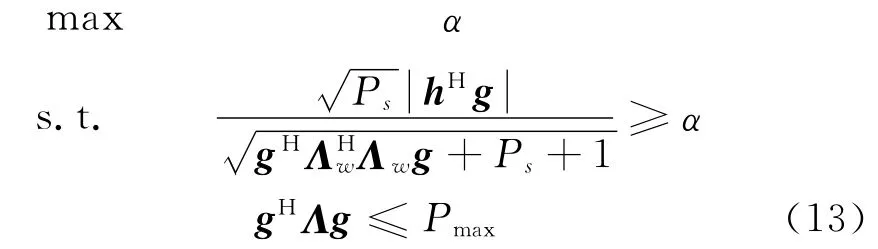
则保证鲁棒性的最优化问题可表示为

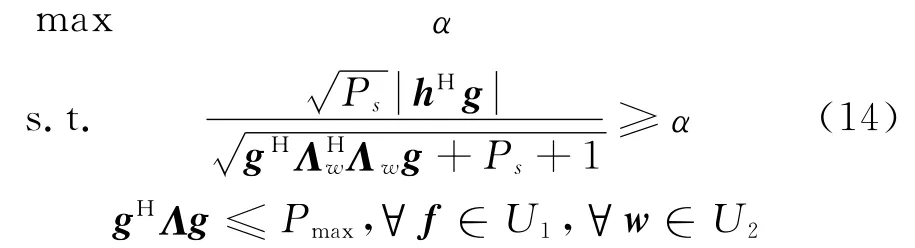
进一步等价为

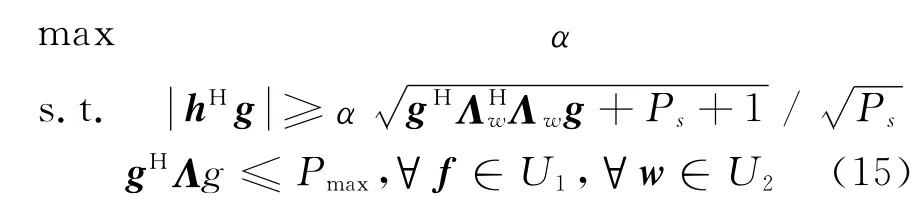
优化问题（15）的最优解即为最优鲁棒波束成形因子。但是不确定集U1和U2中包含无穷个f和w，相当于优化问题（15）中包含无穷个约束条件，难以求解。实际上，要保证不确定集中任意信道都满足约束条件，只要保证最坏情况下满足条件即可。以下我们将基于最坏情况思想，建立新的约束条件，将优化问题（15）转化为可解的凸问题。近似认为优化问题（15）的第一个约束条件的不等式两边涉及的不确定集是独立的［6，9］。引入辅助变量τ≥0，优化问题（15）可等价为

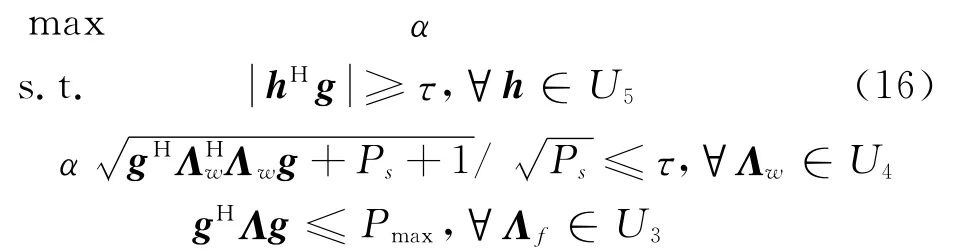
定理：优化问题（16）等价为可解的准凸问题（17）

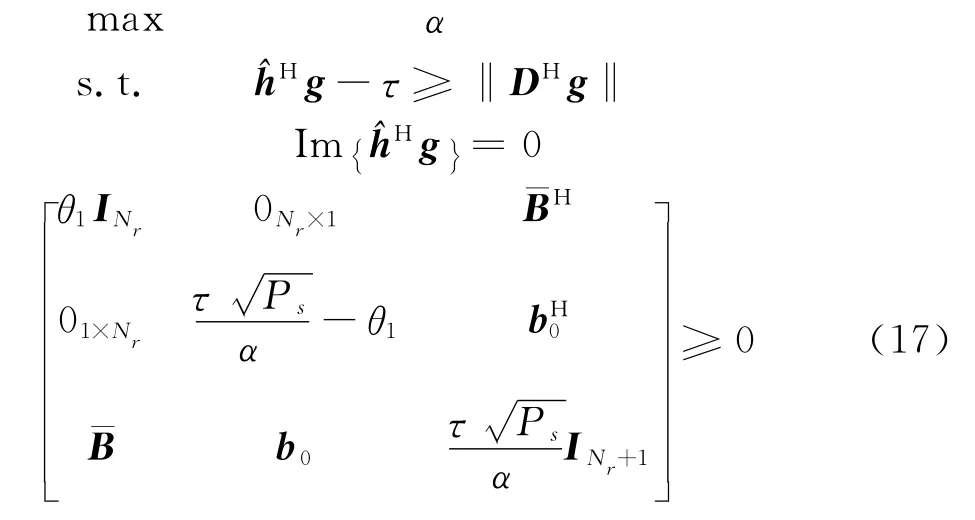
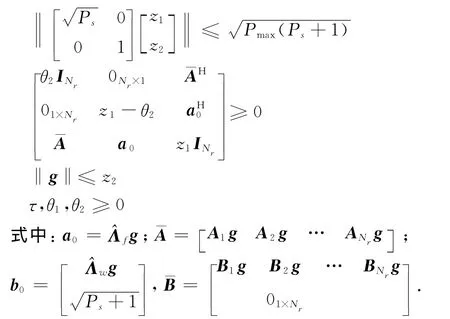
证明：

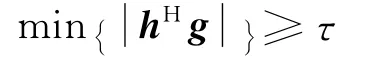
由于qHq≤1，根据Cauchy－Schwarz不等式可得

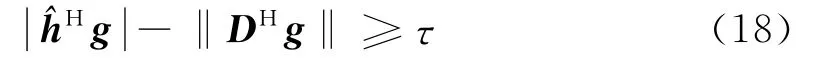
2）第二个约束条件等价为

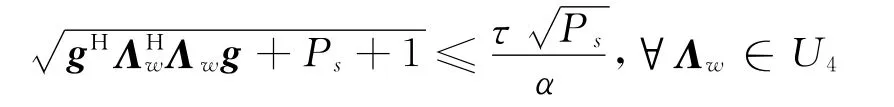
引入范数表示后可等价为

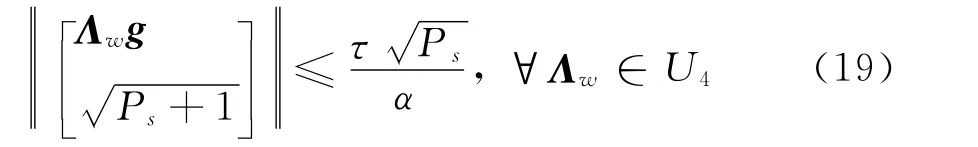
由式（11）可得

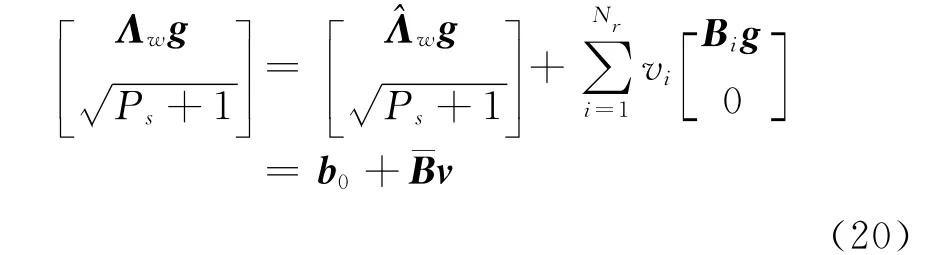
将式（20）代入式（19）中，并根据范数性质‖x‖2＝xHx，式（19）可等价为

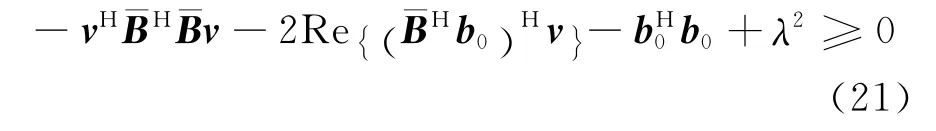
根据扩展S引理（附录A），式（21）成立等价于：存在ρ1≥0，满足

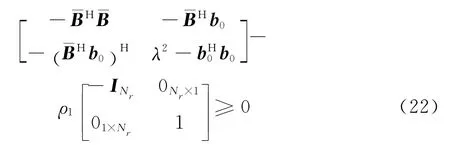
由于ρ1，λ均为非负数，所以一定存在θ1≥0，满足ρ1＝λθ1.则式（22）等价为

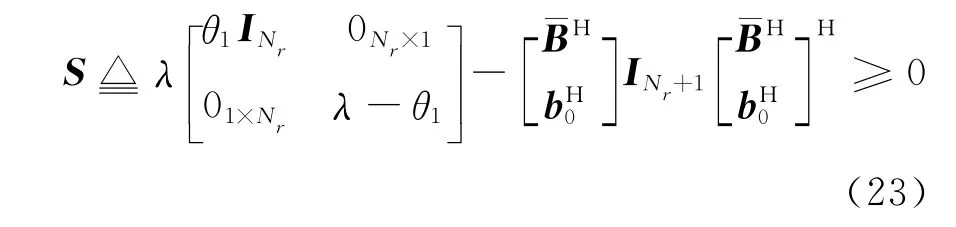
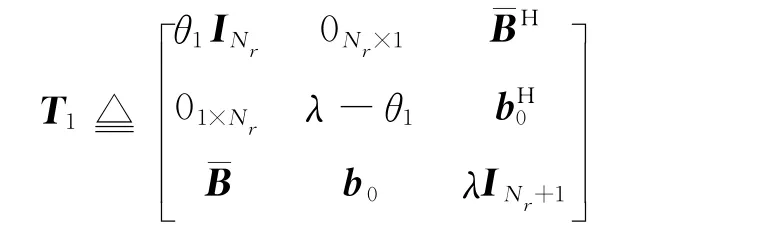
中的Schur补，根据复数矩阵的Schur补定理（见附录B），S≥0等价于T1≥0.

因此第二个约束条件等价为

3）由式（3）可得，第三个约束条件gHΛg ≤Pmax，∀Λf∈U3等价为

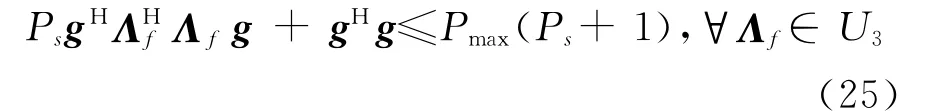
式（25）可等价为式（26）、（27）和（28）的联合

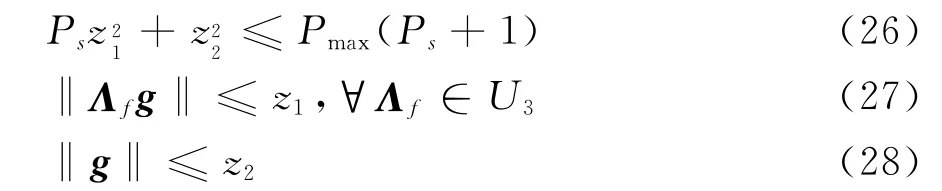
式（26）可以写成二次型的形式，即

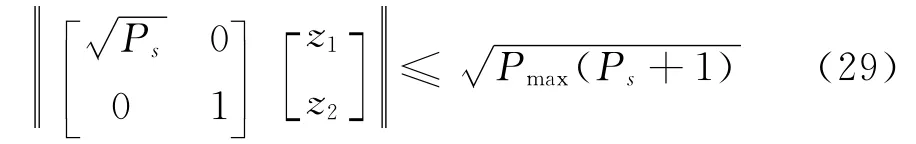
由于式（27）和（19）有着相似的结构，可通过类似的推导，得出式（27）的等价条件为

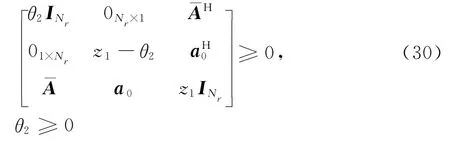
综上所述，式（18），式（24），式（28），式（29）和式（30）为新的约束条件。

由于对g进行旋转，不会影响优化问题（16）的目标函数，也不会影响新的约束条件，所以，可适当旋转g，使得＾hHg为实数。于是有优化问题（16）等价于式（17），定理得证。优化问题（17）的最优解即为最优鲁棒波束成形矢量。该问题为准凸问题［12］，可以通过对分搜索得到最优解。每次搜索需求解一个凸问题［13］，包含4个线性约束，3个SOC约束和2个LMI约束。

4 仿真结果

仿真时取中继数目Nr＝5.为方便起见，取各中继对应的两阶段信道的不准确程度一致，即δi＝εi＝δ，i＝1，…，Nr.对分搜索时取ξ＝1×10－6.

4.1 性能评价

当信道存在偏差时，非鲁棒传统算法设计的波束成形因子对应的节点功率可能大于功率约束。为公平比较算法性能，提出有效信噪比（ESNR）的概念。

定义中断概率为ESNR小于门限γth的概率，即仿真中取γth＝15dBw.

仿真过程如表1所示，取mon和time均为1 000.

表1 仿真过程

4.2 性能仿真

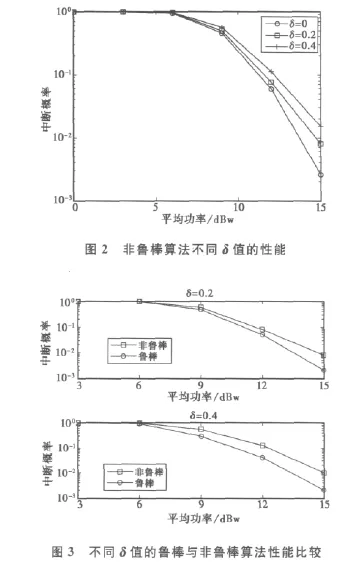
图2为TPC下非鲁棒传统波束成形算法在不同δ值下的中断概率性能曲线。可以看出，当δ＝0.2时，CSI误差对系统性能的影响不能忽略，而且随着δ的增大，CSI误差导致的性能损失更为严重。

图3为δ＝0.2和δ＝0.4时，非鲁棒传统算法和提出的鲁棒算法的性能比较，其中‘非鲁棒’表示中继节点已知的CSI存在误差时，传统波束成形算法根据有误差的CSI设计的波束成形因子对应的性能，‘鲁棒’表示中继节点已知的CSI存在误差时，提出的鲁棒波束成形算法的性能。可以看出，提出的鲁棒波束成形算法能够有效改善CSI误差对系统性能的恶化影响。

5 结 论

所提出的鲁棒波束成形算法，可归结为求解一个准凸问题，应用对分搜索可获得最优解。每次搜索通过高效的内点算法来判断联合线性约束、SOC约束和LMI约束的凸问题是否可解。该算法能够有效降低CSI偏差带来的中断概率性能损失，具有重要的实际意义。

［1］JING Y，JAFARKHANI H.Network beamforming using relays with perfect channel information［J］.IEEE Transaction on Information Theory，2009，55（6）：2499－2516.

［2］PHAM T，NGUYEN H，TUAN D.Beamforming in nonorthogonal amplify－and－forward relay networks［J］.IEEE Transaction on Vehicular Technology，2011，60（3）：1258－1263.

［3］CHENG W，HUANG Q，GHOGHO M，et al.Distributed beamforming for OFDM－based cooperative relay networks under total and per－relay power constraints［C］／／IEEE ICASSP 2011.Prague，Czech Republic，22－27May，2011：3328－3331.

［4］CHEN H，GERSHMAN A，SHAHBAZPANAHI S.Filter－and－forward distributed beamforming in relay networks with frequency selective fading［J］.IEEE Transaction Signal Processing，2010，58（3）：1251－1262.

［5］李洪涛，贺亚鹏，朱晓华，等.基于谱分析的稳健自适应波束成形算法［J］.电波科学学报，2012，27（1）：147－151.LI Hongtao，HE Yapeng，ZHU Xiaohua，et al.Spectral analysis based robust adaptive beamforming algorithm［J］.Chinese Journal of Radio Science，2012，27（1）：147－151.（in Chinese）

［6］QUEK T Q S，SHIN H，WIN M Z.Robust wireless relay networks：slow power allocation with guaranteed QoS［J］.IEEE Journal on Selected Topics in Signal Processing，2007，1（4）：700－713.

［7］UBAIDULLA P，CHOCKALINGAM A.Robust distributed beamforming for wireless relay networks［C］／／IEEE PIMRC 2009.Tokyo，Japan，September 13－16，2009：2345－2349.

［8］ZHENG G，WONG K K，PAULRAJ A，et al.Robust Collaborative－relay beamforming［J］.IEEE Transaction on Signal Processing，2009，57（8）：3130－3143.

［9］QUEK T Q S，WIN M Z，CHIANI M.Robust power allocation algorithms for wireless relay networks［J］.IEEE Transaction on Communication，2010，58（7）：1931－1938.

［10］VOROBYOV S A，GERSHMAN A B，LUO Z Q.Robust adaptive beamforming using worst－case performance optimization：A solution to the signal mismatch problem［J］.IEEE Transaction Signal Processing，2003，51（2）：313－324.

［11］SHAHBAZPANAHI S，GERSHMAN A B，LUO Z Q，et al.Robust adaptive beamforming for generalrank signal models［J］.IEEE Transaction on Signal Processing，2003，51（9）：2257－2269.

［12］BOYD S，VANDENBERGHE L.Convex Optimization［M］.Cambridge：Cambridge University Press，2004.

［13］GRANT M，BOYD S.CVX：Matlab software for Disciplined Convex Programming［Online］.http：／／stanford.edu／boyd／cvx

［14］LI J，STOICA P，WANG Z S.Doubly constrained robust capon beamformer［J］.IEEE Transaction Signal Processing，2003，52（9）：2407－2423.