天波／地波组合传播模式下一阶海杂波特性分析

杨龙泉 凡俊梅，2 蔚 娜 李 星 焦培南，2 李吉宁

（1.中国电波传播研究所，山东 青岛266071；2.电波环境特性及模化技术国家重点实验室，山东 青岛266107）

引 言

在短波频段，电离层反射传播模式、返回散射传播模式和地波绕射传播模式已为大家所熟知［1－2］，也得到非常广泛的研究和应用。如电离层反射传播模式常用于短波通信和广播；天波返回散射传播由电离层传播信道和地海面散射形成，常用于通信和广播监测、雷达等；地波绕射传播模式传播信道主要由不同盐份不同粗糙度的海面绕射形成，常用于近距离通信和广播、短波地波雷达等。

高频探测技术［3－4］对于慢速海面船舶信息的获取是在海杂波背景下完成的，而在海态信息（如风、浪、流等海洋表层动力信息）的反演中，需要准确提取海杂波的信息、依据一定的经验模型进行反演来实现。天波返回散射模式、地波绕射传播模式下的海杂波特性，已经在国内外得到较为充分的研究；基于这两种传播模式的探测技术，在军事和民用上得到了较为广泛的应用。

天波反射／地波绕射组合传播模式是一种新概念的组合传播模式。传播信道主要是时变的电离层反射传播信道和不同盐份不同粗糙度的海面绕射传播信道。显然它是一个组合传播信道，具有复杂的电离层反射传播信道和海面绕射传播信道特性。天波／地波集成探测技术正是基于该组合传播模式来实现的，可用于目标的探测及海洋表层动力环境参数的提取。国内，文献［5］对新组合信道特性及可能应用进行了分析；国外，文献［6］重点论述了天波／地波集成概念，对于舰船探测的限制条件进行理论分析，但没有相关的试验报道。目前，对这种新组合传播模式下的海杂波特性的研究很少。

对天波反射／地波绕射组合传播模式下一阶海杂波的特性进行了研究，通过理论计算分析了海杂波随方位、距离的分布特性及展宽特性，并与获取的实验数据进行对比分析，验证了天波／地波传播模式成立，进而证明实现这种探测技术是可行的，为海面低速目标的检测及海洋表层动力参数的提取提供了理论支持。

1 组合传播模式几何关系及坐标转换

1.1 几何关系

高频段无线电波通过自由空间斜入射到电离层，经电离层反射后通过自由空间到达地（海）面，再经地（海）面以表面波形式传播到接收点。

图1中TT为天波发射站，RR为地波接收站，S点为海面某散射点，P0、P分别是经电离层反射到达地波接收站RR、S点的天波路径，其对应的地面大圆距离为D0、D，S点到接收站的距离为Rr；β为双基地角，γ为入射电波擦地角，组合传播模式下距离的换算方法要比单基地和双基地高频雷达的复杂。

1.2 坐标转换

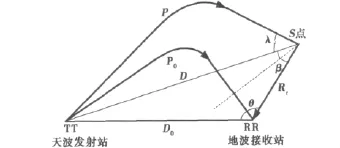
图1 几何示意图

系统得到的群路径实际上是电波射线在自由空间、电离层及海洋表面传播时间的度量，由这种群路径无法得到其实际位置，必须将其转换成实际对应的地面距离。

系统可以测得的S点方位角为θ，测得S点对应总路径为R＝P＋Rr，D0为发射站到接收站基线距离，这三个参数是已知的，求解Rr.

设P和D差值为Δ，即

可得平面坐标下定位方程［7］为

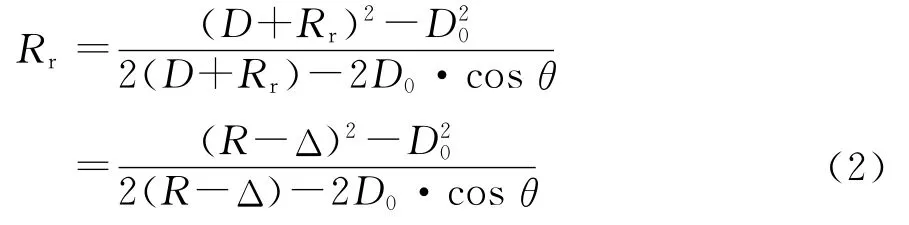
在电离层状态已知的情况下，可以获得方位角θ方向上其每个距离单元Rri（i＝0，1，2，3，…，表示第i距离单元）对应的P 和D 差值Δi（i＝0，1，2，3，…）再结合方程（2）用迭代方法得到S点实际位置。

在海面散射单元S位置确定的情况下，平面坐标下对应的双基地角β、入射电波擦地角γ可由式（3）和（4）表示为

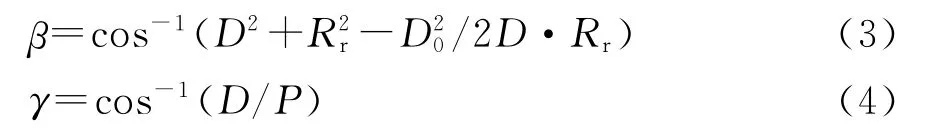
2 组合传播模式下一阶海杂波特性

不同于天波返回散射、地波绕射探测海洋回波后向散射情况，组合模式下一阶海杂波呈现出一些不同特征如一阶海杂波频移分布、展宽特性以及传播路径的损耗特性。

2.1 组合信道下一阶海杂波频移的导出

高频雷达的海杂波由一阶、二阶及高阶分量组成，其中一阶海杂波包含两个对称的尖峰即正负一阶Bragg峰。其作用机理可用Bragg谐振散射过程解释，入射无线电波与海浪作用引起无线电散射，由于散射回波是高频电波与海浪一次作用引起的，因此，这一过程称之为高频电波与海浪一阶作用。当海浪波长与无线电波波长满足Bragg谐振条件时，则发生 Bragg谐振散射［8－12］。

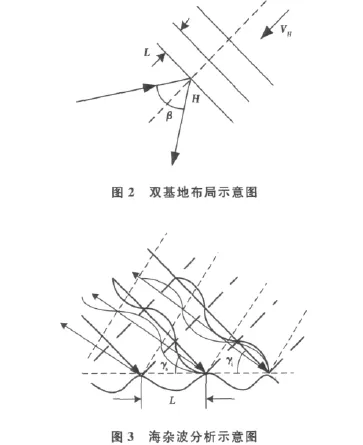
双基地布局见图2，H位置处的海浪波长为L，相速度为VH，方向沿双基地角平分线方向。图3为海杂波分析示意图，入射电波擦地角为γi，散射电波擦地角为γs.

海浪Bragg谐振散射条件为

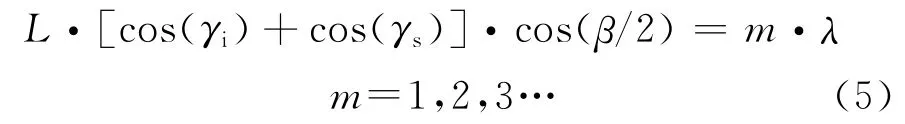
当m＝1时，即为一阶海杂波，式中λ为无线电波波长。在天波发射／地波绕射组合传播模式下，其海浪散射回波路径为地波绕射传播方式，此时，γs＝0°，因此，由式（5）可以导出天波／地波组合传播模式下一阶海杂波谐振条件为

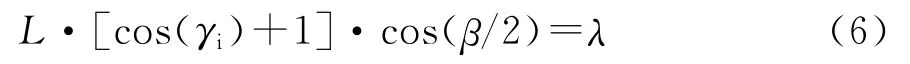
则由海浪运动引起的多普勒频移为

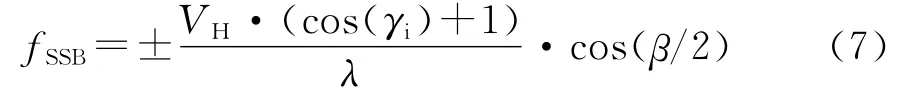
对于重力波浪，结合式（6），其特征速度与其波长有下列关系

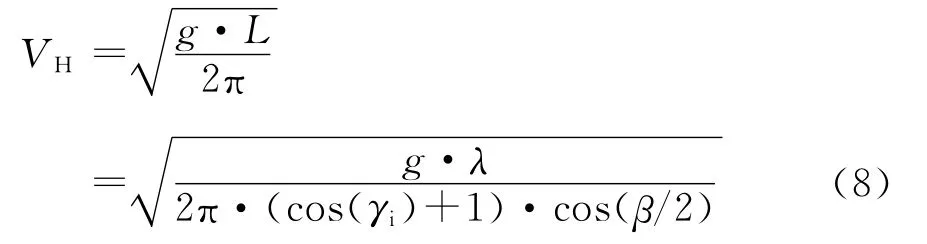
将式（8）代入式（7），考虑电离层的影响，忽略海流的影响，可导出天波反射／地波绕射组合传播信道下的一阶海杂波频移为

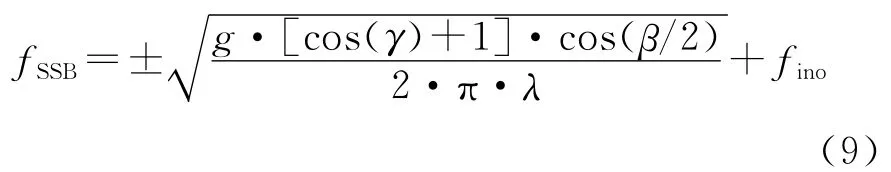
式中：双基地角β及擦地角γi是方位、距离的函数；fino为电离层运动引起的多谱勒频移。因此，组合传播模式下的一阶海杂波频移是频率、方位、距离和电离层的函数。

2.2 一阶海杂波展宽特性分析

天波／地波联合传播模式包含了电离层反射、地波绕射，发射站、接收站为双基地布局，其一阶海杂波频谱是频率、方位、距离、电离层的函数（见式（9））。因此，导致一阶海杂波谱展宽的主要原因有两种：其一，组合传播模式下，入射电波经一次电离层反射，电离层随机运动、电离层多模传播导致一阶海杂波谱展宽；其二，双基地特征导致一阶海杂波展宽，在一定接收波束宽度内，同一射线距离回波对应的双基地角不同，导致海杂波谱展宽。

重点分析系统双基地特征导致海杂波展宽原理及影响程度。一般，地波接收系统通过天线组阵来完成测角功能；接收波束的宽度取决于天线阵列的口径大小。在一定波束宽度内，同一射线距离内各散射单元对应的双基地角β不同，各单元海浪散射回波信道多普勒频移不同，进而导致一阶海杂波的展宽。

图4在一定接收波束宽度dθ范围内，同一射线距离R上，方位范围边界上S1、S2散射单元对应的双基地角分别为β1、β2。D1、D2、Rr1、Rr2分别为S1、S2散射单元距离天波发射站、地波接收站的地面距离。S1、S2散射单元对应的方位角分别为θ＋dθ／2、θ－dθ／2.

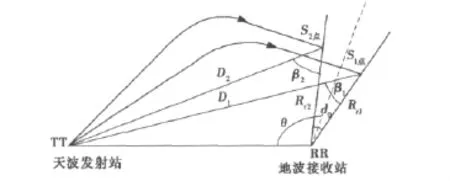
图4 同一距离不同双基地角单元散射示意图

在散射单元S1、S2群路径（射线距离）、方位角、收发站间距离已知的情况下，利用式（2）可以得到D1、D2、Rr1、Rr2，进而代入式（3）可以得到对应的双基地角β1、β2.

在忽略海流情况下，正负一阶海杂波频率的最 大可能范围可表示为

3 计算实例

利用上述分析方法，设定条件，对天波反射／地波绕射组合模式下一阶海杂波随距离、方位的分布特性以及海杂波谱展宽特性进行理论计算分析。

3.1 一阶海杂波谱展宽

设定条件：接收站距发射站800km，频率为10 MHz，波束宽度为20°，忽略电离层对海杂波展宽的影响。由式（10）计算300km（距接收站的实际距离）范围内、不同方位上海杂波展宽量，其中，同一射线距离不同方位上的双基地角β、擦地角γ由式（2）～（4）得到。计算结果见图5.

图5显示了一阶海杂波展宽随距离、方位的变化特性：在方位角θ较小时，即对应的双基地角大，一定接收波束宽度内，海杂波展宽较严重；在方位角θ较大，接近180°时，一阶海杂波的展宽很小，与单基地情况类似。

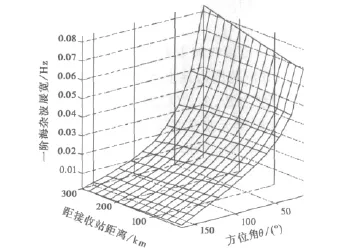
图5 一阶海杂波频谱的展宽特性

船舶慢速目标检测主要以海杂波为背景，一阶海杂波谱展宽会恶化检测背景。一般来说，一阶杂波展宽达到2倍频率分辨率以上时，才能对目标检测带来影响；通常，受电离层传播影响，相干积累时间取50～100s，对应频率分辨率为0.01～0.02 Hz.因此，在系统平台设计时，其接收波束与收发站间基线夹角θ宜控制在合适范围。

3.2 一阶海杂波频移理论分布特性

设定条件：地波接收站距天波发射站800km，工作频率为10MHz，假定能够探测到一阶海杂波谱的实际距离（距地波接收站）为200km范围，计算典型方位指向上（θ＝30°，60°，90°，120°，150°）一阶海杂波频谱的分布特性，计算结果见图6.

图6 一阶海杂波频谱的分布特性

实际回波信号除海杂波信号外，还包含经电离层一次反射而被地波接收站所接收的电离层直达波信号，为分析方便，定义电离层直达波信号距离为基准距离（即零距离），海洋回波的群距离可表示为射线距离与电离层直达波信号群距离之差（即RP0）。

图6显示，典型方位指向上一阶海杂波分布特性有以下特点：

1）一阶海杂波的相对群距离随方位角的增加而增加，逐渐接近单基地后向散射的情况；在方位角较小时，会导致回波的距离分辨力变差。

2）随群距离增加，一阶海杂波频移逐渐增大。

3）随方位角增大，相应双基地角减小，一阶海杂波频移增大，逐渐接近单基地后向散射情况。

4 实测信号与理论计算结果对比分析

利用系统的天波发射设备和地波接收设备进行了海洋回波谱检测试验，获取了实测数据。试验平台设置：接收站、发射站相距800km，接收天线法线指向与收发站间基线夹角θ为56.2°.探测参数设置：信号形式为线性调频连续波，频率为10.4 MHz，带宽为40kHz，重复周期为20ms.相干积累时间为51.2s.

数据的处理过程包括脉冲压缩、波束合成、相干积累等过程，得到不同方位指向上距离－多谱勒－幅度的频谱图。

4.1 一阶海杂波频谱分布特性实验分析

图7为一组天波反射／地波绕射组合传播模式下距离－多谱勒－幅度的实测回波频谱图，纵坐标（群距离）以电离层直达波信号为基准距离（即零距离），图中0km、0Hz附近为电离层直达波信号。红色虚线为各方位指向上的一阶海杂波分布的理论计算值，其中扣除了电离层引起的频偏。

由图7可以得到：

1）实测信号一阶海杂波的频移与理论计算值相符合，随群距离的增加呈现出增大的趋势。

2）实测海杂波信号对应群距离随方位角的增加而逐步增大，理论分析现有布局下海杂波群距离随方位角增大而增大，实测海杂波信号的方位变化特征与理论分析相符合。

3）实测信号的正一阶海杂波信号幅度大于负一阶，该时段风向为西北风，朝向双基地角平分线方向，这种情况对应正一阶峰幅度大。

通过对实测一阶海杂波信号特征与理论计算的对比分析，进一步证实处理得到的信号就是天发地收联合模式下一阶海杂波信号，验证了天波反射／地波绕射组合传播模式的概念是成立的。

4.2 一阶海杂波展宽特性实验分析

图8、9为方位20°波束指向（即θ＝76.2°）相对群距离单元39km（对应实际距离Rr约为31km）、132km（对应实际距离Rr约为112km）处的一阶海杂波多普勒－幅度图（相干积累时间为51.2s，对应多谱勒分辨率为0.019 5Hz）.在两图中可以看到明显的正负一阶海杂波；箭头所指的竖直红色虚线表示半功率波束宽度下同一射线距离不同双基地角引入的正、负一阶海杂波谱展宽量；水平红色虚线为一阶海杂波峰值以下3dB位置。

两图中实测一阶海杂波谱3dB展宽占据了近两个频率分辨率单元，要大于半功率波束内双基地角引入的展宽量理论计算值。实测一阶海杂波信号20dB展宽占据了6～8个多谱勒分辨单元，约0.12～0.15Hz频率展宽，远比单基地地波雷达展宽严重，导致慢速目标检测背景恶化。分析其原因有：

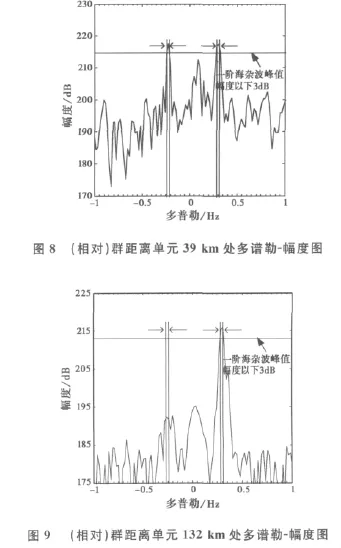
1）实验平台布局及波束宽度过大导致杂波频谱展宽严重，接收波束与收发基线夹角θ在36.2°～76.2°，相应的双基地角过大；发射为宽波束，接收天线阵列孔径又较小，10.4MHz频率上主瓣20dB波束宽度在40°以上。各方位上同一射线距离不同双基地角的海杂波信号引起杂波频谱的展宽。因此，可以通过减小双基地角、降低波束宽度等措施来抑制杂波频谱展宽。

2）电离层的影响，海洋回波信号要经过电离层传播的调制，该组数据对应的电离层反射传播直达波信号也出现了一定程度的展宽，如对应的电离层直达波信号3dB展宽占据了约1.3个多谱勒分辨单元，20dB展宽占据了约3.8个分辨单元。因此，可以通过选择电离层污染小的工作频率等措施来抑制杂波频谱展宽。

5 结 论

本文分析了天波反射／地波绕射组合模式下一阶海杂波的发生机制，导出了一阶海杂波频移的计算公式；分析了组合模式一阶海杂波展宽原理，并推导了由双基地布局引入的一阶海杂波展宽计算公式。利用推导的一阶海杂波频移、展宽计算式，结合几何关系换算计算公式，仿真计算并分析了组合模式下一阶海杂波频谱随距离、方位的分布特性及展宽特性，得出了一些较为有意义的结论。

最后，对实测一阶海杂波信号频谱特征与理论分析结果进行了对比分析，实验结果与理论分析相符合，进一步证实处理得到的信号就是天发地收联合模式下一阶海杂波信号，验证了天发地收联合模式集成概念成立探测原理可行。本文对一阶海杂波特性所做的理论与实验研究的分析结果，对该探测技术的平台布局设计以及在船目标、海态信息监测等方面的实际应用，具有十分重要的参考意义。

［1］江长荫，张明高，焦培南，等.GJB／Z 87－97雷达电波折射与衰减手册［S］.北京：国防科工委军标出版社，1999.

［2］焦培南，张忠治.雷达环境与电波传播特性［M］.北京：电子工业出版社，2007.

［3］斯科尼克.雷达手册［M］.王 军，译.北京：电子工业出版社，2003.

［4］周文瑜，焦培南.超视距雷达技术［M］.北京：电子工业出版社，2008.

［5］焦培南，杨龙泉，凡俊梅.短波天波反射／地波绕射组合新传播模式及其可能应用［J］.电波科学学报，2007，22（5）：745－750.JIAO Peinan，YANG Longquan，FAN Junmei.New propagation mode associate with HF sky－surface wave and its application［J］.Chinese Journal of Radio Science，2007，22（5）：745－750.（in Chinese）

［6］RIDDOLLS R J.Ship Detection Performance of a High Frequency Hybrid Sky－Surface Wave Radar［M］.Ottawa：Defence R＆D，2007.

［7］杨龙泉，焦培南，凡俊梅.短波天波／地波联合传播模式下定位方法研究［J］.中国电子科学研究院学报，2010，25（3）：311－314.YANG Longquan，JIAO Peinan，FAN Junmei.A study on algorithm for the target localization in the hybrid sky－surface wave mode［J］.Chinese Journal of Radio Science，2010，25（3）：311－314.（in Chinese）

［8］BARRICK D E.First－order theory and analysis of MF／HF／VHF scatter from the sea［J］.IEEE Transaction on Antennas and Propagation，1972，20（1）：2－10.

［9］LARSON R W.Bistatic clutter measurements［J］.IEEE Transaction on Antennas and Propagation，1978，26（6）：801－805.

［10］KHENCHFA A，DAOUT F，HURTAUD Y，et al.Bistatic sea clutter simulations and measurements［C］／／Geoscience and Remote Sensing Symposium.Lincoln，27－31May，1996：615－617.

［11］TRIZNA D，GORDON J.Results of a bistatic HF radar surface wave sea scatter experiment［C］／／Geoscience and Remote Sensing Symposium，2002，3：1902－1904.

［12］WANG J，DIZAJI R，PONSFORD A M.Analysis clutter distribution bistatic high frequency surface wave radar［C］／／Canadian Conference on Electrical and Computer Engineering，May 2－4，2004，3：1301－1304.