基于矢量天线的新型三维调制解调方法

宋汉斌 陈晓光 张建秋

（复旦大学信息科学与工程学院，上海200433）

引 言

调制解调技术是通信系统中的一项关键技术，它关系到信息传输的速率和误码性能。这也意味着，在通信系统中引入速率更快、性能更好的调制解调技术就成为提高或改善系统性能的途径之一，其中扩展调制解调信号的维度是提高调制解调性能的直接方法。近年来，人们对如何将二维调制解调扩展到三维调制解调开展了一系列研究。例如：在光通信系统中，人们利用光的偏振（极化）信息对光信号的三维调制解调进行了研究［1－5］。那么，在无线通信领域中，能否也可以在传统标量调制的基础上，引入新的变量来实现多维的联合调制解调呢？

极化参数是描述空间电磁场的重要参数之一，人们通过引入双极化天线，以极化分集代替空间分集进行接收，使接收信号的增益提高了3dB，这表明，合理利用电磁波的极化信息，可提高无线通信系统的性能［6］。在二三十年代，人们就展开了在调幅（AM）广播中使用电磁波的极化信息进行调制的研究，并指出极化调制可以获得较高的载噪比。但是，传统的极化调制中通常使用与地面平行或者垂直的天线进行发射与接受，调幅广播通常采用垂直极化的发射方式，而电视信号通常采用水平极化的发射方式，这种极化调制只利用了相互正交的载波将信号进行叠加，使原有的双边带信号变为单边带信号，而信息传递始终是通过改变电磁波信号的幅度与相位来完成的，在信息传输的过程中，并没有利用电磁波本身的极化参数来传递信息。在无线通信系统中，我们是否能够利用电磁波的全部极化信息，进行三维联合的调制解调呢？据作者所知，目前在无线通信系统中所开展的三维联合调制的研究还比较少。文献［7］指出，矢量电磁波的幅度、极化与相位等变量都可以作为未来联合调制的参数。因此，希望在传统的标量幅度和相位调制的基础上，引入新的变量来携带信息，在无线通信中实现三维联合调制解调。矢量电磁波的极化参数就是这种新的变量之一。

近年来，随着矢量天线的发展，为利用电磁波的极化信息提供了新的思路［8－9］。美国发明专利［8］发明了由6根有向天线构成的电磁矢量天线。这6根有向天线分别是在三维空间中相互正交的3个方向上的电性天线，以及相互垂直的3个方向上的磁性天线。文献［9］报道了电磁矢量天线的实验室实现方法。这种电磁矢量天线可以完整地记录三维空间中电磁波所携带的三维电场和三维磁场信息，同时，它还具备了传统标量天线所不具有的性质。例如，接收端可以在不知道具体阵列结构的情况下，对空间电磁源的波达方向（DOA）和极化参数进行估计［10－11］；矢量天线的应用可以提高到达角的估计精度［12］。这些研究均表明：将电磁波的几何特性和天线几何结构相结合的电磁矢量天线的出现，使人们发现了许多以前未知的现象和规律［13－14］。

借助于矢量天线对电磁波极化信息敏感的特点，提出了一种无线通信中用矢量天线将信号相位、极化幅度与极化俯仰角进行三维联合调制的新方法，该方法利用矢量传感器发射携带有极化信息的载波，在接收端同样利用矢量天线进行接收并解调，可以同时获得原有的相位调制信息和极化调制信息，具有传输速率高、误码率低的特点。本文阐述了如何实现联合极化与相位调制，描述了调制信号的接收与解调方法，给出了联合极化与相位调制解调的系统框图和三维空间星座图，并对其误码率进行了仿真，给出了相关结论。

1 联合极化与相位信号的调制

矢量天线由三个电偶极子和三个磁偶极子构成，它们在空间上相互正交、同点分布，且具有不同的极化特性，能够发射和接收x、y和z三个方向的电场和磁场分量，典型的矢量天线如图1所示。

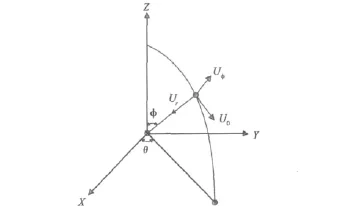
图1 矢量天线极化－角度导向矢量方向图

文献［7］指出，对于远场信号，原点O处矢量天线x、y和z三个方向所接收到的电场信号可以表示为

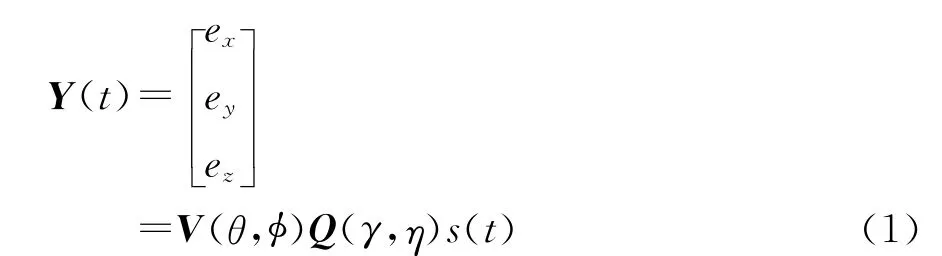
式中：ex、ey和ez分别表示矢量天线在x、y和z三个方向的电偶极子上感应到的电场分量；V（θ，φ）与电磁波相对于矢量天线的波达方向有关，其可以表示为

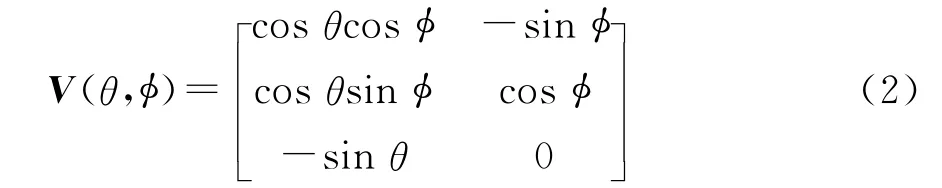
其中：θ∈［0，π）表示信号的俯仰角，即z轴与入射信号方向之间的夹角；φ∈［0，2π）表示信号的方向角，即从x轴沿逆时针方向旋转到信号入射方向在x－y平面投影的夹角。Q（γ，η）矢量电磁波的电场极化方向有关，其可以表示为

式中：γ表示矢量电磁波的辅助极化角；η表示矢量电磁波的极化相位差异角。s（t）是天线发射电磁波信号的复表示，即

文献［7］在得到了式（1）所示的矢量电磁场表达式后，认为电磁场的幅度、极化和相位等参数均可以用来传递信息，并指出，联合这些参数的矢量调制方式是未来调制解调的研究方向之一。然而，文献［7］中未讨论如何利用这些参数进行调制的方法。同时，文献［7］中也没有给出与多维调制相适应的具体的解调方法。式（1）给出了描述矢量电磁场各个参数之间关系的方程，从这一方程出发，结合矢量天线对极化信息敏感的特点，找到一种多参数的联合矢量调制方法，给出其调制信号的矢量表达式和三维星座点的排布方式，并将给出矢量天线所接收到三维调制信号的解调方法。

仍然使用图1中的x，y和z来表示三维空间直角坐标系中的单位方向矢量，以φ，θ和－r来表示TME波传播方向的单位矢量，则全极化TEM波的电场分量可以表示为［15］

式中：Eφ表示TEM波的水平极化分量；Eθ表示TEM波的垂直极化分量。在给定极化模式的情况下，TEM波φ和θ方向电场分量的幅度‖Eφ（t）‖和‖Eθ（t）‖可以表示为［15］

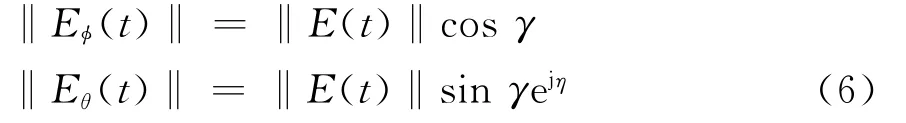
其中‖E（t）‖表示横向电磁波（TEM）波的幅度。需要说明的是，电磁波在传播方向－r方向上电场分量为0.结合式（4）、（5）和（6），当信号的复幅度恒定时，可以将TEM波θ和φ方向的电场信号E表示为

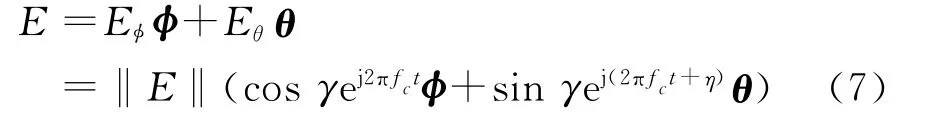
考虑具有如下形式的相移键控（PSK）调制波形符号sm（t）

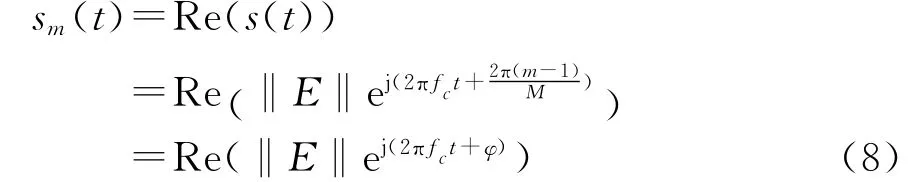
式中：s（t）表示无线通信中传输的复信号；Re（·）表示取实部运算；fc表示载波频率；φ表示调制信号的相位；‖E‖表示调制信号的幅度。PSK调制通过控制调制信号的相位来传递信息，其星座图是二维星座图。我们希望在传统的PSK调制中引入新的调制参数，从而将传统的PSK信号进行扩展，实现三维联合调制。文献［6］中指出，合理地运用电磁波的极化信息可以有效提高通信系统的性能，因此，引入电磁波信号的极化参数作为新的调制变量，来实现电磁波极化与相位的三维调制，即使用全极化TEM波作为载波信号来进行调制。将式（5）中描述的全极化波以复信号的形式带入式（8），可以得到新的极化与相位三维联合调制的信号，其表达式为

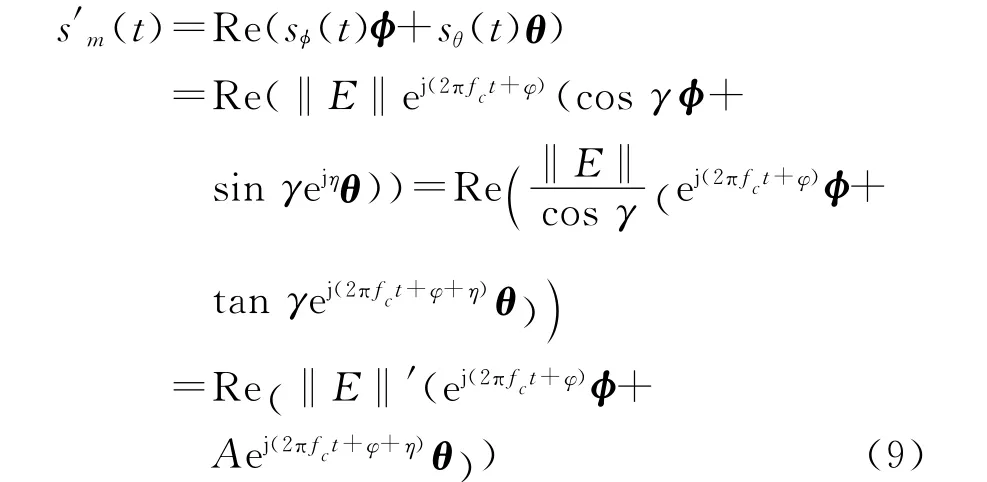
式中：sφ（t）和sθ（t）分别表示水平极化方向和垂直极化方向的复信号；fc表示载波频率，‖E‖′＝‖E‖／cosγ表示三维调制信号的归一化能量；A＝tanγ为水平极化方向与垂直极化方向电场分量幅度的比值；φ为PSK调制相位；η为信号的极化相位差。也就是说，A和η表达了调制信号的极化信息，φ表达了调制信号的相位信息。这样，可以通过控制A，φ和η这三个独立参数来传递信息，实现联合极化和相位的三维调制，并称其为poPSK调制（极化PSK调制）。此时，式（7）中所示的矢量天线x、y和z方向电偶极子上的复信号可表示为

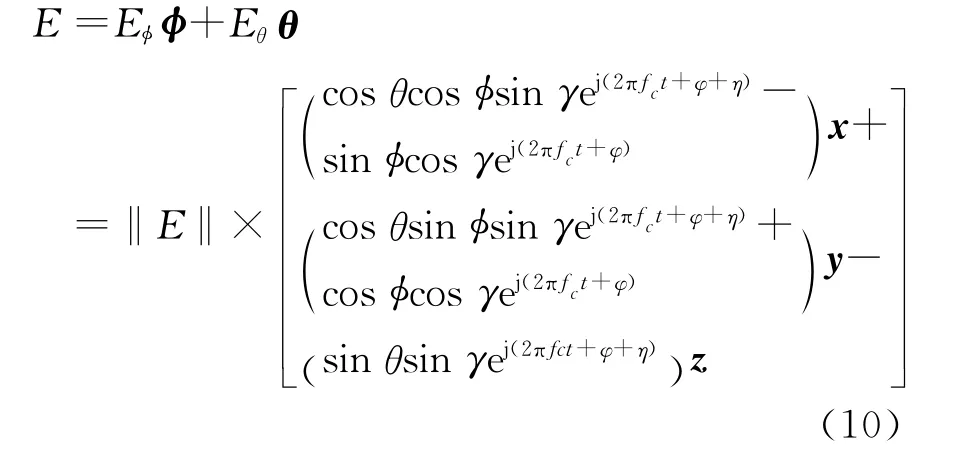
2 三维调制信号的解调

在单信号源发射、单矢量天线接收的情况下，接收端采用图1所示的矢量天线接收全极化TEM波信号，矢量天线的x、y和z三个方向的电偶极子上能够分别接收到发射端所发出TEM波在x、y和z三个方向的电场分量。当波达方向角为（θ，φ）时，矢量天线接收到的电场信号可表示为

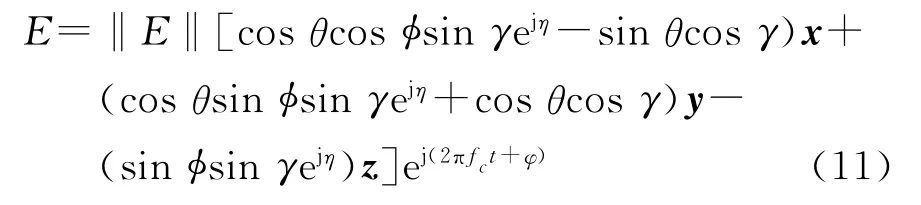
在微波中继传输过程中，可以通过调整接收天线的角度，使其x、y和z轴与发射天线的x、y和z轴对准。此时，天线z轴的方向即为电磁波的传播方向，于是有θ＝0，φ＝0.此时式（11）可化简为

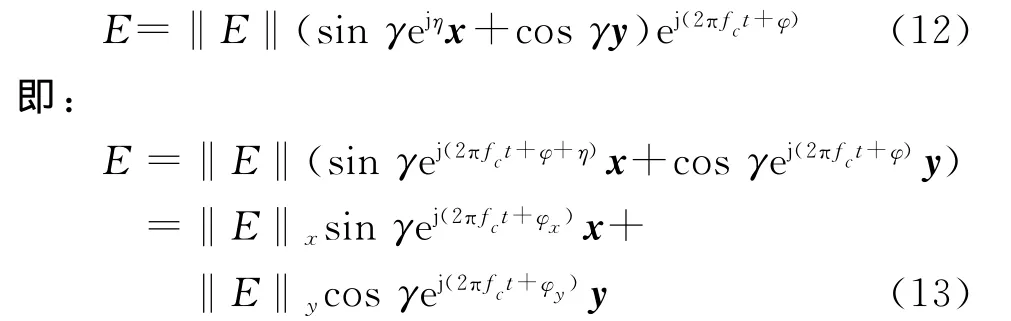
式中：‖E‖表示电磁波的幅度；‖E‖x和‖E‖y表示矢量天线x和y方向电偶极子接收到电场信号的幅度；φx和φy表示矢量天线x和y方向电偶极子接收到电场信号的相位。在解调过程中，采用包络检波或者最大似然的检波方法［16］，分别检测出x方向和y方向电场信号的幅度‖E‖x和‖E‖y.根据poPSK调制中各参数的物理意义，可知‖E‖x和‖E‖y的比值为tanγ，即三维极化和相位调制中的调制参数A，满足

在x和y方向分别利用相干解调方法，将归一化之后的信号分别乘以cos 2πfct和sin 2πfct，再经过低通滤波即可得到φx和φy的值，采用差分编码可以消除可能存在的相位模糊。其中，y方向电偶极子接收到信号的相位φy即为联合极化和相位的三维调制中的调制参数φ；x和y方向信号的相位差φx－φy即为联合极化和相位的三维调制中的调制参数η.

这样，就恢复出了三维极化和相位调制的三个参数A、φ、η，在得到这三个参数之后，通过三维星座图的映射就能解调出原始数据信息。

3 三维联合调制系统框图与信号星座图

无线通信较光纤通信会存在空间电磁波的干扰，应该如何克服这些干扰对极化与相位三维联合调制带来的影响呢？在环境比较空旷，高度比较高的高空，空间电磁场比较稳定，此时电磁波受到干扰和多径衰落的影响都比较小，且电磁波干扰变化的速度比较缓慢。而微波中继通信和卫星通信的信道环境恰恰满足这两个特点。于是，在信号传输过程中，每隔一段时间间隔就插入一段固定的导频信号，由于高空电磁场变化缓慢，因此，可以认为每个时间段内的电磁场是稳定的。导频信号可以为极化相位的联合调制解调提供一个初始值，用来修正空间电磁场干扰对调制信号带来的影响。三维极化和相位调制解调的系统框图如图2所示。

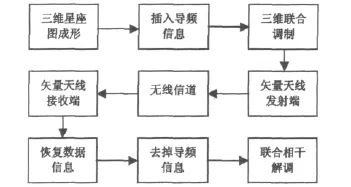
图2 三维联合调制解调系统框图

三维调制是通过三个独立参数来传递信息的，显然，二维坐标不能表示三个独立参数，因此，在球坐标系中以A为半径，以φ和η为两个角度来确定星座点的坐标（A，φ，η），以便在三维球坐标系中画出poPSK调制的三维星座图。

在联合极化和相位的三维调制中，令θ方向的信号总小于φ方向的信号，则有0＜tanγ＜1.这样，便可将所有星座点归一化到半径为1的球面之内。A相同的信号，在星座图中分布在同一个球面上；φ∈［0，2π）代表信号的相位调制分量，即星座点投影在x－y平面后与x轴的夹角，与PSK信号中星座点的意义相同；η∈［0，π）代表信号的极化方位角，即信号与z轴的夹角。以4－poPSK调制、6－poPSK调制和26－poPSK调制为例，其星座图如图3所示。

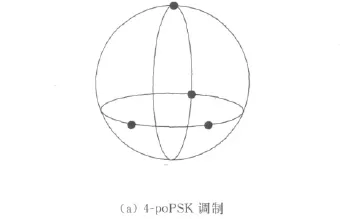
通过引入极化参数作为新的调制变量，实现了联合极化和相位的三维调制。其星座图也从传统的二维调制解调星座图，扩展到了三维立体调制解调星座图。星座图中相邻星座点之间的最小欧氏距离代表着信号误码率的大小，在星座点数量相同的情况下，由于分布在三维空间的poPSK信号较二维空间的PSK信号能够获得更大的欧式距离，因此，它具有更小的误码率，或者说，当分布在三维空间中的poPSK信号星座点与二维空间中的PSK信号星座点的最小欧式距离相近时，由于三维空间中可容纳更多的星座点，因而poPSK能同时传递更多的信息，从而获得更高的数据传输速率。在第4部分的仿真实验中验证这一观点。

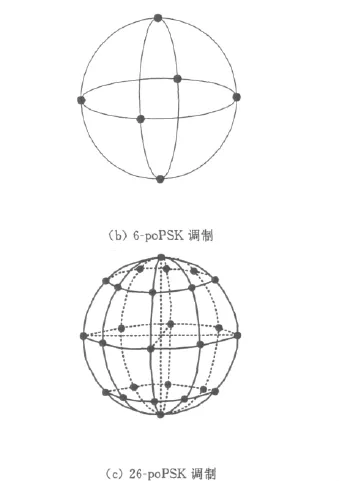
图3 三维poPSK调制信号星座图

4 三维调制信号误码率的计算与仿真

对于三维调制信号，星座点的坐标可以表示为（x0，y0，z0）。将信道噪声表示为（nx，ny，nz），它们都是均值为零，方差为σ2的加性高斯白噪声。经过信道传输后的接收信号可以表示为（x0＋nx，y0＋ny，z0＋nz）。可以看出，接收信号的均值为（x0，y0，z0），其联合概率密度分布可以表示为［3］

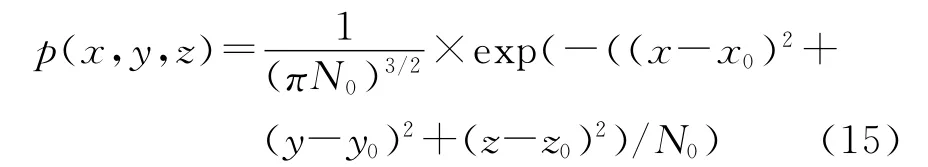
式中N0＝2σ2表示加性高斯白噪声的功率。

根据星座点的联合概率密度分布，接收端能够正确判决的概率可以表示为

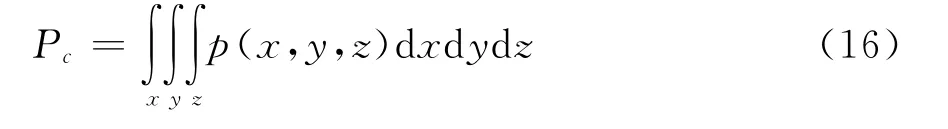
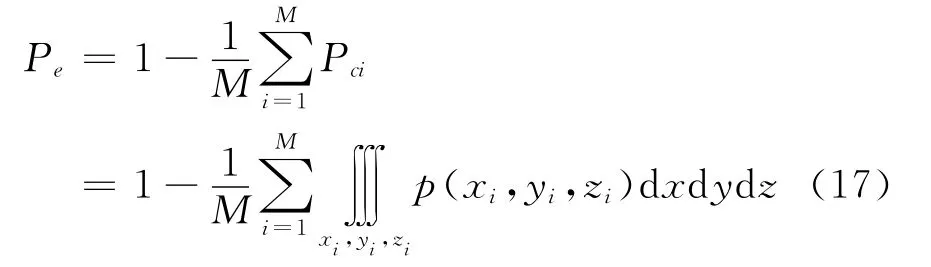
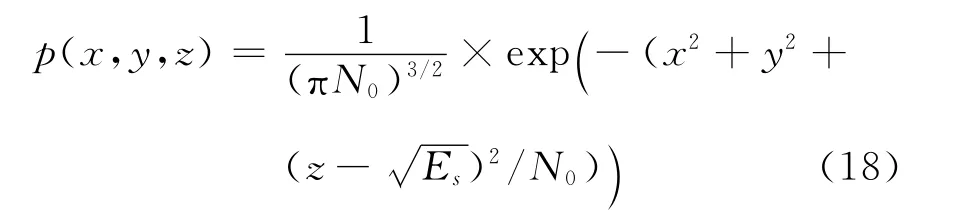
对x，y和z三个变量做三重积分，信号误码率的表达式为

式（19）一般不能简化为简单的计算形式，除了6poPSK调制的情况，需要采用数值分析。对于6poPSK调制，由于其6个星座点的坐标具有对称性，因此，其信号误码率可表示为

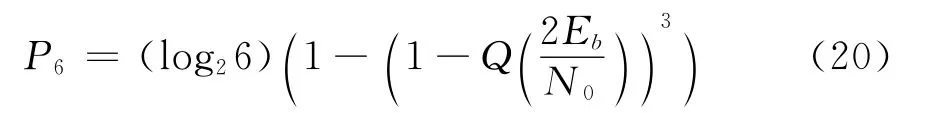
二维QPSK信号的4个星座点也具有对称性，其BER可以表示为

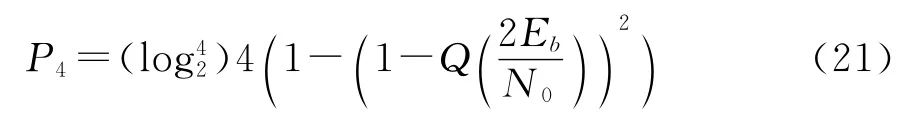
式中：

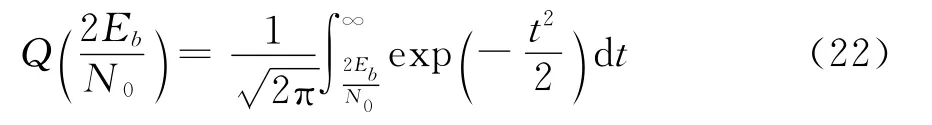
文献［3］中对图3中与4poPSK信号具有相同星座图的光通信调制信号误码率（BER）进行了仿真，我们将4poPSK、QPSK、6poPSK和6路双极化调制信号的BER进行了仿真对比，结果如图4所示。

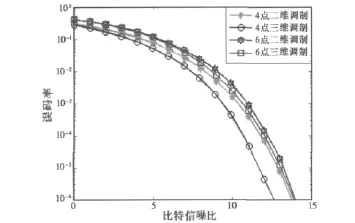
图4 几种调制信号误码率的对比

从图4中可以看出，在星座点数量为4的情况下，4poPSK比四相相移键控信号（QPSK）具有更低的误码率；在星座点数量为6的情况下，6poPSK比6路双极化调制信号具有更低的误码率。其原因是由于星座点数量相同时，分布在三维空间中的poPSK信号较二维空间中的PSK信号能具有更大的欧式距离，从而具有更低的误码率。图4中的仿真结果验证了理论分析结果，表明了本文所提出的极化与相位联合三维调制方法具有传输速率高和误码率低的特点。

5 结 论

本文提出了一种用矢量传感器将通信信号相位、极化幅度与极化俯仰角进行三维联合调制的方法，给出了极化与相位联合三维调制方法的调制与解调实现方式，画出了三维联合调制星座图和星座点分布，并对该调制方法的误码率做了仿真验证和对比。计算与仿真说明该方法具有传输速率高、误码率低的特点，在微波中继通信中有广阔的利用价值。

［1］MATALGAH M M，RADAYDEH R M.Hybrid frequency polarization SK modulation［J］.IEEE Journal of Light Wave Technology，2005，23：1152－1163.

［2］PORATH J E，AULIN T.Design of multidimensional signal constellations［J］.IEEE Proc Commun，2003，150（5）：317－323.

［3］KHABBAZIAN M，HOSSAIN J，ALOUINI M S，et al.Exact method for the error probability calculation of three dimensional signal constellations［J］.IEEE Trans Communications，2009，57（4）：922－925.

［4］NAZARATHY M，SIMONY E.Error probability performance of equi－energy combined transmission of differential phase，amplitude，and polarization［J］.IEEE Journal of Light Wave Technology，2007，25（1）：249－260

［5］BENEDETTO S，GAUDINO R，POGGIOLINI P.Direct decection of optical digital transmission based on polarization shift keying modulation［J］.IEEE Journal on Selected Areas In Communications，1995，13（3）：531－542.

［6］王被德.电磁波的极化及其应用［J］.电波科学学报，1999，14（3）：347－356.WANG Beide.Polarization of electromagnetic waveand its applications［J］.Chinese Journal of Radio Science，1999，14（3）：347－356.（in Chinese）

［7］NEHORAI A.Vector－sensor array processing for electro－magnetic source localization［J］.IEEE Trans Signal Processing，1994，42（2）：376－398

［8］BULL J F.Field Probe for Measuring Vector Components of an Electromagnetic Field：U S 300885［P］.1994－04－05.

［9］CHIU C Y，YAN J B，MURCH R D，et al.Design and implementation of a compact 6－port antenna［J］.IEEE Antennas Wireless Propagat Lett，2009，8：767－770.

［10］WONG K T，ZOLTOWSKI M D.Closed－form direction－finding with arbitrarily spaced electromagnetic vector－sensors at unknown locations［J］.IEEE Trans Antennas Propagat，2000，48（5）：671－681.

［11］黄家才，石要武，陶剑舞.基于双电磁矢量传感器的近场源多参数估计［J］.电波科学学报，2004，22（5）：848－854.HUANG Jiacai，SHI Yaowu，TAO Jianwu.Parameters estimation of near－field sources based on dual electromagnetic vector sensors［J］.Chinese Journal of Radio Science，2004，22（5）：848－854（in Chinese）

［12］王兰美，王洪洋，廖桂生.提高信号到达角估计精度的新方法［J］.电波科学学报，2007，20（1）：91－94 WANG Lanmei，WANG Hongyang，LIAO Guisheng，Novel method for estimation of the angles of arrival based on vector sensors［J］.Chinese Journal of Radio Science，2007，20（1）：91－94.（in Chinese）

［13］王兰美，廖桂生，王洪洋.矢量传感器增益校正与补偿［J］.电波科学学报，2005，20（5）：687－690.WANG Lanmei，LIAO Guisheng，WANG Hongyang.Calibration and remedy for vector－sensor［J］.Chinese Journal of Radio Science，2005，20（5）：687－690（in Chinese）

［14］伍裕江，聂在平.多天线系统中的多维极化分集性能分析［J］.电波科学学报，2007，22（3）：365－369.WU Yujiang，NIE Zaiping.Performance analysis of multi－polarization diversity in MIMO wireless communications［J］.Chinese Journal of Radio Science，2007，22（3）：365－369.（in Chinese）

［15］COMPTON R T.The triple antenna：an adaptive array with full polarization flexibility［J］.IEEE Trans Antennas Propagate，1981，29（6）：944－952.

［16］WEISS A J，FRIEDLANDER B.Maximum likelihood signal estimation for polarization sensitive arrays［J］.IEEE Trans on antenna and propagation，1993，41（7）：918－925.