复杂地形多测风塔综合地貌及风切变拟合修正的风资源评估方法研究

迟继峰，钟天宇，刘庆超，张伟

(1．中国华电集团公司，北京 100031;2．华电电力科学研究院，浙江 杭州 310030)

0 引言

评估风电场的风能资源状况，是开发风力发电项目最基础的工作。其中，风速概率分布参数是体现风能资源统计特性的最重要指标之一，也是在风电场规划设计和并网技术研究中的关键参数。

国内、外现有的风能资源评估方法主要有3种:基于气象站历史观测资料的评估方法，基于测风塔测风数据的评估方法，基于数值模拟的评估方法［1］。

数值模拟是目前较为常用的方法，主要借助基于各种数值模拟算法的计算机软件，并对该区域障碍物情况进行设置，通过某一点(测风塔某高度处)风资源数据，测算区域内各个高度风资源的分布情况，从而选择最优的地点建设风机。但由于粗糙度设置、软件误差及其他原因，风资源计算常存在一定误差，在复杂地形中该种情况更为明显。

因此，如何根据测风塔的实测数据，再考虑地形地貌的影响，确定该区域风切变系数，对于准确估算各风电机组轮毂高度处的风资源具有重要意义。

1 复杂地形多测风塔综合地貌及风切变拟合模型

1．1 山体坡度与风加速分析

风加速效应通常指在山地地形中，某高度平均风速比平地相应高度平均风速所增加的效应，一般在山顶的近地面最为明显。在隆升地形中，盛行风向与山脊脊线正交时，气流加速最大，倾斜时加速作用减弱，在山脊峰处达到最大。

隆升地形有不同形状，不同山体形状对加速效应的影响有明显不同。根据Taylor和Lee的“原始算法”，可以计算山顶不同高度处的加速比［2］:

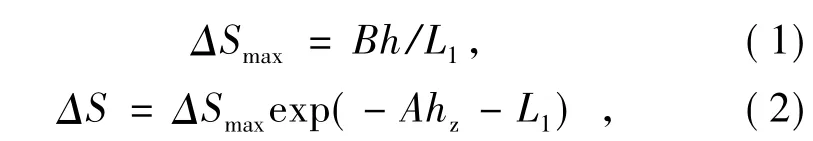
式中:ΔS为风加速比;A，B为经验常数，其数值见表1;h为山顶高度;L1为山顶到h/2高度处的水平距离;hz为海拔高度。

二维山体风加速效应如图1所示，二维连续山体风加速效应如图2所示。

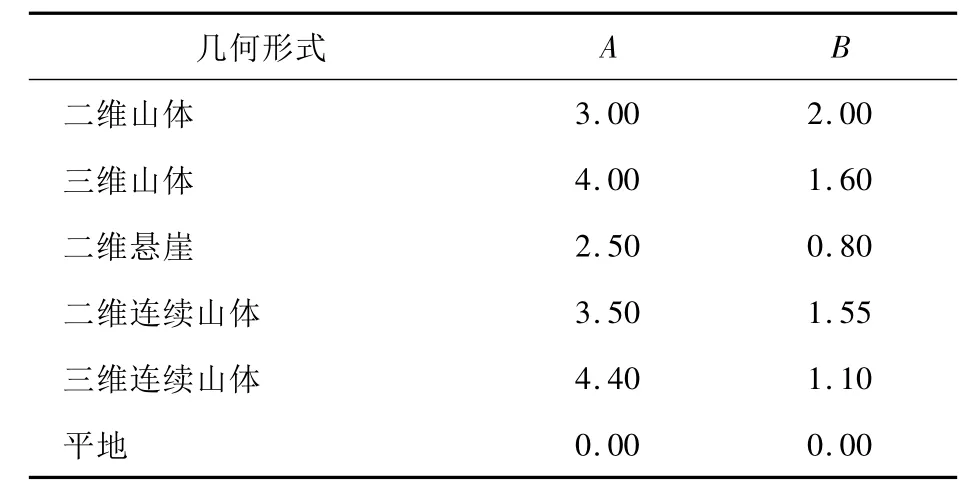
表1 不同地形下的A，B值

1．2 粗糙度与风速的关系

在近地层中，风速随高度的变化较为显著，造成风在近地层中垂直变化的原因有动力因素和热力因素。前者主要来源于地面的摩擦效应，即地面的粗糙度，后者主要表现为与近地层大气垂直稳定度的关系。当大气层结为中性时，湍流将完全依靠动力原因来发展，这时风速随高度变化服从普朗特经验公式［3］

式中:un和ui分别为高度在hn和hi处的风速;α为风切变指数。

1．3 风向水平偏差与地形、地貌的关系

风向水平偏差是指由于地形、地貌影响导致的风向水平偏转程度，主要是障碍物使风速、风向产生紊流，进而使风向产生偏差。紊流产生的主要原因有以下 2 种［4］:

(1)热紊流是由于热能交换(温度不同的物质会进行热交换)引起的，因此，受到地表温度和空气质量的影响。

(2)力紊流是受地貌学(用于描述地表状态)、地表粗糙度和地表障碍物的影响而形成的。

紊流强度随着地表粗糙度以及障碍物的增加而增加，随着高度的增加而减小;树木和障碍物(建筑物、围墙、栅栏等)可以给风减速并形成紊流，因此山区的风含有较多紊流。

1．4 拟合模型

由以上分析可知，复杂地形风速变化情况主要与山体坡度和形状、植被覆盖情况及风向的相关性较大，因此，复杂地形条件风切变计算应综合考虑多个测风塔风速玫瑰图、所在山体各个风向坡度、所在山体植被高度等影响因素。

当多个测风塔风速玫瑰图(x1)、测风塔所在山体各个风向坡度(x2)及测风塔所在山体植被高度(x3)与各个测风塔实测数据风切变系数(y)满足线性相关时，可采用三元线性回归方程模拟各个风机点的风切变系数。

式中:y 为风切变系数;a，b，c，d 为常数。

当各个影响因素x1，x2，x3与风切变系数y为非线性关系时，可采用BP神经网络模型或支持向量机模型模拟各个风机点的风切变系数［5］。计算过程如下:

(1)选取不同测风塔及风机点位所在位置各个参数数据;

(2)对数据进行归一化处理;

(3)运用BP神经网络或支持向量机模型对各个风机点的风切变系数进行模拟计算。

2 复杂地形多测风塔综合地貌及风切变拟合修正的风资源评估方法

根据以上分析，可以建立复杂地形条件下多测风塔综合地貌及风切变拟合修正的风资源评估模型，如图3所示。

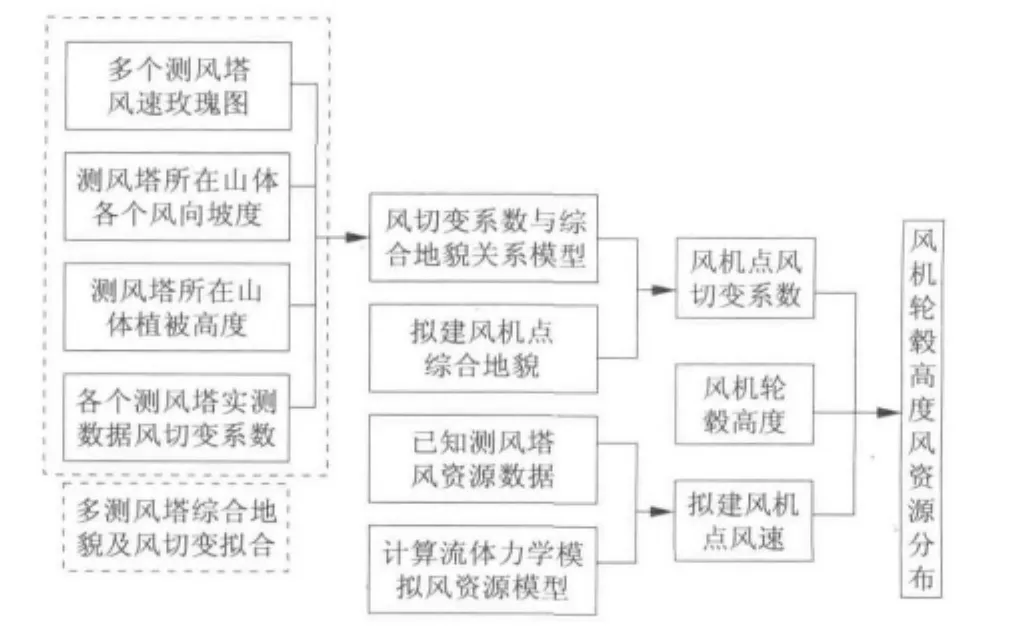
图3 复杂地形多测风塔综合地貌及风切变拟合修正的风资源评估模型

该模型主要计算过程如下:

(1)搜集拟建风场区域各个测风塔及风机点位综合地貌及风资源数据。

(2)根据测风塔风切变与综合地貌的相关性，运用复杂地形多测风塔综合地貌及风切变拟合模型对各个风机点位的风切变系数进行分析计算，根据具体情况可采用线性回归方程、BP神经网络或支持向量机进行模拟计算。

(3)根据已知测风塔固定高度风资源数据及其他数据，运用计算流体力学方法计算拟建风机点测风塔高度风速。

(4)运用式(3)计算风机轮毂高度处风资源的分布情况。

3 实例分析

以浙江沿海某风电场为例验证该模型的精确性，该风电场主要地貌为山地丘陵，高度一般为海拔100～400m。该区域共建设5座测风塔，各测风塔数据见表2。

表2 各个测风塔数据

根据以上数据可知，该风电场区域各测风塔风切变系数主要与粗糙度相关。以#1，#2，#3，#4测风塔为样本，粗糙度作为自变量，风切变系数作为因变量，运用数理统计方法中的线性回归理论，可得到风切变系数随粗糙度变化的方程

式中:x为粗糙度;y为风切变系数。

运用#5测风塔数据进行检验，根据粗糙度计算出的风切变系数为0．080 3，误差为1．49%，精度较高。

然后运用#4测风塔1月70m高度的风速对#5测风塔60m高度的风速进行模拟。

运用传统风资源计算方法:输入#4测风塔70m高度测风数据，运用软件直接推算60m高度的风速，其平均误差为 －4．28%，绝对平均误差为6．28%。

多测风塔综合地貌及风切变拟合修正的风资源评估模型:输入#4测风塔70m高度测风数据，运用软件推算70m高度处的风速，根据模拟的风切变系数，运用式(3)推算60m高度处的风速，其平均误差为－1．35%，绝对平均误差为2．35%，精度较高，如图4所示。

图4 各种计算方法与实测风速对比图

4 结论

(1)多测风塔综合地貌及风切变拟合修正的风资源评估模型，以计算流体力学理论对复杂地形风资源分布情况进行了模拟，总结出一套复杂地形风资源评估方法。运用该方法进行风资源分析，提高了评估的准确度及国内该方面技术研究及工程应用的理论水平和技术水平。

(2)该模型是针对目前设计人员在计算软件输入过程中无法完全准确模拟风电场区域地形、地貌等条件而提出的一种修正方法，实例证明该方法十分有效。

［1］宫靖远．风电场工程技术手册［M］．北京:机械工业出版社，2004．

［2］杨振斌，薛析，桑建国．复杂地形风能资源评估研究初探［J］．太阳能学报，2004，25(6):744 －749．

［3］李正良，孙毅，魏奇科，等．山地平均风加速效应数值模拟［J］．工程力学，2010，27(7):32 －37．

［4］陈严，张锦源，王楠，等．风力机风场模型的研究及紊流风场的Matlab数值模拟［J］．太阳能学报，2006，27(9):955－960．

［5］Yuan Chunhong，Xue Heng，Yang Zhenbin．A Numerical Modeling Study for Offshore Windspeed［J］．Acta Energiae Solaris Siniea，2004，25(6):740 －743．