轴向力作用下岩柱抗弯刚度的数值解

皮智鹏 胡和平 肖建清

(1．南华大学城市建设学院，湖南衡阳 421001; 2．安阳师范学院建筑工程学院，河南安阳 455000)

0 引言

一般材料的抗弯刚度都可以用四点弯曲试验得到，然而由于岩石的抗拉能力太弱，所以在很低的拉应力下试件即会破坏。为了解在具有较大地应力下矿柱或洞室中岩体抵抗弯矩的能力，需要十分复杂的力学试验仪器，这为工程及科研带来了一定难度。本文根据一般的材料力学和连续介质力学假定，分别以实验室中小体积岩石的和地下工程中使用的宏观岩体的本构关系为依据，使用MATLAB语言对有轴向力作用下岩柱截面进行计算机仿真，得到其不同轴向力作用下的弯矩曲率的变化情况，并用以分析轴向力对岩柱抗弯刚度及岩爆的影响。

1 岩石的本构关系

1．1 岩石受压时的应力应变曲线

岩石本构关系一般都是根据岩块的单轴或三轴试验得到的应力应变曲线，然后通过数理统计回归分析得到。不失一般性，在受压情况下，岩石的应力应变曲线可以分为五个阶段:分别为压密、弹性、屈服、软化和塑性流动阶段。基于此，本文参考文献［1］［2］，建立符合试验室小试件岩石物理特征的分段线性模型(见图1);考虑尺寸效应，参考文献［3］，建立符合洞室及矿柱岩体物理特征的尖角突变模型。

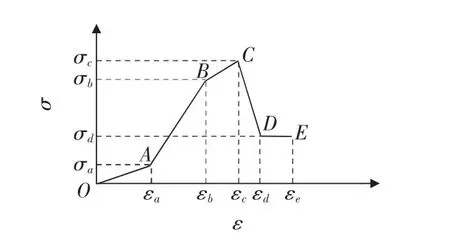
图1 分段线性模型

1．1．1 分段线性模型

OA段:

AB段:

BC段:

CD段:

DE段:

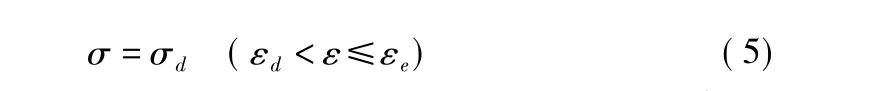
其中，(εa，σa)，(εb，σb)，(εc，σc)，(εd，σd)，(εe，σe)分别为岩石在压密、弹性、屈服、软化和塑性流动阶段末端的应变和应力值。

1．1．2 尖角突变模型

尖角突变模型见图2。

图2 尖角突变模型

弹性阶段:

塑性软化阶段:

塑性流动阶段:

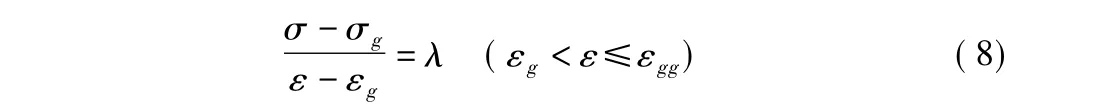
其中，σc，εc分别为峰值应力和应变;σg，εg分别为峰值后拐点处的应力和应变;Ec为岩石的压缩模量;λ为拐点g处的斜率绝对值，为岩石降模量。

1．2 岩石弯曲拉伸时的应力应变曲线

由于岩石材料的特殊性，一般无法直接测得其在受拉情况下的应力应变关系，而由巴西圆盘试验和三点、四点间接拉伸试验研究，岩石在受到拉应力时，开始时岩石的变形与荷载可认为是线性关系，随着荷载的增加，岩石突然被拉断，极限拉应变非常小(见图3)。综合考虑以上情况，其计算模型可以简化为:

其中，σt，εt分别为岩石受拉时的极限应力和极限应变;Et为岩石的拉伸模量，根据文献［4］，可取0．6 倍 ～0．8 倍 Ec。

2 不同轴向力下岩柱弯矩曲率关系的求解

2．1 岩柱横截面的几何相容方程

基于平截面假定，忽略岩石非均质影响，将岩柱截面沿弯曲方向分成n个条带，假定同一条带上各点的应变和应力均等于该条带中心点处的应变和应力。由于岩石受拉应力应变关系和受压应力应变关系的差异，岩柱截面在压弯时的中性轴将不在其截面的中心线处，不妨设截面中心线处的应变为ε0，则第i个条带处岩石的应变为:

其中，ε0为截面中心线处的应变;Zi为每个条带中心到截面中心的距离;φ为截面的曲率。

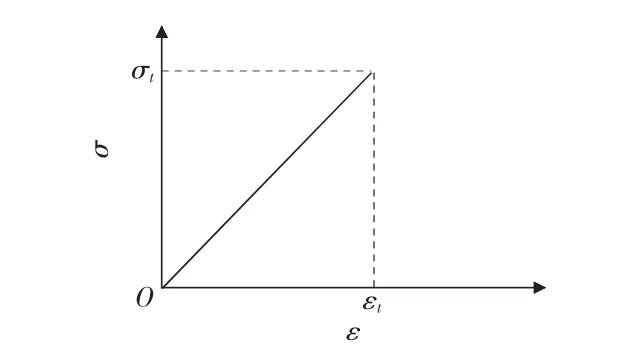
图3 岩石在弯曲拉伸时的本构模型

2．2 岩柱横截面的物理方程

岩柱截面上每个条带的应变值为一个关于ε0的线性函数，代入岩石的本构关系中，可以得到岩柱截面处每一个条形的应力函数，它同样也是关于ε0的函数，具有非线性特征。在计算中可规定截面处应力以受压为正，受拉为负。

本构方程为:

其中，f为岩石应力与应变的映射关系，具体查看上文中的岩石的两种受压本构模型和受拉本构模型。

2．3 岩柱横截面的平衡方程

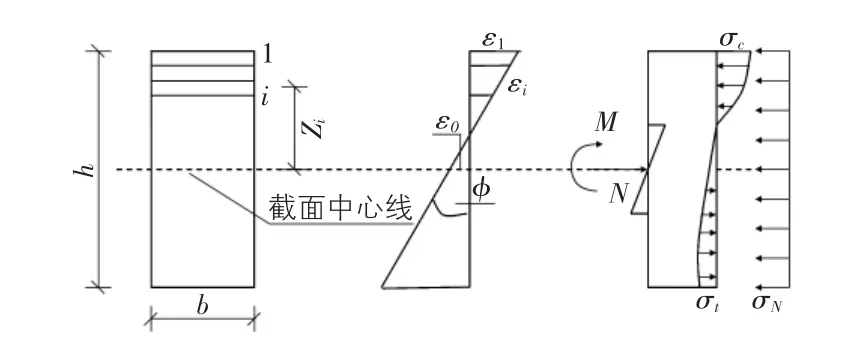
图4 轴向力作用下岩柱横截面的条带分析模型

由图4建立静力平衡方程:

解非线性函数方程组(12)，可得到在固定φ值的截面处使得内力为N的 ε0值，然后把 ε0和固定的 φ代入第二个方程组(13)，得到该截面的弯矩值，改变φ值，就可得到在定轴力N下不同曲率下的截面弯矩大小，即M—φ曲线。

3 算法流程

本文利用MATLAB编程，运用多M文件嵌套技术，通过更换本构方程(11)，用试位法(method of false position)［5］求解平衡方程组(12)，用求得的σi代入方程(13)得到岩柱截面弯矩值，所求弯矩曲率曲线的斜率值即岩柱在不同轴向力下的抗弯刚度。

4 算例

分段线性模型:

尖角突变模型:

Ec=40 GPa，σc=60 MPa，εg=0．002 0，σg=45 MPa，εgg=0．003 0。

岩石抗拉强度取抗压强度的10%，受拉模型:

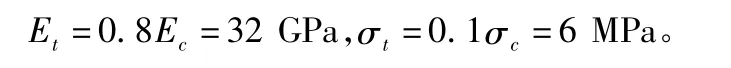
岩柱横截面尺寸为50 mm×300 mm，截面初始曲率为2×10－5m－1，每次递增一倍，至0．01 m－1结束。轴力从10 kN 依次递增到50 kN。计算结果见图5，图6。

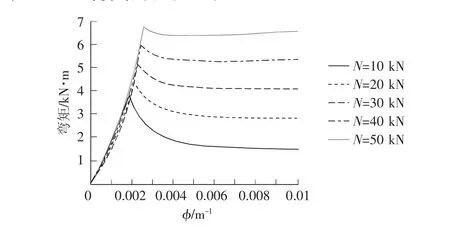
图5 由分段线性模型计算得到的M—φ曲线

图6 由尖角突变模型计算得到的M—φ曲线

5 结语

1)由尖角突变模型计算得到的岩柱截面M—φ曲线在前段呈线性变化，其曲线斜率即岩柱截面的抗弯刚度EI，与EcI值十分接近。由分段线性模型计算得到的M—φ曲线在前段却已有非线性特征，这主要是由岩石的压密和屈服段的计算弹性模量与弹性段的弹性模量不同引起的，其平均斜率值与EcABI接近，EcAB为岩石在弹性段的弹性模量。2)随着轴向力的增加，岩柱在线性段能抵抗的极限弯矩随之升高，这是由于这里的极限弯矩由拉应变控制，岩石能承受的拉应变非常小，而随着轴向力的增加，岩柱微段有一个随着轴向力增加的相对较大的压应变区，中和弯矩引起的拉应变，使得岩柱能承受的极限弯矩有所提高，进入软化区的界限曲率也在随之增大。这在地下工程中有着积极的意义，若把采矿中矿柱受到的地应力简化为轴向力，可以推知，随着地应力的增加，矿柱能抵抗的极限弯矩逐渐增大。3)岩柱一侧曲率超过界限值时，弯矩曲率曲线发生突变，岩柱进入能量耗散阶段，这在两个物理模型得到了统一结果。这时岩柱截面发生软化，岩柱的抗弯刚度为负值，到达岩体的扩容阶段时，岩柱的抗弯刚度基本为零，理论上岩爆可能发生在岩体能量开始耗散的阶段。若假设矿柱在某一截面发生岩爆，设截面厚度为1，根据曲率和转角关系，则上面的计算结果也可看成是岩柱某截面(或岩爆截面)的M—θ关系图，一般认为岩爆发生是岩石存储的弹性应变能突然释放发生的动力失稳现象［6，7］，计算结果表明随轴向力增加，其在弹性区储存的弯曲应变能也随之增加［8］，推之，随地应力增加岩爆中释放的弯曲应变能愈大。

［1] 戴 俊．岩石动力性特性与爆破理论［M］．北京:冶金工业出版社，2002:14-16．

［2] 解廷堃，李二利，刘如成．炭质页岩常规三轴试验和本构方程的研究［J］．露天采矿技术，2008(6):7-12．

［3] 潘一山，章梦涛，李国臻．洞室岩爆的尖角突变模型［J］．应用数学与力学，1994，15(10):893-900．

［4] 杨 同，王宝学，高 谦，等．岩石弯曲拉伸试验研究［J］．勘察科学技术，2004(6):3-5．

［5] John H Mathews，Kurtis D Fink．数值方法(MATLAB 版)［M］．北京:电子工业出版社，2011:45-48．

［6] 唐礼忠，潘长良，王问星．用于分析岩爆倾向性的剩余能量指数［J］．中南工业大学学报，2002，33(2):129-132．

［7] 李庶林，唐海燕．岩爆倾向性的弹性应变能指标法［J］．矿业研究与开发，2005，25(5):16-18．

［8] James M Gere．Mechanics of Materials［M］．Beijing:China Machine Press，2009:656-658．

［9] Timoshenko S P，Gere J M．弹性稳定理论［M］．北京:科学出版社，1965:180-185．

［10] 李江腾．初始几何缺陷对超高矿柱稳定性的影响［J］．岩石力学与工程学报，2005，24(22):4185-4189．