板形环受热变形有限元分析及理论计算研究(续)

刘文田， 陈林， 冯少鹏， 程瑞敏， 常华

(苏州有色金属研究院有限公司，江苏 苏州，215026)

表2 各温度下安装孔的变形

孔编号1234温度5155.255.453直径60.020660.018860.021160.0148

孔编号1234温度6365.666.163.2直径60.038560.037260.0460.0385

孔编号1234温度71.271.873.172直径60.045160.045260.046660.0455

从表2中数据可以得知，各安装孔的直径随着温度的升高而增加，3号安装孔在图2中所示状态离带材最近，因此温度也最高，热膨胀量最大，直径为60.0466mm。

3 板形环整体热变形理论计算

1)由热应力所产生的热变形

根据应力与位移的关系[2]，有

(5)

其中E—弹性模量；μ—泊松比；α—线膨胀系数；T—孔形零件内部温度；σr、σθ、σz—孔型零件径向、环向、轴向的应力分量；uruz—孔型零件在径向和轴向的位移分量。

由应力分量表示的平衡微分方程为

(6)

式中:τzr—重力在轴向的剪应力分量，fr、fz—径向和轴向的体积力分量。

当零件温度变化仅为r的函数且不考虑零件重力和残余应力的情况下，平衡微分方程可以简化为

(7)

(8)

将式(5)代入式(8)，有

(9)

式(9)中：εz—零件在轴向的应变分量。

将式(5)代入式(7)，有

(10)

假设零件轴向温度场为稳态温度场，由式(9)可知

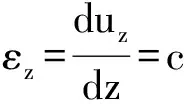
(11)

将式(10)进行变形可得

(12)

将式(12)两边对r进行两次积分可得

(13)

式中A、B为定积分常数。

将式(11)和式(13)代入式(5)，则得到

(14)

(15)

因为不考虑零件加工的残余应力和外力作用，所以在r=r1,r2处径向应力为零。即可以求得定积分常数A、B

(16)

(17)

因为不考虑零件重力的因素，所以轴向应力的平衡式为

(18)

将式(15)中的σ2代入式(18)中，则有

(19)

由式(16)(17)(19)得到热应力引起的变形量为

(20)

如果零件工作时内壁的温度为T1，外壁的温度为T2，轴向的传热可以不计，温度仅沿径向发生变化，其导热微分方程

(21)

将式(21)代入式(20)，可以得出由于热应力而产生的变形量度为

(22)

将材料参数代入上式，可得

ur=25.07143×10-6×

取r=0.14，

可求得

ur=9.8994×10-5m=0.098994mm

2)自由膨胀变形量

由于温度只在径向发生变化，而零件几何尺寸的变化与半径和温度有关，那么可以得到零件受热后几何尺寸变化与半径的几何关系。

通过下面的计算可以得到零件内部任何部分的热膨胀量

(23)

如果零件初始温度为T0，那么

(24)

将式(24)代入式(23)，则可以得到由于热膨胀引起的变形量

(25)

将材料参数代入上式，可求得

△r=1.0582×10-4m=0.10582mm

3)孔型零件在稳态非均匀温度场中的热变形量

孔型零件在稳态非均匀温度场中的热变形量应该是由于热应力引起的变形量和自由膨胀引起的变形量之和

△r=ur+△r

(26)

可求得

△r=0.20481mm

由此可得，板型环外径变化值为

△D=0.409mm

理论计算得到的板形环整体热变形量为0.409mm，而有限元仿真得到的板形环的热膨胀量为0.38mm，相差不大，说明有限元仿真得到的结果与理论计算得到的结果基本吻合。

4 结束语

应用有限元数值计算方法，以有限元软件为工具，对压磁式板形测量仪中的板形环在工作状态下受热产生的热变形进行了分析，得到了板形环在热平衡状态下的温度场分布及总体热变形量，板形环的总体热变形量与理论计算所得结果基本吻合；并得到了各安装孔的热变形量，因此在板形测量仪的设计过程中可以给出相应的配合尺寸补偿值，保证在工作温度变化后仍具有优良的配合，对压磁式板形测量仪的设计及安装都具有重要的指导意义。

[1] 马泳涛,陈五一.基于有限元法的圆筒零件热变形研究 [J].矿山机械,2006,36(7):35-36.

[2] 杨世铭,陶文铨.传热学(第四版)[M].北京：高等教育出版社, 2006.

[3] 胡鹏浩.非均匀温度场中机械零部件热变形理论及应用研究 [M].合肥：合肥工业大学出版社,2001.

[4] 罗哉，费业泰，苗恩铭. 稳态非均匀温度场中孔型零件变形研究 [J].应用科学学报,2005,23(4):424-427.