地区电网动态等值模型和等值方法的改进

杨白洁，袁铁江，晁勤，常喜强，衣海东

（1.新疆大学电气工程学院，新疆乌鲁木齐830047；2.新疆电力公司，新疆乌鲁木齐830002；3.新疆科林思德新能源有限公司，新疆乌鲁木齐830011）

近年来，互联电力系统的出现使电力系统的规划和不同运行方式下的计算复杂性增大。为此需要有效的等值方法对地区电网进行简化，把不需要详细分析或参数不详细的部分等值，在缩小系统规模的同时，保证研究系统等值后进行分析、控制的精度。文献[1-2]介绍了当前等值研究的各种方法和主要思路。

目前，外部系统的简化方法一般可以归结为两类：静态等值法和动态等值法。静态等值法主要是针对潮流计算，而动态等值法则考虑电网的暂态行为。文献[3]提出通过一台等值机及端口数有关的固定接线方式的简单网络来做静态等值，对数-相图和极坐标2种形式的目标函数，利用最小二乘法拟合目标参数，应用模矢搜索法获得一组拟合效果最佳的等值发电机参数。对等值前、后系统模拟故障，比较发电机在模拟时间段内的摇摆曲线逼近程度对等值参数进行微调，但是该方法的等值结果适合BPA机电暂态仿真工具，在电磁暂态软件中没作相关分析。文献[4]对等值过程中可能出现的误差进行分类和分析，揭示了多端等值法的2类非线性误差产生的机理，提出了有效的解决方法，但是没有提出系统故障时对外界的影响减小的机理。文献[5]利用小生境免疫算法对等值模型进行参数辨识，该方法估计精度高，鲁棒性强，能避免早热问题，使用性强，但是算法较复杂。等值可以提高计算速度，但也给电网带来了计算精度上的误差。国内外对电网等值情况均有相关的研究成果[6-12]，但是如何保证静态和动态下都能使外网对内网的影响减小到最小尚需研究。

本文就等值过程外部对内部网络的影响问题进行了讨论，分析了等值过程中产生的误差，提出改进措施，保证了等值前后静态边界潮流和动态情况下外网对内网注入的功率不变。最后将该方案应用到PSASP软件中的8机36节点系统，以此验证该方案的正确性和实用性。

1 现代动态等值问题与结构模型

对于大型电力系统采用系统等值不仅要保留系统的主要特征，还要减少系统状态变量，降低系统方程的维数，减少计算的复杂性和对计算机内存、CPU时间的消耗。一般以下情况需要动态等值：1）大规模电力系统的离线暂态（大扰动）稳定分析；2）大规模电力系统的离线动态（小扰动）稳定分析；3）大规模电力系统的在线动态安全分析。动态等值方法有3种：1）基于相关性概念的同调等值法；2）基于线性化系统状态方程的模式等值法；3）基于系统动态响应（或测量）来于在估计和辨识外部系统及其等值参数的方法[1]。

电力系统一阶数学模型可以表示为[1]

式中，X∈Rn是降阶前系统的所有状态量；V是节点电压向量；I是节点注入电流向量。系统降阶简化后的数学模型如下：

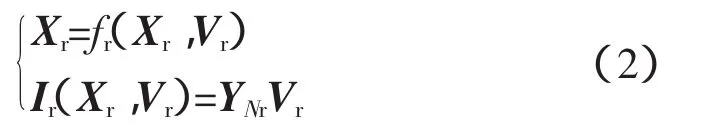
式中，Ir、Vr分别是降阶系统的节点注入电流向量和电压向量；X∈Rnr是降阶后系统的状态量，其数目远小于降阶前原型系统状态量，即nr＜n。降阶系统的状态量和非线性微分方程数目远小于原型系统，这使得等值系统中的动态元件数目大大减少，极大降低了等值系统的状态量和微分方程数目，提高计算速度。

目前，主要提出了3种等值结构模型[2]。1）实际联络线模型；2）等值联络线模型；3）带有缓冲区的多机模型。

2 外部网络的等值

当用一台恒定的电势模拟电机来等值时，其等值惯性常数为[3]

按各发电机的惯性加权平均，等值机的等值电势角及恒定电势值为

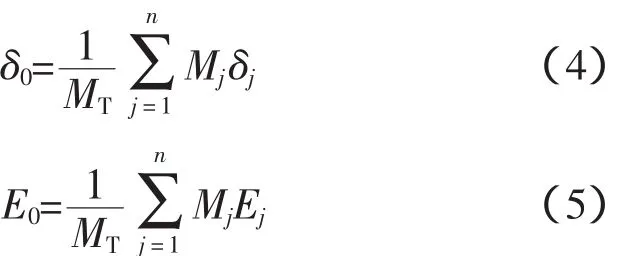
式中，Mj、δj、Ej分别为各发电机的惯性常数、电势角及恒定电势。通过以上各式的计算，可以求出系统的惯性中心；然后将该惯性中心的电势通过一定的网络连接，以满足系统的电气等值关系，在此采用包括惯性中心等值电势在内的等值网络。

3 等值误差分析及改进措施

3.1 误差来源及分类

通过分析可知，上述所采用的等值方法其等值误差来源主要有以下几点：

1）等值时假定外网节点注入功率SE不变，但当电力系统内网运行状态发生变化时，状态量[VBVE]是变化的，即电网的运行方式对电网的等值有影响[4]。

2）在等值过程中把发电机群等值为功率恒定的发电机，即为PQ节点，而实际电力系统的外网中有PV节点、带有调速器的发电机节点以及并联对地支路等，等值中由于将这些因素忽略而导致非线性误差。

3）等值前后内网和外网的静态潮流计算要一致，实际仿真计算中静态潮流计算往往有误差。

4）等值机的暂态电抗、次暂态电抗、负序电抗及转动惯量对等值模型均有影响。

5）负荷模型对电网的等值也有一定的影响。当负荷接在变压器高、中、低侧时对电网等值短路计算的影响都是不同的。负荷选择“悬挂点”及负荷动态特性及对系统的影响也对计算结果产生误差。

6）零序网络的不同也对单相短路电流计算结果产生误差。

3.2 等值简化模型的优化

一般不需要对外部系统深入研究，或者在没有掌握外部系统的内部参数，如节点类型、负荷情况及并联对地支路等情况下，可以采用简便方法进行改进[5]。

通过上述分析可知，等值产生的误差主要来自5个方面，归结为发电机的电抗、网络参数、负荷模型及参数3个方面的影响，针对误差产生来源对等值采取如下改进措施：在内部系统与外部系统的边界线上附加母线，在母线上悬挂等值调节功率负荷和接地电阻，等值系统改进模型如图1所示。

图1 等值系统改进模型Fig.1 Improved equivalent system model

等值过程中应注意以下几点：

1）在等值时，要注意搭建统一的计算网架，保持统一的计算参数，以保证电网等值前后边界潮流保持不变。

2）正确设置等值发电机的电抗，以保证等值前后暂态计算结果误差较小。

3）在等值的边界线上附加母线，母线上接等值调节功率负荷，使电力系统运行状态变化时，负荷特性影响不变。

4）在附加母线上接接地电抗器，接地电抗器的参数可以通过外网边界短路实验得出，以保证网络动态特性不变。减少不对称故障，对计算结果产生影响。

4 算例

4.1 系统结构

本文采用的仿真模型是PSASP中的8机36节点系统，系统结构如图2所示，以19、16节点作为边界点，将原系统划分为1、2两部分，1为研究系统，2为外部系统。将BUS7、BUS8母线侧的发电机组等值为平衡机，其等值系统内部的负荷转移到等值机母线上，发电机之间的联络线转换成接地阻抗。

图2 8机36节点母线系统Fig.28 machine 36 node bus system

4.2 等值前后仿真结果比较

对其中待简化的子系统的参数采用加权平均法聚合，所有发电机以暂态电抗后恒定电势模拟，所有负荷以恒定阻抗模拟。根据上述方法得出等值发电机群和等值机参数，列于表1和表2，其中单位均为标幺值。

表1 等值发电机群和等值机参数Tab.1 Equivalent generators and their parameters pu

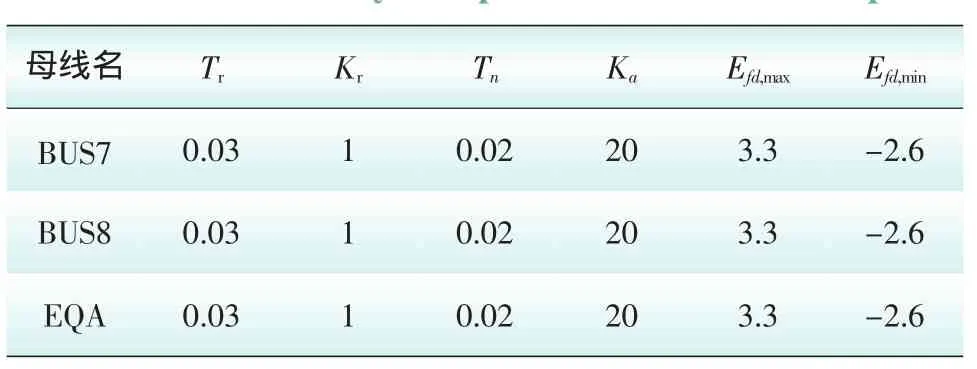
表2 等值发电机群和等值机励磁系统参数Tab.2 Equivalent generators and their excitation system parameter pu

对系统进行静态潮流计算，其等值前后边界潮流结果分别如图3、图4所示，图中数值单位采用标幺值。

图3 等值前边界潮流Fig.3 Boundary power flow before equivalent

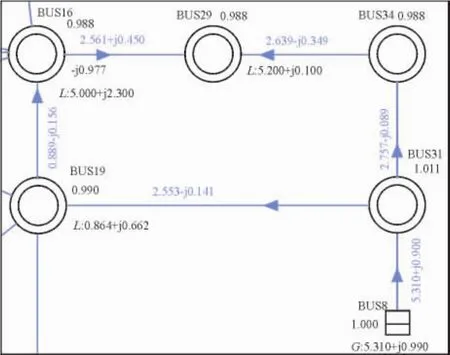
图4 等值后边界潮流Fig.4 Boundary power flow after equivalent

对网络等值前后进行动态仿真，其中在内部系统BUS9、BUS22之间支路上设置三相短路故障，故障时间段为0～0.12 s，仿真得出等值前后网络的保留发电机功角波动曲线如图5所示。

图5 等值前后网络的保留发电机功角波动曲线Fig.5 Network reserved generators power-angle wave curves before and after equivalent

4.3 等值改进措施及仿真结果

在此采取简便方法对8机36节点网架等值进行改进，即在边界加入调节功率的负荷和合适的接地阻抗，其等值边界调节功率及接地阻抗参数列于表3和表4，表中数值单位为标幺值。

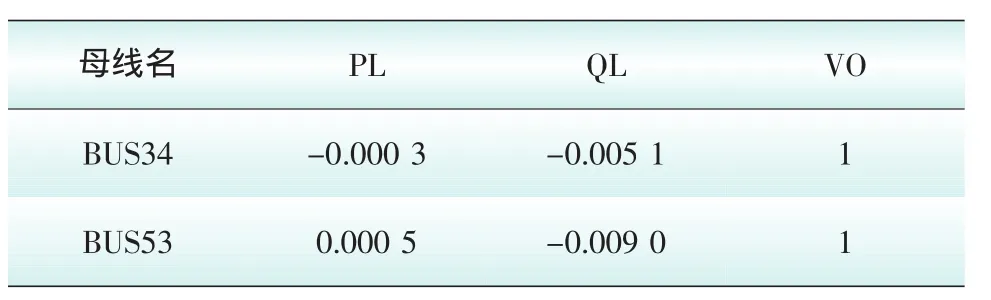
表3 等值电网边界调节功率负荷数据Tab.3 Equivalent power network boundary adjusting power loads data

等值系统改进后边界潮流结果如图6所示。

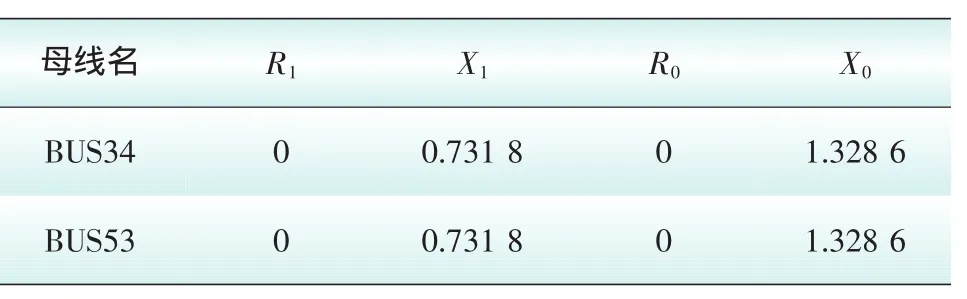
表4 等值电网边界接地阻抗数据Tab.4 Equivalent network boundary grounding impedances data

图6 等值系统改进后边界潮流Fig.6 Improved equivalent system boundary power flow

对于动态影响下的分析仍是在内部系统BUS9、BUS22之间支路上设置三相短路，时间段同上。由此仿真得出等值前和等值改进后网络的保留发电机功角波动曲线，如图7所示。

4.4 仿真结果分析

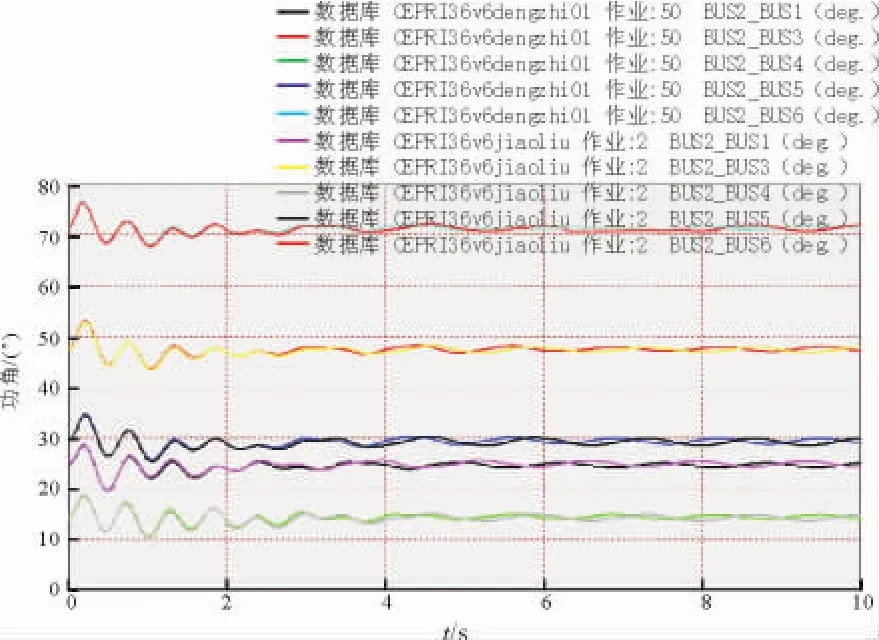
图7 等值前和改进后网络保留发电机功角波动Fig.7 Network reserves generators power-angle wave curves before and improved equivalent

根据图3、图4和图5可知，静态潮流下，等值前、等值后和等值改进后的边界母线电压和传输线路数据如表5和表6所示。

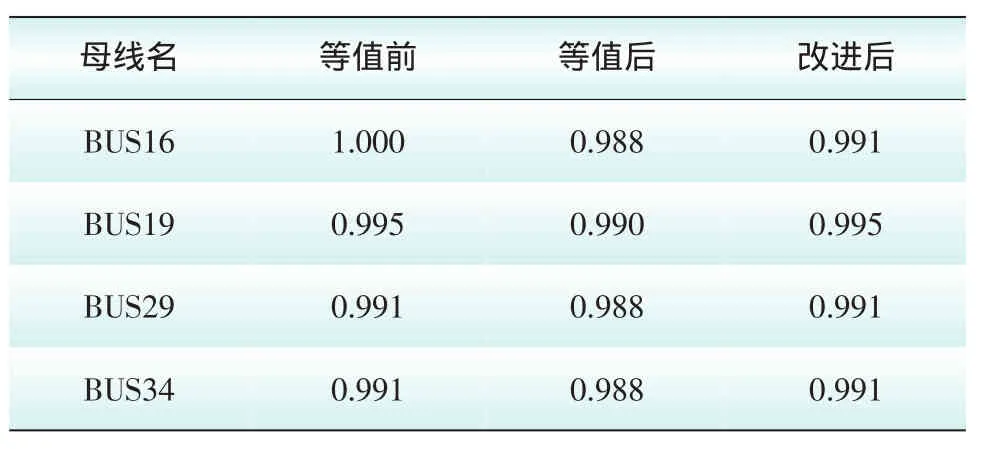
表5 系统等值前后和改进后母线电压Tab.5 Buses voltage data of after and before equivalent and after improved network pu

表6 等值前后和改进后边界线路传输功率Tab.6 Transmission lines power data after and before equivalent and after improved network pu

由表5和表6可知，等值前后初始边界潮流有功最大误差为0.124 pu，无功最大误差为0.024 pu，各边界节点电压幅值最大误差为0.012 pu；改进后的仿真结果误差减少了，其边界有功及无功潮流误差为0，各边界节点电压幅值最大误差为0.009 pu，节点角度误差为0。静态等值结果满足精度要求。

由图5可知，系统动态仿真过程，等值前后的保留发电机功角波动曲线误差为3%～5%，外部系统等值后对内部系统的影响有所改变，计算精度下降。由图7可以看出，等值改进后其网络中保留的发电机功角波动曲线误差较没有改进前仿真结果误差减少，误差降至1%～3%。等值改进后不仅使等值前后初始边界潮流一致，而且保证了在动态运行状态下等值系统对内部系统的影响几乎不变。

分析等值改进后，精度有所提高的主要由于将外部网络等值为包含代表其惯性的等值机，等值机可以大大简化网络结构，提高计算速度，同时保留了等值网络的主要参数结构。考虑了系统的开路和短路条件，在边界加入合适的调节功率负荷和接地阻抗，其作用是保证简化后的等值网络向内部网络注入的功率不变，同时，保留了边界短路电流特性。这是保证稳态下的等值边界条件和稳定计算过程中的暂态特性不变的关键因素。

5 结论

本文通过对系统等值、改进和实例仿真过程进行分析可得出以下几点结论：

1）采用静态等值法，并结合多端等值法的思路，不仅考虑了稳态运行方式下的边界条件，同时也对暂态过程中影响等值精度的因素进行了详细的分析，适合应用在潮流和暂态稳态计算下的等值，对于分析大型电力系统有较好的应用价值，方法简单易行，易于实现。

2）对发电机、励磁系统和调速系统等参数进行聚合，将等值系统内部的等值机群等值为一台EQA机，相应的负荷转移到等值机的母线上。该方法数学推导方便，计算过程简单，并且由于保留了原系统的动态特性，保证了等值系统对内部系统的影响不变，提高了计算精度。

3）采用中国电科院研发的PSASP仿真软件进行的仿真，由于该软件是目前电力行业普遍采用的软件，在此软件下验证得到的结果可用性较高。通过将改进的等值方法应用到仿真系统中进行验证，结果表明本文提出的动态等值方法是有效可行的，精度满足要求。

[1]倪以信．动态电力系统理论和分析[M].北京：清华大学出版社,2008.

[2]周海强，鞠平，杨辉，等．电力系统动态等值建模研究述评[J]．江苏电机工程，2008,27（5）：10-13．ZHOU Hai-qiang，JU Ping，YANG Hui，et al．A review of development in dynamic equivalent technologies for power system modeling[J]．Jiangsu Electrical Engineering，2008,27（5）：10-13(in Chinese)．

[3]杨琴，管森．基于大电网实时仿真中的动态等值[C]//中国高等学校电力系统及其自动化专业第二十二届学术年会，南京，2006．

[4]孙奇珍，蔡泽祥，朱林，等．互联电网的多端等值方法及其误差分析[J]．电网技术，2008,32（23）：67-71．SUN Qi-zhen，CAI Ze-xiang，ZHU Lin，et al．Multiterminal equivalence method of interconnected power system and improvement based on its error analysis[J]．PowerSystemTechnology，2008,32（23）：67-71(inChinese)．

[5]李晓辉，罗敏，刘丽霞，等．动态等值新方法及其在天津电网中的应用[J]．电力系统保护与控制，2010,38（3）：61-66．LI Xiao-hui，LUO Min，LIU Li-xia，et al．A new dynamic equivalence method and its application in Tianjin grid[J]．Power System Protection and Control，2010,38（3）：61-66(in Chinese)．

[6]刘志文，刘明波．基于支路等值注入功率模型的外部网络等值修正方法[J]．电力系统保护与控制，2010,38（21）：219-226．LIU Zhi-wen，LIU Ming-bo．A corrected external equivalent approach using branch equivalent injection power model[J].Power System Protection and Control，2010,38（21）：219-226(in Chinese)．

[7]孙素琴，蒋周士，周海强，等．电力系统动态等值中原动机调速系统聚合的研究[J]．电力系统保护与控制，2010,38（12）：24-34．SUN Su-qin，JIANG Zhou-shi,ZHOU Hai-qiang，et al．Aggregation of turbine and governing system for dynamic equivalents of power systems[J].Power System Protection and Control，2010,38（12）：24-34(in Chinese)．

[8]OURARI M L，DESSAINT L A，DOE V Q．Dynamic equivalent modeling of large power systems using structure preservation technique[J]．IEEE，2006,21（3）：1284-1295．

[9]OURARI M L，DESSAINT L A，DOE V Q．Generating units aggregation for dynamic equivalent of large power systems[J]．IEEE，2004,2（10）：1535-1541．

[10]JU P，ZHOU X Y．Dynamic equivalents of distribution systems for voltage stability studies[J]．IEEE,2007：22（2）：648-657．

[11]LO K L，QI Z Z，URQUHART B．Dynamic equivalents of powerstationsforoptimalcontrolofpowersystemsecurity[J]．IEEE，1993,2：456-461．

[12]NOJIRIK,SUZAKIST.Modelreduceddynamic equivalent model for analog type power system simulator[J].IEEE Trans on Power Systems,1997,12（4）:1518-1523．