基于膨胀力试验数据的膨胀土膨胀应变模型

贾景超，宋日英，黄志全

(华北水利水电学院资源与环境学院，河南郑州 450011)

膨胀土吸水膨胀给建于膨胀土地区的铁路线带来很大问题，南方几条主要铁路干线经过的膨胀土地区，路基拱起、基床翻浆冒泥、边坡滑塌等病害都十分普遍［1］。仅据襄渝线施工决算统计，由于膨胀土在施工期间造成的破坏，使路基造价大幅增加，实际投资约为设计造价的三倍［2］。

膨胀力与膨胀应变是反映膨胀土膨胀潜势的两个重要指标。膨胀应变试验通常是在固结仪中进行，因此膨胀应变一般是指试样的竖向膨胀量与试样初始厚度之比。试验时，将制样条件相同的试样分别装入固结仪中，施加小于膨胀力的不同荷载，加水使其膨胀至稳定，最终可得膨胀应变与外加荷载之间的关系。膨胀力是指在试样体积保持不变的条件下，试样吸水后产生膨胀变形而对约束产生的作用力，所以，测定膨胀力的关键是要保持试样的体积不变。在通常确定膨胀力的方法中，如膨胀加压法、恒体积法、分级加荷膨胀法和平衡加压法［2-3］，只有恒体积法是严格意义的保持体积不变。

恒体积法采用容器对试件进行约束，使试件不发生膨胀和压缩，试验开始后容器所受的力即为膨胀力。采用此方法要求容器的刚度要足够大，以防产生变形。此方法与膨胀力的定义最接近，且比较符合工程实际，因为在构筑物不容许地基发生变形的前提下，构筑物所受膨胀力即为恒体积情况下的膨胀力。

分级加荷膨胀法是根据膨胀应变确定膨胀力的方法，即在同样条件下制备多个试样，分别施加不同的恒定荷载，测得各试样在浸水后的膨胀应变。根据试验点绘制应变与荷载的关系线，如图1所示，图中使应变为零的压力即为膨胀力。此方法得到的膨胀力与恒体积方法所得结果较为接近［3］。

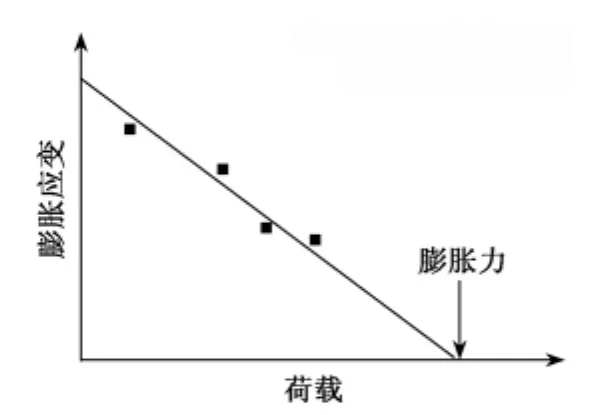
图1 分级加荷膨胀法

然而，以往的研究并未涉及如何根据膨胀力确定膨胀应变，所以多数情况下膨胀应变与膨胀力需通过各自的试验测定。本文通过分析膨胀变形的机理，得到膨胀变形与膨胀力的联系，进而建立了利用膨胀力试验结果确定膨胀应变的模型。

1 膨胀变形及膨胀力产生机理

膨胀土中亲水性矿物——蒙脱石吸水之后的体积膨胀，是导致膨胀土产生膨胀的根本原因。蒙脱石颗粒是由矿物晶层叠加而成，水分子进入到晶层之间使得晶层间距增大，从而使蒙脱石颗粒体积增大。随着晶层间距的增大，晶层之间的膨胀力将会减小。

膨胀土压实后土体中尚存在孔隙，遇水之后，膨胀土中的蒙脱石颗粒吸水致使自身体积增大，将首先充填周围的孔隙。如果保持土体体积不变(如膨胀力试验)，当蒙脱石颗粒将孔隙填充之后，将会受到周围颗粒的限制而不能再膨胀，被限制颗粒由此产生的膨胀力将会向周围颗粒传递，最终产生宏观膨胀力。膨胀力产生机理如图2(a)所示。

在膨胀变形试验中，蒙脱石颗粒吸水膨胀并将颗粒间的孔隙全部填充后，将会受到周围颗粒的限制从而产生膨胀力，如果由此产生的宏观膨胀力大于外加荷载，晶层间距将会继续增大，并导致膨胀变形的产生。而晶层间距的增大将使得晶层之间的膨胀力降低，当间距增大到一定程度，蒙脱石产生的宏观膨胀力将会与外荷载达到平衡，此时膨胀变形结束。膨胀变形产生机理如图2(b)所示。

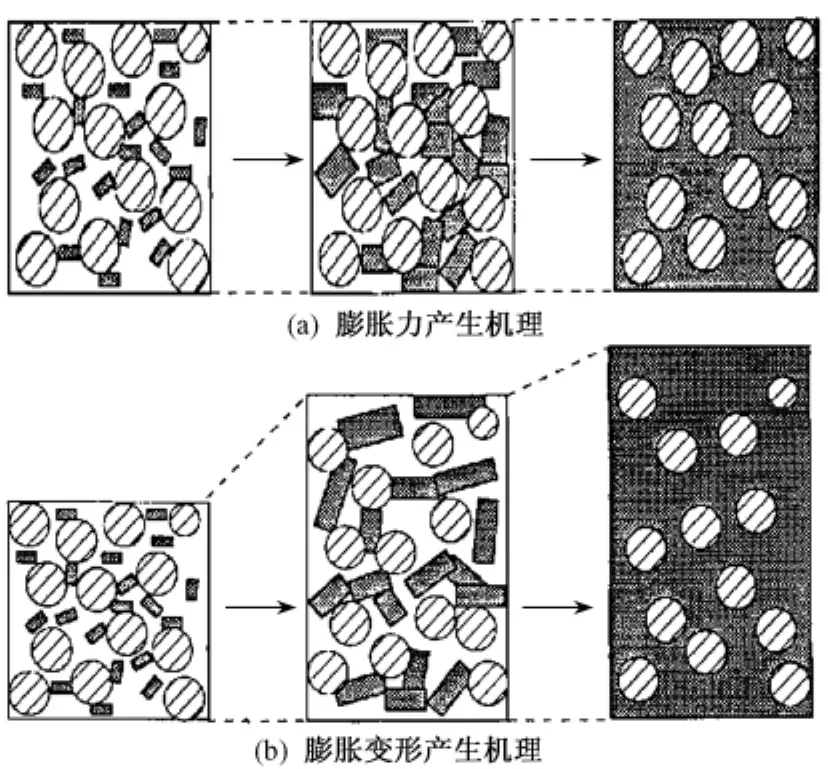
图2 膨胀土膨胀力及膨胀变形产生机理示意

可见，对于膨胀变形，其最终的稳态可以视为试样在新的干密度下的膨胀力试验，这样就可以忽略膨胀变形的过程，将膨胀变形的终态作为研究对象，从而可以统一考虑膨胀力试验与膨胀应变试验，进而从膨胀力的角度预测膨胀应变，即根据膨胀力的试验结果建立膨胀应变与对应荷载之间的关系。

2 膨胀应变模型的建立

由于将变形结束时的稳态作为研究对象，就需要一个指标来描述此时的状态，而且这个指标与膨胀应变及膨胀力都能建立联系。膨胀力试验中通常得到的都是膨胀力与干密度之间的关系，那么干密度可以作为这样的指标。

试样膨胀之前的初始干密度ρd0为

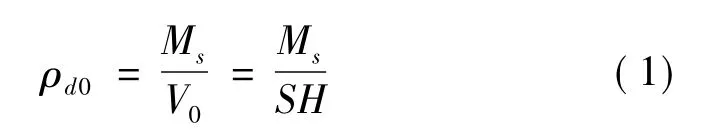
式中，Ms为试样中土粒的质量，V0为试样的初始体积，S和H分别为试样的底面积和高度。对于一维膨胀试验，则膨胀应变εz表示为

式中，ΔH为试样的膨胀量。

膨胀稳定时的体积为

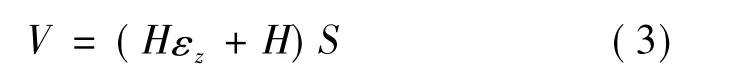
则此时的干密度为

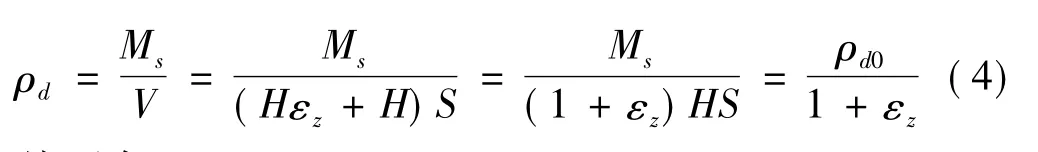
从而有

Komine［4］研究了 Kunigel-V1 土和 Neokunibond 土的膨胀力随干密度的变化趋势，若将干密度表示为膨胀力的函数，则分别为

式中，p为膨胀力。

基于前一节对膨胀变形和膨胀力试验的分析，可以将膨胀力试验中的干密度及其对应的膨胀力，分别作为膨胀变形试验终态时的干密度和外荷载，则可以将式(6)、式(7)分别代入式(5)，得到膨胀应变与外加荷载之间的关系:

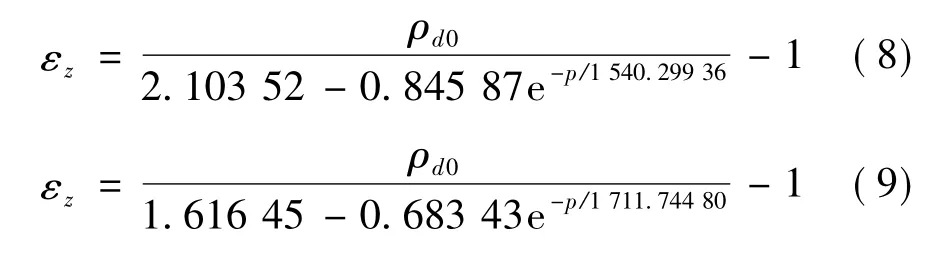
由式(8)、式(9)可知，膨胀应变随外加荷载的增大而减小，随初始干密度的增大而增大，这与众多试验结果一致［5-6］。

利用式(8)、式(9)分别对两种土的膨胀应变试验数据［4］进行拟合，结果如图3所示。

由图3可见，理论曲线与试验点基本吻合，表明所建模型的正确性，进而说明对于膨胀应变与膨胀力之间关系的分析较为合理。

对于Neokunibond土，膨胀应变较大(即100%)时，理论预测值较试验值小，由式(5)可知，说明此时的ρd由式(7)计算的理论值大于试验值，即当膨胀力与膨胀变形试验中的外荷载相同时，膨胀力试验中的干密度大于膨胀应变中的干密度。产生这种结果的原因很可能是由于土体细观结构的影响。试样产生宏观膨胀力的根本原因是蒙脱石颗粒晶层间的膨胀力，由于晶层间的膨胀力仅在垂直于晶层表面的方向显现，所以颗粒的取向会影响宏观膨胀力的大小。同样干密度条件下，如果颗粒大多趋向于水平方向，那么其产生的膨胀力会大于颗粒杂乱分布的情况，或者，如果产生同样大小的膨胀力，颗粒取向趋于水平的试样所需干密度会比颗粒杂乱分布试样的干密度小。

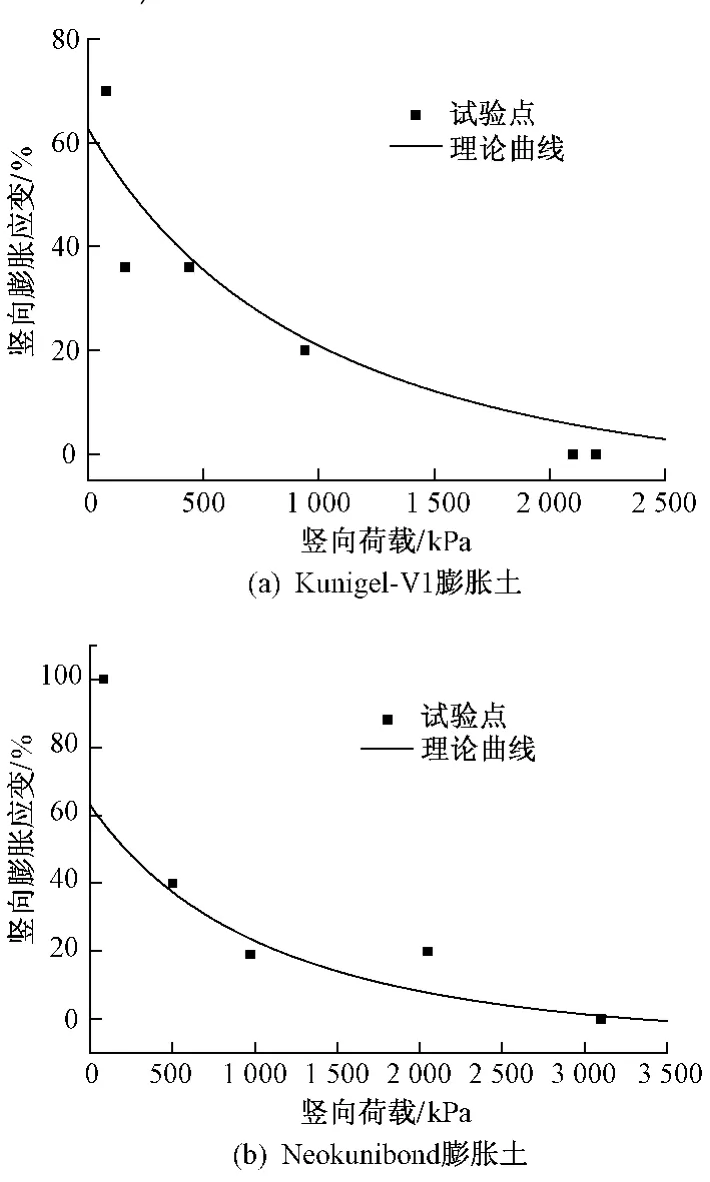
图3 膨胀应变模型拟合结果

由此看来，对于Neokunibond土膨胀应变为100%时的试验点，由于膨胀应变较大，细观结构变化会较大，膨胀应变试验中的颗粒取向比膨胀力中的更趋于水平，因此产生同样大小的膨胀力，其所需的干密度就较小，而膨胀力试验中的干密度会较大。根据式(5)可知，干密度ρd越大，膨胀应变越小，所以使得理论值较实际值小。

3 结论

通过分析膨胀变形和膨胀力的产生过程，发现膨胀变形的最终稳态可看作膨胀力试验。因此基于膨胀力试验结果得到了干密度与膨胀力之间的关系，进而从膨胀力的角度建立了膨胀应变与外加荷载之间的关系。所建立的理论模型能够较好地拟合试验结果，从而说明模型的正确，进而表明对于膨胀变形和膨胀力之间关系的分析是合理的。因此，可以将膨胀变形试验与膨胀力试验统一，通过膨胀力试验确定膨胀力，并预测膨胀应变。

另外，当膨胀变形较大时出现的预测误差是由于细观结构的变化较大引起的。

［1］ 陈伟．成绵乐铁路客运专线千佛山段膨胀土路堑滑坡浅析［J］．铁道建筑，2011(12):89-91．

［2］ 廖世文．膨胀土与铁路工程［M］．北京:中国铁道出版社，1984．

［3］ 杨庆．膨胀岩与巷道稳定［M］．北京:冶金工业出版社，1995．

［4］ KOMINE H，OGATA N．Predicting Swelling Characteristics of Bentonites［J］．Journal of Geotechnical and Geoenviromental Engineering，2004，130(8):818-829．

［5］ 陈孚华．膨胀土上的基础［M］．石油化学工业部化工设计院，译．北京:中国建筑工业出版社，1979．

［6］ KOMINE H，OGATA N．Experimental studyonswelling characteristics of compacted bentonite［J］．Canadian Geotechnical Journal，1994(31):478-490．