压实黏性土剪切破坏参数探讨

刘 军，刘俊新，赵海松，龙志伟

(西南科技大学土木工程与建筑学院，四川绵阳 621010)

通过三轴压缩试验，获取压实黏性土的应力—应变曲线，分析黏性土的破坏形式及压实黏性土的剪切破坏参数，为黏性土地基的处理提供参考。

1 静水压力试验

岩土材料在静水压力作用下表现出屈服特性，其压力p和体积应变εv的关系表现为三个阶段。在冲击荷载作用下，土体的变形较大。压力p和体积应变εv的关系见图1，试验参数为最大干密度ρdmax=2.02 g/cm3，最优含水率ωopt=12.54%，压实度为98%，含水率为12.54%，文中试样均相同。

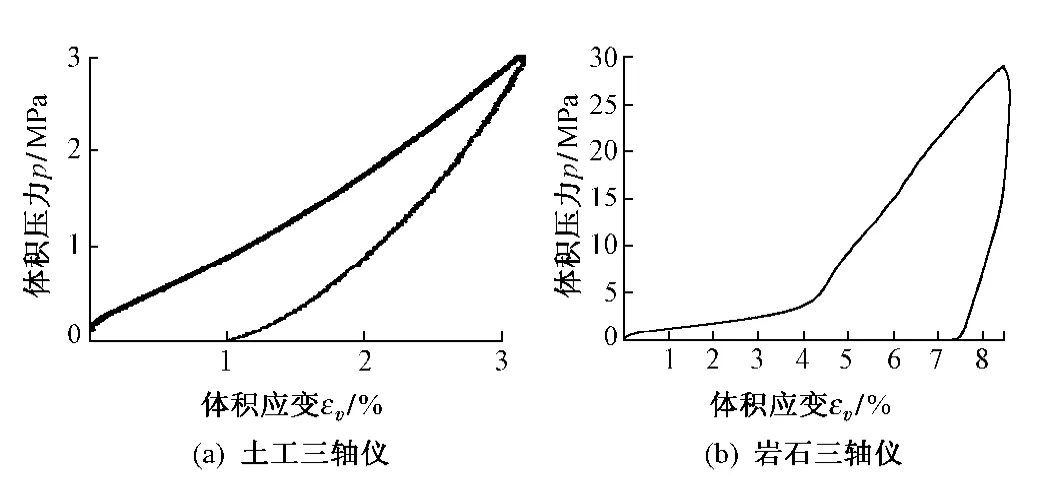
图1 静水压力试验应力—应变曲线

以屈服应力σ(k)为横坐标(k为硬化参数)，塑性体积应变［1-2］为纵坐标，并采用公式(1)对数据进行拟合(见图2和表1)。

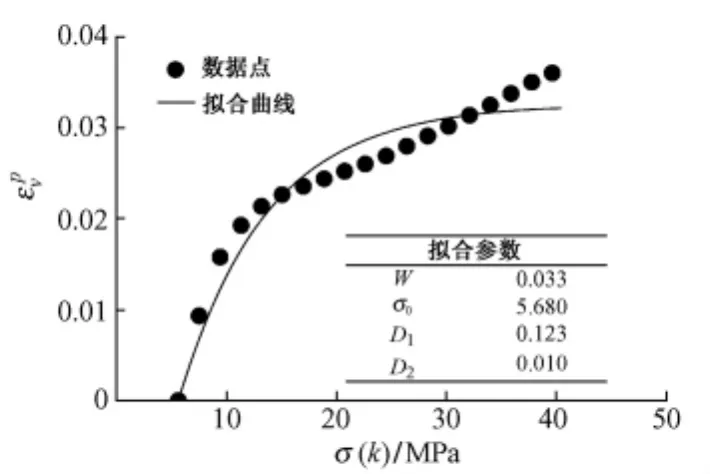
图2 屈服应力σ(k)与塑性体积应变拟合曲线

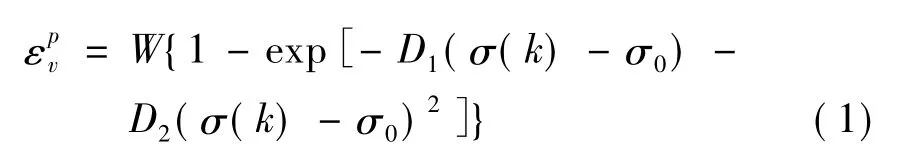
式中，W，D1，D2均为拟合参数。

经绘图比较，含水率为14.53%的曲线拟合较差，同时与理论计算的最大体积应变(假定水和固体颗粒不可压缩，孔隙水不从孔隙中排出)比较可知，其原因是由于含水率较大的试样，在试验过程中排出了大量孔隙水。

2 常规三轴压缩试验

压实黏性土发生的破坏形式为剪切破坏。为描述剪切破坏，就需确定剪切破坏面的形式及参数，所涉及的试验为常规三轴压缩试验。试样尺寸为φ39.1 mm×80 mm，在试验过程中加载采用变形控制，加载速率为0.5 mm/min，围压初步按0～1 200 kPa控制，试样的破坏形式为45°斜向剪切破坏，其应力—应变曲线见图3。

表1 拟合参数统计

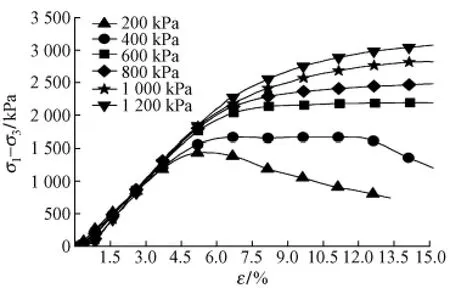
图3 不同围压下应力—应变曲线

2.1 模量参数的分析

对σ1=0的试验曲线的弹性段进行线性拟合，可获得其弹性模量，同时根据静水压力试验结果，按式(2)和式(3)计算出剪切模量G，结果见表2。

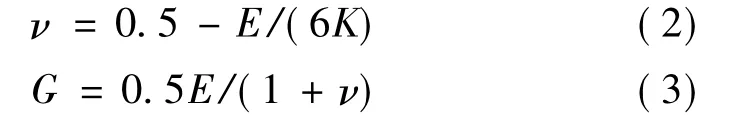
表2 模量统计

2.2 黏聚力和摩擦角的分析

根据上式可得到扭转和三轴拉伸与三轴压缩强度的比值Q1和Q2，由摩尔—库伦［4］公式小主应力σ3=σ1tan2(π/4－φ/2)－2ctan(π/4－φ/2)，考虑大主应力σ1=0可得到其单轴抗拉强度，具体参数见表3。

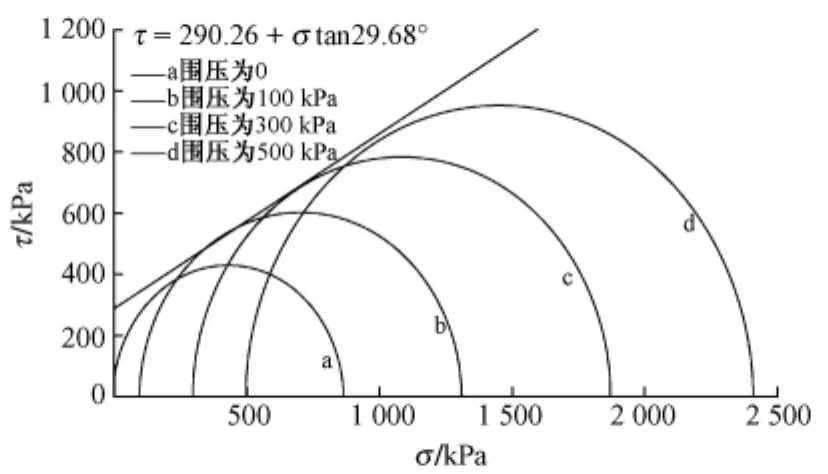
图4 摩尔应力圆

表3 黏聚力和摩擦角及Q1和Q2统计

2.3 剪切破坏面参数的分析

以J1=σ1+2σ3为横坐标，为纵坐标绘制曲线，同时采用［1，2］(－βJ1)+θJ1进行拟合(J'2为应力偏量第二不变量)，见图5，统计结果见表4。

图5 剪切破坏面拟合曲线

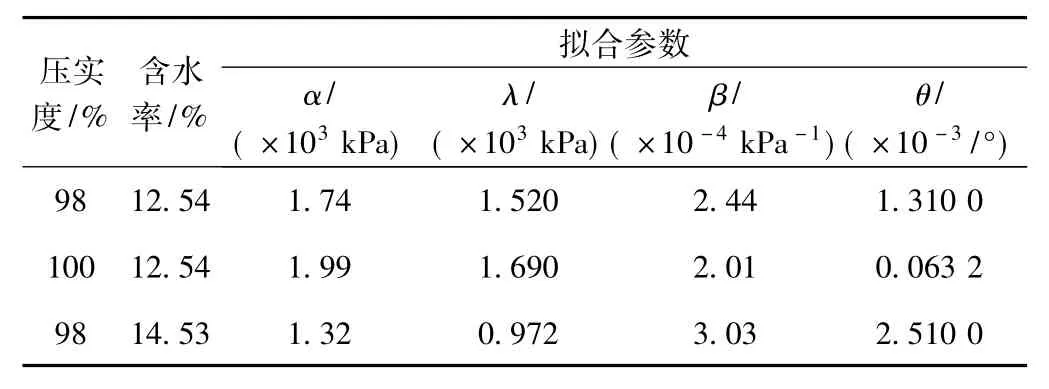
表4 剪切破坏面拟合参数统计

2.4 剪切运动硬化参数的分析

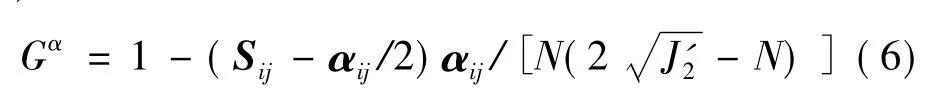
为了描述在峰值应力前土体的非线性弹性，引入式(6)式中，Gα为标量函数［1］;Sij为应力偏量;αij为背景应力张量，当αij=0即应力状态位于初始屈服面上时，Gα=1;当屈服面逼近破坏面时，Gα=0;N的大小为应力空间中破坏面与初始屈服面在轴的间隔。

以峰值强度的0.6倍时的应力为初始屈服应力，同时以较低应力偏量时应力偏量与塑性应变偏量曲线的直线段斜率作为cα值，对σ3=0的试验曲线进行分析。基于能量的损伤软化参数，损伤应力［5-6］定义为

式中，A，B为拟合参数;τ0为损伤的门槛值，当τ＜τ0时，d=0;τ 为应变能的函数［5-6］，定义为

利用式(8)，对σ3=0的试验曲线进行拟合，见图6和表5。

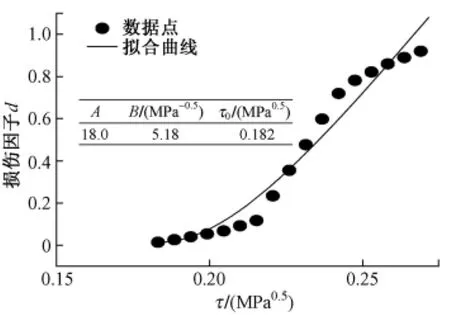
图6 基于能量损伤软化拟合曲线

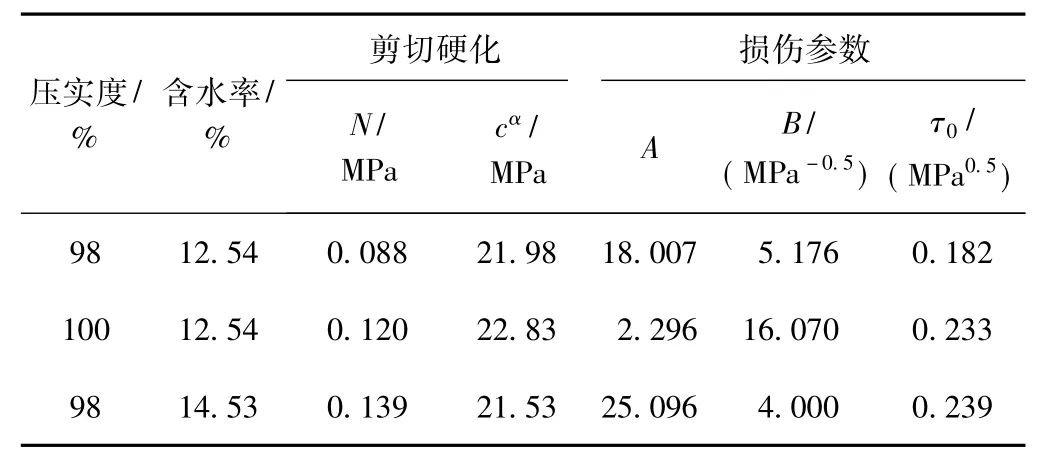
表5 剪切运动硬化及能量损伤拟合参数统计

3 结论

通过对黏性土的应力—应变关系、黏聚力和内摩擦角与含水量的关系等的曲线拟合分析表明，黏性土在碾压良好的情况下，在强夯施工前后密实度无明显提高［7-8］。而对于压实情况不好的地基，其夯击后密实度提高较大。主要结论如下:

1)通过静水压力试验获取了在静水压力下压实度与含水率的初始屈服强度和屈服应力与塑性体积应变的关系曲线，其应力—应变曲线较陡，黏性土表现为剪切破坏形式。

2)通过常规三轴压缩试验获得了不同压实度与含水率的弹性模量、黏聚力和摩擦角，由黏聚力和摩擦角换算得到扭转和三轴拉伸与三轴压缩强度比值Q1和Q2、剪切破坏面函数以及剪切运动硬化和基于能量损伤软化函数。

3)在地基处理中，由于黏性土在低围压条件下表现出软化现象，在高围压条件下表现出硬化现象，因此可以采取强夯法与振冲法相结合对地基进行处理。

［1］ SCHWER L E，MURRAY Y D．A three-invariant smooth cap model with mixed hardening［J］．International Journal for Numerical and Analytical Methods in Geomechanics，1994(18):657-688．

［2］ SCHWER L E．Continuous surface cap model for geomaterial modeling:a new ls-dyna material type［C］//7th International LSDYNA Users Conference，Michigan:LSTC，2002:16-50．

［3］ RUBIN M．Simple convenient isotropic failure surface［J］．Journal of the Engineering Mechanics Division，American Society of Civil Engineers，1991，117(2):348-369．

［4］ 袁聚云，钱建固，张宏鸣，等．土质学与土力学(第四版)［M］．北京:人民交通出版社，2009．

［5］ SIMO J C，JU J W．Strain and stress based continuum damage models-Ⅰ Formulation［J］．International Journal of Solids and Structures，1987，23(7):821-840．

［6］ SIMO J C，JU J W．Strain and stress based continuum damage models-Ⅱ Computational aspects［J］．International Journal of Solids and Structures，1987，23(7):841-869．

［7］ 唐勇，谢永利，程海涛．强夯压实法试验研究［J］．公路交通技术(应用技术版)，2006(4):82-84．

［8］ 郑晓，刘胜群．强夯法处理软弱地基工程实例分析［J］．铁道建筑，2008(4):59-60．