波流作用下悬浮隧道荷载研究

罗 刚，申 奇，周晓军，邓永杰

(西南交通大学交通隧道工程教育部重点实验室，四川成都 610031)

悬浮隧道(submerged floating tunnel，简称SFT)作为一种新型的海洋结构物，直接处于波浪、水流环境中。波浪荷载和水流荷载(以下简称波流力)为其主要的环境荷载，通常也是SFT结构设计的控制荷载和影响工程造价的主要因素［1］。工程上，一般不考虑波浪和水流的相互作用，将波浪荷载和水流荷载分别求解。但是，在水流作用下，波浪荷载将发生明显改变，可见在海洋工程结构荷载计算中必须正确考虑水流对波浪要素的影响［2］。作用于海洋结构物上的波流荷载计算主要有两种方法［3］:一是1950年由Morison等提出的经验公式计算法，主要用于计算结构物横向尺寸与波长相比较小时，作用在结构物上的波流力;二是1954年由MacCanmy和Fuchs提出的绕射理论。目前，基于该理论的数值方法主要是有限元法、边界元法等［4］。并已成功应用于海上大型结构物的波浪荷载计算和运动响应分析中。

1 结构计算模型

SFT作为一种直接处于波流作用下的大型水下交通结构，计算作用于其上的波浪荷载是SFT结构动力分析、结构可靠性分析和安全性评估的前提。悬浮隧道荷载计算模型如图1所示，为简化计算作如下假定:

1)SFT为固定不动的刚体，不考虑流固耦合作用。

2)规则波方向与SFT的纵轴线垂直(如图1中X轴方向)，来流为均匀恒定流。

3)采用Airy线性波浪理论，考虑一阶波浪力。

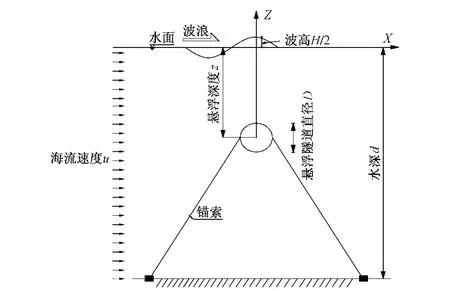
图1 荷载计算模型

2 计算公式推导

2.1 波流荷载简化计算方法

波流共同作用下，在自由表面以下深度为z处的任意单位长度水平SFT所受的水平波流力可以表述为［5］

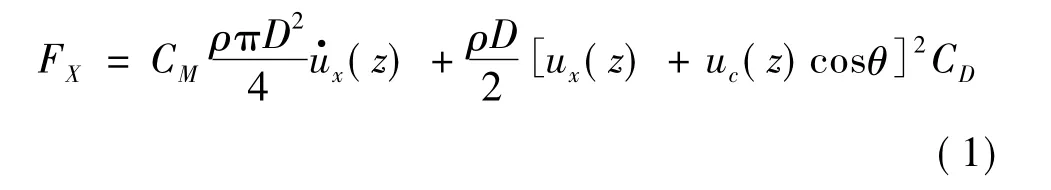
式中，CM为惯性力系数;CD为阻力系数;u·x(z)为SFT截面中心深度z处水质点加速度的水平分量;ux(z)为SFT截面中心深度z处水质点速度的水平分量;uc(z)为SFT截面中心深度z处水流速度;ρ为水密度;D为SFT直径;θ为水流与波浪方向的水平夹角。

当kD＜0.4π(k是波数)时，波流力直接采用Morison方程计算;kD＞0.4π时，Morison方程不再适用。此时，将SFT管段等效为M个周向小圆柱，如图2所示。

通过调整M的值，采用Morison方程仍能获得满意的结果。其中每个周向小圆柱体沿水平方向波流力为

图2 等效受力示意

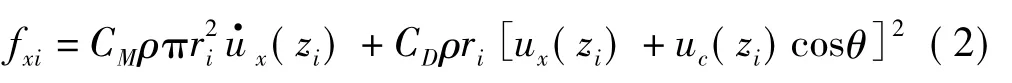
2.2 波流荷载公式推导

不考虑水流影响条件下，波长L和波的传播速度c可以表述为

式中，T为波周期;d为水深;L为波长;k=2π/L，为静水中的波数。

在均匀来流和波浪场的情况下，考虑到水流对波浪参数的影响，波的传播速度cx、波长Ls和波高Hs按下式计算:

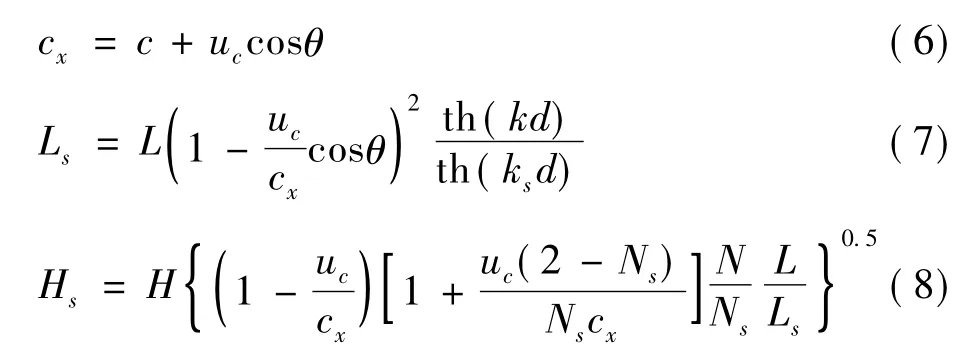
式中，uc为水流速度;ks=2π/Ls，ks为水流作用下的波数;H为静水中的波高;

根据Airy线性波浪理论，有波浪水质点的水平速度和加速度为［6］

式中，ωa=2π/T为圆频率，水流不影响波的周期。

将式(2)，式(4)～式(10)代入式(3)得到SFT波流力FX为

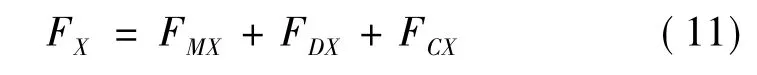
其中，

3 波流荷载影响因素分析

在进行SFT结构设计和稳定性分析时，往往更关注一个周期内波流力的极值(最大波流力)而忽略其出现的时刻。根据拟建悬浮隧道设计方案和环境条件［7-8］，讨论最大波流力与来流速度、悬浮隧道直径、悬浮深度、水深和波流夹角θ之间的关系，并引入一个无量纲变量，即折合波数kD，折合波数与波长的倒数成正比。

3.1 来流速度影响分析

为探讨流速与波流力之间关系，取流速分别为0，1.0 m/s，3.0 m/s和5.0 m/s，并假定环境条件为 H=9.3 m，D=25 m，z=30 m，d=200 m，θ=0°。此时，最大波流力与来流速度关系曲线如图3所示。

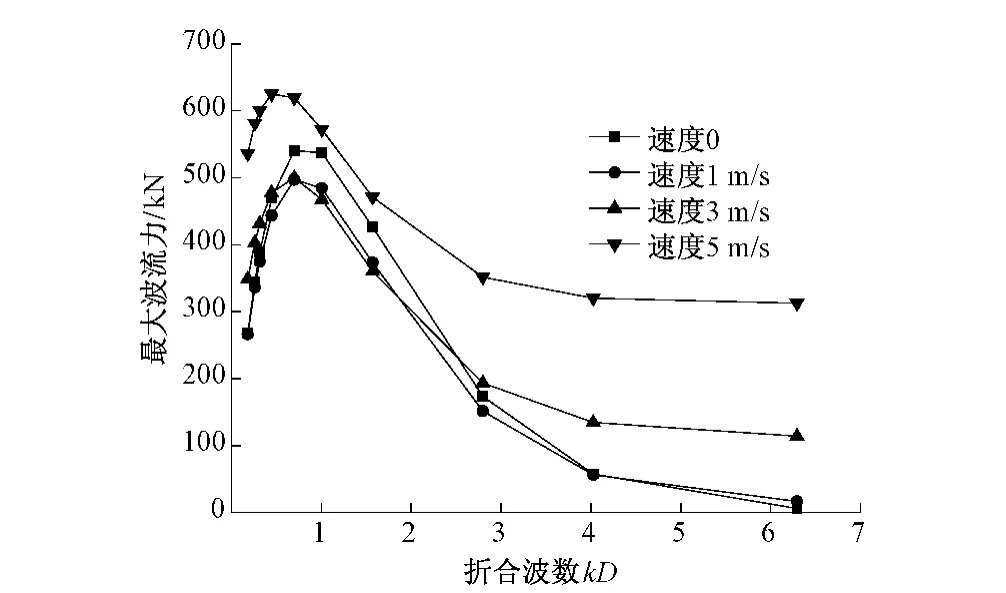
图3 最大波流力与速度的关系曲线

从图3可知，来流速度一定的情况下，随着折合波数增加，最大波流力先增后减;在折合波数相同，且当速度＜3 m/s时，随流速增加，最大波流力略有减小，当速度＞3 m/s时，随流速增加，最大波流力明显增加。可以理解为:当kD＜2.7时，随流速的增加，最大波流力先减小后增加;当kD＞2.7时，随流速增加，最大波流力增加。

3.2 SFT直径影响分析

为探讨SFT直径与波流力之间关系，取SFT直径分别为25 m，20 m，15 m和10 m，并假定环境条件为H=9.3 m，uc=3 m/s，z=30 m，d=200 m，θ=0°。此时，最大波流力与SFT直径的关系曲线如图4所示。

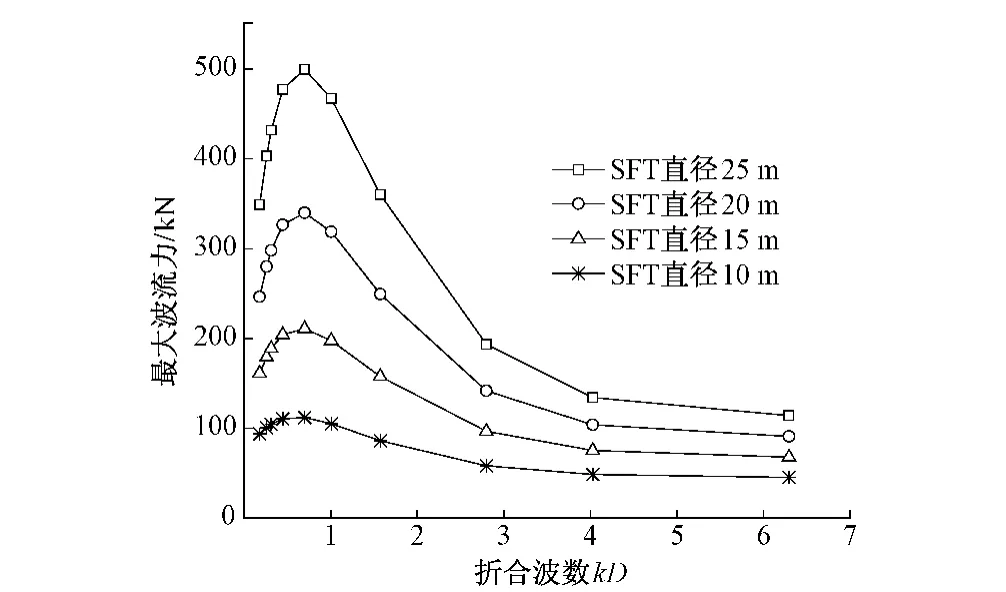
图4 最大波流力与SFT直径关系曲线

分析图4可知，当SFT直径一定时，随着折合波数增加，最大波流力先增加后减小;在折合波数一定时，随着SFT直径增加，最大波流力逐渐增加，且增加幅值较大。由此可见，SFT直径是影响SFT波流荷载的关键因素之一。

3.3 悬浮深度影响分析

为探讨SFT悬浮深度与波流力之间关系，取SFT悬浮深度分别为30 m，50 m和70 m，并假定环境条件为 H=9.3 m，uc=0 m/s，d=200 m，D=25 m。此时，最大波流力与SFT悬浮深度的关系曲线如图5所示。

图5 最大波流力与悬浮深度的关系曲线

由图5可知，在悬浮深度一定的条件下，最大波流力先增加后减少;在同一kD(或者同一波长)处，随着悬浮深度增加，最大波流力减小。当悬浮深度＞50 m且kD＞2.7时，悬浮深度几乎不影响最大波流力。相反，在悬浮深度＜50 m时，悬浮深度对最大波流力影响显著。

3.4 水深影响分析

为探讨SFT选址处水深与波流力之间关系，取选址处水深分别为50 m，100 m，150 m，200 m和250 m，并假定环境条件为H=9.3 m，uc=1.03 m/s，z=30 m，D=25 m，θ=0°。此时，最大波流力与水深的关系曲线如图6所示。

图6 最大波流力与水深的关系曲线

图6表明，在一特定水深下，随kD的增加，最大波流力先增加后减少;同一kD时，随水深增加，最大波流力减小。且当kD＞2时，水深对最大波流力的影响甚微。同时也可以看到，当水深＞100 m后，最大波流力几乎不受水深的影响。

3.5 波流夹角影响分析

为探讨波流夹角对波流力的影响，取波流夹角分别为0°，30°，60°和90°，并假定环境条件为 H=9.3 m，uc=3 m/s，D=25 m，z=30 m，d=200 m。此时，最大波流力与波流夹角的关系曲线如图7所示。

图7 最大波流力与波流夹角关系曲线

分析图7可知，最大波流力与波流夹角的关系比较复杂。当夹角＜60°时，随着夹角增大，最大波流力增加;当夹角＞60°时，随着夹角增大，最大波流力减小。分析其原因为水流对波浪要素有影响，导致波流力随波流夹角非线性变化。

4 结论

1)同向水流速度对SFT所受波流力影响比较复杂。当kD＜2.7时，随流速的增加，最大波流力先减小后增加;当kD＞2.7时，随流速增加，最大波流力增加。

2)SFT直径是影响SFT最大波流力的主控因素之一。直径越大，波流荷载越大。

3)SFT悬浮深度对最大波流力的影响显著，随悬浮深度增加，SFT最大波流力明显减少。当悬浮深度＞50 m时，最大波流力与悬浮深度的关系不大;当悬浮深度＜50 m时，悬浮深度是SFT所受最大波流力的主要影响因素之一。

4)水深对SFT波流荷载的影响在浅水区比较明显，当kD＞2时，水深对SFT波流荷载影响甚微。当水深＞100 m后，水深对最大波流力的影响可以忽略。

5)波流夹角对SFT波流荷载的影响很复杂。但可以确定各种不同波流夹角，最大波流力出现在同一波长(或kD)的波浪场中。

［1］ 麦继婷．波流作用下SFT的响应研究［D］．成都:西南交通大学，2005．

［2］ 任佐皋．波浪和水流对孤立桩柱共同作用力的计算［J］．海洋学报，1988，5(3):376-390．

［3］ 李玉成，腾斌．波浪对海上建筑物的作用［M］．北京:海洋出版社，2002:250-268．

［4］ KUNISU H．Evaluation of wave force on Submerged Floating Tunnels［J］．Procedia Engineering，2010(4):99-105．

［5］ 黄河宁．计算孤立桩柱上波流共同作用力的修正的Morison方程［J］．海洋学报，1991，13(2):290-294．

［6］ 潘锦嫦，李玉成．波浪与水流、地形综合作用下波浪变形理论及其在工程上的应用［J］．水运工程，1988(6):1-8．

［7］ 王广地，周晓军，高波．水下SFT波流荷载分析研究［J］．铁道建筑，2007(10):48-51．

［8］ 麦继婷，关宝树．琼州海峡SFT的可行性研究［J］．铁道工程学报，2003，12(4):93-96．