改进的粒子群模糊聚类方法

黄新建，牛 强

（中国矿业大学 计算机科学与技术学院，江苏 徐州221116）

0 引 言

模糊C均值聚类算法［1－2］（FCM）是目前使用最多的划分式聚类方法之一。由于FCM扩展了隶属度的取值范围，因此有着较好的数据表达能力和聚类效果［3］，且FCM的理论已相当完善，应用也比较广泛。但当数据集维数较高时，FCM存在聚类效果较差，很难找到全局最优等问题［4－5］。作为一种群体智能优化算法，粒子群优化算法 （PSO）的基本思想是通过种群在个体之间的信息共享和协同工作来寻找最优解。由于模糊聚类问题一定条件下可归结为优化问题［6］，已有很多学者提出了基于粒子群的模糊聚类算法［7－9］，Thomas A.Runkler等在文献 ［9］中提出了旨在保证模糊聚类约束条件的方法，解决了以隶属度对粒子进行编码时产生的问题。但基于粒子群的模糊聚类算法大多以聚类中心对粒子进行编码［10－11］，较少以隶属度对粒子进行编码。文献 ［9］中方法虽使隶属度满足了模糊聚类的约束条件，但仍然存在对噪音较敏感，处理样本数小于样本维数的数据时效果较差等问题。针对以上问题，在以隶属度对基于粒子群的模糊聚类算法进行编码的基础上，本文提出一种改进的隶属度分配方法。实验表明改进的方法较好地处理了含噪音的数据，并在样本数小于样本维数的数据上取得较之前方法更为理想的效果，较好地处理了低维数据和高维数据。

1 模糊C均值聚类算法

已知样本集X＝ ｛X1，X2，…，Xn｝有n个样本，分成C （2≤C＜n）类，其中Xi∈RP。FCM的目标函数为

m＞1为常数，ei（i＝1，2，…，C）为类i的聚类中心。μik（i＝1，2，…，C；k＝1，2，…，n）为样本k对类i的隶属度，满足

并给出式子

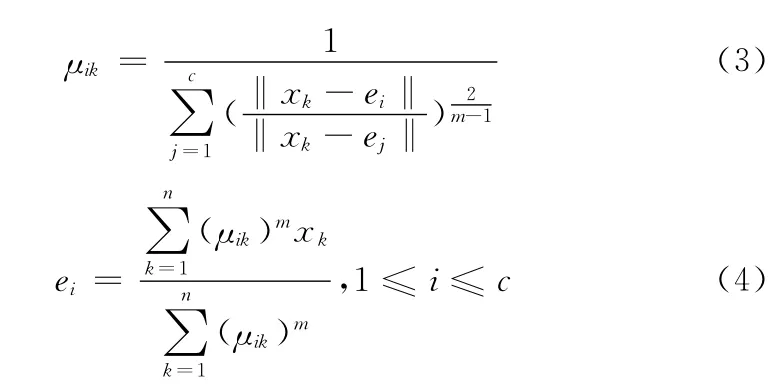
在式 （2）条件下通过反复迭代式 （3）和式 （4），使FCM的目标函数式 （1）取得极小值，即为FCM［12］。

2 基于粒子群的模糊聚类算法

2.1 PSO算法

D维空间中，有m个粒子，粒子i的位置为Xi＝ ［Xi1，Xi2，…，XiD］，飞行速度为Vi＝ ［Vi1，Vi2，…，ViD］，个体历史最优位置为Pi＝ ［Pi1，Pi2，…，PiD］，群体历史最优位置为Pg＝ ［Pi1，Pi2，…，PiD］，则用下式更新粒子的速度 和位置［13－14］

式 （5）和式 （6）中：i＝1，2，…，m——不同的粒子；C1、C2——大于0的学习因子，分别调节该粒子向自身历史最优位置和族群历史最优位置方向飞行的最大步长，取C1＝C2＝1.5；R1、R2为介于 ［0，1］之间的随机数；n为迭代次数［15］。

2.2 基于PSO的模糊聚类算法

设样本数为n，分成c类。PSO应用于模糊聚类并以隶属度编码时，粒子为n×c列的一维行向量，可表示为｛x11，x12，x1c，…，xn1，xn2，…，xnc｝，xij为样本i对类j的隶属度。采用隶属度编码时基本步骤为：先根据式 （4）求出粒子对应的聚类中心，后由该聚类中心和粒子值通过FCM的目标函数式 （1）求出粒子适应度。

至此，可得出基于粒子群的模糊聚类算法以隶属度编码时的流程如图1所示。

在计算聚类中心时，粒子的值需满足FCM的约束条件式 （2）。文献 ［9］中提出的约束方法为。

设wik为第样本k对类i的隶属度，算法运行时wik限定在 ［－5，5］内。计算粒子适应度时先采用sigmoid函数式（7）将 wik转化为uik∈ ［0，1］

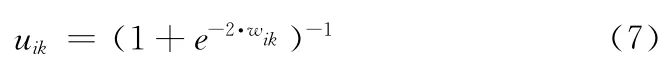
图1 基于PSO的模糊聚类流程

当样本对各类的隶属度之和不为1时，文献 ［9］的方法把不足或多出的部分平均地进行了增加或减少，对离样本近的类和离样本远的类同等对待，没有考虑样本与各个类之间的距离，收敛速度较慢，聚类效果较差。

本文提出的改进方法为：设uik为样本k对类i的隶属度，且uik∈ ［0，1］，li为样本k与类i的距离。≠1时，根据li决定uik增加或减少的幅度。

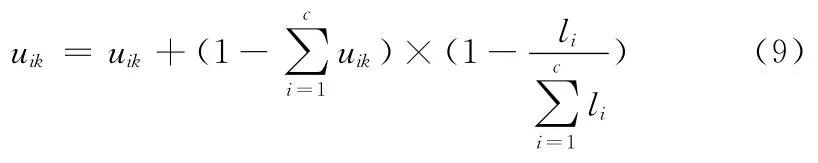
当样本对各类的隶属度之和不为1时，文献 ［9］的方法把不足或多出的部分平均地进行了增加或减少。本文改进方法考虑了样本与各类之间的距离关系，对于距离近的类，和小于1时隶属度加的多，和大于1时减的少；对于距离远的类，和小于1时隶属度加的少，和大于1时减的多。

保证约束条件的同时，改进方法在每次迭代均使样本向较相似的类进行靠近，同时远离差异较大的类，以加快收敛速度，提升聚类效果。每次约束时，改进方法增加了计算距离的运算过程，也省去文献 ［9］中方法需使用式（7）的转换过程。

3 实验测试与比较分析

实验分别使用了经典的FCM算法、文献 ［9］中方法以及本文的改进方法进行比较研究。使用的两组典型数据集来自文献 ［9］中比较方法时所使用的数据集，测试的数据集分别为：

（1）single outlier数据集： ［－1.2，0.5，0.6，0.7，1.5，1.6，1.7］，7组1维数据，其中 ［0.5，0.6，0.7］一类，［1.5，1.6，0.7］一类，－1.2为单异常点。

（2）lung cancer数据集：32组56维数据 （第4维和第38维中存在5个未知量，故只使用32组54维），分3类，第1类9组，第2类13组，第3类10组。

取粒子个数为10，迭代次数为100，表1至表2给出了运行各算法后对各项聚类指标取平均后的值，各表中的值具体体现了各方法的最优优化结果。其中DIC表示平均类内距离，DBC表示平均类间距离，OFV表示目标函数值，SCR表示成功分类率。

表1 Single Outlier数据集

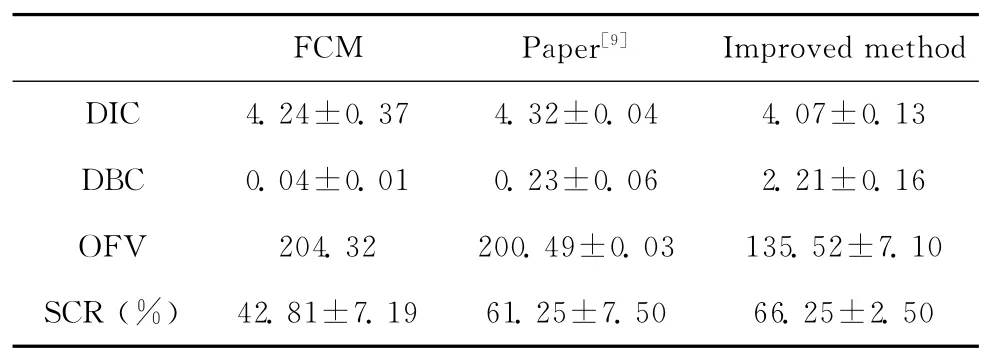
表2 Lung Cancer数据集

由表1知，当数据集含噪音时，本文改进方法同FCM一样在各种性能上优于文献 ［9］中方法，本文改进方法与FCM在小数据集中的差别并不明显。

由表2知，本文改进方法文献 ［9］中方法明显优于FCM，即基于PSO的FCM以隶属度编码时可较好处理样本维数大于样本数的数据集，且本文改进方法在样本维数大于样本数的数据集中的效果明显优于文献 ［9］中方法。

取粒子个数为10，迭代次数从1递增至100，随迭代次数的增加，图2至图5给出各方法的分类成功率和目标函数值的变化情况，各图体现出各方法随迭代次数的变化所取得的优化结果。其中DIC表示平均类内距离，DBC表示平均类间距离，OFV表示目标函数值，SCR表示成功分类率。

由图2及图3知，本文改进方法和FCM在各种性能上均优于文献 ［9］中方法，且与FCM在较小数据集上区别并不明显。相比FCM，本文改进方法在目标函数值中的波动较大，而在分类成功率中区别极小。

图4和图5表明此时FCM效果较差，即基于PSO的FCM以隶属度编码时较FCM有明显优势。同时本文改进方法显著优于文献 ［9］方法，即本文方法在样本维数大于样本数的数据集中明显优于文献 ［9］中方法。

图5 Lung cancer数据集目标函数值比较

综上所述，由single outlier数据集实验知，相比本文改进方法和FCM，文献 ［9］中方法对噪音较敏感，本文改进方法在小数据集中与FCM差别不大；由lung cancer数据集实验知，FCM对于样本维数大于样本数的数据集聚类效果较差，基于PSO的FCM以隶属度编码时可较好解决，同时本文改进方法优于文献 ［9］中方法。可知，本文改进方法在不同数据集中都优于文献 ［9］中方法，显著提升了聚类效果，进一步加快了收敛速度。

4 结束语

针对基于PSO的FCM以隶属度编码时出现的问题，本文改进了之前实现约束条件的方法。之前基于PSO的FCM以隶属度编码时不能较好地处理含噪音的数据集以及样本维数大于样本数的数据集。实验表明本文的改进方法较之前方法可较好地处理噪声，并进一步提升了在样本维数大于样本数的数据集上的聚类效果，取得了较优的效果，使得基于PSO的FCM以隶属度编码时也可较好地处理含噪音的数据和样本维数大于样本数的数据集。

［1］SUN JG，LIU J，ZHAO LY.Clustering algorithms research［J］.Journal of Software，2008，19 （1）：48－61 （in Chinese）.［孙吉贵，刘杰，赵连宇.聚类算法研究 ［J］.Journal of Software，2008，19 （1）：48－61.］

［2］TANG Chenglong，WANG Shigang，XU Wei.New fuzzy c－means clustering model based on the data weighted approach ［J］.Data ＆Knowledge Engineering，2010，69 （9）：881－900.

［3］QU FH.Researeh on fuzzy clustering algorithm and its applieation ［D］.Changchun：Jilin University，2009 （in Chinese）.［曲福恒.一类模糊聚类算法研究及其应用 ［D］.长春：吉林大学，2009.］

［4］CAI WL，CHEN SC，ZHANG DQ.Fast and robust fuzzy c－means clustering algorithms incorporating local information for image segmentation ［J］.Pattern Recognition，2007，40 （3）：825－833.

［5］KANG Jiayin，MIN Lequan，LUAN Qingxian.Novel modified fuzzy c－means algorithm with applications ［J］.Digital Signal Processing，2009，19 （2）：309－319.

［6］LI JJ，XIANG Y，LU YM，et al.Survey of particle swarm clustering algorithms ［J］.Application Research of Computers，2009，26 （12）：4423－4427 （in Chinese）. ［李峻金，向阳，芦英明，等.粒子群聚类算法综述 ［J］.计算机应用研究，2009，26 （12）：4423－4427.］

［7］WEN ZW，LI RJ.Fuzzy c－means clustering algorithm based on improved PSO ［J］.Application Research of Computers，2010，27 （7）：2520－2522 （in Chinese）. ［温重伟，李荣钧.改进的粒子群优化模糊C均值聚类算法 ［J］.计算机应用研究，2010，27 （7）：2520－2522.］

［8］LI LL，LI M，LIU XY.Image segmentation algorithm based on particle swarm optimization fuzzy c－means clustering ［J］.Computer Engineering and Applications，2009，45 （31）：158－160（in Chinese）.［李丽丽，李明，刘希玉.基于粒子群模糊C－均值聚类的图像分割算法 ［J］.计算机工程与应用，2009，45 （31）：158－160.］

［9］Thomas A Runkler，Christina Katz.Fuzzy clustering by particle swarm optimization ［C］.Vancouver，BC，Canada：IEEE International Conference on Fuzzy Systems，2006：601－608.

［10］PU PB，WANG G，LIU TA.Research of improved fuzzy c－means algorithm based on particle swarm optimization ［J］.Computer Engineering and Design，2008，29 （16）：4277－4279（in Chinese）.［蒲蓬勃，王鸽，刘太安.基于粒子群优化的模糊C－均值聚类改进算法 ［J］.计算机工程与设计，2008，29 （16）：4277－4279.］

［11］YANG GQ，ZHU CM.Particle swarm optimization algorithm based fuzzy kernel clustering method ［J］.Journal of Shanghai Jiaotong University，2009，43 （6）：935－939 （in Chinese）.［杨广全，朱昌明.基于粒子群优化的模糊核聚类方法 ［J］.上海交通大学学报，2009，43 （6）：935－939.］

［12］NIU Q，XIA SX，ZHOU Y，et al.Improved fuzzy c－means clustering algorithm ［J］.Journal of University of Electronic Science and Technology of China，2007，36 （6）：1258－1259 （in Chinese）.［牛强，夏士雄，周勇，等.改进的模糊C－均值聚类算法 ［J］.电子科技大学学报，2007，36 （6）：1258－1259.］

［13］HUANG SR.Survey of particle swarm optimization algorithm［J］.Computer Engineering and Design，2009，30 （8）：1977－1980（in Chinese）. ［黄少荣.粒子群优化算法综述［J］.计算机工程与设计，2009，30 （8）：1977－1980.］

［14］WANG JW，LI HN.Summary of particle swarm optimization algorithm ［J］.Modern Computer，2009，26 （2）：22－27（in Chinese）.［王杰文，李赫男.粒子群优化算法综述 ［J］.现代计算机，2009，26 （2）：22－27.］

［15］WANG XF.Research on dynamic topology of particle swarm algorithms［D］.Chongqing：Southwest University，2008（in Chinese）.［王雪飞.粒子群算法的动态拓扑结构的研究［D］.重庆：西南大学，2008.］