基于条块拼接的快速纹理合成

邹 昆，沃 焱，张见威

（1.电子科技大学 中山学院计算机学院，广东 中山528402；2.华南理工大学 计算机科学与工程学院，广东 广州510006）

0 引 言

纹理映射是计算机图形学中增加计算机生成模型的真实感的一种重要方法。基于样图的纹理合成［1－3］可以根据给定的样图生成任意大小的相似纹理，解决了纹理映射中因纹理尺寸不足所引起的接缝和走样问题。与过程纹理合成相比，其生成模型的适用范围更广，且无需复杂的参数调试，因此成为近年来的一个研究热点。

基于样图的合成算法可分为逐点合成［4－7］和逐块合成［8－14］两类，逐块合成算法在速度和结构特征保持方面更有优势。对于这两类算法，匹配点/块的搜索通常是其瓶颈，一种加速方法是优化匹配搜索过程［11－12］，另一种加速方法是通过预处理来缩小合成时的搜索范围甚至免除匹配搜索。如文献 ［9］通过在预处理阶段计算得到一组优选位移，来大幅缩小合成时匹配块的搜索范围。而Zelinka［4］在预处理阶段计算得到一个Jump Map，可通过其查找样图中与任一像素具有相似邻域的像素，合成时通过连续拷贝像素以及在相似邻域像素间的跳转来完成合成。

在已有的大量基于样图的纹理合成算法中，大多数是离线的［4－6，9－14］，即 提 前 合 成 好 所 需 要 的 纹 理 ， 将 输 出 保 存起来供渲染时使用。离线纹理合成算法的一个问题是当合成纹理较大时，要占用较多存储空间，特别是当待渲染场景需要很多不同的纹理图时。在2010年的SIGGRAPH上，Lefebvre等［8］提出了一种基于图的纹理合成算法，根据可生成纹理空间建图，并将纹理合成转化为该图中的最短路径搜索问题，合成完成后，仅需要保存得到的路径，合成的纹理可在渲染时实时重建，这样就节省了大量内存空间。然而该方法仅适用于建筑纹理，在合成更具一般性的纹理时不能较好地保持纹元特征。

本文基于 Lefebvre算法［8］，并结合 Zelinka［4］提出的基于Jump Map的合成算法中跳转的思想，以及文献 ［9］中预先计算优选位移的思想，提出一种新的纹理合成算法。与文献 ［8］类似，通过相继沿垂直和水平方向通过对样图中的条块重组进行合成，区别在于没有建图并进行最短路径搜索，而是在预处理中计算原图在垂直和水平两个方向上的平移误差，得到与误差较小的平移间距对应的平行切割集，在合成时按照与误差相关的概率值选择增长或在平行切割间跳转来完成合成。该算法对于在两个主方向上具有平移相似性的纹理具有很好的合成效果，合成过程因无需匹配，速度很快，合成完成后仅需保存与垂直和水平拼接方案所对应的两组切割集，占用空间小。

1 Lefebvre纹理合成算法

假定样图I为W×H像素，待合成图像为WT×HT像素。Lefebvre算法的合成过程由两个方向的合成组成，先沿垂直方向合成出W×HT的中间图，再以此中间图为样图，沿水平方向合成出WT×HT的目标纹理。由于两个方向合成类似，在此以水平方向为例介绍其单方向的预处理和合成过程，然后简介双方向合成。

1.1 预处理

预处理阶段的主要任务是，对于每个整数σ∈ ［1，W－1］，在样图中查找相距σ像素的平行切割并添加到集合C。图1给出了σ＝100时的一对平行割。平行切割的误差为c和c‖右边像素的误差之和

式中：p——预定义的常数。该误差为c的左部和c‖的右部的拼接误差，也是c‖的左部和c的右部的拼接误差。在合成过程中可能发生从c到c‖的跳转或从c‖到c的跳转，前者将c的左部和c‖的右部拼接，后者将c‖的左部和c的右部拼接。

在查找平行割时，需要δ（c，c‖）尽可能小。其步骤如下：

（1）计算得到一个 ［W－σ］×H的误差图Eσ，Eσ（x，y）＝‖I（x，y）－I（x＋σ，y）‖p；

（2）使用动态规划在Eσ中寻找一条最小误差路径π（从上至下，y值单调递增）；

（3）如果π的误差为∞，则结束。否则将π对应的一对平行切割添加到C中，并将Eσ中与π相距σ以内的像素值设为∞，然后返回步骤 （2）。

1.2 单方向合成

图1 相距100像素的平行割

合成结果由样图中的条块拼接而成，每一种拼接方案对应于一系列切割c＊，c0，c0‖，…，cn，cn‖，c＋，其中c＊和c＋是由用户指定的起始和终止切割，默认对应于原图的第一和最后一列，而ci和ci‖分别是前一条块的终止切割和下一条块的起始切割。合成过程可以看成是从c＊开始，逐步添加切割到合成图中，如图2所示。在某一时刻，当前终止割为ca时，接下来有两种选择：要么增长当前条块至ca的后继切割 （绿色表示），要么通过跳转到与ca平行的切割ca‖（红色表示）而拼接一个新的条块。前者代价为0而后者代价为δ（ca，ca‖）。这样可以创建一个图G＝ （C×Z，E＜∪E‖）来表示所有可能的合成方案，其中每个结点（c，z）∈C×Z代表切割c在合成图中放置在横坐标z处，而E＜和E‖分别表示增长边和跳转边集合，与之前的两种选择相对应。图G每条从结点 （c＊，）到结点（c＋，WT）的路径都对应一种拼接方案，其误差为路径上所有跳转边的代价和，这样合成问题就转化为最短路径搜索问题。

图2 通过添加切割进行合成［8］

1.3 双方向合成

合成的最终目标是合成WT×HT的图像，这通过先沿垂直方向进行单方向合成，再沿水平方向合成来实现，其中第二步使用前一步的结果作为样图。为了快速计算出中间结果的切割集，在预处理阶段，对于每一σ，保存与Eσ对应的路径图 （与Eσ相同大小，记录了在每个像素位置处的最小误差路径走向），以及每条最小误差路径的起始位置，完成垂直方向合成后，将其拼接方案应用于每一路径图，根据路径起始位置快速算出新的路径 （误差不一定最小），并重新计算每条路径的误差。

2 本文合成算法

2.1 算法基本思想

Lefebvre算法仅适用于建筑纹理合成，对于更具一般性的纹理合成效果较差，分析其主要原因如下：

（1）在添加平行切割路径时仅考虑了局部匹配误差，不能较好地保持大尺度特征，如当平行切割间距σ与纹理的周期性相违背时，相对应的跳转会带来明显的瑕疵；

（2）合成过程限定了起始和终止位置，这种控制很容易违背纹理的周期性，为了满足这种限定条件容易在最短路径中包含误差较大的边。

为了提高一般纹理的合成质量，在预处理中查找平行切割时对σ做了限制，仅对整体匹配误差较小的σ值查找平行切割；另外摒弃了基于图的合成过程，仍然通过添加切割的方式进行合成，但合成至某一切割时，是增长当前块至其后继切割还是跳转到其平行切割是通过误差大小相关的概率值来判定。

2.2 预处理

预处理阶段的主要任务是计算得到水平和垂直方向一组误差较小的切割路径，在此以水平方向为例 （针对水平方向合成，切割为垂直方向）。

2.2.1 最小误差平移距离集计算

将样本I沿水平方向平移σ像素后得到Iσ（如图3所示），其与平移前I的重叠区域的逐像素误差其实正好等于Lefebvre算法中的误差图Eσ中的像素值，在此针对每一σ计算其整体误差 （为了便于加速将p值取2）

然后取前N个误差最小的σ值构成集合TH。为保持大尺度特征，避免特征拖曳，限制σ值于区间 ［0.1W，0.9W］内。由于

等式右边前两项为矩形区域的像素值平方和，可用平方和查找表 （SST）［15］加速，最后一项I（x＋σ，y）可改写为I－（W－σ－1－x，y）（其中I－为将样本I左右翻转后得到的图像），即H个一维卷积之和，可用FFT进行加速。

2.2.2 切割集计算

图3 I与Iσ的重叠区域及一条切割路径p

针对每一σ∈TH，使用和1.1节中相同方法计算平行切割 （每对平行切割对应于重叠区域的一条最小误差路径，如图3中p所示），将它们添加到切割集CH，同时保存平行切割的误差δ（c，c‖）。为了保证平行切割的误差不至于过大，在计算同一重叠区域的多条切割路径时，要求它们的误差不得超过第一条路径的20%，超过则结束与当前σ值对应的平行切割查找过程。

针对垂直方向用类似的方法计算TV和CV。

2.3 合 成

在此首先以水平方向为例，介绍从样图I合成WT×H目标图的单方向合成算法。定义切割c的后继切割为与c不交叉且在I中位于c右方的切割。将I的第一列也看成切割。定义从切割c0跳转到其平行切割c0‖的概率为

这样误差最小的切割跳转概率最大。算法描述如下：

（1）设已合成长度L＝0，设合成切割表LH为空；设当前切割c为I的第一列，并将c添加至LH。

（2）若当前切割c没有后继切割 （如图4中c1‖和c3‖），则转 （3），否则随机选取一个最前后继切割c’（图4中c1和c2均为第一列的最前后继切割），将c到c’间的条块拼贴至合成图，设L＋＝c’min－cmin，c＝c’，若L≥WT－1，则算法结束，否则转 （4）。

（3）若L＋W－1－cmin≥WT－1，则将c右方的条块拼贴到合成图中，算法结束；否则将c添加至LH，并执行跳转，即设c＝c‖，转 （2）。

（4）产生一 ［0，1］内的随机数r，若r＜P（c→c‖），则将c添加至LH，并跳转 （即设c＝c‖），转 （2）；否则直接转 （2）。

为进一步增加合成的多样性，在第 （1）步中可随机选择一切割为当前切割c，并设L＝cmin－cmax。上述算法最终得到一切割序列，其形式如LH＝ ｛c＊，c1，c2…cn｝，其中c＊为起始切割，后面均为执行跳转的切割，合成图的构成为：从到c1的条块，从c1‖到c2的条块，…，cn‖右方的块。

在由单方向合成向双方向合成的扩展方面和Lefebvre算法相同，先沿垂直方向合成，然后沿水平方向合成，并采用了类似的加速算法计算中间结果的切割集，只不多仅需对N个σ值保存对应的路径图。

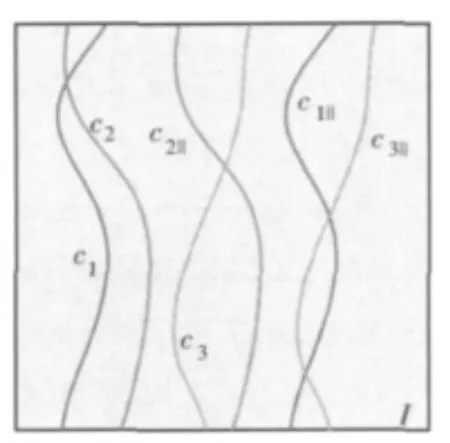
图4 I中所有c∈CH的示意图（为简单起见假设仅3对）

合成完毕后，仅需保存两个方向的切割序列LH和LV。在渲染时对于给定的纹理坐标 （x，y），根据LH和x可确定其对应于中间图的像素坐标 （x0，y），然后再根据LV和y可确定其对应于样图的像素坐标 （x0，y0），如图5所示（仅显示了2对切割）。

3 实验结果

用PC机 （Intel Core 2Duo CPU T5750 2.00G/2G）对一些纹理进行了合成，图6中为样图，其中包括随机纹理、半规则纹理和规则纹理。图7给出了使用Lefebvre算法和本文算法的合成结果，合成图大小均为256×256像素。在使用Lefebvre算法合成时，起始切割和终止切割分别设为第一行/列和最后一行/列，在使用本文算法合成时，绳网和面包的N值取5，饮料罐N值取4，飞狮N值取3。表1中是相应的时间数据。

可以看到，Lefebvre算法的合成结果中存在特征拖曳、重复或丢失的情况，这是由于在计算切割时没有考虑大尺度特征保持所造成的，本文算法的合成效果明显更优。在时间方面，本文算法的预处理速度有十几倍的提升，这归功于FFT加速以及切割计算次数的减少，合成速度更是有几十倍的提升，因为无需进行任何匹配操作，如图7所示。

图7 合成结果对比

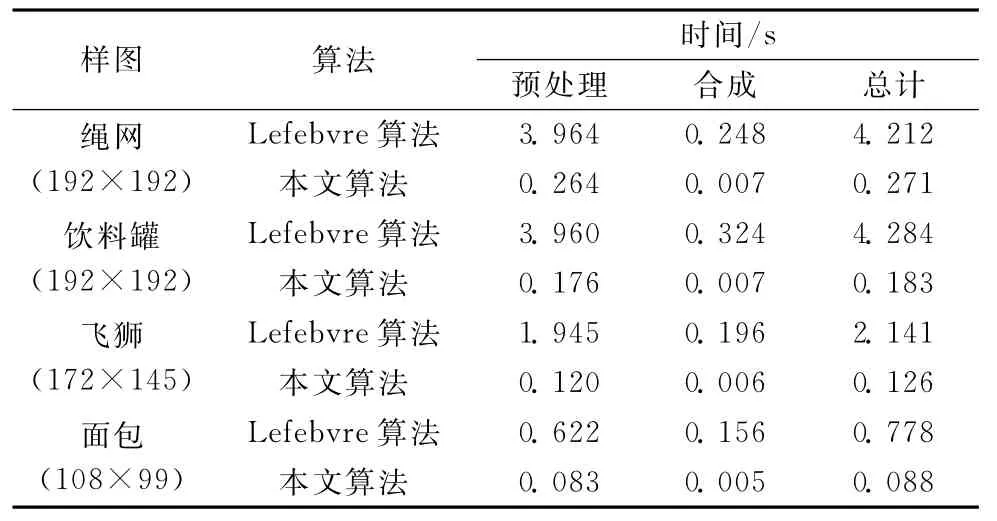
表1 图7中纹理的合成时间数据

4 结束语

本文在Lefebvre算法基础上提出一种新的基于条块拼接的快速纹理合成算法，通过在计算切割路径时考虑整体匹配误差，使得对一般纹理的合成质量大幅提高，在合成时改路径搜索为随机跳转，增加了合成结果的随机性，合成速度也有几十倍的提升。该算法对于具有水平和垂直平移相似性的纹理具有较好的合成效果，且合成结果可以紧凑的方式保存，在渲染时实时重建。

［1］WEI L Y，Lefebvre S，Kwatra A，et al.State of the art in example－based texture synthesis ［R］.Eurographics State of The Art Report Eurographics Association，2009.

［2］ZHU Wenhao，WEI Baogang.The technology of sampledbased texture synthesis ［J］.Journal of Image and Graphics，2008，13 （11）：2063－2069 （in Chinese）. ［朱文浩，魏宝刚.基于样本的纹理合成技术综述 ［J］.中国图象图形学报，2008，13 （11）：2063－2069.］

［3］XUE Feng.Research on texture synthesis from sample ［M］.Hefei：Hefei Univerity of Technology Press，2007 （in Chinese）.［薛峰.基于样图的纹理合成技术研究 ［M］.合肥：合肥工业大学出版社，2007.］

［4］Zelinka S，Garland M.Jump map－based interactive texture synthesis［J］.ACM Transactions on Graphics，2004，23 （4）：930－962.

［5］ZOU Kun，HAN Guoqiang，LI Wen，et al.Multiresolution texture synthesis using real－time pattern matching ［C］.Proceedings of the IEEE International Conference on Robotics and Biomimetics.Sanya，China：IEEE Press，2007：1327－1332.

［6］LI Dajin.Controllable consecutive multi－scale texture synthesis［J］.Computer Engineering，2009，35 （24）：211－212 （in Chinese）.［李大锦.可控的连续多尺度纹理合成 ［J］.计算机工程，2009，35 （24）：211－212.］

［7］Lefebvre S，Hoppe H.Appearance－space texture synthesis ［C］.New York，NY，USA：ACM SIGGRAPH，2006：541－548.

［8］Lefebvre S，Hornus S，Lasram A.By－example synthesis of architectural textures［C］.Los Angeles：ACM SIGGRAPH，2010.

［9］ZOU Kun，HAN Guoqiang，LI Wen，et al.An efficient method of texture synthesis based on Graph Cuts ［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2008，20（5）：652－658 （in Chinese）.［邹昆，韩国强，李闻，等.基于Graph Cut的快速纹理合成算法 ［J］.计算机辅助设计与图形学学报，2008，20 （5）：652－658.］

［10］CHEN Xin，WANG Wencheng.Reusing partially synthesized textures for real－time synthesis of large textures ［J］.Chinese Journal of Computers，2010，33 （4）：768－775 （in Chinese）.［陈昕，王文成.基于复用计算的大纹理实时合成 ［J］.计算机学报，2010，33 （4）：768－775.］

［11］CAI Zhilin，XU Wenbo，SUN Jun.Quick texture synthesis based on searching matching patch along spiral path ［J］.Computer Engineering and Design，2010，31 （23）：5052－5055（in Chinese）.［蔡志林，须文波，孙俊.螺旋线状搜索的快速块匹配纹理合成 ［J］.计算机工程与设计，2010，31（23）：5052－5055.］

［12］LI Yan，WANG Yongdong，WU Wenzhi，et al.Patch－based texture synthesis by searching matching patch along spiral path［J］.Computer Engineering，2006，32 （16）：210－212 （in Chinese）.［李燕，王永东，吴文治，等.螺旋状匹配搜索的块拼贴纹理合成 ［J］.计算机工程，2006，32 （16）：210－212.］

［13］YU Yongsheng，GU Yaolin.Improved method based on Ashikhmin and Kong texture synthesis algorithms ［J］.Computer Engineering and Design，2007，28 （2）：395－396 （in Chinese）. ［余永胜，顾耀林.基于Ashikhmin和Kong纹理合成算法的改进方法 ［J］.计算机工程与设计，2007，28 （2）：395－396.］

［14］SUN Yan，CHEN Yong.Texture synthesis based on gradient［J］.Computer Engineering and Design，2007，28 （1）：118－120（in Chinese）.［孙岩，陈勇.基于梯度的纹理合成 ［J］.计算机工程与设计，2007，28 （1）：118－120.

［15］Kilthau S L，Drew M，Moller T.Full search content independent block matching based on the fast Fourier transform ［C］.New York：International Conference on Image Processing，2002：669－672.