基于多视点立体角度模型的相关研究

程 浩 安 平 张兆杨 李贺健 张之江

(新型显示技术及应用集成教育部重点实验室 上海 200072)

(上海大学通信与信息工程学院 上海 200072)

1 引言

目前，多视点显示技术(也称为裸视立体显示)因其无需佩戴任何辅助设备就可以直接观看显示器上的3维图像的特点而广受关注。将其与多视点视频显示相结合就可大幅度扩大立体视角、增强立体感、且人眼不易疲劳。自由视点电视(Free-viewpoint TV, FTV)已被认为是未来 3维显示技术的发展方向[1]。

目前FTV技术还不完善，正处在发展阶段。文献[2]从FTV整体框架出发对FTV进行了比较全面的回顾和分析；可以使用两个摄像机加TOF相机(Time-Of-Flight camera)的模式来代替摄像机阵列，这样构建的立体显示系统也取得了不错的效果[3,4]。Smolic等人[5]对拍摄好的3D片源进行后期制作和加工来增强其观看效果。文献[6]等在降低多视点编码复杂度上进行了深入的研究。然而目前多视点系统研究多为建立系统后的定性分析，由于未进行模型构建，所以只能通过反复探索性试验来获得最终结果，这样的结果因缺乏理论支持，不具有普适性。近几年来，国内外研究已经开始涉及多视点立体显示模型。其中文献[7]从计算机图形学的角度建立立体显示数学模型，但尚未考虑摄像机焦距等因素，无法精确控制真实的拍摄过程；文献[8]建立了多视点立体显示模型，但没有涉及到多视立体视角。

本文从多视点立体显示的系统映射关系着手，建立多视点立体视角模型，该立体角与物体的深度和观看距离存在定量关系。但因受到人眼融合极限的制约，因而给出在实际拍摄时的立体角范围进而推导出在理想情况下视点数N与最大立体视角之间的关系。本文的结果可为实际多视点系统的建立提供理论依据。本文余下部分的结构如下：第2节和第3节分别给出多视点立体系统从采集端到显示端的映射关系和多视点立体角度模型；第4节导出立体视角与视点数的关系；第5节和第6节分别是仿真实验分析和本文的结论。

2 基于平行摄像机阵列的多视点立体显示映射关系

多视点立体显示系统是由摄像机阵列和多视点立体显示器两部分组成。使用摄像机阵列同时地从不同位置拍摄真实物体，将获得的多视点图像信息在多视点立体显示器中合成为立体对并显示出立体图像。

图 1(a)为多视点立体显示系统中的摄像机阵列。设世界坐标系原点处在屏幕中心，XY平面与屏幕平面重合，摄像机阵列与XY平面平行，摄像机光心与世界坐标系Z轴平行，摄像机阵列中相邻摄像机间距相等。摄像机阵列X轴和Y轴上的间距为tx和ty，阵列中左上角第1个摄像机的坐标为(xc,yc,zc,1)，第(i,j)个摄像机坐标为Cij=(xij,yij,zij,wij)，则Cij可以表示为

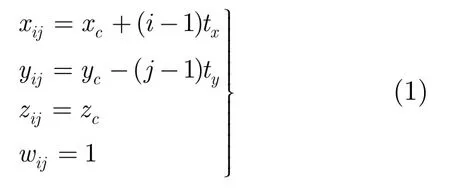
式(1)中，i=1,2,…,M,j=1,2,…,N,M和N为摄像机阵列的行与列，zc为摄像机平面与XY平面之间的距离。

图1(b)为人眼观看的多视点立体显示系统，为叙述方便这里以摄像机阵列中两个相邻摄像机拍摄到的立体图像来说明。假设VO是真实物体上的一点，Ccl和Ccr为拍摄真实点VO的摄像机阵列中的两个摄像机，他们分别拍摄到VO的立体像对在多视点立体显示器上显示为Sr和Sl。当第1个观察者的双眼处在VL1和VR1时，根据双目立体成像原理，可以观看到虚拟物体上的点处在Vl.1，以此类推，当第n个观察者双眼处在VLn和VRn时，观看到虚拟物体上的点为Vln。由上可见，多视点立体显示中不同位置的观看者能观看到虚拟物体的不同位置的立体图像。

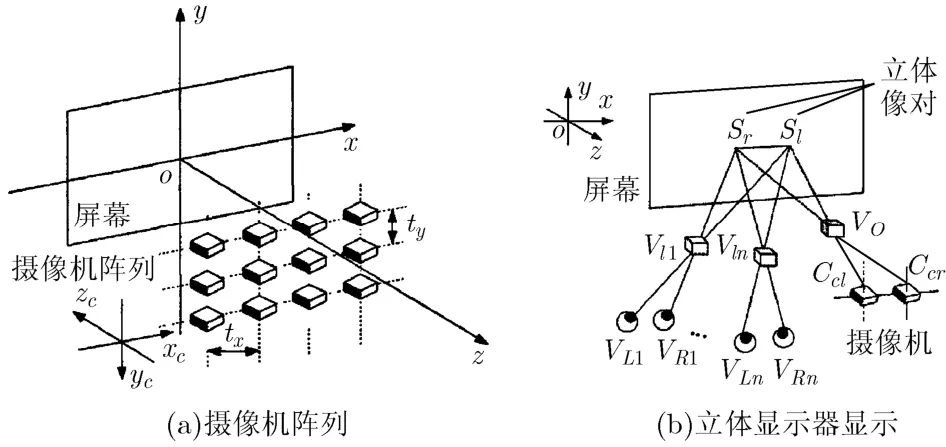
图1 多视点立体显示系统模型

3 多视点立体显示系统模型

根据上一节的分析，只有建立真实物体和虚拟物体之间的映射关系，才能更好地研究多视点立体显示系统，并且合理地调整参数，提高立体效果。

在多视点立体显示系统中，设真实物体上的一点为VO=(XO,YO,ZO,1)，观察者最终看到的虚拟物体上的对应点为VI=(XI,YI,ZI,1)，则真实物体与虚拟物体的对应关系可以用一个齐次矩阵M表示：

根据光学成像原理和计算机视觉双目视差原理[9]，从真实物体到虚拟物体总共经过了图2所示的4个坐标系转换过程。

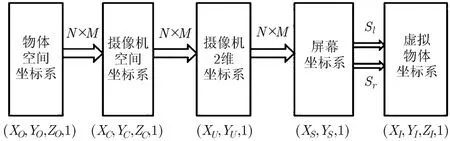
图2 多视点立体显示系统中坐标系转换过程

根据计算机视觉原理，由于摄像机位置、摄像机焦距和CCD放大倍数等情况的不同，第(i,j)个摄像机拍摄到的物体点的空间坐标VO=(XO,YO,ZO,1)转换到屏幕坐标Sij=(XS,YS,1)的映射关系可以表示为

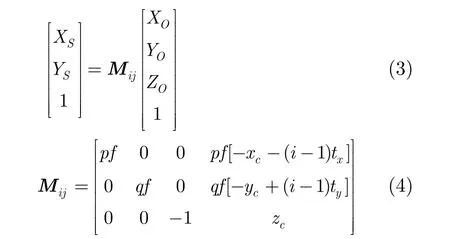
Mij是由第(i,j)个摄像机的位置Cij=(xij,yij,zij,wij)来决定的。摄像机焦距为f。从CCD到显示屏幕横向(纵向)的放大因子为p(q)，一般情况下，p=q。

根据双目成像原理[10]，真实物体被摄像机阵列中的一对摄像机拍摄后在屏幕上形成立体像对(XSl,YSl,1)和(XSr,YSr,1)。根据双目视差原理，立体像对从屏幕坐标系经过大脑融合转换到虚拟物体坐标系的立体图像点VI=(XI,YI,ZI,1)。

观看者的左眼和右眼的位置分别为VL=(XL,YL,ZL,WL)和VR=(XR,YR,ZR,WR)。左眼和右眼分别观看到屏幕上的像点为Sl=(XSl,YSl,1)和Sr=(XSr,YSr,1)。感受到的虚拟物体与屏幕上的立体像对之间的关系为

其中MR,ML分别为

把式(3)代入式(5)，就可以得到真实物体与虚拟物体之间的映射关系：

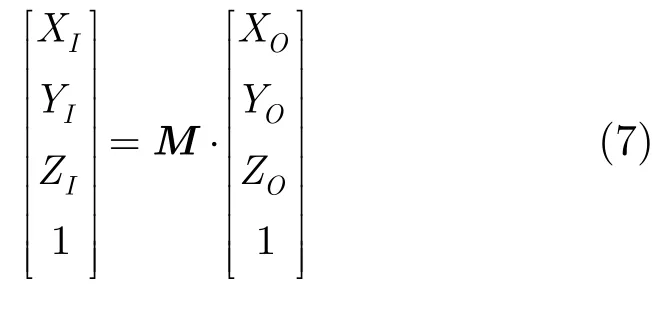
则M为

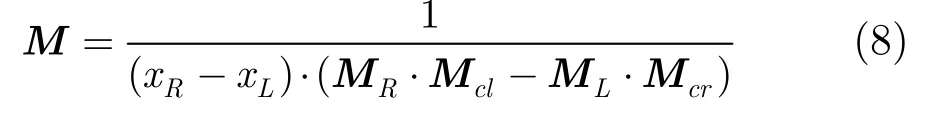
把式(4)，式(5)代入式(8)，可以得到

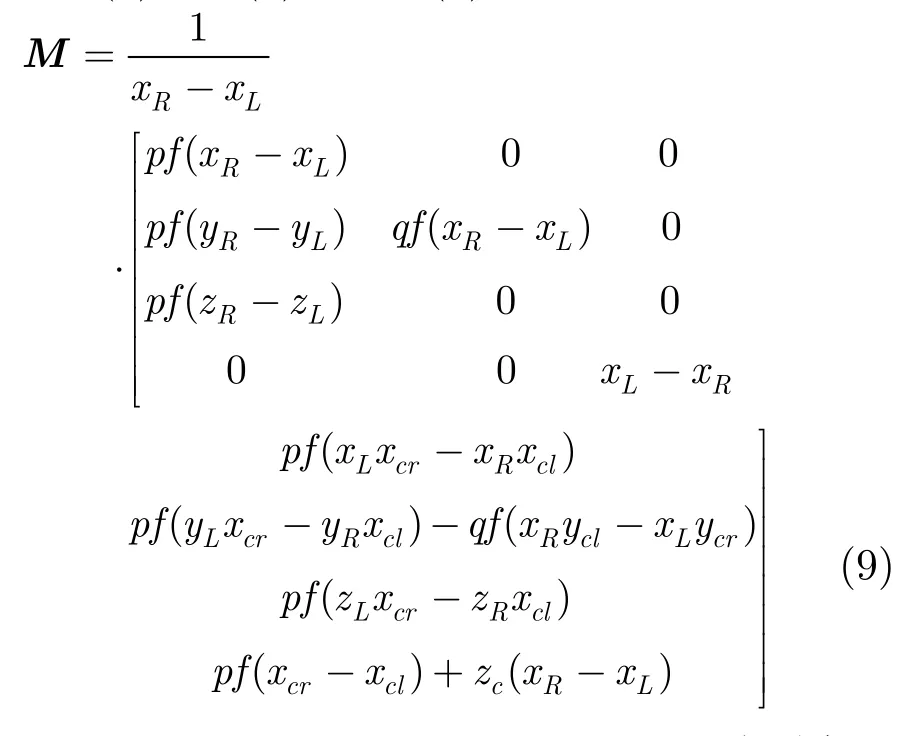
设Ccl=(xcl,ycl,zcl,1),Ccr=(xcr,ycr,zcr,1)分别表示拍摄真实物体时的左右摄像机坐标。由式(8)和式(9)可以得到人眼感受到的虚拟物体VI=(XI,YI,ZI,1)和真实物体VO=(XO,YO,ZO,1)之间的映射关系：

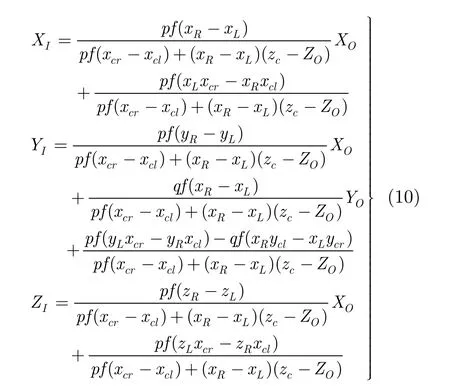
式(10)是多视点立体显示的数学模型，它包含拍摄时的摄像机阵列参数，可以此为依据预测立体显示图像的空间分布，优化实拍参数，得到更好的立体显示效果。

4 多视点立体视角模型

多视点立体视角是观看者在观看多视点立体显示器时，双眼与被观察物体之间所形成的角度。为了方便研究假设摄像机阵列为水平摄像机阵列，且相机间隔均匀，人双眼之间的距离为65 mm，人眼与立体显示屏幕平行，真实物体在观察者的正前方。

4.1 立体视角模型

设e为人双眼之间的间距，则e=xR-xL;a为水平摄像机阵列之间的距离，则a=xcr-xcl；人双眼与显示屏平行，则zL=zR=zv。由式(10)可知虚拟物体的深度ZI为

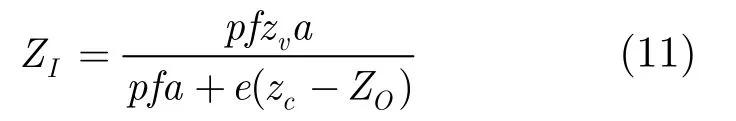
其中zv是观看者离多视点立体显示器的距离，zc为摄像机阵列到拍摄平面的距离，ZO为真实物体的深度。多视点立体角度2β是观察者的双眼与所形成的虚拟物体之间的夹角，根据式(11)和计算机视觉可得

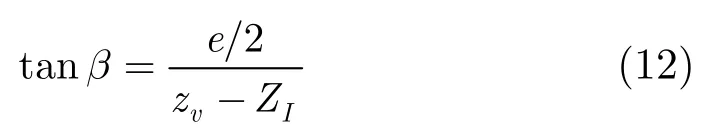
因此多视点立体视角模型为

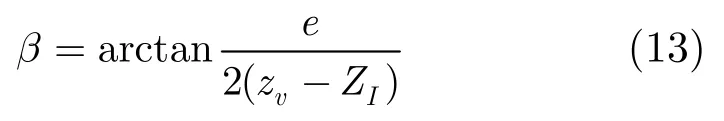
式(13)中β为多视点立体显示时双眼观察虚拟物体时的立体视角的半角(实际立体角度为2β，为方便叙述这里用β表示)，它与虚拟物体的深度ZI和观察距离zv存在定量关系。

4.2 人眼融合极限

对于人眼观看到的立体图像而言，视差(以H来表示)过大则人眼无法生成有效的虚拟物体，会产生重影或双轮廓。根据文献[11]的研究，人眼融合的极限H应满足：

根据双目立体显示原理，立体视角可以用视差来表示。

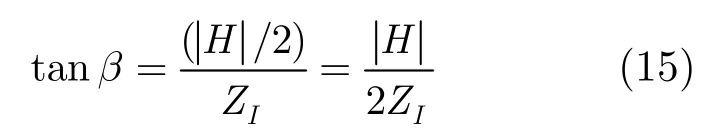
所以，

把式(16)代入式(14)，得

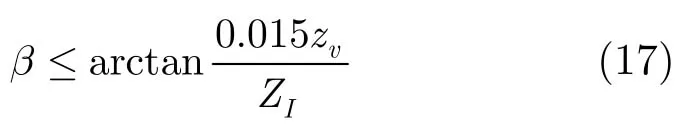
根据式(17)可知，立体角度受到人眼融合极限的制约。在实际拍摄时必须考虑人眼融合极限，否则会产生重影、双轮廓等现象影响立体观看效果。

4.3 立体角与视点数之间的关系

如图3所示，在理想情况下，对于平行摄像机阵列而言，观察物体上的某一点时，N个摄像机会产生N个相应的点，这N个点产生N-1对立体匹配对。根据裸视立体显示技术的原理，观察者通过在不同的位置观看这N-1个立体匹配对来生成可观察的虚拟立体点。可以观察到的最大立体视角Agmax即为这N-1个立体匹配点所生成的N-1个虚拟立体点的角度之和。

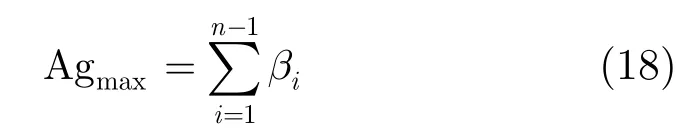
这里需要引入一个参数——视点切换参数，即产生视点切换时观察者平行移动的距离，此参数与观察者距离立体显示器远近有关。假定立体显示器为理想多视点立体显示器，即观察者在距离屏幕zv处水平移动时，视点切换参数为。与观察者观看距离有关，即当观察者在距离zv处观看裸视立体显示器时，每移动水平距离就造成视点切换，在下节的实验中取=32.5。如图3所示，对于N-1个视点，当观察者离显示屏的距离为zv时，从视点1过渡到视点N-1，需要水平移动(N-2)·。由此可得到裸视立体显示所能给出的最大立体角：

图3 多视点立体显示器的立体视角

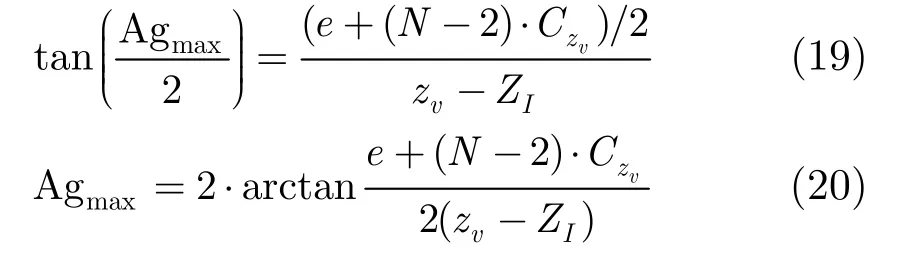
5 仿真实验结果和分析

5.1 制约立体视角的因素

在构建多视点立体显示系统时，必须要综合考虑摄像机阵列参数和观察者参数，才能得到最佳观看体验。表1中给出在1～6不同条件下进行仿真实验的多视点拍摄和观看参数，以验证式(13)得到立体角度与拍摄距离之间的关系。表1中p为放大因子，f为摄像头焦距，zv为观看距离，a为摄像机间距，ZO表示真实物体的实际深度。仿真实验中立体视角的单位均为弧度。

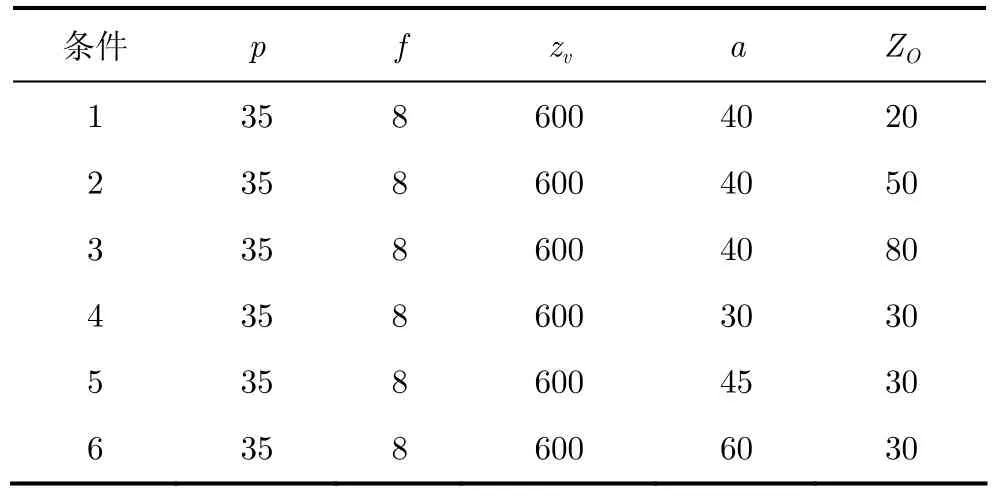
表1 摄像机阵列拍摄和观察参数(mm)

图4为在条件1，条件2，条件3时，实验所得的立体角与拍摄距离之间的关系。从图中可以看出随着拍摄距离的增加，立体角度也随之减少。对比条件1，条件2，条件3，还可以看出随着ZO增大，立体角度逐渐增大，当拍摄距离也增加时，立体角度趋于一致。图5为在条件4，条件5，条件6时，立体角度与拍摄距离之间的关系。对比条件4，条件5，条件6可以看出随着摄像机之间的间距a的增大，立体角度也逐渐增大，当拍摄距离也随之增加时，立体角度趋于一致。

可见立体角度受到拍摄距离、物体的真实深度和摄像机间距的影响，当物体真实深度或摄像机间距增加，会使立体角度变大，但当拍摄距离逐渐增加时，立体角趋向于恒定值。因此，在建立实拍多视点立体采集/显示系统时，必须要考虑拍摄场景中真实物体的深度范围和拍摄相机阵列之间间距。

5.2 人眼融合极限对立体角度的制约

如前所述，式(13)所示的立体角不能无限制地增大，它受到考虑了人眼融合极限后的式(17)制约。为便于说明这两者之间的关系，将表1中的实验参数取为表2。

表2 摄像机阵列拍摄和观察参数(mm)

图6-图9为实验所得的人眼融合极限与立体角度的关系，实线为立体角度与拍摄距离的关系，虚线为人眼融合极限，即虚线之下的区域(包括虚线)为理想观察区域，即处在该区域内的点能够观察到理想的立体效果。可以看出上述各图中，立体角度与人眼融合极限存在一个交叉点Q,Q右侧的点满足人眼融合极限，为理想观看区域可以优质地正常观看，而Q左侧的点形成的立体角度过大，无法形成可正常观看的立体效果，也即会产生重影和双轮廓等劣质图像。

5.3 视点数N与立体角度之间的关系

随着视点数的增加可以观看的立体角度也随之增大，而且虚拟物体的立体感增强。实验所用的参数如表 3所示，下面实验验证式(20)的视点数与立体角度之间的关系。

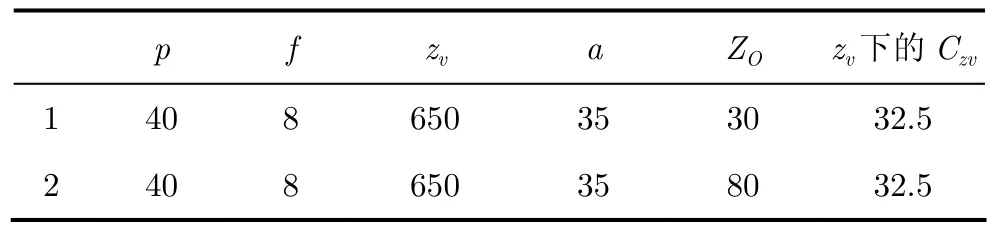
表3 摄像机阵列拍摄和观察参数(mm)

图10和图11中，立体角的单位为rad。从图中可以看出随着视点数的增加，立体角逐渐增大，但立体角度的增加幅度越来越少。对于水平摄像机阵列而言，立体角的极限为π(180°)。随着视点数的增加，立体角的增速在放缓，立体效果增强不明显；同时视点数的增加意味着所有摄像机的公共部分在减少，这说明所观察到的立体场景变小；而且由于摄像机价格、摄像机间距以及摄像机机身宽度等硬件因素的制约都使得视点数不能够无限增加。

图4 条件1，条件2，条件3时拍摄距离与立体角度之间的关系

图5 条件4，条件5，条件6时拍摄 距离与立体角度之间的关系

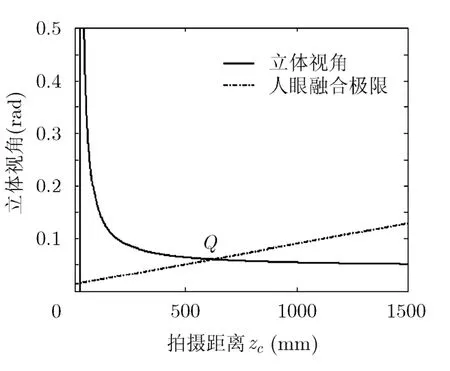
图6 条件1时拍摄距离与立体角度之间的关系

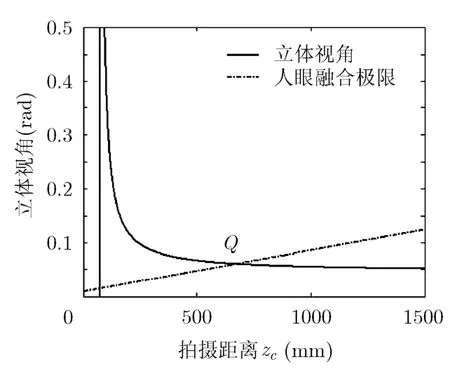
图7 条件2时拍摄距离与立体角度之间的关系

图8 条件3时拍摄距离与立体角度之间的关系

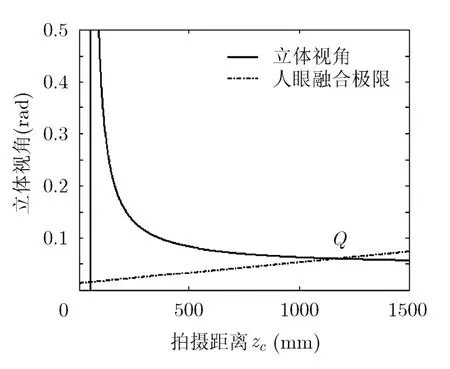
图9 条件4时拍摄距离与立体角度之间的关系

图10 条件1时视点数与立体角之间的关系

图11 条件2时视点数与立体角之间的关系

由上可见，在建立实拍多视采集/立体显示系统时，必须考虑摄像机阵列与拍摄场景之间的关系，通过调整摄像机阵列的位置、间距以及场景中各个物体的位置，使得观众在观看整个场景时场景内的所有点都处于人眼融合极限内。增加视点数虽可获得更大的立体观察角度、增强其立体感，但受到如前所述的限制，只能适量增加。

6 结束语

本文建立了多视点立体角模型，获得了拍摄距离与立体角之间的制约关系，通过仿真实验分析出摄像机间距与真实物体位置对立体角的影响。根据人眼融合极限，求出多视点系统拍摄时的最小拍摄距离和理想观看区域。并且得到视点数N与立体角之间的关系图，从图中可以看出，随着视点数的增加，多视点立体显示所能观察的最大立体角也相应增大，但视点数增加到一定数量时，最大立体角度的增幅趋饱和。所以在实际建立多视点立体显示系统时，不能盲目提高视点数来提升立体效果，而应综合考虑各方面的因素来优化多视点系统的立体效果。

[1]Zhang Zhao-yang, An Ping, Zhang Zhi-jiang,et al.. 2D/3D Video Processing and Stereo Display Technology[M]. Beijing:Science Press, 2010: 1-10.

[2]Tanimoto M and Wildeboer M. Frameworks for FTV coding[C]. IEEE International Conference on Multimedia and Expo, Japan, July 2009: 1552-1553.

[3]Lee C, Song H, Choi B,et al.. 3D scene capturing using stereoscopic cameras and a time-of-flight camera[J].IEEE Transactions on Consumer Electronics,2011, 57(3): 1370-1376.

[4]Kang Yun-Suk and Ho Yo-sung. Disparity map generation for color image using TOF depth camera[C]. The True Vision-Capture, Transmission and Display of 3D Video(3DTVCON), South Korea, May 2011: 1-4.

[5]Smolic A, Kauff P, Knorr S,et al.. Three-dimensional video postproduction and processing[J].Proceedings of the IEEE,2011, 99(4): 607-625.

[6]Shen Li-quan, Liu Zhi, An Ping,et al.. Low-complexity mode decision for MVC[J].IEEE Transactions on Circuits and Systems for Video Technology, 2011, 21(6): 837-843.

[7]Son J Y, Saveljev V V, Kim J S,et al.. Multiview image acquisition and projection[J].Journal of Display Technology,2006, 2(4): 359-363.

[8]Bi Jia-yu, Zeng Dan, Zhang Zhijiang,et al.. Automultiscopic 3D displays system model and evaluation[C]. World Congress on Computer Science and Information Engineering, China,March 2009, 6: 514-518.

[9]Forsyth D A and Ponce J. Computer Vision: A Modern Approach[M]. NJ: Prentice Hall, 2003: 3-19.

[10]Son J Y, Javidi B, and Kwack K D. Methods for displaying three-dimensional images[J].Proceedings of the IEEE, 2006,94(3): 502-523.

[11]Lipton L. Foundations of the Stereoscopic Cinema ——A Study in Depth[M]. NY: Van Nostrand Reinhold, 1982:91-118.