非合作水声脉冲信号的单水听器匹配场定位研究
2012-07-25方世良
李 焜 方世良 安 良
(东南大学水声信号处理教育部重点实验室 南京 210096)
1 引言
对水下目标实施定位是水声学中的一个热点问题。考虑到水声环境的复杂性,为了能够更准确地对水下目标实施定位,多数文献从声传播的角度出发,使用匹配场定位技术来确定声源的位置[1-5]。传统的匹配场定位技术,一般多采用阵列的处理方式,具有大的孔径,以获得良好的阵增益和分辨性能。但是采用多阵元的大阵列,一方面增加了系统的开销,给基阵的设计带来不便;另一方面,在实际海水中布放时会受到诸如阵倾斜以及阵元失效等问题,增加了对水下目标定位的难度。因此,研究只利用单个水听器来对目标进行定位一直被研究人员所关注,不断激励着相关研究人员为此进行探索。
在这方面,文献[6]将范数的不同表达式引入匹配场定位函数中,研究利用单水听器进行定位;文献[7]针对宽带信号提出了基于射线追踪模型的单水听器定位方法;文献[8]针对超低频信号采用模式滤波的方法来实现单个水听器的声源定位;文献[9]利用单水听器采用直方图滤波的方法对浅海中的移动目标进行定位;文献[10]讨论了在合作方式下借助波导不变量的性质来对目标实施定位;文献[11]研究了最小二乘的单水听器定位方法;文献[12]研究了利用单水听器对海洋生物实施定位的方法。
使用单水听器进行定位的一个难点在于可利用的信息量太少,主要是空间信息的缺乏。大多数文献借助宽带信号的多频点特性,从假设发射信号为已知的情形出发,采用“频点换孔径”的思想,对宽带目标信号实施定位。此种方法需要进行多频点合成,频点数越多,估计效果越精确,但同时计算量较大。对于非合作类的水声脉冲信号而言,其在时间上具有瞬时性,带宽上具有窄带性,且所能获得的发射信号的先验信息有限,因此若对该类信号实施被动定位,由于信号的频率,波形等信息未知,从而进一步地增加了对该类水声脉冲信号定位的难度。
因此,利用单水听器对非合作水声信号进行定位之前,首先需要对水听器接收信号的参数进行预估,获得目标发射信号的频率,这是进行后续定位工作的前提。由于目标信号的频率未知,若直接采用傅里叶变换的方法在全频率段内进行频率搜索,则计算量较大,且受工作频段的限制,存在频点遗漏的情形,会造成频率估计的偏差较大。同时此种方法仅在单一域内进行,不能反映水声脉冲信号的局部特征。考虑到水声脉冲信号具有短时瞬态的非平稳特性,常采用时频分析的方法来进行参数估计。但是,传统的基于固定核函数的时频分析方法,如Wigner-Ville分布、Choi-Williams分布等,只适应于某种特定的信号,存在时频分辨力低和交叉项干扰等问题,导致参数估计的效果下降。针对这一不足,Baraniuk等人[13]提出了基于信号的自适应径向高斯核函数(ARGK)的时频分析方法,其核函数的形状根据所分析的信号自适应地变化,提高了对于非平稳信号参数估计的性能。之后,文献[14]对这一方法进行了推广,提出了基于信号的自适应核函数的广义形式。
本文针对非合作的水声脉冲信号,研究利用单水听器的匹配场定位。总体思路是通过设计基于自适应径向高斯核函数的时频分布进行参数估计,获得目标信号的频率,使用时域最小二乘的方法进行单水听器匹配场定位。利用非合作水声脉冲信号的窄带特性以及瞬时非平稳特点,讨论了自适应径向高斯核函数时频分布的设计方法和参数估计的效果,分析了基于最小二乘的单水听器估计方法的性能,通过仿真验证和对实际海试数据的处理,说明了该文方法的有效性。
2 信号模型
位于海洋环境中(r0,z0)位置处的发射信号经过海洋波导传播后,单一接收水听器所接收到的信号可以表示为如下卷积的形式:
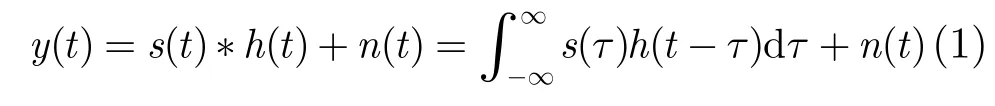
其中s(t)为发射信号,h(t)为海洋信道脉冲响应,n(t)为噪声。
在离散时间情形下,可将式(1)表示为时域卷积和的形式:

将式(2)写为矩阵运算形式,则有

其中
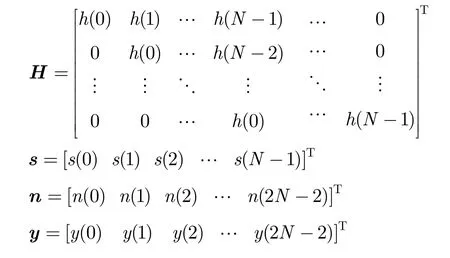
3 基于信号的自适应高斯核函数时频分布
设计具有自适应径向高斯核函数的时频分布对单水听器接收信号的频率进行估计时,先求解接收信号在2维频偏-时延域上的模糊函数,
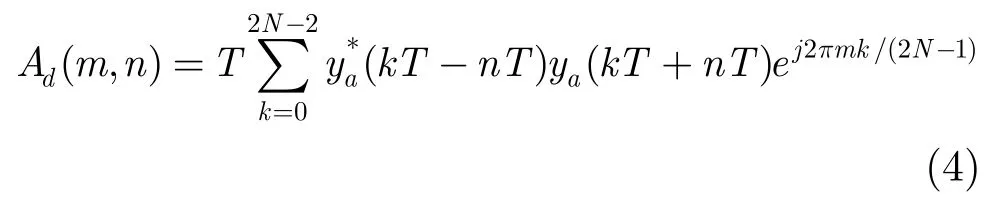
其中T表示采样时间间隔,ya表示接收信号经Hilbert变换后的解析信号。
Baraniuk[13]指出满足自适应核函数设计所要求的函数为 2维频偏-时延(θ-τ)域上的径向高斯核函数。

其中ψ=arctan(τ/θ)为径向与水平方向的夹角,σ(ψ)称为扩展函数,它控制径向高斯核函数在ψ方向的扩展。

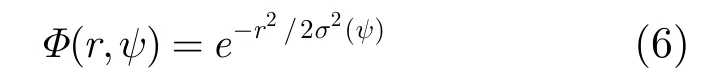
设计与信号有关的自适应核函数等同于求解具有最优的径向高斯核函数。由式(6)可知,2维径向高斯核函数的形状完全取决于 1维的扩展函数σ(ψ)。在离散情形下,求解最优的径向高斯核函数可通过求解如下的最优扩展函数来得到

其中
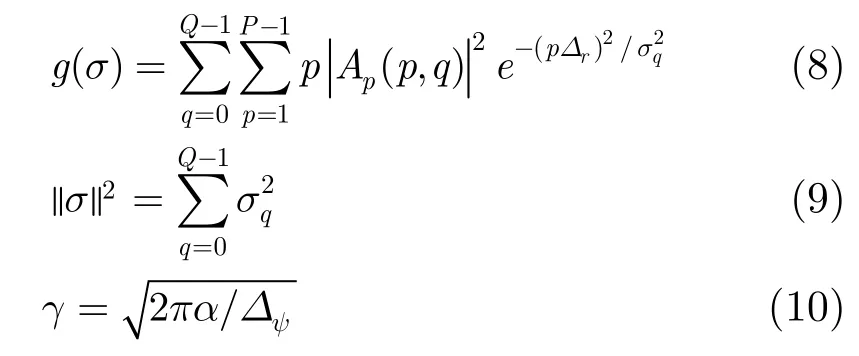
式中σq=σ(qΔψ),Ap(p,q)分别为离散化的扩展函数和极坐标系下的模糊函数,p=0,1,…,P-1,q=0,1,…,Q-1为离散化的r,ψ所取的点数,Δr,Δψ为相应的采样间隔,α为最优核体积参数,取值范围一般为1~5。
对于式(7)的优化问题,可采用变步长的梯度上升算法来进行求解,设定初始值为
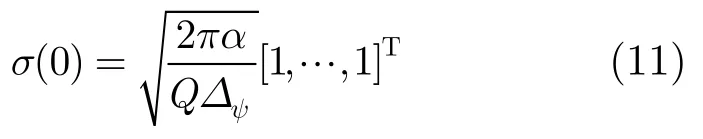
迭代

并对每次迭代后的σ(k)进行如下的归一化处理:

为减小计算量,对每次迭代所选取的步长,采用非精确的1维搜索Goldstein-Armijo准则[15]进行约束限定。求出扩展函数后就可得到离散频偏-时延域下最优的径向高斯核函数:
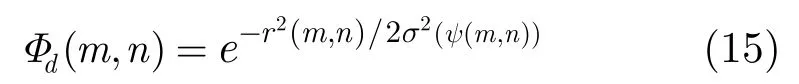
将求出的最优高斯核函数与模糊函数的乘积进行2维傅里叶变换,即可得到自适应高斯核函数的时频表示。
4 定位原理
在阐述基于最小二乘的单水听器定位原理之前,本部分首先给出如下的两个定理,它们是此方法的理论基础。
定理1信道脉冲响应所构成的卷积矩阵H为列满秩矩阵,其秩为N,且存在唯一的广义逆为
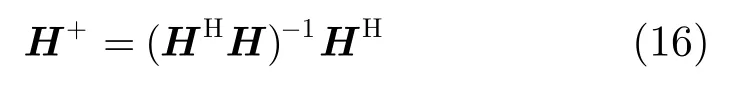
定理2卷积矩阵H和它的广义逆H+的乘积不等于单位阵,即

由式(3)的数学表达式可以看出,水听器接收到的信号可以表示成信道脉冲响应所构成的卷积矩阵H和发射信号s的乘积,再叠加上噪声n。在获知某海洋环境参数(如声速剖面、海水深度、地声参数)的条件下,对感兴趣的海洋区域,可将声场按照距离r和深度z划分成有限个网格点,通过声场传播模型计算出每个网格点位置上声源激励所产生的信道脉冲响应,得到不同距离和深度上的卷积矩阵(r,z)。若已知发射信号,则将发射信号与信道脉冲响应进行时域卷积,就可以得到用于匹配场计算时的拷贝场信号。而在非合作条件下,由于发射信号未知,无法直接得到拷贝场信号,因此在获知信号频率的基础上,需要借助仅有的单水听器接收信号和计算出的海洋信道卷积矩阵对搜索区域每个网格点上的发射信号进行估计。
利用最小二乘的方法构造如下的误差函数:
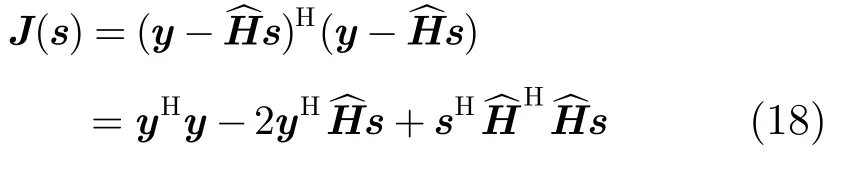
对式(18)中s进行求导,并令导数为0,就可以得到每个网格点上发射信号的估计值。
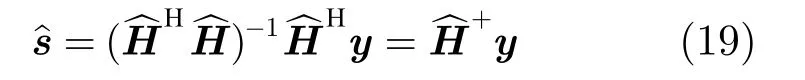
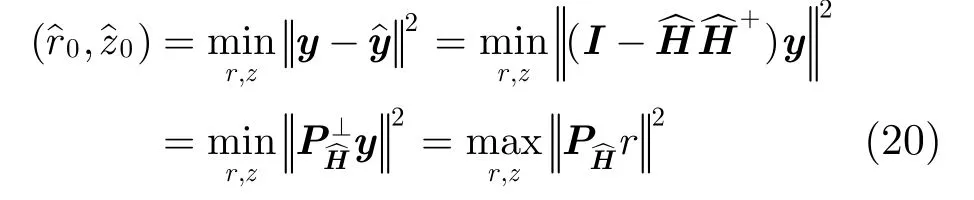
其中表示的投影阵,为其正交补投影阵,为目标真实位置(r0,z0)的估计值。
由上面所给出的定理1和定理2可知,定理1卷积矩阵及其广义逆的惟一性保证了对于不同的声源位置具有不同的信道脉冲响应,从而保证了定位结果的惟一性;而定理2则说明,单水听器的匹配场定位需要利用信道卷积矩阵和水听器所接收到的信号。由于信号频率未知,采用自适应径向高斯核函数的时频分布进行频率预估,将估计出的频率值作为前向声场模型计算所需要的频率。在后续定位过程中,利用单水听器采用时域最小二乘的方法来得到搜索网格区域上的拷贝场信号。在不计入噪声影响时,令表示通过频率估计后所计算得到的信道卷积矩阵,则相应的误差函数可以表示为

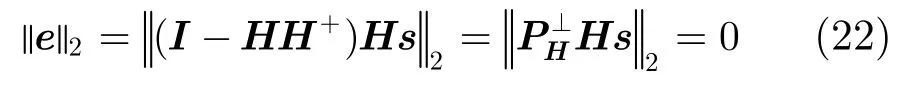
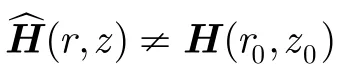
5 仿真实验与海试数据处理
5.1 数值仿真
脉冲信号类型选为线性调频信号,频带范围为100~200 Hz,脉冲宽度为0.05 s。源深度为60 m,接收水听器深度为80 m,源与接收机之间的距离为5 km。海洋环境参数为:海水深度为110 m,海水密度为ρw=1.0 g/cm3,声速剖面如图 1(a)所示,海底密度ρb=1.9 g/cm3,海底声速cb=1 700 m/s ,衰减系数为0.5 dB/λ。模拟水听器上的接收信号为声源位置处的信号在接收水听器上的响应,并叠加高斯白噪声,SNR=10 dB,水听器上的接收信号如图1(b)所示。
实验1信号频率对单水听器匹配场定位的影响 在对信号频率进行估计时,由于受工作频段的限制,存在频点遗漏的情形,从而产生估计误差。为说明这一点,以频率估计误差分别为2 Hz, 5 Hz以及 10 Hz,仿真在不同信噪比条件下,频率估计误差对于单水听器匹配场定位精度的影响。图2为3种频偏下单水听器定位模糊表面输出的相关峰值以及定位误差。
由结果可以看出,单水听器匹配场的定位性能随频率估计误差的增大而下降;当频率估计的误差较大时,定位输出的结果与目标真实位置之间的误差不再随着SNR的增加而减小,即使当信噪比很高时,仍不能实现精确定位。因此,需要对信号的频率进行精确估计。
实验2最优核函数时频分布的参数估计效果 设计最优径向高斯核函数的时频分布对接收信号进行参数估计,图 3(a)给出了相应的时频分布结果。由时频分布图可以看出,采用自适应的径向高斯核函数所得到的结果在时频分布图上具有很好的时频聚集性,且很好地抑制掉了由于多途产生的各分量之间的交叉项。对时频分布的结果进行峰值搜索,求得峰值位置处瞬时时刻沿频率方向的切片图,如图3(b)所示。由图可以看出,频率波形较为尖锐,所估计出的接收信号的中心频率为149.6 Hz,接近真实中心频率。
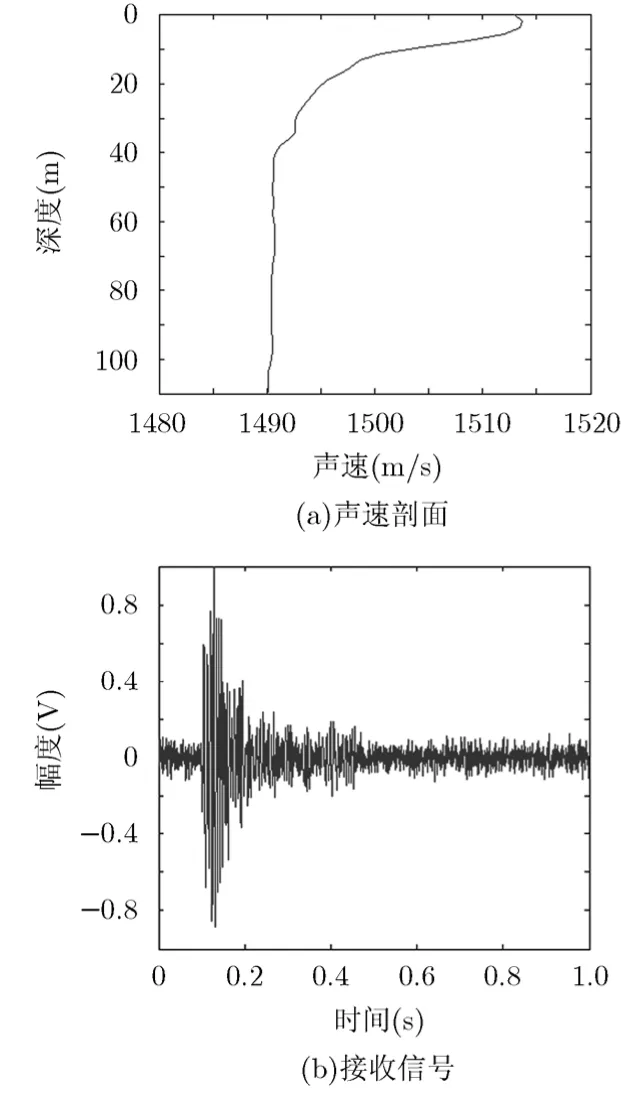
图1 仿真所用的声速剖面和单水听器上的接收信号
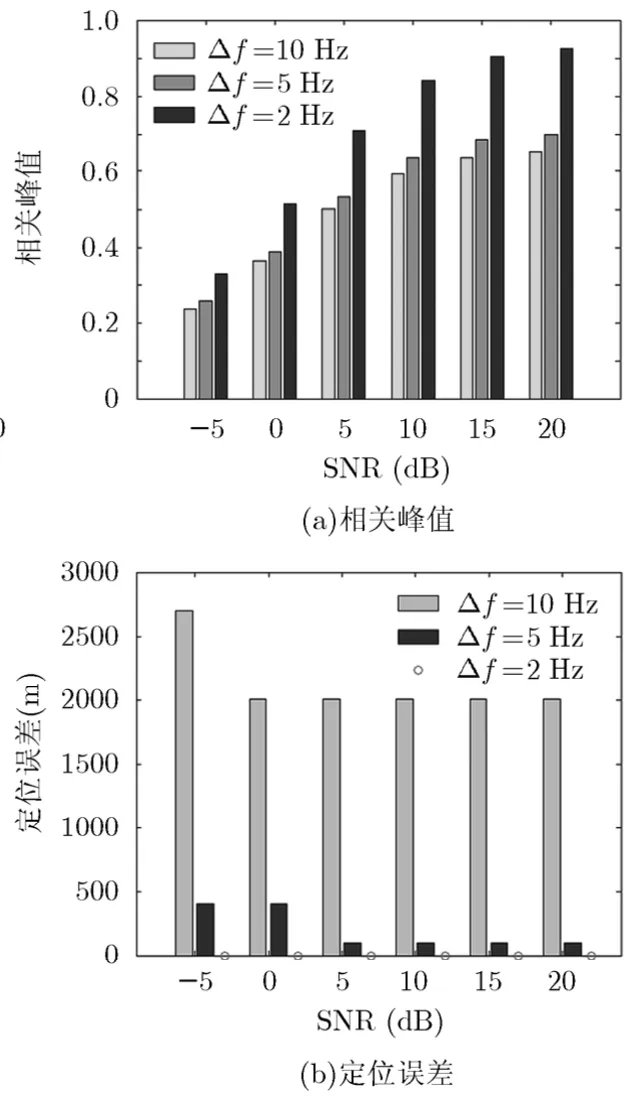
图2 不同信噪比下频率估计误差对单水听器匹配场定位的影响
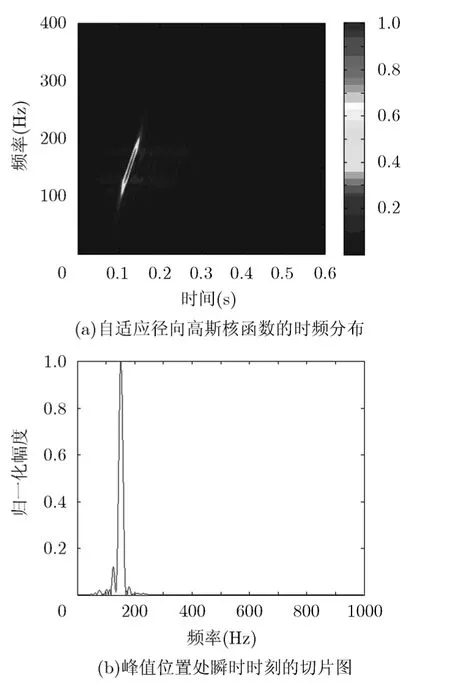
图3 自适应高斯核函数参数估计结果
实验3单水听器定位结果分析 在获得信号频率的基础上,采用基于最小二乘的方法进行单水听器匹配场定位。声源搜索范围为距离2~7 km,步距100 m,深度5~105 m,步距2.5 m,本文方法求得的定位模糊表面结果如图 4(a)所示。为了进行对比,对文献[6]的方法进行了仿真,相应的定位模糊表面如图4(b)所示。由结果可以看出,文献[6]方法所给出的定位结果与目标实际位置有所偏差,此种通过测量源信号频谱的平坦性来确定目标位置的方法,只有当声源信号的频谱幅度较平坦时,才能很好地工作。而本方法所给出的定位结果正确地反映了目标所在位置,模糊表面的峰值较为清晰。
实验4环境不确定问题的讨论 此实验分析由于海洋环境的不确定性对于定位结果的影响。在以上所给出的环境参数的基础上,使海水深度和底部衰减系分别在 105~115 m 的范围内和 0~0.8 dB/λ的范围内均匀变化。对每种情形下的不确定性采用正确定位概率和输出峰值背景比来进行表征。正确定位概率以定位输出结果距真实距离为±500 m,深度为±10 m以内时的定位次数。峰值背景比定义为在定位正确的前提下,模糊表面的输出峰值与正确定位区间之外模糊表面输出的平均值之比。图5分别给出了在不同信噪比条件下正确定位的概率和输出峰值背景比。
由仿真结果可以看出,随着信噪比的提高,环境不确定性对定位所造成的影响减弱,在高信噪比条件下,正确定位的概率达到0.8,峰值背景比输出接近11 dB。
5.2 海试数据处理
为了检验本方法在实际中的性能,对某海试实验的数据进行处理,实验海区的声速剖面如图6所示,海水深度为55.5 m,海底声速为1650 m/s,海底密度 1.9 g/c m3,衰减系数为0.5 dB/λ。由于受到海水温度、盐度和深度的作用,此海洋信道中,存在不均匀的声速分布,会使声波发生折射,同时受海面和海底反射的影响,从而产生多途的信道结构。接收水听器位于水下30 m,发射信号采用大功率甚低频声源,脉冲长度为1 ,频率范围为70~90 Hz的线性调频信号,深度为11 m,距离水听器为3 km。图7分别给出了自适应径向高斯核函数的时频分布、瞬时频率估计以及中心频率估计结果。由结果可以看出,使用自适应高斯核函数时频分布具有很好的时频聚集性,所估计出的信号中心频率为79.9 Hz,与实际中心频率基本吻合。
对此目标信号按深度搜索步距为1 m,距离搜索步距为50 m进行单水听器匹配场定位,相应的模糊表面如图8所示。实验结果深度估计为8 m,距离估计为3.1 km,定位结果与目标源的真实位置基本符合,说明本方法具有一定的效果。

图4 单水听器匹配场定位结果
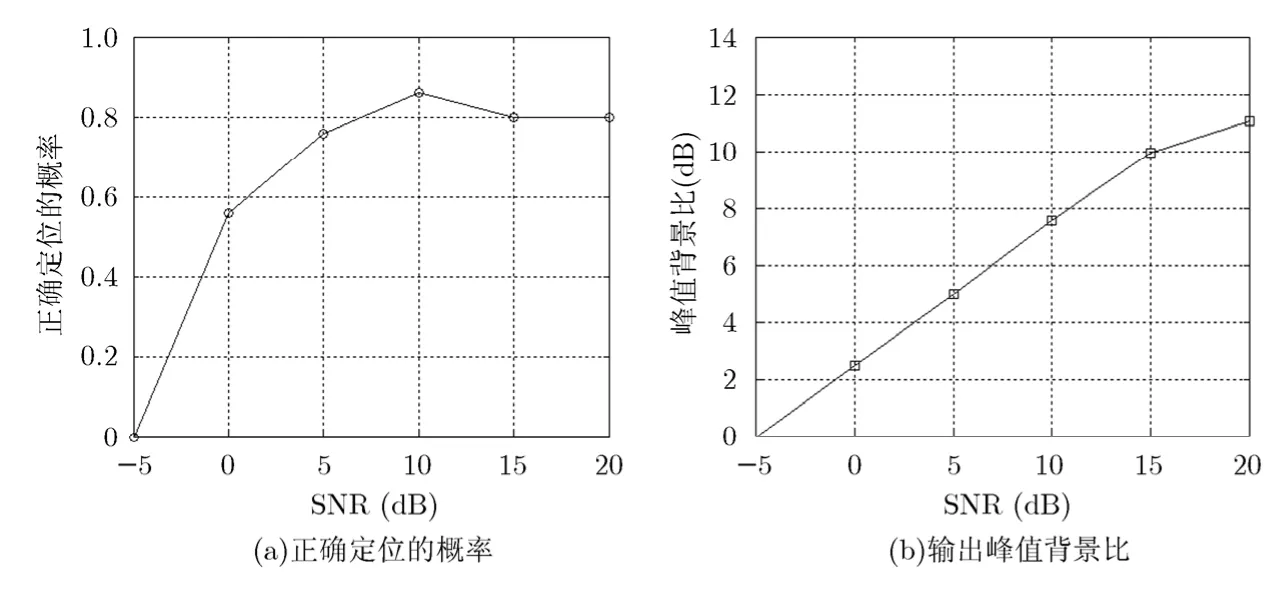
图5 不确定环境条件下定位算法的性能曲线

图6 实验海区的声速剖面
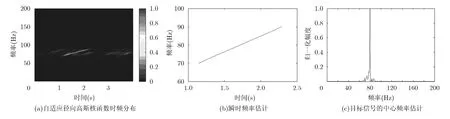
图7 自适应径向高斯核函数的频率估计结果
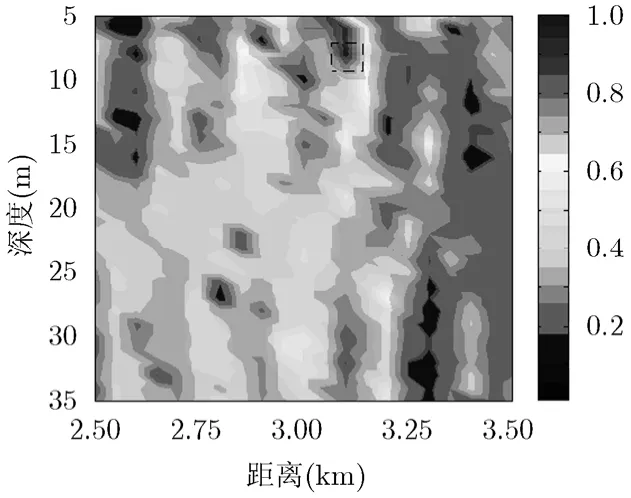
图8 定位模糊表面
6 结束语
使用单水听器来对水下目标定位一直是国内外研究的热点和难点。本文以非合作水声脉冲信号作为对象,研究非合作条件下的单水听器匹配场定位。设计具有自适应径向高斯核函数的时频分布获得目标信号的频率参数,利用时域最小二乘的方法,借助信道卷积矩阵的广义逆性质,建立拷贝场信号与接收信号之间的误差函数,获得目标信号的位置。采用最优径向核函数的时频分布可根据信号本身的特点自适应的变化,对信号的形式无特定的要求;通过最小二乘的方法进行匹配场定位,无需已知发射信号的波形及其它相关参数,体现了算法本身对于信号参数较低的依赖性。通过对窄带脉冲信号进行数值仿真和海试数据的验证,结果表明,自适应径向高斯核函数的时频分布具有良好的时频聚集性和抑制交叉项的能力,频率估计接近目标真实频率;匹配场定位模糊表面具有较为清晰的峰值,估计结果甚为准确。
[1]Lin W S, Liang G L, Wang Y,et al.. Source localization with acoustic intensity flux matched-field processing[C]. 2011 International Conference on Wireless Communications and Signal Processing(WCSP), Nanjing, November 2011: 1-4.
[2]Xu W, Xiao Z, and Yu L. Performance analysis of matchedfield source localization under spatially correlated noise field[J].IEEE Journal of Ocean Engineering, 2011, 36(2):273-284.
[3]Wu K M, Ling Q, and Wu L X. Positioning ability comparison research on several matched-field processing methods with increasing white noise[C]. 2011 IEEE International Conference on Signal Processing,Communications and Computing(ICSPCC), Xi,an,September 2011: 1-5.
[4]Kim K, Seong W, and Lee K. Adaptive surface interference suppression for matched-mode source localization[J].IEEE Journal of Ocean Engineering, 2010, 35(1): 120-130.
[5]Wang Q and Jiang Q. Simulation of matched field processing localization based on empirical mode decomposition and Karhunen-Loeve expansion in underwater waveguide environment[J].EURASIP Journal on Advances in Signal Processing, 2010, Article ID 483524, 1-7.
[6]Frazer L N and Pecholcs P I. Single-hydrophone localization[J].Journal of Acoustical Society of America, 1990, 88(2):995-1002.
[7]Jesus S M, Porter M B, Stephan Y,et al.. Single hydrophone source localization[J].IEEE Journal of Ocean Engineering,2000, 25(3): 337-346.
[8]Touze G L, Torras J, Nicolas B,et al.. Source localization on a single hydrophone[C]. IEEE Oceans’2008, Quebec City,September 2008: 1-6.
[9]Jemmott C W, Culver R L, and Bose N K. Passive sonar target localization using a histogram filter with modelderived priors[C]. IEEE Conference on Signal, Systems and Computers, Asilomar, October 2008: 283-287.
[10]Tao H L, Hickman G, Krolik J L,et al.. Single hydrophone passive localization of transiting acoustic sources[C]. IEEE Oceans’ 2007, Aberdeen, June 2007: 1-3.
[11]Chapin S R. Application of the method of least squares to a solution of the matched field localization problem with a single hydrophone[D]. [Ph.D. dissertation], The University of New Orleans, 2008.
[12]Tiemann C O, Thode A M, Straley J,et al.. Three-dimension localization of sperm whales using a single hydrophone[J].Journal of Acoustical Society of America, 2006, 120(4):2355-2365.
[13]Baraniuk R G and Jones D L. A signal-dependent time-frequency representation: optimal kernel design[J].IEEE Transactions on Signal Processing, 1993, 41(4):1589-1602.
[14]Honeine P and Richard C. Signal-dependent time-frequency representations for classification using a radially Gaussian kernel and the alignment criterion[C]. 2007 IEEE/SP 14th Workshop on Statistical Signal Processing(SSP’07),Madison,August 2007: 735-739.
[15]Cohen A I. Stepsize analysis for descent methods [J].Journal of Optimization Theory and Applications, 1981, 33(2):187-205.
