基于偏振分析的瞬态干扰抑制方法
2012-07-25朴胜春祝捍皓
刘 伟 朴胜春 祝捍皓
(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)
1 引言
矢量水听器可以同步共点测量声场标量和矢量信息,为后置信号处理提供更多的信息。它的诸多优点使其一经出现,便受到了国内外学者的普遍关注,已广泛应用于海洋开发及研究中[1,2]。通常情况下,实验海区并非安静海域,渔民作业、过往船只和天气等因素都会导致接收信号中不可避免地存在一些瞬态干扰。这类干扰具有持续时间短、强度高和频带宽的特点,直接影响信号处理的性能,因此必须对瞬态干扰进行抑制。
目前在雷达信号处理中已有很多方法可以抑制瞬态干扰[3-8],文献[3]利用复数据经验模式分解实现瞬态干扰的检测、抑制和数据重构。文献[4-7]都是先找到瞬态干扰位置,将瞬态干扰去除,再利用文献[8]中所描述的线性预测方法恢复信号。文献[4]利用分形检测,提取信号的相似性特征,找到瞬态干扰位置;文献[5]利用高分辨算法TLS-ESPRIT检测干扰发生位置;文献[6]应用信号子空间检测, 实时判决信号的奇异值,找到干扰位置;文献[7]利用线性预测AR模型递归最小二乘(RLS)求解零点后聚类估计瞬态干扰的位置。这些方法均是针对雷达信号特点而提出的,算法相对较复杂。
本文利用矢量水听器的特点,提出一种新的瞬态干扰消除方法。首先对接收的矢量信号进行偏振特性分析,获得偏振参数;再根据信号和瞬态干扰在偏振状态上区别,设计极化滤波器,对信号进行滤波,去除瞬态干扰;最后通过信号的偏振模型恢复瞬态干扰处数据。
2 矢量信号的偏振参数提取
偏振的概念最早起源于光学,现已广泛应用于地震学和电磁学等领域[9-12]。偏振分析又称极化分析,是矢量信号的共有属性,用于描述质点运动轨迹[12]。水中传播的声波为纵波,当入射信号中仅存在直达声时,接收信号的空间质点运动轨迹是直线;由于多途结构的存在,入射声波为多个同频平面波叠加,合成的振速矢量在此情况下是旋转矢量,因此,在流体和气体声场中,偏振的概念也成立,并可用偏振分析将椭圆的属性表示为定量值[2]。
将椭圆轨迹上样点看作一批空间点的集合,通过统计的方法获得椭圆的属性。偏振分析常用的方法为特征分解、奇异值分解和时频分析方法,本文采用特征分解方法。设t时刻接收矢量信号为S(t)=[vx(t)vy(t)vz(t)]T+N(t),T>t>0,N(t)是均值为0且功率为σ2的高斯白噪声。由此获得信号的协方差矩阵[13]
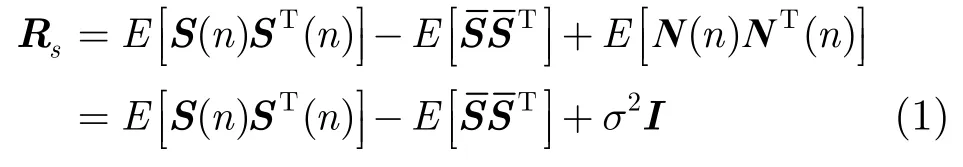

若信号为线性偏振,椭圆率可能无限大,故常用直线性描述信号偏振状态[13],即

时间窗长度的选择对偏振参数的获取产生一定影响。若时间窗过长,一个时间窗内存在几种偏振状态,偏振分析不能反映质点运动轨迹的真实情况;若时间窗长度过小,信号的统计特性变差,协方差矩阵易受噪声影响。时间窗长度的选择可采用“三次零点法”。将信号看作“+”,“0”,“-”组成的序列,一个时间窗内“0”最多出现 3次,“+”或“-”出现次数不受限制。若发射信号为单频信号,3个“0”符号即组成一个信号周期,文章中采用信号周期长度作为时间窗长度。
3 基于偏振分析的瞬态干扰抑制方法
3.1 信号模型
若信号中不存在噪声和瞬态干扰时,多途环境下目标信号可以化简为
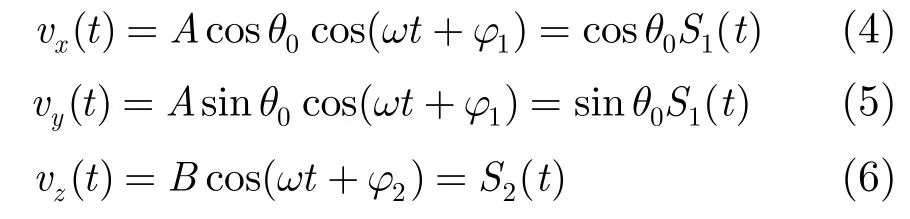
其 中S1(t)=ΣAkcosφkcos(ωt-ωτk),S2(t)=ΣAksinφkcos(ωt-ωτk),θ0为目标方位角,Ak,τk和φk为每个途径的幅度、时延、俯仰角及多途距离。通过推导可知,多途环境下,接收信号质点运动为具有固定偏振参数的椭圆。
实际接收信号中不仅存在目标信号,还混有噪声和瞬态干扰,即

式中i(t)为瞬态噪声。无瞬态干扰时质点运动轨迹为具有小抖动的椭圆,椭圆的主轴方向在小角度内摇摆。当瞬态干扰存在时,由于其具有高强度特点,目标信号被淹没,干扰占主导地位。由于瞬态干扰的偏振状态是杂乱无章的,质点偏离固定轨迹向随机方向运动。
3.2 瞬态干扰抑制
接收信号在未存在瞬态干扰和存在时,具有不同偏振状态。Flinn设计了极化滤波器,利用调制函数将具有某种特定偏振状态的信号保留,并减弱具有其他状态的信号。信号分离公式为[13]
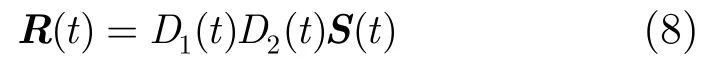
式中D1(t)为与椭圆反椭圆率有关的加权系数,D2(t)为与偏振方向有关的加权系数,S(t)为需要降噪的信号。D1(t),D2(t)共同作用,构成调制函数,实现滤波功能。Alkaz提出了将锥形高斯函数作为权值[12]
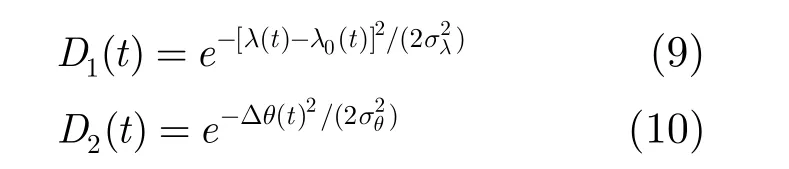
式中λ0(t)为期望的直线性,σλ为反椭圆率标准偏差,Δθ(t)是计算得到的偏振方向与期望的偏振方向之间的角度差,σθ为角度标准偏差。
理论上,最佳的期望直线性和角度为无瞬态干扰时信号的偏振参数,但由于不能确定瞬态干扰位置,实际上并未如此设置。考虑到瞬态干扰持续时间非常短的特点,受瞬态干扰影响的信号长度远小于无干扰信号长度,采用平均值作为公式的参数,可将瞬态干扰的影响降低。将期望的直线性和角度差设置为整段信号偏振参数的平均值,标准偏差为整段信号偏振参数的均方差。
从式(9)和式(10)中可看出,加权系数对偏振参数的变化具有一定的“容忍”区间,若偏振参数在此区间内,加权系数比较稳定,在0.9-1.0之间;若超出此区间,输出结果便会迅速减小,甚至会接近于0。瞬态干扰的存在,导致偏振参数不规则变化,且超过“容忍”区间,加权函数值急剧下降。利用式(8)进行极化滤波后,瞬态干扰处信号幅度会远小于无干扰处信号幅度,甚至接近于 0,实现瞬态干扰抑制。
从上述分析可知,当调制函数值急剧下降,瞬态干扰到达;调制函数值急剧上升时,已无瞬态干扰影响。对调制函数值设定门限,认为低于门限时存在瞬态干扰。噪声的存在,导致两个加权函数值在0.9-1.0间抖动。综合考虑两个加权函数,门限值应小于0.8,具体数值应根据不同情况分析。本文中以D1(t)D2(t)≤0.707作为干扰存在的判断依据,此点为半功率点,即信号功率下降为原来一半。
窄带信号具有明显的偏振特性,宽带信号则不尽然。由于传输介质的频散特性,不同频率声波传播速度不同,这种频散现象在低频段尤为明显。若分析信号包含频散特性明显的频率区域,不同频率成分到达时间有一定差别。此时,极化状态不稳定,随时间变化,需要将宽带信号看作多个窄带信号,对每段窄带信号单独处理,再合成宽带结果。对于频散特性不明显的接收信号,需要考虑两种不同情况:信号包络随时间剧烈变化和信号包络缓变(或基本不变)。对于前一种信号,同样需要将宽带信号看作多个窄带信号;后一种信号包络基本不变,且频散影响较小,比如线性调频信号,其椭圆轨迹比较固定,可以直接采用本文所提出方法进行瞬态干扰抑制。
3.3 数据恢复
当信号呈现某种特定偏振状态时,矢量信号可以由偏振参数表达
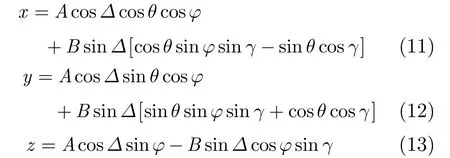
式中Δ为坐标点与原点连线方向和主轴方向夹角,A和B分别为偏振椭圆长短轴长度,θ为偏振方位角,φ为偏振俯仰角,γ为椭圆短轴方向与y轴夹角。上述参数中除Δ外均可由偏振分析获得,则获得Δ值便可对瞬态干扰处信号进行恢复。Δ值的估计方法有很多种,包括BP神经网络,AR模型预测和曲线拟合等。曲线多项式拟合方法适用于规律较简单的曲线,对于不满足多项式规律的曲线误差较大;BP神经网络为非线性预测方法,适用于已知样本点比较随机的情况;AR模型可以从已知样本点寻找规律,对某一时刻信号幅度进行预测。由于质点沿着固定的轨迹运动,夹角Δ值满足某一规律,为了更好地获得参数规律,本文中选择AR模型对参数进行预测。若已知{Δ(m-P),Δ(m-P+1),…,Δ(m-1)},则可以利用它们来预测m时刻值Δ(m)
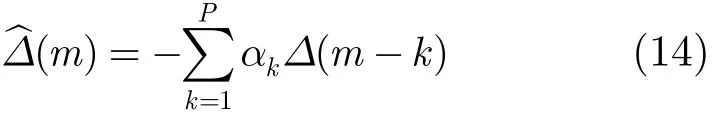
式中αk,k=1,…,P为AR模型参数。改进的协方差方法具有较好的估计性能,文中利用此方法确定AR模型参数值[14]。
4 处理结果分析
4.1 仿真结果分析
仿真环境:发射频率为400 Hz信号,目标方位角为50°,俯仰角为20°。无噪声和瞬态干扰的3维矢量信号可由几何关系得到,将3个振速分量分别记为vx,vy,vz,它们的功率为-7.3892 dB,-5.8655 dB和-12.3293 dB,噪声功率为-20 dB,在0.0501-0.053 s时间段内存在瞬态干扰。
为了将瞬态干扰去除,采用滑动窗方法分析信号的偏振特性。根据文中方法设计加权函数,构建极化滤波器,极化滤波器的加权函数见图1。从图1中可以看出,第1个加权函数的权值在0.05 s附近很小,在0-0.2范围内变化;理论上权值应该在0.05 s点上迅速下降,但从图中观察到,权值是逐渐下降的,由于采用滑动窗处理方法,相当于对输出结果进行了平滑处理;而其他时间段内权值在0.9-1.0范围内变化。
第 2个加权函数权值在 0.5s附近也较小,在0-0.9范围内变化;其他时间段内权值在0.9-1.0范围内变化。
按照上述方法对接收信号进行极化滤波,再对0.05 s附近信号进行数据恢复。原始信号与滤波后信号时域图见图2,对滤波前后信号进行时频分析,分析结果见图3。
通过观察图2可以知道:瞬态干扰基本被抑制;由于过渡带的存在,滤波后输出信号与原信号稍微有些不同,考虑到过渡带时间远小于信号脉冲时间,可以基本忽略其对信号的负面影响;其他时间段内信号均被保留,信号所携带的信息基本没有损失。图3中,滤波后瞬态干扰完全被抑制,信号的线谱成分更加明显。
4.2 实测数据结果分析
实测数据的中心频率为600 Hz的单频矩形脉冲信号,截取存在瞬态干扰的一段信号进行分析,截取信号长度为0.05s,采样频率为10 kHz。
对信号加滑动窗,分析不同时刻偏振状态,提取极化参数,利用偏振状态变化情况对瞬态干扰进行抑制。联合利用3个极化参数,选取合适的标准差,设计极化滤波器,加权函数见图4。
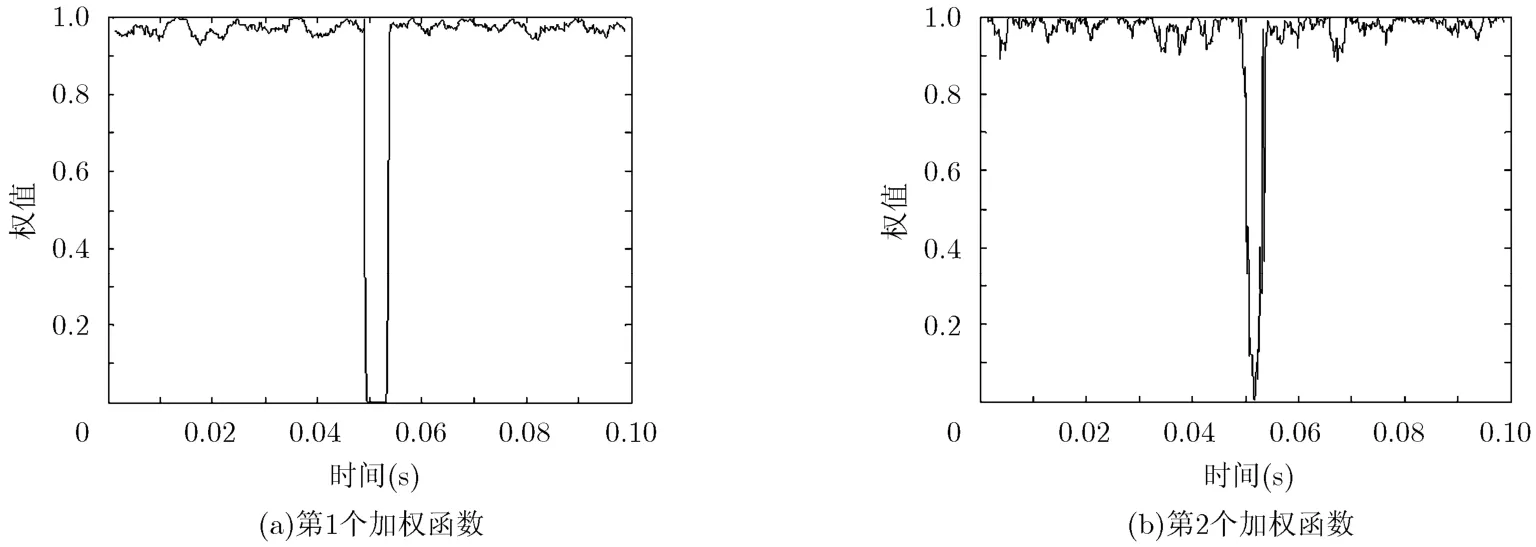
图1 根据偏振参数设计的极化滤波器加权函数
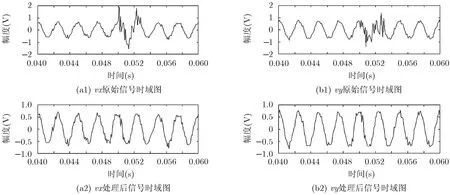
图2 原始信号与滤波后信号时域对比图
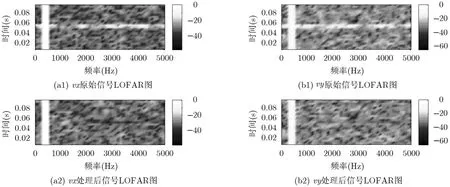
图3 原始信号与处理后信号LOFAR图

图4 实测信号对应的极化滤波器加权函数

图5 实测信号与滤波后信号对比图
第1个加权函数,在0.012-0.014 s时间段内,权值在0.7-0.9范围内变化;在0.031-0.033 s时间段内,权值的变化范围为0.2-0.5;其余时刻的权值在0.9-1.0范围内变化。第2个加权函数,在0.012-0.014 s时间段内,权值的变化范围是0.7-0.9;在0.031-0.033 s时间段内,权值的变化范围是 0.5-0.9;其余时刻权值在0.9-1.0范围内变化,两个权函数变化规律基本相同。
利用图4所示权函数对实测信号进行加权,实现滤波功能,对0.012-0.014 s和0.031-0.033 s时间段内信号进行数据恢复。原始信号与滤波后信号时域图见图5。
在图5中,瞬态干扰被很好地抑制,由于过渡带的存在,滤波后瞬态干扰旁边的信号与原始信号稍微有些不同。由于过渡带时间非常短暂,且滤波引起的变化很小,可以认为该方法能够抑制瞬态干扰,保留未受干扰污染的信号,并保证信号携带的信息基本没有损失。图6中,0.032 s附近的脉冲强度较大,0.13 s附近的瞬态干扰强度较弱,对比滤波前后信号的时频分析结果,可以看出通过滤波及数据恢复已将两处瞬态干扰去除。
5 结束语
当接收的矢量信号中混有瞬态干扰时,信号处理结果会受其影响,处理性能下降,必须对瞬态干扰进行抑制。本文提出了一种以偏振分析为基础的瞬态干扰消除方法。此方法通过极化滤波可直接去除瞬态干扰,利用调制函数能够比较直观的判断瞬态干扰的存在位置,不需要复杂计算,便于实现。仿真结果和实验数据均证明了该方法的有效性。

图6 实测信号与处理后信号LOFAR图
[1]杨德森, 洪连进. 矢量水听器原理及应用引论[M]. 第1版, 北京: 科学出版社, 2009: 41-45.
Yang De-sen and Hong Lian-jin. Vector Sensor Principle and Application[M]. 1st Edition, Beijing: Science Press, 2009:41-45.
[3]周忠根, 水鹏朗. 基于复数据经验模式分解的天波超视距雷达瞬态干扰抑制[J]. 电子与信息学报, 2011, 33(12):2831-2836.
Zhou Zhong-gen and Shui Peng-lang.Transient interference suppression based on complex empirical mode decomposition in over-the-horizon radar[J].Journal of Electronics&Information Technology, 2011, 33(12): 2831-2836.
[4]王阶, 刘涛, 陈晓旭, 等. 天波超视距雷达流星余迹瞬态干扰抑制方法[J]. 电子测量与仪器学报, 2009, 23(10): 67-72.
Wang Jie, Liu Tao, Chen Xiao-xu,et al..Method of meteor trail impulsive interference suppression in OTHR[J].Journal of Electronic Measurement and Instrument, 2009, 23(10):67-72.
[5]甄红飞, 龚耀寰, 刘涛. 基于TLS-ESPRIT 算法的OTHR瞬态干扰抑制[J]. 雷达科学与技术, 2011, 9(4): 341-346.
Zhen Hong-fei, Gong Yao-huan, and Liu Tao.Research on impulsive interference suppression in OTHR based on TLS-ESPRIT algorithm[J].Radar Science and Technology,2011, 9(4): 341-346.
[6]陈希信, 黄银河. 基于矩阵奇异值分解的高频雷达瞬态干扰抑制[J]. 电子与信息学报, 2005, 27(12): 1879-1882.
Chen Xi-xin and Huang Yin-he.A SVD-based approach of suppressing transient interference in high-frequency radar[J].Journal of Electronics&Information Technology, 2005,27(12): 1879-1882.
[7]Liu Tao, Chen Xiao-xu, and Wang Jie. Subspace impulsive interference suppression in OTHR[J].Progressin Electromagnetics Research, 2009, C(7): 167-181.
[8]Turley M. Impulsive noise rejection in HF radar using a linear prediction technique[C]. Radar Conference, United States, May 5-8, 2003, 9: 358-362.
[9]戴幻尧, 李永祯, 王雪松, 等. 基于和差波束极化特性的目标极化散射矩阵测量方法研究[J]. 电子与信息学报, 2010, 32(4):913-918.
Dai Huan-yao, Li Yong-zhen, Wang Xue-song,et al..A new target scattering matrix measurement algorithm based on polarization characteristics of sum-and-difference beam[J].Journal of Electronics&Information Technology, 2010, 32(4):913-918.
[10]刘勇, 李永祯, 戴幻尧, 等. 基于极化二元阵雷达的空域虚拟极化滤波算法[J]. 电子与信息学报, 2010, 32(11): 2746-2750.
Liu Yong, Li Yong-zhen, Dai Huan-yao,et al..The spatial virtual polarization filtering algorithm based on dual polarized antenna radar[J].Journal of Electronics&Information Technology, 2010, 32(11): 2746-2750.
[11]王克让, 朱晓华, 何劲. 基于矢量传感器MIMO雷达的DOD DOA和极化联合估计算法[J]. 电子与信息学报, 2012, 34(1):160-165.
Wang Ke-rang, Zhu Xiao-hua, and He Jin.Joint DOD DOA and polarization estimation for MIMO radar with electromagnetic vector sensors[J].Journal of Electronics&Information Technology, 2012, 34(1): 160-165.
[12]Alkaz V G, Ornofrash N I, and Perelberg A I. Polarization Analysis of Seismic Waves[M]. 1st Edition, Russian, Shtiintca Press, 1977: 100-105.
[13]Flinn E A. Signal analysis using rectilinearity and direction of particle motion[J].Proceedings of IEEE, 1965, 53(12):1874-1876.
[14]胡广书. 数字信号处理理论、算法与实现[M]. 第 2版, 北京:清华大学出版社, 2006: 527-574.
Hu Guang-shu. Digital Signal Processing Theory, Algorithm and Realization[M]. 2nd Edition, Beijing: Tsinghua University Press, 2006: 527-574.
