PDE模型在声纳图像去噪中的应用研究*

刘光宇，卞红雨，沈郑燕，石 红

（1.哈尔滨工程大学水声工程学院，黑龙江 哈尔滨 150001;2.总装备部，北京 100000）

0 引言

声纳图像处理包含了光学图像处理领域中的去噪、融合、分割、分类、识别、检索等各个方面。声纳图像与光学图像在成像原理与机制上有着本质的区别，虽然数字图像处理、模式识别与人工智能等学科已经发展比较成熟，但是很多可以用于光学图像处理的技术并不见得对声纳图像可行，并且有一些前沿的图像处理技术并没有在声纳图像处理中得到应用，因此，对声纳图像处理的研究工作是迫切需要的。图像去噪又是图像识别定位等后期处理的基础和前提，偏微分方程（partial differential equation，PDE）方法［1～7］在光学图像去噪中已有很多成功的应用，本文尝试将PDE模型用于声纳图像去噪处理，验证其有效性。

1 ROF模型

ROF 模型［8］是由 Fatemi，Osher和 Rudin 于 1992 年提出的一类典型的去噪方法，该模型是经典的变分偏微分方程针对“加性噪声”的去噪模型。

经典的TV模型［9］认为有噪声图像的全变分比无噪声图像的全变分大很多，因此，最小化全变分可以消除噪声。而在图像恢复中，为了在去噪的同时能够更有效地保留边缘，Rudin，Osher和Fatemi提出通过引入拉格朗日乘子，用BV空间的半范数——全变差来作为正则项来正则化TV模型，即ROF模型。

由此可得，ROF去噪模型可归结为如下能量泛函最小值问题

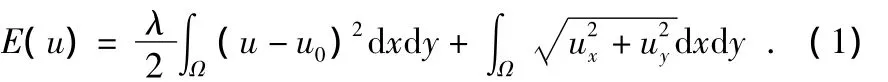
其中，第一项为保真项，它是根据噪声方差而定的逼近项，它使迭代后恢复的图像u尽可能保存原图像u0的特征;第二项为正则化项（regularized），它使得该模型在去噪的同时尽可能地保留图像的边缘特征信息;λ＞0为规整参数，在保真项和正则项之间起着平衡作用，对图像平滑意义重大。该模型的解是存在且唯一的，其能量泛函导出的Euler-Lagrange方程为

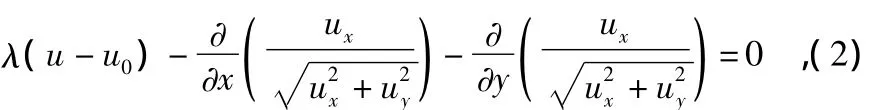
即

结合边界条件和初始条件由Euler-Lagrange方程得到的变分问题对应的梯度下降流方程为

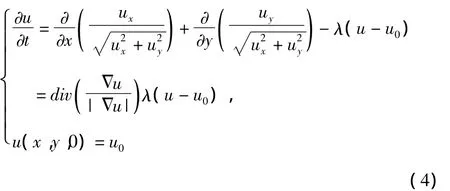
该模型在去噪的同时，能够很好地保持图像边缘，它的出现极大地推动了基于变分方法图像去噪的研究，但在去噪的同时会造成对比度丢失和阶梯效应等问题。

2 四阶扩散模型

ROF模型所对应的是二阶偏微分方程，而二阶偏微分方程处理图像时容易产生阶梯效应，而You-Kaveh模型应用四阶偏微分方程［10］，避免了二阶偏微分方程的阶梯效应问题。模型中，图像的正则能量为

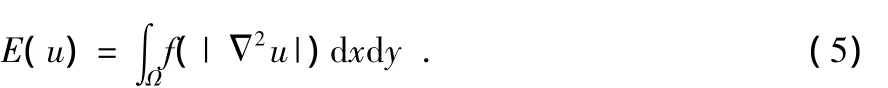
其对应的Euler-Lagrange方程为

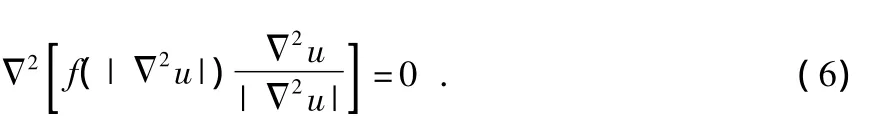
梯度下降流为

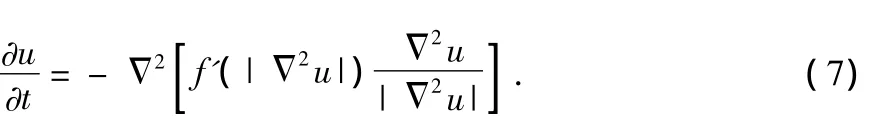
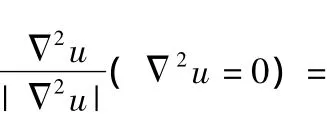
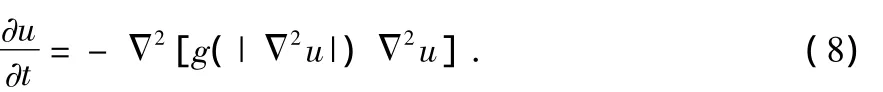
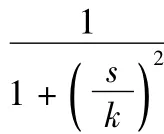
1）计算u二阶差分

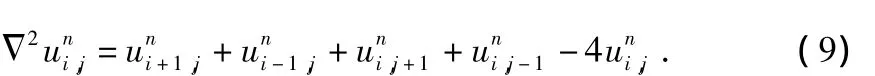
2）求函数g（s）

3）计算g（s）的二阶差分

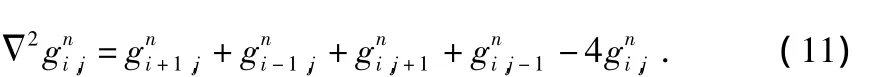
4）离散格式

3 实验结果与分析

选取如图1所示的大小为256×256的一幅侧扫声纳图像，分别加入均值为零，标准差为σn=0.1～0.6的高斯白噪声，利用ROF模型和四阶算子（FOD）模型进行去噪实验，噪声标准差为0.3时的去噪结果如图2所示。

图1 原始声纳图像Fig 1 Original sonar images

从图中可以明显看出:当噪声标准差比较大时，ROF模型去噪后的图像具有阶梯效应，图像细节非常模糊。四阶算子则避免了阶梯效应，图像细节更为清晰，但当受噪声污染严重时，四阶扩散模型的抗噪声能力明显下降，噪声去除的效果不很理想。

同样从客观角度对ROF和四阶算子的去噪性能进行比较，分别统计以上图像去噪前后的信噪比（SNR），峰值信噪比（PSNR），均方误差（MSE），得到的结果如表1所示，表中，NI为噪声图像，ROF_DI为ROF模型去噪图像，YK_DI为四阶扩散模型去噪图像。

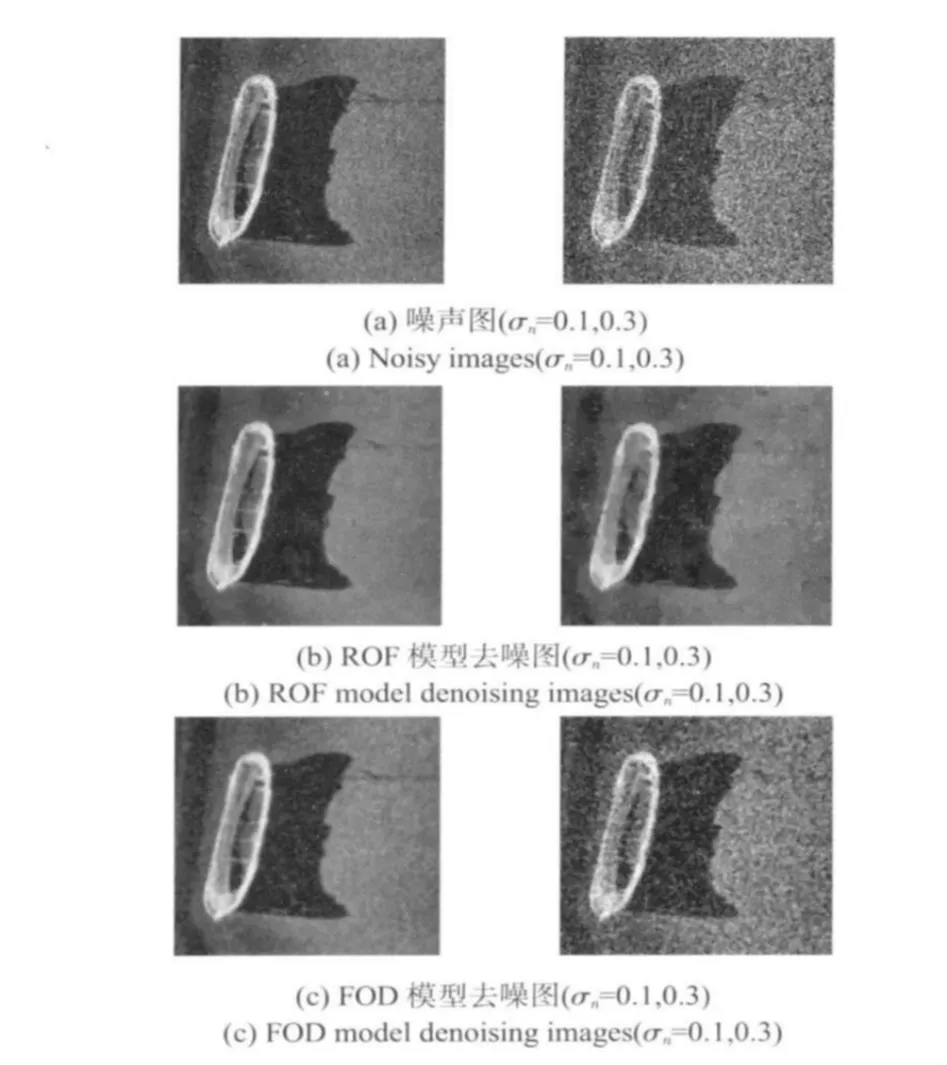
图2 去噪效果比较Fig 2 Comparison of denoising effect

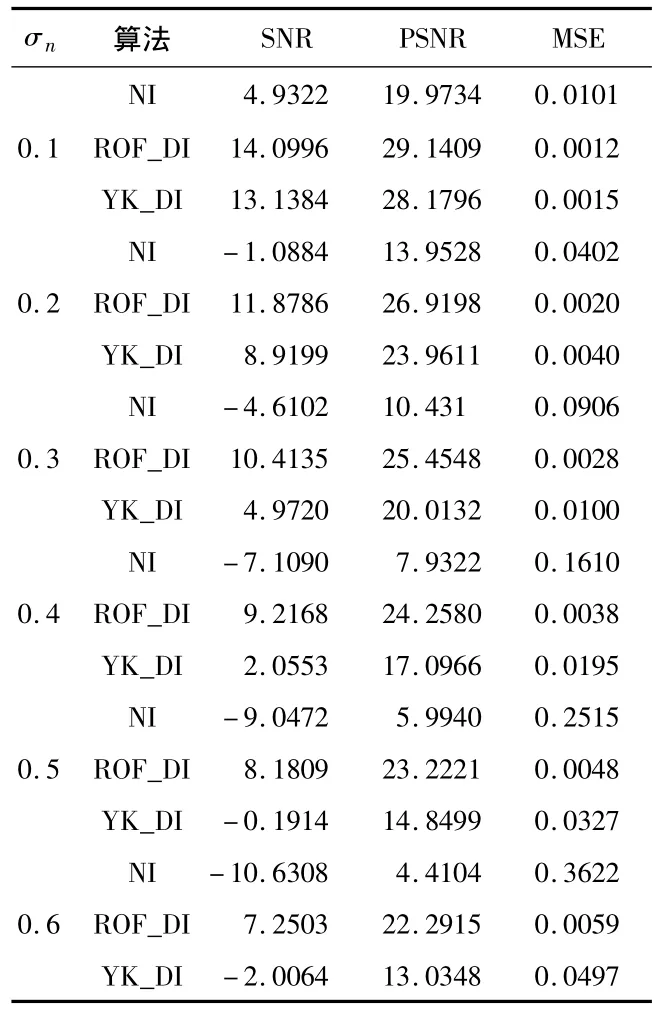
表1 SNR，PSNR及MSE比较Tab 1 Comparison of SNR，PSNR and MSE

从表中数据可以看出:ROF模型去噪后图像较四阶算子去噪后图像具有较高信噪比、峰值信噪比和较小的均方误差。所以，虽然四阶扩散模型有效避免了ROF模型的阶梯效应，一定程度上保持了边缘细节，但是该模型的抗噪声能力没有二阶的ROF模型好。

4 结束语

本文介绍了两种偏微分方程去噪模型—ROF模型和四阶扩散模型，并将这两种模型用于声纳图像去噪处理。ROF模型与四阶扩散模型的不同之处在于:ROF模型以二阶偏微分方程为基础，因此，不可避免地在去噪后产生明显的阶梯效应，图像出现模糊;实验中四阶扩散模型一定程度上改善了这种阶梯效应，但随着噪声标准差的增大，去噪效果急剧降低，当噪声标准差为0.6时，四阶扩散去噪后的SNR比ROF模型去噪低了近10 dB，已经不能满足声纳图像的去噪需要。综合来看，实际中的声纳图像去噪需要根据具体情况选择合适的模型进行处理。

［1］李兰兰.基于偏微分方程的图像复原和增强算法研究［D］.南京:东南大学，2004:1 －2.

［2］Barash D.A fundamental relationship between bilateral filtering，adaptive smoothing，and the nonlinear diffusion eqaution［J］.IEEE Transactions on PAMI，2002，24（6）:844 －847.

［3］Barash D，Comaniciu D.A common framework for nonlinear diffusing，adaptive smoothing，bilateral filtering and mean shift［J］.Image and Vision Computing，2004，22:73 －81.

［4］Black M J，Sapiro G，Marimont D H，et al.Robust anistropic diffusion［J］.IEEE Transactions on Image Processing，1998，7（3）:421－432.

［5］Perona P，Malik J.Scale-space and edge detection using anisotropic diffusion［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12（7）:629 －639.

［6］杨 新.图像偏微分方程的原理与应用［M］.上海:上海交通大学出版社，2003.

［7］Witkin.A scale-space filtering［C］//International Joint Conference on Artificial Intelligence，1983:1091 －1092.

［8］杜宏伟.基于偏微分方程的图像去噪综合模型［J］.计算机工程与应用，2008，44（20）:198 －201.

［9］李忠伟，潘振宽，倪明玖.基于TV模型的多相图像分割变分水平集方法［C］//第五届图像图形技术与应用学术会议，北京，2010:43－50.

［10］曾 超，王美清.一个基于四方向的拉普拉斯算子的四阶偏微分去噪方法［J］.福州大学学报:自然科学版，2008（1）:52－54.