子空间重构的一类自适应波束形成算法

杨志伟 贺 顺 廖桂生 刘 楠

①(西安电子科技大学雷达信号处理重点实验室 西安 710071)

②(西安科技大学通信学院 西安 710054)

1 引言

自适应波束形成[1-10](或自适应空域滤波)是阵列信号处理在雷达、声呐、通信等领域应用的热点问题，目的是在增强特定方向信号功率(称为目标信号或感兴趣信号)的同时抑制其它方向的来波信号(称为干扰)。与普通波束形成(或空域匹配滤波)不同，自适应波束形成是将维纳滤波理论应用到空域滤波中，它的加权矢量依赖于信号环境，在干扰或色噪声背景下能获得更大的输出信干噪比。但是，自适应波束形成算法在本质上属于统计信号处理范畴，如何在有限观察数据基础上高效快速地计算自适应加权矢量成为工程应用的关键。针对这一问题，国内外研究者提出了多种自适应权矢量的计算方法，包括采用迭代最小二乘算法(RLS)[11]提高最小均方误差算法(LMS)的收敛速度；采用降秩处理[12]方法改善小样本条件下采样协方差矩阵求逆算法(SMI)的处理损失；采用子空间跟踪方法[13,14]降低子空间投影类自适应波束形成算法的运算量。遗憾的是，上述方法均未考虑多维域阵列数据的结构特性。此外，在文献[15,16]中提出将高维权矢量分解为多个低维权矢量的自适应波束形成方法，降低了估计相关矩阵的采样数据和运算量。但是，该方法需要采用双迭代算法进行低维权矢量寻优，迭代次数难以确定。

事实上，多维阵列的全维数据能由分维数据表示。例如空时两维阵列数据能够表示成空域数据与时域数据的张量积形式，空-极化两维阵列数据能够表示成空域数据与极化数据的张量积形式，空-时-极化3维阵列数据矢量能够表示成空域数据、时域数据和极化数据的张量积形式。虽然对多维阵列的全维数据采用分维级联处理的方式能够在一定程度上降低全维处理的运算复杂度和放松对独立同分布样本数的要求，但是损失了输出信干噪比。

针对上述问题，本文在子空间投影类波束形成算法基础上，提出由分维信号子空间重构全维真实信号子空间的自适应波束形成算法。该方法首先在训练样本集上计算分维阵列数据的主特征矢量并构成相应的分维信号子空间；然后通过张量积操作和自适应交叉项剔除重构真实的全维信号子空间；最后根据子空间投影算法计算波束形成权矢量。仿真结果表明本文方法具有较低的运算复杂度和要求更小的独立同分布训练样本集规模，能获得与最优处理相近的输出信干噪比。

2 信号模型

不失一般性，在窄带远场平面波假设下，k时刻的多维阵列数据X(k)可表示为

其中H0假设表示接收数据仅由干扰和噪声组成，H1假设表示接收数据包含目标信号；a0和s0(k)分别表示目标信号的阵列导向矢量(或称为阵列流形)和复包络；AJ=[a1…aP]和sJ(k) = [s1(k)…sP(k) ]T分别表示P个干扰信号的阵列流形和复包络；N(k)表示零均值的加性高斯白噪声。

一般地，多维阵列数据的阵列导向矢量可表示成a=b⊗c的形式(符号⊗表示向量的张量积，矢量a,b,c的长度分别为L,M,N)。例如，就空时均匀采样阵列而言，假设沿阵面线性排列M个空域接收通道和相干积累N个时域脉冲，采用自发自收工作模式，理想情况下的阵列导向矢量可表示为

其中fs和fd分别表示空间角频率和归一化多普勒频率。

在目标信号、干扰、噪声不相关假设下，阵列数据的协方差矩阵可表示为

众所周知，基于线性约束最小方差准则(LCMV)的加权矢量可根据式(4)计算。

显然，考虑干扰的信号子空间对应特征值通常远大于噪声子空间对应特征值，自适应加权矢量主要位于噪声子空间内。因此，在忽略非零常数后，根据式(6)计算的基于子空间投影的波束形成权矢量wSP与wLCMV近似相等。

3 改进算法

有效降低运算量和提高加权矢量在小样本条件下的收敛速度是自适应波束形成算法获得工程应用的关键，本文结合多维阵列数据的结构特性，提出利用分维信号子空间重构真实的全维信号子空间的方法来提高权矢量的收敛速度和降低运算量。下面给出本文所提方法的详细描述。

3.1子空间重构

在H0假设下，根据多维阵列数据可分维重构的特点，分维的阵列数据可表示为

相应地，基于最大似然准则的分维阵列数据协方差矩阵采用式(8)进行估计。

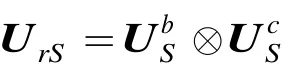
显然，Tb⊗Tc为满秩矩阵，UrS和BJ⊗CJ张成的列空间相同，即

3.2 交叉项剔除

一方面考虑同时多个信号源条件下UrS的列向量与阵列导向矢量缺乏一一对应关系，直接判断交叉项存在困难；另一方面鉴于交叉项AR仅由矩阵张量积操作引入，实际的多维阵列数据中并不存在任何与交叉项相对应的来波信号。因此，本文在重构干扰流形基础上通过最小冗余的最优阵列数据拟合来自适应剔除交叉项。

不失一般性，记重构的干扰流形为ArS=[a1…aQ]。相应地，在H0假设下，多维阵列数据X(k)在ArS上的最优拟合系数可根据式(12)计算

进而可求解得到

事实上，我们无法预知干扰源数目，只能通过对数据矢量y进行分析来估计干扰源数目。尽管有信息论准则(AIC)或最短描述长度准则(MDL)[17]等方法可供采用，但在低信噪比或快拍数较少情况下y中的小值元素可能存在扩散问题，影响干扰源数目的正确判断。为此，本文采用顺序法对干扰子空间进行最小冗余估计。具体步骤如下：

步骤 1 初始化干扰的阵列流形ArJ为空矩阵，交叉项的阵列流形ArR=ArS和数据矢量Z(k) =X(k)；

步骤 6 估计出重构的真实干扰流形ArJ。

一旦计算出真实的干扰流形ArJ，相应的加权矢量按式(14)计算：

3.3 运算复杂度分析

众所周知，对全维处理情况，采样协方差矩阵求逆算法的运算复杂度为O((M×N)3)。本文方法采用分维重构的方式估计真实的全维干扰流形，在估计分维数据的干扰流形过程中需要首先获得干扰的波达参数，以求根 MUSIC算法为例，考虑特征分解和求根操作后的总运算复杂度近似为O(M3+(2(M- 1))3+N3+(2(M- 1))3) ≈O(9(M3+N3))；采用矩阵张量积重构全维干扰流形的运算复杂度为O(M×N×Q)(其中Q表示重构干扰流形的列数)；剔除交叉项的运算复杂度近似为O((Q-P)(Q3+M×N×Q2+ (M×N)2×Q))(其中P表示重构真实干扰流形的列数)。在全维处理器维数M×N较大条件下，本文方法与采样协方差矩阵求逆算法的运算复杂度之比约为[(Q-P)×Q]/(M×N)。考虑干扰源数目通常较少，因此本文方法具有较低的运算复杂度。

4 仿真实验

本节通过计算机仿真实验检验所提方法的有效性。做为对比，记本文方法为 SRC-BF，记基于特征分解的波束形成方法为EVD-BF，记基于采样协方差矩阵求逆的波束形成方法为SMI-BF。

实验1空时均匀采样阵列工作在远场窄带模式，具有6个空域接收通道和相干处理16个时域脉冲，同时接收3个等功率的干扰信号(干噪比JNR=20 dB)。实验中满足独立同分布条件的训练样本数为256, 3个干扰的归一化空间角频率和归一化多普勒频率满足彼此间的最小间隔0.15且在±0.8内均匀分布。图1～图3给出了无误差条件下经1000次蒙特卡罗实验获得的阵列数据空时谱。可以发现：与重构的全维信号子空间UrS对应的空时谱在干扰位置之外还存在多个谱峰(与交叉项对应)，导致直接根据UrS计算的加权矢量可用自由度减少，潜在地会导致输出信干噪比下降；与重构的真实干扰流形ArJ对应的空时谱仅在干扰位置存在谱峰，说明本文方法能有效剔除交叉项，且有望获得与US相近的输出信干噪比。

实验2空时均匀采样阵列工作在远场窄带模式，具有6个空域接收通道和相干处理8个时域脉冲，同时接收3个非等功率的干扰信号和1个目标信号，干噪比依次是10 dB, 20 dB和30 dB，信噪比5 dB。实验中3个干扰的归一化空间角频率和归一化多普勒频率满足彼此间的最小间隔0.15且在±0.8内均匀分布，目标与干扰的归一化空间角频率和归一化多普勒频率满足彼此间的最小间隔为 0.1且在±0.5内均匀分布。图 4给出了无误差条件下经1000次蒙特卡罗实验获得的输出信干噪比随同分布训练样本数的变化关系。可以发现：在小样本条件下，例如训练样本数小于 2倍信号子空间维数，SRC-BF算法能获得更大的输出信干噪比，表明本文方法相比全维数据特征分解而言能获得更为精确的子空间估计结果，这非常有利于工程应用；随着样本数的增加，SRC-BF算法相比SMI-BF算法而言能获得与 EVD-BF算法更为接近的输出信干噪比，表明本文方法能有效提高自适应波束形成算法的干扰抑制能力和收敛速度。

图1 根据US计算的空时谱

图2 根据UrS计算的空时谱

图3 根据ArJ计算的空时谱

图4 输出信干噪比随训练样本数的变化关系

5 结论

全维自适应波束形成算法运算量巨大和要求满足独立同分布条件的训练样本集规模庞大是制约工程应用的主要因素。针对这一问题，本文基于多维阵列数据可分维重构这一特点，从子空间投影类波束形成算法出发，提出结合子空间重构和交叉项剔除的权矢量计算方法。该方法具有较低的运算复杂度和能有效提高子空间估计精度，可提高自适应波束形成算法在小样本条件下的输出信干噪比。

[1]Allen B and Ghavami M. Adaptive Array Systems,Fundamentals and Applications[M]. Chichester, UK, Wiley,2005, Chapter 1.

[2]Li J and Stoica P. Robust Adaptive Beamforming[M].Hoboken, NJ, Wiley, 2005: 1-47.

[3]齐维孔, 禹卫东, 祁海明. 星载MIMO-SAR与距离向DBF相结合系统研究[J]. 电子学报, 2010, 38(10): 2251-2257.

Qi Wei-kong, Yu Wei-dong, and Qi Hai-ming. Study of the system combining spaceborne MIMO-SAR and elevation DBF[J].Acta Electronica Sinica, 2010, 38(10): 2251-2257.

[4]刘聪锋, 廖桂生. 最差性能最优通用信号模型稳健波束形成算法[J]. 电子学报, 2010, 38(6): 1249-1255.

Liu Cong-feng and Liao Gui-sheng. Robust beamforming algorithm for general signal models using worst-case performance optimization[J].Acta Electronica Sinica, 2010,38(6): 1249-1255.

[5]戴凌燕, 王永良, 李荣锋, 等. 基于不确定集的稳健Capon波束形成算法性能分析[J]. 电子与信息学报, 2009, 31(12):2931-2936.

Dai Ling-yan, Wang Yong-liang, Li Rong-feng,et al..Performance analysis of robust Capon beamforming based on uncertainty set[J].Journal of Electronics&Information Technology, 2009, 31(12): 2931-2936.

[6]任超, 吴嗣亮, 王菊, 等. 基于空时处理的稳健自适应波束形成算法[J]. 电子与信息学报, 2009, 31(6): 1381-1385.

Ren Chao, Wu Si-liang, Wang Ju,et al.. A robust adaptive beamforming algorithm based on space-time processing[J].Journal of Electronics&Information Technology, 2009, 31(6):1381-1385.

[7]冯杰, 杨益新, 孙超. 低频共形阵的宽带波束域高分辨方位估计方法[J]. 系统工程与电子技术, 2008, 30(1): 24-27.

Feng Jie, Yang Yi-xin, and Sun Chao, Broadband beamspace DOA estimation algorithms for low frequency conformal array[J].Systems Engineering and Electronics, 2008, 30(1):24-27.

[8]晋良念, 欧阳缮, 谢跃雷, 等. 基于稳健波束形成的超宽带穿墙成像方法[J]. 系统工程与电子技术, 2011, 33(1): 208-212.

Jin Liang-nian, Ou-yang Shan, Xie Yue-lei,et al.. Ultrawideband through-the-wall imaging based on robust adaptive beamforming[J].Systems Engineering and Electronics, 2011,33(1): 208-212.

[9]李关防, 惠俊英. 基于经验模态分解的模态域 MVDR方法研究[J]. 电子学报, 2009, 37(5): 942-946.

Li Guan-fang and Hui Jun-ying. A study of mode domain MVDR algorithm based on empirical model decomposition[J].Acta Electronica Sinica, 2009, 37(5): 942-946.

[10]钱琛, 杨益新, 郭国强. 球体表面圆环阵模态域稳健高增益波束形成方法研究[J]. 声学学报, 2010, 35(6): 623-633.

Qian Chen, Yang Yi-xin, and Guo Guo-qiang. On robust supergain beamforming in mode space for a circular array mounted on a sphere[J].Acta Acustica, 2010, 35(6): 623-633.

[11]Vega L R, Benesty H R J, and Tressens S. A fast robust recursive least-squares algorithm[J].IEEE Transactions on Signal Processing, 2009, 57(3): 1209-1216.

[12]Strobach P. Low-rank adaptive filters[J].IEEE Transactions on Signal Processing, 1996, 44(12): 2932-2947.

[13]Badeau R, David B, and Richard G. Fast approximated power iteration subspace tracking[J].IEEE Transactions on Signal Processing, 2005, 53(8): 2931-2941.

[14]Doukopoulos X and Moustakides G. Fast and stable subspace tracking[J].IEEE Transactions on Signal Processing, 2008,56(4): 1452-1465.

[15]吕晖, 冯大政, 和洁, 等. 机载MIMO雷达两级降维杂波抑制方法[J]. 电子与信息学报, 2011, 33(4): 805-809.

Lu Hui, Feng Da-zheng, He Jie,et al.. Two-stage reduced-dimension clutter suppression method for airborne MIMO radar[J].Journal of Electronics&Information Technology, 2011, 33(4): 805-809.

[16]和洁, 冯大政, 吕晖, 等. 基于相关域的二维自适应波束形成算法[J]. 电子与信息学报, 2010, 32(12): 2890-2894.

He Jie, Feng Da-zheng, Lu Hui,et al.. Two-dimensional adaptive beamforming based on correlation matrix[J].Journal of Electronics&Information Technology, 2010,32(12): 2890-2894.

[17]Wax M and Kailath T. Detection of signals by information theoretic criteria[J].IEEE Transactions on Acoustics, Speech,and Signal Processing, 1985, 33(2): 387-392.