基于鲁棒Capon波束形成的探地雷达成像算法

周 琳 黄春琳 粟 毅

(国防科技大学电子科学与工程学院 长沙 410073)

1 引言

探地雷达(Ground Penetrating Radar, GPR)成像技术可以对地下目标进行非破坏性的高分辨率检测和识别，已在军事和民用领域得到广泛应用[1,2]。目前常用的 GPR成像方法主要有反向投影(Back Projection, BP)算法[3,4]、距离迁移(Range Migration,RM) 算法[5,6]、衍射层析(Diffraction Tomography,DT)算法[7,8]等，现有算法均属于独立于数据的非自适应信号处理方法。尽管使用这些算法可以实现比较高的分辨率，但与依赖于数据的自适应信号处理方法相比，后者具有更高的旁瓣和杂波抑制能力。

Capon波束形成方法(Capon Beamforming, CB)作为典型的自适应信号处理方法，已广泛应用于阵列信号处理、SAR成像等领域[9]。但是在某些实际应用中，信号方向矢量往往不能准确估计，此时 CB的性能将急剧下降，甚至比非自适应方法的性能还差。为此许多文献对改进CB的鲁棒性开展了研究，试图解决由方向矢量不确定性导致的估计不准问题，例如基于线性约束的协方差矩阵渐变方法[10]，基于二次约束的对角加载方法[11]，基于噪声协方差矩阵先验知识的子空间自适应波数形成方法[12]等，但这些方法并未直接针对方向矢量的不确定性。

鲁棒 Capon波束形成(Robust Capon Beamforming, RCB) 方法在CB的基础上考虑了基于球形或椭球形不确定集的方向矢量，克服了原有CB进行估计时鲁棒性差的缺点，在穿墙成像、医学成像等领域已得到成功应用[13-16]。本文将上述自适应方法应用于GPR成像处理中，提出了基于RCB理论的GPR成像算法，并得到了很好的旁瓣和杂波抑制效果。全文按照如下结构组织，第2节介绍了RCB基础理论，第3节提出了基于RCB的GPR成像方法，第4节给出了实测数据实验结果，最后是结束语。

2 RCB基础理论

对于一个包含M个阵元的线性阵列，假设其接收数据的协方差矩阵为R, RCB方法的关键是获得阵列加权矢量w，该加权矢量可通过在如下线性约束条件下寻找最小值得到[13]：

其中as为阵列输出方向矢量，上标H在本文中均表示共轭转置。由于实际情况中as不能精确已知，关于as仅有的先验知识是其在附近一个很小的邻域内波动，即，其中e为一个很小的正数。令s2为后向散射信号能量，则上式可转化为

由于式(2)中s2与as均为未知，故二者之间存在尺度模糊，为消除这种影响，应使用如下范数约束[14]：

对于任意时刻t，式(2)的解为

这样式(2)可退化为如下二次最优问题：

式(5)中为避免as=0，需设定限制条件[14]：

为求解式(5)，使用 Lagrange乘数法，令目标函数为

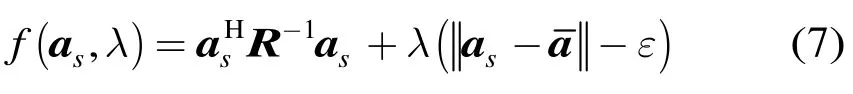
其中l≥0为实Lagrange乘数，且满足R-1+lI正定。这样对于固定的l,f(as,l)最小化的条件是[14]

并且有

联立式(8)与式(9)可得到关于 Lagrange乘数l的方程：

为求解式(10)，首先可将协方差矩阵R进行特征值分解：

其中U为R的特征矢量矩阵，其每一列都为R的特征矢量，Γ为对角化特征值矩阵，其主对角线上的各元素对应于R的M个特征值：g1≥g2≥…≥gM。令z=[z1,z2,… ,zM]T=UH，则式(10)可转化为

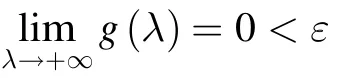
则后向散射信号能量可通过将式(13)代入式(4)求得，而阵列加权矢量w可表示为

3 基于RCB的GPR成像算法

由于 RCB在理论上具有良好的旁瓣和杂波抑制能力，为此本文将其应用到GPR成像中，提出了基于RCB的GPR成像算法。首先建立2维成像场景如图1所示，整个场景被直线z=0分为两部分。z＜ 0 的区域为空气，其介电常数为e1=e0，其中e0是自由空间中的介电常数。z＞0区域为各向同性均匀的土壤，其介电常数为e2=er e0，其中er是土壤的相对介电常数。为简化模型，假设两个区域内的磁导率都等于自由空间中的磁导率，即m1=m2=m0，其中m1,m2,m0分别为空气中、土壤中和自由空间中的磁导率，并假定空气和土壤均无耗。考虑GPR中典型的B-scan合成孔径扫描方式，假设合成孔径数目为M，当前工作的天线位置序号为k，用黑色的三角形表示，坐标为(xk, -h)，其余M-1个孔径位置由灰色三角形表示。

第k个孔径处接收到的信号可表示为

其中t= 1Δt, 2 Δt, … ,NΔt, Δt为时域采样间隔。对图1中给定的某成像点A，首先要计算出从A到各天线位置处的双程时延。由于空气-土壤交界面的影响，该路径不是一条直线而是一条折线。发射信号从第k个天线位置出发，经过折射点(xr,0)到达点A，再沿原路径返回天线处。入射角和折射角分别用qi和qt表示。

图1 成像场景说明

对于任意一个成像点A，根据Snell定律，有如下关系：

由图1中坐标关系，式(16)可转化为

式(17)是一个关于xr的四次方程，通过求解xr，可得到双程时延表达式如下所示：

其中c是自由空间中电磁波的波速，tA,k即对应于点A和第k个天线之间的双程时延。利用式(18)所得时延，可将原始回波数据进行时延校正如下：

则在某时刻t的M个阵元的校正后接收信号可表示为

为了估计as及w，首先需要估计接收数据的协方差矩阵R。各种基于CB的自适应方法的一个主要差别就是关于协方差矩阵的不同假设及构造方法[15]。一种直观的构造方法即利用y(t)直接生成协方差矩阵R：

但是因为合成孔径扫描方式未能对场景提供足够多的视，按照式(21)构造的协方差矩阵会降低算法抑制旁瓣和杂波的能力，为此需将接收数据划分为多个子集以增加可用视数[9]。利用文献[9]提出的划分子集方法，本文在时域上将M×1维的校正后信号y(t)划分为L个相互重叠的N×1维的信号yi(t) ,i= 1,2,… ,L，图 2是该划分方法的示意图，由图2可知L=M-N+ 1。采用降低信号的维度从而生成多视的方法来构造协方差矩阵会一定程度上降低成像分辨率，为减小这种效应，N不应过小，文献[15]中关于N的经典取值为N=0.8M。使用较大的N会增加算法中矩阵不可逆的可能性，但另一方面会使成像分辨率没有大幅降低的同时保持算法的高信杂比和高峰值旁瓣比特性。本文中协方差矩阵定义为

图2 将校正信号划分为子集示意图

下面便可按照上节介绍的RCB理论进行GPR成像，当求得加权矢量的估计值后，则t时刻点A处的后向散射信号s(t)为

点A处的后向散射能量可通过式(24)计算[16]：

将后向散射能量p(A)作为点A处的成像值，通过遍历待成像区域的所有点，便完成成像过程。综上所述，本文提出的基于RCB的GPR成像算法的具体步骤如下：

步骤 1 对成像区域中任意一点，按照式(18)计算其距离M个合成孔径位置的双程时延，再按照式(19)得到校正后信号y(t)；

步骤 2 利用y(t)按照式(22)构造协方差矩阵R；

步骤 3 将R按照式(11)进行特征值分解，从而求得U,Γ及z；

步骤 4 利用Γ和z求解式(12)中的 Lagrange系数l0；

步骤 5 利用l0及式(8)，式(13)，式(14)求解,和；

步骤 7 按照上述步骤，遍历整个成像区域。

4 实验结果及分析

第1个实验使用GPRMax软件生成的仿真数据进行分析。实验场景如图 3(a)所示，两根钢筋棍埋设于相对介电常数为4的各向均匀土壤中，钢筋均沿y轴放置，场景剖面具体的几何位置关系见图3(b)。深度为10 cm的钢筋直径为0.5 cm，深度为25 cm的钢筋直径为1 cm。GPR天线距地面10 cm,B-scan路径沿x轴方向，每个合成孔径扫描位置在图中用黑色圆点表示。发射信号为高斯微分脉冲，中心频率为1 GHz。

图3 仿真数据成像实验的场景说明

图 4(a)是使用本文所提 RCB算法进行成像的归一化结果。考虑到 BP算法是传统的非自适应算法中的典型代表，且可以充分考虑介质的分层现象，其在 GPR成像理论和实际中都已得到深入研究和广泛应用，故本文选取BP算法的结果与RCB算法进行比较，如图4(b)所示。

由图4可以看出，使用RCB算法可得到视觉上非常直观的旁瓣和杂波抑制效果。为了定量描述杂波抑制的效果，本文使用积分旁瓣比(Integrated Side Lobe Ratio, ISLR)和峰值旁瓣比(Peak Side Lobe Ratio, PSLR)对成像质量进行评价。ISLR定义为目标所有旁瓣能量和主瓣能量的比值：

其中Etotal和Emain分别是图像中总的能量和目标主瓣能量。PSLR定义为目标第一副瓣峰值和主瓣峰值的幅度之比：

其中Iside和Ipeak分别是图像目标处旁瓣的最大幅值和主瓣的最大幅值。

表1给出了两种算法成像结果中各目标的ISLR和PSLR值，可见与BP算法相比，RCB算法各个指标均有所下降，这说明RCB算法的成像结果中能量更加集中在目标区域，即其更好地抑制了非目标区域的干扰。在图4中通过观察两种成像算法结果中目标峰值处的主瓣-3 dB宽度，对于左上方目标，在x方向上，RCB算法为BP算法的0.81倍，在z方向上，RCB算法为BP算法的0.80倍；对于右下方目标，在x方向上，RCB算法为BP算法的0.89倍，在z方向上，RCB算法为BP算法的0.67倍。主瓣宽度的缩小进一步说明 RCB算法在分辨率上也较BP算法有一定程度的提高。

表1仿真数据成像结果性能对比

第2个实验使用实测数据进行分析，一个装满纯净水的矿泉水瓶被埋于沙坑中，如图 5(a)所示。沙子的相对介电常数为 2.37。水瓶的长度方向沿y轴放置，中心深度为 17 cm，水瓶主体部分横截面直径为7 cm。天线距地面40 cm, B-scan路径沿x轴方向，横穿水瓶中心，每个合成孔径扫描位置在图5(a)中用黑色圆点表示，水瓶的B-scan横截面示意图如图5(b)所示。本实验中所使用的发射信号与实验1中相同。

图4 仿真数据成像结果对比

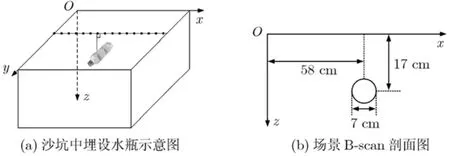
图5 实测数据成像实验的场景说明

图6是分别使用RCB算法和BP算法进行成像的结果，表2给出了两种算法成像结果的ISLR和PSLR，再次说明了RCB算法的干扰抑制性能。

为了更好地观察到 RCB算法在分辨率上的性能，图7给出了两种算法成像结果中峰值点位置在x和z两个方向的剖面图。考虑目标峰值处的主瓣-3 dB宽度，在x方向上，RCB算法为BP算法的0.75倍，在z方向上，RCB算法为BP算法的0.71倍，再次说明 RCB算法可以在一定程度上提高成像分辨率。

表2 实测数据成像结果性能对比

5 结束语

现有的 GPR成像算法均属于独立于数据的非自适应信号处理方法，考虑到依赖于数据的自适应信号处理方法在干扰抑制方面的优良性能，本文将RCB理论应用于GPR成像中，不仅大幅降低了成像结果中旁瓣和杂波的能量，并在一定程度上提高了成像分辨率。但是在成像质量提高的同时，由于RCB算法中涉及大量的矩阵求逆运算，其计算量也急剧增加，为此如何提高RCB算法的计算效率将成为下一步的研究重点。

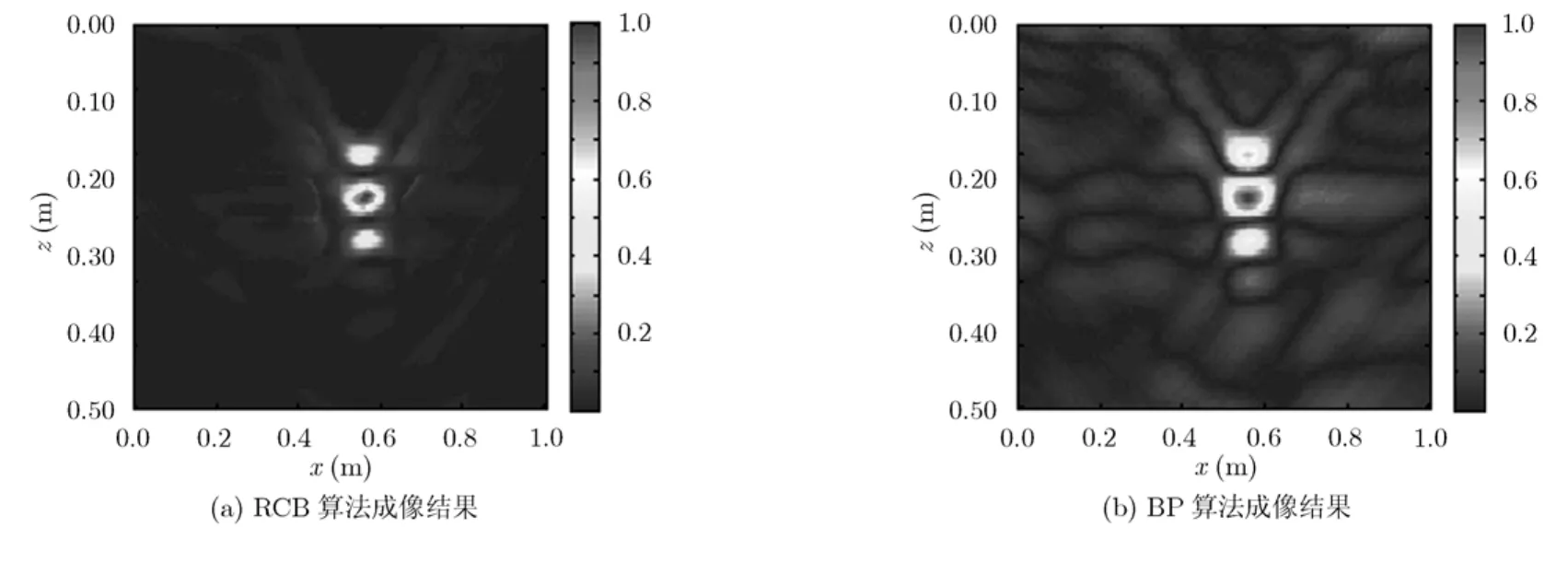
图6 实测数据成像结果对比

[1]粟毅, 黄春琳, 雷文太. 探地雷达理论与应用[M]. 北京: 科学出版社, 2006: 1-10.

Su Yi, Huang Chun-lin, and Lei Wen-tai. Theory and Applications of Ground Penetrating Radar [M]. Beijing:Science Press, 2006: 1-10.

[2]Khan U S, Al-Nuaimy W, and Abd El-Samie F E. Detection of landmines and underground utilities from acoustic and GPR images with a cepstral approach [J].Journal of Visual Communication and Image Representation, 2010, 21(7):731-740.

[3]Zhou L and Su Y. A GPR imaging algorithm with artifacts suppression[C]. Proceedings of the 13th Internarional Conference on Ground Penetrating Radar, Lecce, Italy, 2010:331-337.

[4]Chen Lei and Shan Ouyang. A time-domain beamformer for UWB through-wall imaging [C]. IEEE Region 10 Conference,Taipei, China, 2007: 1-4.

[5]Zyada Z, Matsuno T, Hasegawa Y,et al.. Advances in GPR-based landmine automatic detection [J].Journal of the Franklin Institute, 2011, 348(1): 66-78.

[6]Schmelzbach C, Tronicke J, and Dietrich P. Threedimensional hydrostratigraphic models from groundpenetrating radar and direct-push data [J].Journal of Hydrology, 2011, 398(3/4): 235-245.

[7]Dafflon B, Irving J, and Barrash W. Inversion of multiple intersecting high-resolution crosshole GPR profiles for hydrological characterization at the Boise Hydrogeophysical Research Site(BHRS)[J].Journal of Applied Geophysics, 2011,73(4): 305-314.

[8]Hugenschmidt J, Kalogeropoulos A, Soldovieri F,et al..Processing strategies for high-resolution GPR concrete inspections [J].NDT&E International, 2010, 43(4): 334-342.

[9]Benitz G R. High-definition vector imaging [J].Proceedings of the31st Lincoln Laboratory Journal, 1997, 10(2): 147-170.

[10]Zatman M. Comments on theory and applications of covariance matrix tapers for robust adaptive beamforming [J].IEEE Transactions on Signal Processing, 2000, 46(6):1796-1800.

[11]Wu R, Bao Z, and Ma Y. Control of peak sidelobe level in adaptive arrays [J].IEEE Transactions on Antennas and Propagation, 1996, 44(10): 1341-1347.

[12]Lee C C and Lee J H. Robust adaptive array beamforming under steering vector errors [J].IEEE Transactions on Antennas and Propagation, 1997, 45(1): 168-175.

[13]Li J, Stoica P, and Wang Z. On robust Capon beamforming and diagonal loading [J].IEEE Transactions on Signal Processing, 2003, 51(7): 1702-1715.

[14]Xie Y, Guo B, Xu L,et al.. Multi-static adaptive microwave imaging for early breast cancer detection [C]. Proceedings of 39th ASILOMAR Conference on Signals, Systems and Computers, Pacific Grove, Calif, USA, 2005: 285-289.

[15]Ahmad F, Amin M G, and Kassam S A. A beamforming approach to stepped-frequency synthetic aperture throughthe-wall radar imaging [C]. Proceedings of 1st IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP 2005), Puerto Vallarta, Mexico, 2005: 24-27.

[16]Xie Y, Guo B, Li J,et al.. Novel multistatic adaptive microwave imaging methods for early breast cancer detection[J].EURASIP Journal on Applied Signal Processing, 2006:1-13.