基于锁相放大技术的激光超声信号处理电路的设计

金宝印，Dante Dorantes，白茂森，孙凤鸣，李艳宁，陈 治，胡小唐

（天津大学精密测试技术及仪器国家重点实验室，天津 300072）

0 引言

亚微米尺度下的表面和亚表面效应对于科学研究与工业运用具有重要意义，已经得到了广泛的应用，比如:1）薄膜是微机电系统（MEMS）的重要组成部分［1，2］;2）在微电子工业中，必须时刻对集成电路的薄膜厚度和粗糙度在线监测［3～5］;3）航空领域的表面涂层、切割刀具的耐磨涂层以及固态装置的弥散层的应用［6］;4）薄膜具有良好的纳米摩擦学性能，广泛应用于非易失性随机存取存储器;5）用于纳米元件，如作为液体和固体的表层、纳米管、纳米线、纳米谐振腔和纳米原子链等;6）用于生物技术、生物材料以及涂料等［7］。

因此，如何对薄膜材料的机械特性（如杨氏模量、厚度、密度等）进行准确的测量显得十分重要。测量杨氏模量的现有技术主要包括纳米压痕测试技术、布里渊散射技术和激光声表面波技术（LSAW）［8～10］。其中纳米压痕测试技术是一种接触式测量，会对样品表面造成一定的损伤，布里渊散射技术是一种耗时的测量方法其获得的散射波的振幅远小于其他方法获得的振幅，而LSAW技术是一种无损的技术，又具备快速，精确测量等特点，以及具有原位且同步测量的能力，故而被视作测量薄层机械特性（厚度低于1 m），柔软或硬脆薄层（很高的孔隙率）的最有效方法之一［11］。SAW的能量集中于表面下1～2个波长范围，适合测量表面和亚表面的薄膜特性，其能量会随着传播深度的增加呈指数衰减，频率越高，衰减越快。

1 实验系统

鉴于LSAW技术优越的性能，本文设计了一套基于Sagnac干涉仪的LG/LD-SAW信号检测系统，系统结构如图1 所示［12，13］。

图1 系统结构图Fig 1 Structure diagram of system

本文所用的激光器为二极管泵浦被动可调Q激光器，波长532/1064 nm可调，532 nm下单脉冲能量0.5 mJ，脉冲持续时间800 ps，重复频率0～2 kHz可调，样品为镀有SiO2薄膜的Si样品。实验过程如下:脉冲激光器经过一分束镜分成两束光，一束作为激发光束，另一束作为检测光束，激发光束通过激光准直扩束单元到达样品表面，瞬间的热效应激发薄膜样品产生SAW，并沿样品表面传播;检测光束经过声光调制器调制后，通过Sagnac干涉仪检测某一时间点处的SAW信号，之后将检测信号传入光电探测器，转换为电信号输出，经过锁相放大单元的处理，将高频微弱信号转换为直流低频信号检测出来，并送入PC，对信号进行存储与处理，并通过PC控制电动位移平台，检测不同位置处的SAW信号。而且，通过调整激发单元中的光程调节单元，能够控制检测光束到达样品表面的时间，检测不同时间点处的信号，从而恢复SAW信号，并计算出薄膜的杨氏模量等参数。

从图1中可以看出:后续信号处理是此系统的关键部分。因此，针对此SAW检测系统，设计了一种新颖锁相放大器，从理论分析与仿真结果可以看出:系统的信噪比得到了极大地提高，很好地抑制了噪声信号对SAW信号的影响。

2 信号处理单元

2.1 传统锁相处理单元

锁相放大器主要是由输入通道、参考通道和相关器三部分组成［14，15］，其电路框图如图 2 所示。

图2 传统锁相放大器原理图Fig 2 Principle diagram of traditional lock-in-amplifier

去噪原理的前提是输入信号的载波信号与参考信号（即检测光束的驱动信号）频率一致，对两信号进行乘法运算，并进行积分运算，根据信号相关原理，随积分时间的增大，不相关函数会逐渐趋于零。因为噪声信号是随机的，不具有一定的规律，因此，在积分时间足够大时，噪声信号的相关函数迅速衰减，而有用信号是周期函数，衰减较小，从而能有效地抑制噪声信号，并将有用信号从噪声中提取出来。

设输入信号为x（t），可描述如下

其中，第一部分为有用信号，即时刻τ时的信号，Aτ为τ时刻的信号幅值，ω0为信号的角频率，φ0为初相位，第二部分为各种频率噪声信号的表达式。

经过前置低通滤波器后，去除了部分低频信号，信号为

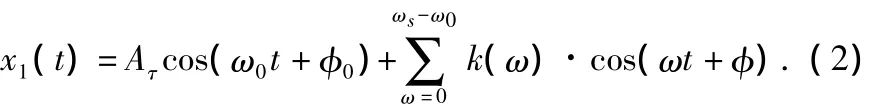
其中，ωs为噪声信号的频率，只有|ωs－ω0|＜LPF（前置低通滤波器）的等效噪声带宽的噪声能够通过前置低通滤波器。

设参考信号，即声光调制器的驱动信号为y（t），幅值为B，角频率与检测光束的驱动信号频率一致，为ω0，可描述如下

经过τ时刻的延时后，得到信号如下

经过乘法器的作用后，信号可描述如下

公式（5）所描述的就是经过乘法器后的信号，其中AτBcos（φ0－ω0τ）/2代表所要测量的检测信号幅值，然而，在解调过程中，信号会发生一定的频移，因此，解调后，可粗略的将噪声分为三组，如公式中所示:第一组为载波频率的高次谐波;第二组为载波和噪声的和频频信号;第三组分为两部分，即载波与噪声差频高于后置滤波器截止频率部分和差频低于后置滤波器截止频率部分。因为第一组和第二组的信号频率很高，因此，很容易被后置滤波器抑制，它们对信号质量的影响很小。第三组差频高于后置滤波器的截止频率部分，通过慎重地选择滤波器也可以得到很好的抑制，但其中差频低于后置滤波器截止频率部分，因为信号频率较低，再者滤波器的滤波能力也是有限的，不可能将通带与阻带之间做的很窄，因此，此部分噪声很难从信号中去除，成了过渡带最大的污染源。

通过后置滤波器的信号可描述如下

从公式中可以看出:噪声信号与SAW信号频率非常接近，为了更好地抑制噪声，提高测量系统的灵敏度，关键在于寻求一种能够排除与载波信号频率接近的信号的方法，显然，对于传统的锁相放大器来说，这一点很难做到。

2.2 新型锁相处理单元

实验过程中观测到，LG/LD-SAW方法所激发出的SAW信号幅值可达到2 V以上，而大部分噪声信号的幅值在0.2 V以下，针对此点，本文设计了一种新型的锁相放大器，在前置低通滤波单元前引入一去噪单元，滤除大部分的噪声信号，与以往锁相放大器不同的是，本设计还将前置放大器替换为电压跟随器［16］，其具有缓冲、隔离、提高带载能力等优点，从而达到前级电路与后级电路的阻抗匹配，又因为SAW信号带宽较宽，此处如果对输入信号进行放大的话，根据增益带宽积一定的原则［17］，会使得带宽缩小，造成失真。因此，利用去噪单元加电压跟随器的方法，可以将SAW直接送入前置低通滤波器进行处理，其结构如图3所示。

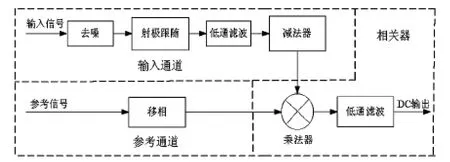
图3 新型锁相放大器原理图Fig 3 Principle diagram of the novel lock-in amplifier

此设计中的去噪单元可描述如下

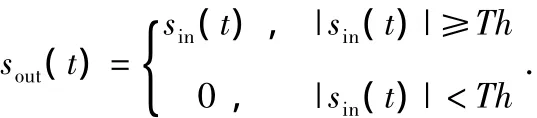
其中，sin（t）代表输入信号，sout（t）代表去噪单元的输出，Th为去噪单元的阈值。如公式（8）所述，只有高于阈值的信号才能通过此去噪单元，而低于阈值的信号输出为0，考虑到大部分噪声信号的幅值不超过0.2 V，本设计中的去噪单元包含正向导通电压为0.2 V的二极管阵列，限制±0.2 V以内的信号，从而在信号进入处理单元前，就去除了大部分噪声。

3 实验结果

本设计条件下，激光脉冲频率设定为为1 kHz，参考驱动信号为100 Hz。图4所示为实验中没有输入信号的情况下，光电探测器的输出信号，即微弱信号处理电路的输入信号，从图中可知，大部分信号噪声信号的幅度在±0.2V以内，因此，通过去噪单元后，剔除了大部分噪声信号。

图4 实验中的噪声信号Fig 4 Noise signal in the experiment

图5（a）所示为传统锁相放大器和新颖锁相放大器的输入信号的频谱，图5（b）为新颖锁相放大器经过去噪单元的频谱图，从图中可以明显地看出:去噪单元的应用，极大地削弱了噪声信号，当然，与此同时也会带来负面的影响，比如:引入一些高次谐波与噪声，这是不希望看到的。然而，通过观察输出信号频谱，可以明显的看出:所引入的噪声信号的频率远离载波信号的频率，差频较大，通过选择适当的后置低通滤波器，很容易将这些高频谐波从信号中移除，从而有效地抑制噪声。

经过传统锁相放大器后的波形与频谱如图6（a）、图6（b）所示。

通过理论与仿真分析，此信号处理单元的输出应该是一直流信号，但从图6（a）可以明显的看出:输出信号不能达到以稳定状态，其中仍含有部分噪声信号，大约0.3 V，信噪比大约为5。但是，如图6（b）所示，经过一定时间后，系统输出可达到一稳定状态，其中所含噪声小于0.003 V，信噪比大约460。

因此，通过对比可知，此新型锁相放大单元的去噪能力得到了明显的提高，信噪比提升了近100倍。

4 结论

通过对传统锁相放大器与本设计新型锁相放大器结果分析，能够更加准确地检测此系统的输出信号，而且能够达到更好的信噪比。本设计的新颖之处在于去噪单元中二极管对阵列的应用，从而在信号进入微弱信号处理单元之前，剔除大部分的噪声，大大提高了整套系统的检测精度。

图5 去噪单元前（a）后（b）的频谱Fig 5 Spectrum before and after the noise-removal block

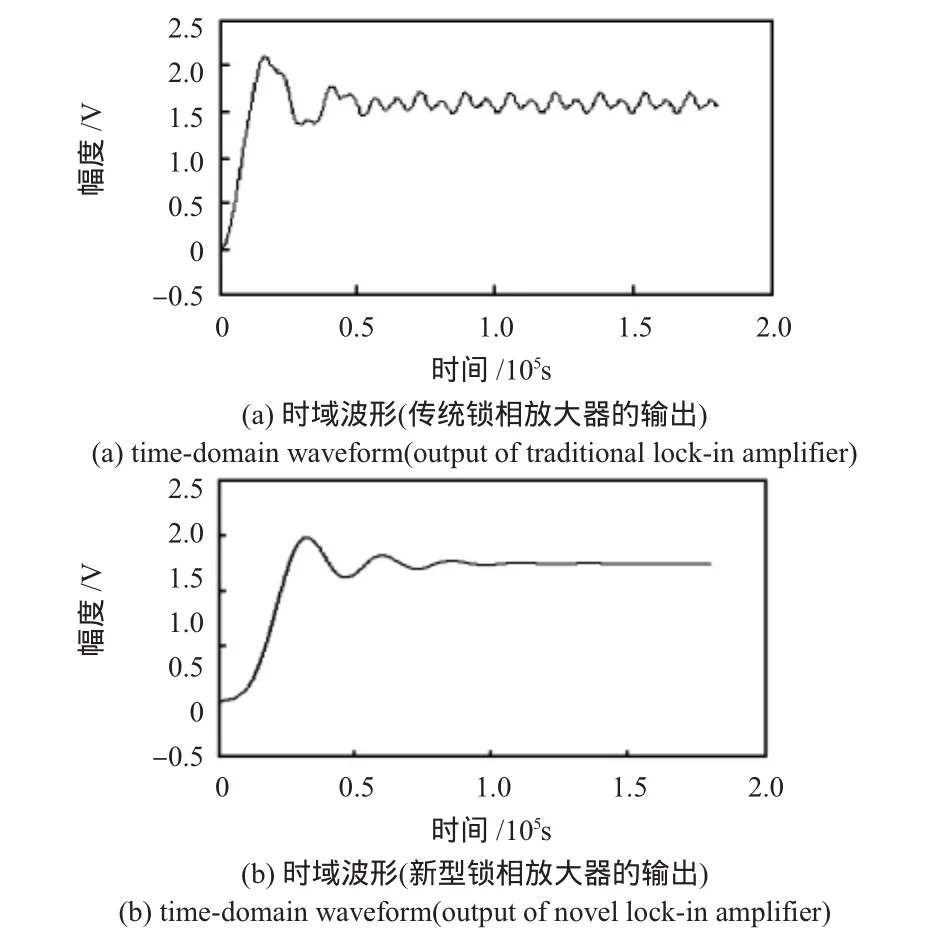
图6 传统锁相放大器与新型锁相放大器的输出Fig 6 Output of a traditional and the novel lock-in amplifier

［1］Spearing S M.Materials issues in micro-electro-mechanical systems（MEMS）［J］.Acta Materialia，2000，48（1）:179 －196.

［2］Tarui Y，Hirai T，Teramoto K，et al.Application of the ferroelectric materials to ULSI memories［J］.Applied Surface Science，1997，113 －114:656 －663.

［3］Maznev A A，Nelson K A，J.Rogers A.Optical heterodyne detection of laser-induced gratings［J］.Opt Lett，1998，23（16）:1319－1321.

［4］Duggal A R，Rogers J A，Nelson K A.Real time optical characterization of surface acoustic modes of polyimide thin film coatings［J］.Journal of Applied Physics，1992，72（7）:2823 －2839.

［5］Kitazawa Si，Putra T Y S P，Sakai S，et al.Laser detection of surface acoustic waves as a method of measuring an Ar ion beam modification of carbon thin film［J］.Nuclear Instruments and Methods in Physics Research Section B:Beam Interactions with Materials and Atoms，2003，206:952 －955.

［6］Hurley D C，Tewary V K，Richards A J.Thin-film elastic-property measurements with laser-ultrasonic SAW spectrometry［J］.Thin Solid Films，2001，398 －399:326 －330.

［7］Jalili N，Laxminarayana K.A review of atomic force microscopy imaging systems:Application to molecular metrology and biological sciences［J］.Mechatronics，2004，14（8）:907 －945.

［8］Flannery C M，Murray C，Streiter I，et al.Characterization of thinfilm aerogel porosity and stiffness with laser-generated surface acoustic waves［J］.Thin Solid Films，2001，388（1 －2）:1 －4.

［9］Passeri D，Bettucci A，Germano M，et al.Local indentation modulus characterization via two contact resonance frequencies atomic force acoustic microscopy［J］.Microelectronic Engineering，2007，84（3）:490 －494.

［10］Shintani K，Yanagitani T，Matsukawa M，et al.Non-destructive evaluation of thin ZnO shear wave transducer by Brillouin scattering［C］//Ultrasonics Symposium，2004 IEEE，2004:1864 －1867.

［11］Xiao X，You X，Yao S.Theoretical study of mechanical properties of multi-layer ULSI interconnect dielectrics by surface acoustic wave method［J］.Microelectronics Journal，2006，37（10）:1052－1055.

［12］Lee Y C，Bretz K C，Wise F W，et al.Picosecond acoustic measurements of longitudinal wave velocity of submicron polymer films［J］.Applied Physics，2009，69（12）:1692 － 1694.

［13］Bartels A，Hudert F，Janke C，et al.Femtosecond time-resolved optical pump-probe spectroscopy at kilohertz-scan-rates over nanosecond-time-delays without mechanical delay line［J］.Applied Physics，2006，88（4）:1117 －1 －1117 －3.

［14］高晋占.微弱信号检测［M］.北京:清华大学出版社，2004:154－174.

［15］刘 俊，张斌珍.微弱信号检测技术［M］.北京:电子工业出版社，2005:75－93.

［16］Bai M S.A novel faint signal processing method for sensitivity improvement of pump/probe-based LG/LD SAW spectroscopy system［J］.Nanomanufacturing，2011，301 －303:188 －194.

［17］赛尔吉欧·佛朗哥［美］.基于运算放大器和集成电路的电路设计［M］.刘树棠，荣 玫，等.译.西安:西安交通大学出版社，2010:229－236.