基于捷联惯导系统的杆臂效应误差分析
2012-07-25李鹏飞奔粤阳
李鹏飞,奔粤阳,张 亚,孙 骞
(1.海军装备部舰艇部,北京 100841;2.哈尔滨工程大学自动化学院,黑龙江哈尔滨 150001)
0 引言
惯性导航是20世纪发展起来的一种导航方法,它利用惯性元件测量载体的运动加速度和角速度,以此推算出载体的速度、位置和姿态,它是一种不依赖于任何外界信息,也不向外辐射能量的自主式导航系统。通常惯性导航系统(inertial navigation system,INS)可以分为两类:平台式惯性导航系统和捷联式惯性导航系统(strapdown inertial navigation system,SINS)。由于SINS的一系列优点,它的应用越来越广泛[1]。现代战争要求武器装备具有快速反应能力和精确打击能力,而武器装备的反应时间则主要取决于武器装备中的INS的初始对准时间。传统的自主式初始对准方式有很大的局限性,很难适用于现代战争的需要[2]。而传递对准是新一代快速反应、机动发射武器系统的关键技术,它的成功应用可以极大地提高武器系统的反应速度和防区外攻击能力。现代战争要求在保持武器系统战斗能力和可靠性的条件下,降低武器系统的成本[3]。因此,研究SINS的传递对准具有重要的实战意义。
速度匹配传递对准方法是目前最常用的、最成熟的一种传递对准方法,所以,本文以速度匹配传递对准为例进行分析。它是以速度差为观测量的,而杆臂效应误差是速度匹配传递对准方法中最主要的误差,本文对杆臂效应误差的基本原理进行了推导,并对其影响进行了分析。
1 速度匹配传递对准方法
文献[3,4]已经详细推导出了速度匹配传递对准中速度误差微分方程、失准角微分方程和惯性器件误差模型,在此不再赘述。速度匹配传递对准的状态方程为
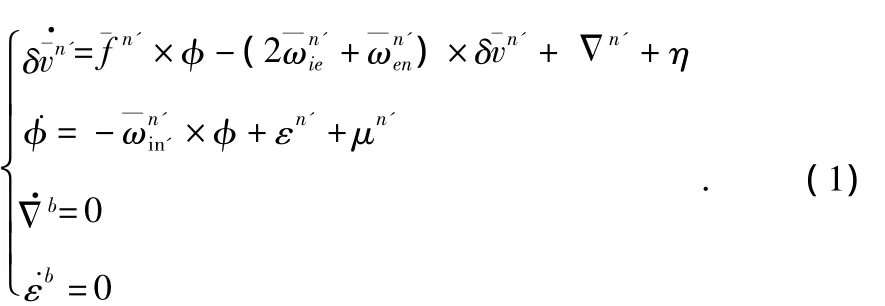
速度匹配传递对准以主子惯导间的速度差作为观测量,因此,得到速度匹配的滤波模型如下

式中X为系统的状态变量,且

式中W为系统噪声,且W=[ωaxωayωazωεxωεyωεz0 0 0 0 0]T,其中,ωax,ωay,ωaz为加速度计零偏随机白噪声,ωεx,ωεy,ωεz为陀螺仪漂移随机白噪声。
2 杆臂效应误差的基本原理
如图1所示,定义惯性坐标系为oixiyizi,载体坐标系为obxbybzb,并认为ob是载体的摇摆中心,在多数的研究中被认为是载体的重心,一般根据设计的载荷分布情况,求出重心位置,并且认为重心是固定的,且常假设主惯导安装位置与ob重合,子惯导的加速度计安装在载体坐标系中的固定点p为载体坐标系原点的位置矢量为p点相对于惯性坐标系原点的位置矢量为p点相对于载体坐标系原点的位置矢量[5,6]。

图1 安装位置示意图Fig 1 Diagram of installation position
由文献[5]可推证得出

理想情况下安装点应该在载体的摇摆中心,即rp=0,这样就不存在杆臂效应。在传递对准中认为主惯导安装在载体的摇摆中心,而子惯导通常并不能满足这样的要求,在实际运用中杆臂效应通常是不可忽略的。式(3)中的后面两项就是由于杆臂效应引起的子惯导敏感到而主惯导没有敏感到的杆臂加速度基本表达式[6]
由于

若定义表示杆臂加速度,则杆臂效应误差的基本方程为
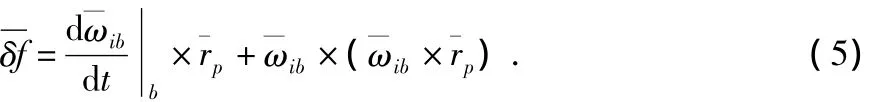
3 实验与分析
3.1 仿真实验与分析
下面通过仿真来分析杆臂效应误差的影响。

图2 杆臂效应加速度曲线Fig 2 Curve of the lever-arm effect acceleration
速度匹配传递对准中,存在这样的杆臂效应加速度与不存在杆臂效应时的对比曲线如图3所示。

图3 速度匹配失准角估计误差对比曲线Fig 3 Comparison curve of the estimation error of the velocity matching misalignment angles
根据图3发现失准角估计误差曲线有很大的波动,在很长时间内都没有收敛,而且估计误差很大,在200 s时,航向失准角估计误差为-0.5°。因此可以看出:杆臂效应误差对失准角估计误差影响很大。
3.2 实船实验与分析
如图4所示,本实验采用实验室自研光纤陀螺SINS进行某地系泊实船实验,来验证杆臂效应误差对失准角的影响。
其中,1为实验室自研光纤捷联惯导系统,1 513系统;2,3,4为数据采集系统(计算机);5为实验室自研光纤捷联惯导系统,1507系统;6为PHINS INS。

图4 船载实验设备安装示意图Fig 4 Installation diagram of the ship’s experimental equipment
本实验以法国IXSEA公司的PHINS导航系统作为姿态基准,将光纤陀螺惯导系统解算出的姿态信息与其进行对比,可以得到系统未经杆臂效应误差补偿时的失准角误差,如图5所示。

图5 实船实验存在杆臂效应时失准角误差曲线Fig 5 The ship’s experiment curve of the misalignment angles error while lever-arm effect exists
由上图可以看出:横滚、俯仰角和航向失准角误差收敛时间比较长,基本上在500s以后才开始收敛,而且,在500 s时失准角误差仍然很大,误差值分别为 -0.22°,-0.37°,-0.35°。所以,杆臂效应误差的存在会严重影响系统失准角的解算,从而会降低INS的导航精度。
4 结论
本文详细推导了速度匹配传递对准方法的速度误差微分方程、失准角微分方程、惯性器件微分方程和速度匹配滤波模型。在此基础上,介绍了杆臂效应产生的基本原理,并通过仿真图形可以看出:存在杆臂效应时失准角估计误差曲线的波动比较明显,并且,航向失准角估计误差稳态值为0.5°,验证了杆臂效应误差对失准角估计误差的影响。最后,对杆臂效应现象进行了实船实验,通过实船实验数据的分析,俯仰、横滚和航向的失准角估计误差分别为 -0.22°,-0.37°,-0.35°,从而验证了杆臂效应误差对失准角的影响。根据仿真和实验得出,杆臂效应误差会对失准角的估计产生影响。若要提高SINS的精度,必须采取一定的措施,消除或者减小杆臂效应误差的影响。
[1]陈 哲.捷联惯导系统原理[M].北京:宇航出版社,1986:1-9.
[2]刘 毅,刘志俭.捷联惯性导航系统传递对准技术研究现状及发展趋势[J].航天控制,2004,22(5):51 -55.
[3]李良君.传递对准误差补偿及精度评估方法研究[D].哈尔滨:哈尔滨工程大学,2008.
[4]戴邵武,李 娟,戴洪德,等.一种快速传递对准方法的误差模型研究[J].宇航学报,2009,30(3):942 -946.
[5]江 红,张炎华,赵忠华.捷联惯性导航系统传递对准的杆臂效应分析[J].中国造船,2006(4):71-75.
[6]何秀凤,袁 信.平台惯导系统中杆臂效应误差的研究与分析[J].航天控制,1995(2):22-30.
