一种新的LMS自适应滤波算法分析仿真研究
2012-07-25贺洪江王春霞
贺洪江,王春霞
(河北工程大学信息与电气工程学院,河北邯郸 056038)
0 引言
最小均方(LMS)算法是由Widrow和Hoff两人在1960年提出的,由于其计算复杂度低、易于实现等优点[1],广泛应用于自适应控制、系统辨识、信号处理和噪声抵消等领域,同时自适应滤波器在通信、雷达、工业控制、地震预报及生物医学电子学等领域也已经有了越来越广泛的应用。初始收敛速度、对时变系统跟踪能力、稳态误差以及抗噪声干扰能力是衡量LMS算法优劣的重要性能指标[2,3]。传统LMS算法中固定步长的取值不同会影响算法的性能。减小步长取值可以降低稳态误差,但会降低算法的收敛速度和对时变系统的跟踪能力;增大步长取值可以提高收敛速度,但会增大稳态误差。传统的固定步长的LMS算法的大收敛速度和小稳态误差不能同时满足,这就要求在收敛速度和稳态误差2个性能指标之间权衡。为此,人们提出了多种变步长 LMS 自适应滤波算法[3~10]。
文献[4]中提出的SVSLMS算法的收敛速度较快,但在自适应稳态阶段的步长变化较大,稳态误差也较大。文献[5]中提出的G-SVSLMS算法是在SVSLMS的基础上进行了改进,稳态步长变化比较缓慢,收敛速度也较快。文献[6]提出一种新的变步长函数,具有在初始阶段和未知系统时变时步长自动增大而在稳态时步长很小的特点,但收敛速度需要进一步提高。SVSLMS和G-SVSLMS算法的步长受误差调节,抗噪声能力比较低。
本文算法采用输入信号与误差信号不相关的特点,用误差信号的自相关时间均值来调节步长,并用绝对估计误差的扰动量以更新自适应滤波器的抽头向量,算法性能较上述算法有较大的优越性。
1 自适应滤波算法原理
LMS算法的基本原理是基于最速下降法,即沿着权值的梯度估值的负方向搜索,达到权值最优,实现滤波器的输出信号与期望输出信号之间的LMS误差。自适应滤波的原理框图[7]如图1所示。

图1 自适应滤波器原理框图Fig 1 Principle diagram of adaptive filter
图1中,x(n)为n时刻的输入信号矢量;y(n)为输出信号;v(n)为噪声信号;d(n)为期望输出信号;e(n)为d(n)和y(n)之间的误差信号估计;通过误差信号e(n)调节自适应滤波器抽头权向量,使自适应滤波器收敛至稳定状态。基于最速下降法的LMS算法公式[8]如下
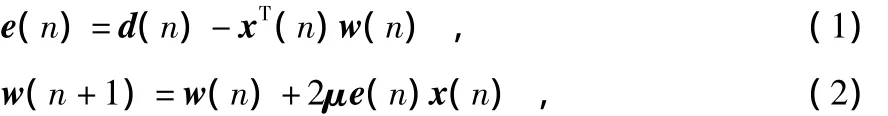
式中w(n)为n时刻N阶自适应滤波器的权系数;μ为控制稳定性和收敛性能的参量即步长因子。LMS算法收敛时,步长因子μ的取值范围为:0<μ<1/λmax,λmax为输入信号自相关矩阵的最大特征值。
2 新的变步长LMS算法与性能分析
变步长LMS算法的基本思想[9,10]是:在初始收敛阶段或者系统参数发生时变的时候,最优权值与自适应滤波器的权值相距较远,为了保证能有较快的收敛速度和对时变系统的跟踪速度,选取较大的步长μ;在算法接近收敛时,滤波器的权值接近最优权值,为了减少算法的稳态误差,选取较小的步长μ。基于这种思想,本文在前人研究的基础上,通过在步长参数μ(n)与误差信号e(n)之间建立一种新的非线性函数关系来调节步长,提出一种新的变步长LMS算法,本文算法步长因子函数和权系数更新公式如下

式中α为控制函数形状的常数,决定曲线上升的快慢;β为控制函数取值范围的常数。α,β分别变化时步长因子μ(n)和误差e(n)的关系曲线如图2和图3所示。

图2 α=1,β变化时μ(n)与e(n)的关系曲线Fig 2 Relation curves with μ(n)and e(n)when α =1 and different β

图3 β=1,α变化时μ(n)与e(n)的关系曲线Fig 3 Relation curves with μ(n)and e(n)when β =1 and different α
由图2可知,当α固定时,β取值越大,步长初始值也越大,收敛速度也越快,同时稳态误差也越大;β取值越小,步长初始值也越小,收敛速度也越慢,稳态误差也越小。由图3可知,当β固定时,α取值变化时也具有同样的特点,同时,在|e(n)|>1.3时步长变化不明显,但α越大时步长也越大,收敛速度也越快。e(n)趋近于0时,步长变化也较缓慢。由以上分析可知,新算法稳态时步长变化平滑,克服了SVSLMS算法e(n)接近0时步长变化太大的缺点。算法性能由α和β共同决定,当要求较快的收敛速度时,2个参数的取值都应该较大,当要求较小的稳态误差时,2个参数的取值都应该较小,在实际应用中根据环境的不同来确定最佳取值。
式(4)中的kγ(n)(|e(n)|-|e(n-1)|)为本文算法绝对估计误差的扰动量。传统算法采用随机梯度调整抽头权向量,每次迭代时的估计误差e(n)的正负并不确定,抽头权向量的调整只能围绕w0震荡。本文用绝对估计误差能更好地表示估计信号偏离期望信号的程度,扰动量可以对w(n)进行正反向调节来加快算法的初始收敛速度。通过γ(n)扰动量幅度因子,把扰动量对w(n)的调节控制在一个最佳水平。γ(n)以式(5)的指数形式衰减,其中,p<1。在迭代次数比较少时,扰动量对w(n)的影响较大,随着迭代次数的增加,γ(n)趋近于0,e(n)的波动几乎不会对w(n)造成影响,从而使稳态误差抑制在较低的水平。为了加强算法的抗噪性能,本文算法中用式(3)的误差向量自相关值e(n)e(n-1)来调节步长。设自适应滤波器抽头权向量的维纳解为w0,令Δw=w(n)-w0为n时刻权系数矢量与最佳值之差,期望信号的介入噪声为ξ(n),与x(n)不相关,则有
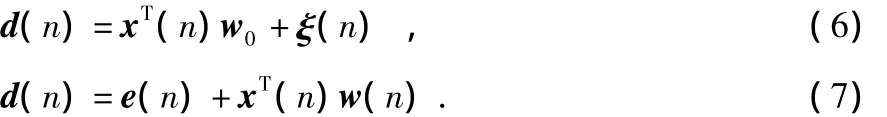
由式(6)、式(7)得
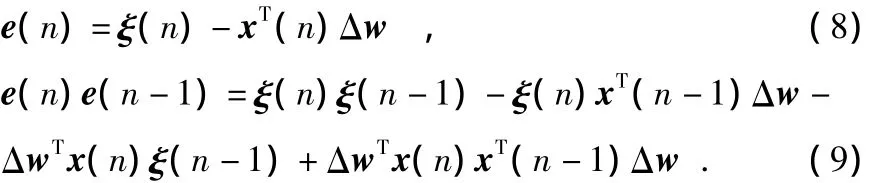
设噪声功率为σ2,由系统特性可知
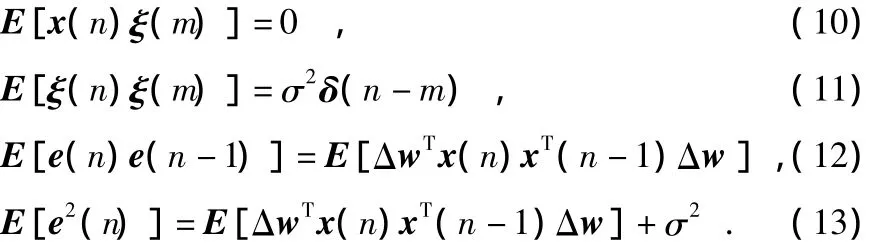
由式(12)和式(13)可知,误差自相关函数只与输入信号有关,而与噪声无关。SVSLMS算法用误差调节步长,GSVSLMS算法用误差功率调节步长,导致在低信噪比条件下性能恶化。本文算法的噪声抑制能力优于上述算法。
3 算法仿真结果分析比较
3.1 仿真条件
1)自适应滤波器阶数L=2;
2)未知系统的 FIR 系数为w1=[0.8,0.5]T;
3)参考输入信号x(n)是均值为0,方差为1的高斯白噪声;
4)v(n)为与x(n)不相关的高斯白噪声,其均值为0,方差为1;
5)在本文实验条件下对三种算法进行了大量的仿真,测定了三种算法性能最优时的参数取值范围,参数取值如下:SVSLMS算法中α=150,β=0.07;G-SVSLMS算法中α=450,β=0.06;本文算法中α=1500,β=0.05,γ(0)=0.4,p=0.4;
6)采样点数为1000,分别做500次独立仿真,然后通过求其统计平均,得出学习曲线。
3.2 仿真结果分析比较
本文算法和SVSLMS算法及G-SVSLMS算法收敛曲线的比较如图4所示。
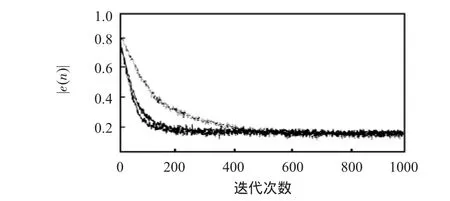
图4 三种不同算法收敛曲线Fig 4 Convergence curve of three different algorithm
图4中的三条收敛曲线从上到下依次为SVSLMS算法、G-SVSLMS算法和本文算法的收敛曲线。由图3可知,本文算法的收敛速度快于SVSLMS算法和G-SVSLMS算法,稳态误差小于SVSLMS算法和G-SVSLMS算法的稳态均方误差较接近,本文算法有效抑制了随机噪声对信号的干扰,在综合性能上优于SVSLMS算法和G-SVSLMS算法,验证了前文对算法性能的分析。
4 系统发生时变时算法分析
系统发生时变时的总采样点数为1000,系统在第500个采样点时刻未知系统发生时变,未知系统的FIR系数由原来的w1=[0.8,0.5]T变为w2=[0.7,0.5,0.2]T,做500次独立仿真,求其统计平均,得出系统发生时变时本文算法收敛曲线如图5所示。

图5 本文算法发生时变时收敛曲线Fig 5 Convergence curve when this algorithm have time-varying
由图可以看出:本文算法在系统发生时变时同样具有很快的收敛速度,因此,本文算法在综合性能上优于SVSLMS算法和G-SVSLMS算法的同时仍具有较好地对时变系统的跟踪能力。
5 结论
本文通过在步长因子与误差信号之间建立一种新的非线性函数数,同时引入绝对估计的扰动量,提出了一种新的变步长LMS自适应滤波算法,较好地解决了收敛速度和稳态误差之间的矛盾。理论分析与仿真验证显示,本文算法不仅初始收敛速度、稳态误差和抗噪性能均优于传统的几种算法,而且具有较好的对时变系统的跟踪能力。
[1]Diniz P S R.自适应滤波算法与实现[M].刘郁林,译.北京:电子工业出版社,2004:48.
[2]Diniz P S R.Adaptive filtering:Algorithms and practical implementation[M].2nd ed.USA:Spring,2002.
[3]叶水生,余荣贵,吴 霄,等.一种新的自适应最小均方算法及其应用研究[J].电测与仪表,2008,45(511):9.
[4]覃景繁,欧阳景正.一种新的变步长自适应滤波算法[J].数据采集与处理,1997,12(3):171 -174.
[5]高 鹰,谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报,2001,29(8):1094 -1097.
[6]李方伟,张 浩.一种新的变步长LMS自适应滤波算法及其仿真[J].重庆邮电大学学报:自然科学版,2009,21(5):591-594.
[7]Irusta U,Ruiz de G S,Ruiz J,et al.A variable step size LMS algorithm for the suppression of the CPR artifact from a VF signal[J].Computers in Cardiology,2005,48(4):179 -182.
[8]Mohammad Z U R,Ahamed S R,Koti R D V R.Cancellation of artifacts in ECG signals using sign based normalized adaptive filtering technique[C]//2009 IEEE Symposium on Industrial Electronics and Applications,ISIEA 2009,Kuala Lumpur,Malaysia,2009:442- 445.
[9]罗小东,贾振红,王 强.一种新的变步长LMS自适应滤波算法[J].电子学报,2006,34(6):1123 -1126.
[10]Givens M.Enhanced convergence normalized LMS algorithm[J].IEEE Signal Processing Magazine,2009,26(3):81 -95.
