基于半方差函数的海杂波长相关特征分析
2012-07-25朱晓华
孙 康 金 钢 朱晓华
①(南京理工大学电子工程与光电技术学院 南京 210094)
②(中国空气动力研究与发展中心 绵阳 621000)
③(电子科技大学自动化工程学院 成都 611731)
1 引言
自20世纪70年代以来,分形理论逐渐被应用到雷达海上目标探测,成为对海杂波特性有效描述的一种新手段,而寻找海杂波和目标信号的显著分形特征差异用以实现目标识别一直都是该领域关注的一个焦点[1-2]。有研究表明,长相关性与尺度和分形有着密切的关系,分形自仿射过程通常会具有长相关特性,而长相关时间序列也会表现出自仿射性质[3-6]。迄今为止,已有许多方法用于对长相关的判断估计,典型的如重标极差(R/S)法、周期图法、去趋势波动分析(DFA)方法和小波方法等[7-9]。半方差函数是地质统计学用来分析数据空间关系的一个主要数学工具,Gallant和Mark等在地形学的分形研究中用其估计分形分维值[10,11]。同时,半方差函数也可用来测量自仿射时间序列的长相关性质,并且这种方法对于平稳时间序列和非平稳时间序列均有效[12]。
考虑到海杂波由于具有一定的分形特性,因此可能会表现出某些长相关特征,本文将半方差函数这一数学工具引入到对海杂波分形特征的研究分析,以寻求可能区分目标和海杂波的有效途径。通过对海杂波的半方差函数值在空间维上做归一化处理,可观察到归一化后的目标半方差函数曲线与海杂波半方差函数曲线无论在暂态区间还是稳态区间都存在着明显的差别,由此,可以分别用半方差曲线拟合斜率和半方差曲线样本均值作为区分目标和海杂波的分形特征值,用以进行海上小弱目标检测。
2 长相关特征与半方差函数
长相关表示了时间序列具有持续性,即如果前一个序列值大,通常紧接的后一个序列值也比较大,前一个序列值小,紧接的后一个序列值也比较小。如果时间序列的增量,即相邻序列值的差值构成的序列表现出长相关,那么原时间序列会具有自仿射性质。因此,长相关性质可以反映和刻画自仿射分形特征。
长相关,也称为长记忆,其通常的定义为:如果一个序列{Xt,t∈T}的自协方差函数γ(k)的绝对值之和发散,即

式中k表示时间间隔,也称为延迟,则该序列表现出长相关特性[13-15]。
长相关还可以用自相关函数来定义:设ρ(k)是一组观测值 {X1,X2,… ,Xn}的自相关函数,如果其满足以下条件:

其中cp是有限正常数,α∈ ( 0,1),则该过程是长相关的[16]。
半方差函数是一种测量长相关的方法,在地质统计学中用来分析数据空间关系。设f(M)是在几何区域V中M一点上有给定的几何支撑v定义的区域化变量值,一般来说v很小且被认为是点集。对于矢量自变量h,半方差函数γ(h)由下面的表达式定义:

因为样本之间离得越远,它们之间的属性度越不相同,所以一般来说,半方差函数是距离h的递增方程。它对一个样本的影响范围给出了一个较精确的内涵[17]。
特别地,对于离散时间序列{yn,n=1,2,…,N},定义
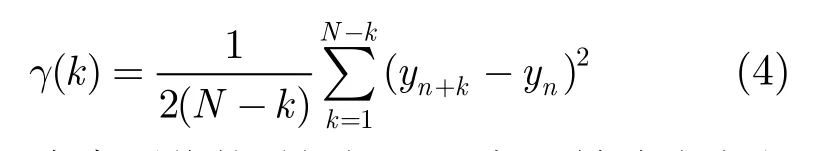
其中k是两个序列值的时间间隔,式(4)被称为半方差函数。处于时间间隔k的序列值之间越相似,半方差函数值γk越小;反之,γk越大,说明序列值之间的相似性越小[12,18]。
3 海杂波的长相关特征
本文使用的海杂波数据是加拿大 McMaster大学于1993年利用IPIX高分辨率雷达实地测量的海杂波数据[19]。目前提供的数据是在14个不同时间不同海洋环境下测量得到的,每次测量分别使用了 4种发射/接受极化方式,即2种同极化方式(HH, VV)和2种交叉极化方式(HV, VH),即有14×4组测量数据。每组测量数据包含14个不同距离单元,每个距离单元数据包含有217个样本点(采样频率1 kHz)。在14个距离单元中,一部分单元没有目标,另一部分有目标存在的单元又分为主要目标单元和次要目标单元,主要目标单元中雷达回波信号最强,毗邻主要目标单元的几个距离单元中目标也可能在雷达上可见,称为次要目标单元。
采用半方差函数对此海杂波实测数据进行分析,并以各距离单元的均值作为归一化系数,将得到的半方差函数值在空间维上进行归一化处理,得到的具有代表性的结果如图1所示。海杂波的半方差函数曲线提供了一种随时间间隔k变化的海杂波数据的相关结构的图形化描述,根据图形的曲线特征,可将图1的半方差曲线分成暂态区间(k<1 s)和稳态区间(k>1 s)两个部分,分别如图2和图3所示。
(1)在暂态区间中(图2),随着时间间隔的增大,目标的半方差函数曲线呈上升趋势,反映了目标信号的相关程度逐渐减弱;与之相反,海杂波的半方差函数曲线则缓慢下降,也即其相关程度缓慢增强。在时间间隔非常小的时候,目标与海杂波在时间上的相关程度虽然有差别,但是这种差别微乎其微。随着时间间隔的增大,其差别也增大。
可定义半方差曲线拟合斜率作为特征参数来表征这一特性:

图4为某次测量得到的不同距离单元上暂态区间的特征参数S值。可见,主要目标单元的S值显著大于非目标单元的S值,在特征参数曲线上形成一个明显的尖峰,且前者是正数,后者为负数。毗邻主要目标单元的次要目标单元中由于可能包含有部分目标信息,因此其S值也会高于无目标单元。
(2)在稳态区间中(图3),随着时间间隔的增加,目标和海杂波的半方差函数曲线都在一个比较小的区间内上下波动。相比之下,海杂波波动的幅度较小,而目标波动的幅度则明显大一些,同时,目标半方差函数值要远远大于海杂波的值。随着时间间隔的进一步加大,海杂波幅度值的强关联程度基本保持不变,而此时目标的弱关联程度也基本维持在某一个区间内,对此,可采用如下定义的半方差曲线样本均值加以描述:

其中L1和LN分别是稳态区间的起点和终点。采用式(6)定义的参数,典型的测量结果如图5所示,可以看到,主要目标单元的E参数值要远大于海杂波单元的E参数值。
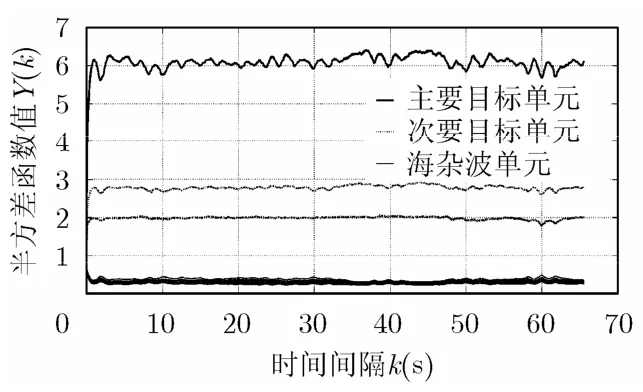
图1 一组海杂波和目标的半方差函数曲线
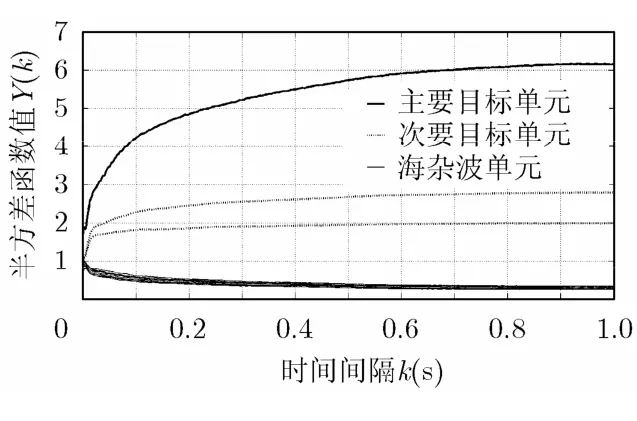
图2 暂态区间的海杂波和 目标的半方差函数曲线
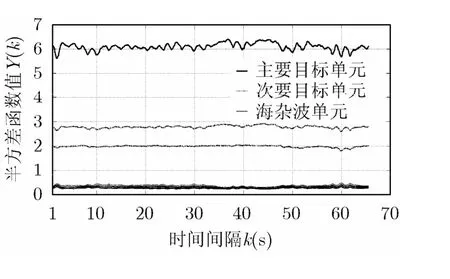
图3 稳态区间的海杂波和 目标的半方差函数曲线

图4 一组海杂波的14个距离单元的曲线暂态区间拟合斜率值
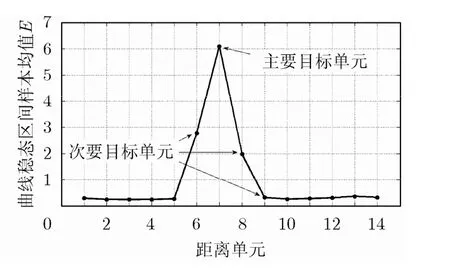
图5 一组海杂波的14个距离单元的曲线稳态区间样本均值
图6和图7分别是4种发射/接受极化形式下的两种特征参数估计结果,可见主要目标单元和无目标单元可被有效区分,在主要目标单元处,参数曲线有一个明显的峰值。对所有各组测量数据均有此同样结果。进一步分析比较可知,在4种极化方式中,交叉极化(HV和VH极化)的区分效果比较显著和稳健,而在同极化情况下(HH和VV极化),主要目标单元处的峰值有一些起伏。部分情况下,当HH极化下峰值较大时,VV极化下的峰值则会较低,反之亦然。
4 结束语
本文利用半方差函数分析海杂波的长相关特性,对于所获得的特征曲线,将其分为暂态区间和稳态区间两部分,目标和海杂波在这两个部分中均表现出各自明显不同的关联特性,根据这些特性提出了以半方差曲线拟合斜率和半方差曲线样本均值,分别作为描述海杂波暂态与稳态区间长相关特性的特征参数。仿真分析试验结果表明,基于这两种特征参数可以将目标和海杂波有效区分开来。

图6 4种发射/接受极化形式下的半方差曲线拟合斜率值
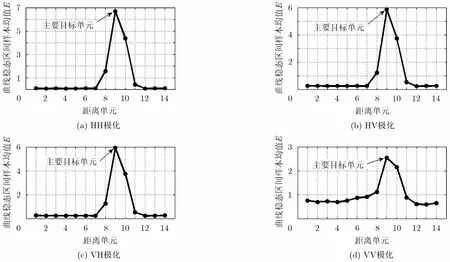
图7 4种发射/接受极化形式下的半方差曲线样本均值
[1]陈小龙, 刘宁波, 宋杰, 等. 海杂波FRFT域分形特征判别及动目标检测方法[J]. 电子与信息学报, 2011, 33(4): 823-830.
Chen Xiao-long, Liu Ning-bo, Song Jie,et al.. Fractal feature discriminant of sea clutter in FRFT domain and moving target detection algorithm[J].Journal of Electronics&Information Technology, 2011, 33(4): 823-830.
[2]刘宁波, 黄勇, 关键, 等. 实测海杂波频域分形特性分析[J].电子与信息学报, 2012, 34(4): 929-935.
Liu Ning-bo, Huang Yong, Guan Jian,et al.. Fractal analysis of real sea clutter in frequency domain[J].Journal of Electronics&Information Technology, 2012, 34(4): 929-935.
[3]Samorodnitsky G. Long range dependence[J].Foundations and Trends in Stochastic Systems, 2006, 1(3): 163-257.
[4]Meyers R A, Eigen M, Lauterbur P,et al.. Encyclopedia of Complexity and Systems Science[M]. New York:SpringerScience+BuisinessMedia, LLC., 2009: 3754-3778.
[5]Karagiannis T, Faloutsos M, and Riedi R H. Long-range dependence: now you see it, now you don't![C]. IEEE Global Telecommunications Conference, Taipei, 2002, 3: 2165-2169.
[6]Sun Wei, Rachev S, and Fabozzi F J.Fractals or I.I.D.:evidence of long-range dependence and heavy tailedness from modeling German equity market returns[J].Journal of Economics and Business, 2007, 59(6): 575-595.
[7]Fernandez V. Alternative estimators of long-range dependence[J].StudiesinNonlinearDynamics&Econometrics, 2011, 15(2): Artical 5.
[8]Power G J and Turvey C G. Long-range dependence in the volatility of commodity futures prices: wavelet-based evidence[J].Physica A:Statistical Mechanics and Its Applications, 2010, 389(1): 79-90.
[9]Abry P, Borgnat P, Ricciato F,et al.. Revisiting an old friend:on the observability of the relation between long range dependence and heavy tail[J].Telecommunication Systems,2010, 43(3/4): 147-165.
[10]Gallant J C, Moore I D, Hutchinson M F,et al.. Estimating fractal dimension of profiles: a comparison of methods[J].Mathematical Geology, 1994, 26(4): 455-481.
[11]Mark D M and Aronson P B. Scale-dependent fractal dimensions of topographic surfaces: an empirical investigation, with applications in geomorphology and computer mapping[J].Mathematical Geology, 1984, 16(7):671-683.
[12]Malamud B D and Turcotte D L. Self-affine time series:measures of weak and strong persistence[J].Journal of Statistical Planning and Inference, 1999, 80(1/2): 173-196.
[13]Cutler C D and Kaplan D T. Nonlinear Dynamics and Time Series: Building a Bridge between the Natural and Statistical Sciences[M]. Rhode Island: American Mathematical Society,2007: 153-160.
[14]Seese D, Weinhardt C, and Schlottmann F. Handbook on Information Technology in Finance[M]. Berlin, Heidelberg:Springer-Verlag Berlin Heidelberg, 2008, Chapter 23.
[15]Franzke L E, Graves T, Watkins N W,et al.. Robustness of estimators of long-range dependence and self-similarity under non-gaussianity[J].Philosophical Transactions of the Royal Society of London,Seiries A, 2012, 370(1962): 1250-1267.
[16]Beran J. Statistics for Long-Memory Processes[M]. New York:Chapman & Hall, 1994, Chapter 2.
[17]Matheron G. Principles of geostatistics[J].Economic Geology,1963, 58(8): 1246-1266.
[18]Almeida J, Silva A, and Paiva A. Automatic eye detection using semivariogram function and support vector machine[C].17th International Conference on Systems, Signals and Image Processing, Niteroi, Brazil, 2010: 174-177.
[19]The McMaster IPIX radar sea clutter database[OL]. http://soma.crl.mcmaster.ca/ipix/. 2011.3.
