基于压缩感知的单通道鲁棒自适应波束形成算法

李洪涛 贺亚鹏 肖 瑶 朱晓华

(南京理工大学电子工程与光电技术学院 南京 210094)

1 引言

自适应波束形成算法在导向矢量和信号协方差矩阵精确已知的情况下，具有良好的性能，但在低快拍下或接收数据包含较强期望信号以及导向矢量存在误差时，会出现期望信号相消、旁瓣电平升高等鲁棒性问题。因此波束形成的鲁棒性得到了广泛的研究：基于对角加载(DL)的波束形成算法计算简单[1]，但其对角载入值需要正确估计；特征空间波束形成(ESB)算法[2,3]具有良好的性能，然而需要进行特征空间分解并正确估计其空间信号源数目；稍后提出的最差性能最优化(WCPO)算法[4,5]，鲁棒Capon波束形成(RCB)算法[6]，以及双约束鲁棒Capon波束形成(DCRCB)算法[7]等，经证明均属于对角加载类算法；基于二阶锥规划(SOCP)的鲁棒波束形成算法[8,9]通过在主瓣区域内形成平顶响应，对导向矢量误差具有良好的鲁棒性，但需要主瓣区域宽度的信息。

压缩感知[10-14](CS)理论被广泛应用于图像处理[15]、无线通信[16]以及雷达[17-22]等诸多工程领域。利用信号在空域的稀疏性[23,24]，文献[25]采用CS理论对阵列接收信号在时域内进行随机测量，减少阵列在时域的采样数，提出一种基于 CS的波束形成算法，但该算法要求阵列接收确定形式信号，且不能适用于相干性信号。

针对上述问题，本文提出一种新颖的基于 CS的单通道鲁棒自适应波束形成(CS-RAB)算法。首先提出一种单通道阵列体制，采用0/π移相器对每个阵元进行随机移相处理，经功分器后合为一路输出，进行低快拍空域随机采样，由此构建新的波束形成CS模型，其感知矩阵满足约束等容(RIP)条件，保证采用 CS重构算法进行波束形成的有效性和鲁棒性；在此基础之上，采用快速的鲁棒平滑L0 (RSL0)算法重构信号矩阵，最后以表征阵列鲁棒性的阵列灵敏度作为目标函数，以干扰矩阵作为约束条件，形成有效波束。CS-RAB算法只需一个射频通道，即可在低快拍且接收数据中包含较强期望信号的情况下对任意相干、非相干干扰信号进行有效抑制，并可避免因通道间不一致造成的鲁棒性问题、利于工程实现。

2 信号模型

2.1 单通道阵列模型

设射频单通道阵列如图1所示，由L个阵元组成，每个阵元均连接一个0/π移相器，然后通过功分器合为一路输出，再经过单路射频通道和A/D转换器后转换为数字信号yk输出，即

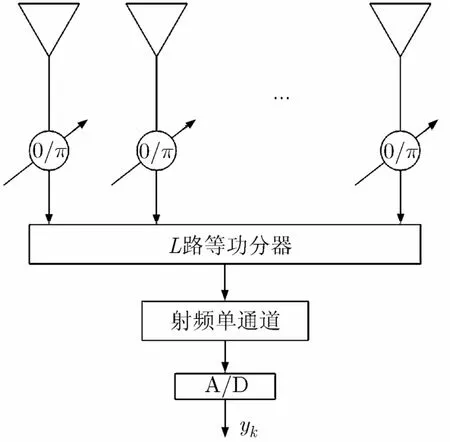
图1 单通道体制阵列模型

其中d= [d1,d2,···,dL]T为由0/π移相器生成的加权矢量，其元素di=cos(0/π) = ± 1,i= 1 ,2,… ,L,x为阵列输入信号，n为方差为σ2的高斯白噪声矢量。

单通道阵列由于只具有一个射频通道，因此具有成本低、体积小等优点，且可避免因通道间增益不一致、幅相不平衡等造成的鲁棒性问题，具有很强的工程应用价值。将CS理论运用于单通道阵列，利用0/π移相器随机相位变化实现空域随机采样，可在低快拍下有效恢复阵列各阵元相位与幅度信息，进行波束形成。

2.2 感知矩阵RIP条件分析

因为x在频域为K稀疏信号[24]，即

其中F为L×L维的傅里叶变换矩阵。由CS理论可知，仅需采用少量的阵元数和快拍数对x进行测量就可以完全恢复s。根据频域与空域的对称性，目标在空域内是稀疏的，由于目标信号的时间相关性[26]，设在N个快拍期间，目标未跨角度单元移动，则

将式(2)代入式(3)可得

其中D= [d1,d2,… ,dN]为经过0/π移相器N次随机变化相位生成的L×N维加权矢量矩阵，其元素为服从独立同分布的伯努利随机变量[21]，I为单位矩阵，w=Dn为L×1维的噪声矢量，z=Is,Φ=DF-1,Θ=ΦI，即z为稀疏基矩阵I下的稀疏信号，Φ为元素服从独立同分布的伯努利随机变量的随机噪声矩阵与标准正交基的乘积。

因此，采用射频单通道体制对空间信号进行接收采样可看作采用测量矩阵Φ对稀疏信号z进行随机测量，且感知矩阵Θ满足RIP条件，保证了采用CS重构算法进行波束形成的有效性和鲁棒性。

2.3 CS优化模型

根据CS理论，当阵元个数L≥0.28ln(N/K)[27]时，式(4)可通过求解在噪声环境下的 L0范数优化问题，得到空域目标信息

其中常量ε与噪声方差相关。该优化问题可采用基追踪去噪(BPDN)算法[28]、丹茨格估计器(DS)算法[29]、快速的RSL0[30,31]算法等进行求解，其中RSL0算法在相同的估计精度下，具有运算速度[30]较快的优点。

由于 L0范数是离散的，式(5)的最小化问题不能直接求解。为此，RSL0算法定义一个复函数：

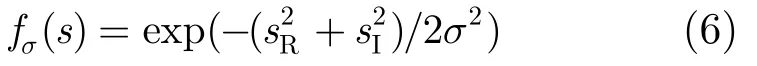
将式(7)代入式(5)，可得RSL0算法模型为

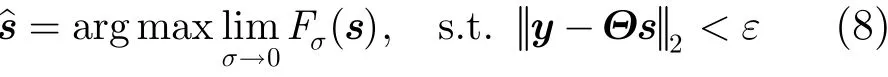
其中，为避免式(8)的解落入局部最优解，RSL0算法首先将σ初始化为一个足够大的值，然后将其衰减至足够小，通过在σ衰减过程中，求解在约束条件下目标函数最大值对应的σ逼近式(8)的最优解。

3 基于CS的鲁棒波束形成算法

由式(8)可得空间信号信息矩阵G为

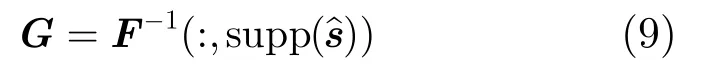
则空间信号的个数为

设a(θ0)为期望方向信号的导向矢量，则空间信号与期望信号的K×1维相关矢量B为

当训练数据中存在期望信号时，信号相关矢量B中必有一个元素为 1，其在信号相关矢量B中的位置对应矩阵G中期望信号的方向矢量，当训练数据中不含期望信号时，信号相关矢量B中所有的元素必然小于1。

用信号相关矢量B修正空间信号信息矩阵G，得到

其中1K为所有元素为1的K×1维矢量。

则为不包含期望信号信息的干扰信号信息矩阵，利用作为干扰抑制的约束条件，以表征阵列鲁棒性的阵列灵敏度[7]作为目标函数，提出CS-RAB算法。

利用 Lagrange乘子算法求解式(13)，可得CS-RAB算法的加权矢量为

4 计算机仿真分析

本节通过非相干干扰、相干干扰等多种信号模型，将CS-RAB算法与采样协方差矩阵求逆(SMI)算法、对角加载采样协方差矩阵求逆(LSMI)算法进行对比，验证算法的有效性。仿真中空间信号采样阵元个数L=16，阵元间距d=λ/2，快拍数为10。

实验1设空间存在两个非相干信号，入射角分别为-5°, 8°，信号的SNR均为10 dB。图2为CS-RAB算法空域谱估计的输出，其中虚线为信号实际方向。从图2中可以看出，CS-RAB算法可以精确估计出信号的位置，并对噪声进行有效地抑制，因此具有较低的旁瓣，平均达到-200 dB。

图2 非相干信号的空域谱估计输出

实验2设空间存在两个非相干干扰信号，其入射角分别为8°, -25°，期望信号方向为0°，输入信号SNR为30 dB。图3(a)为各算法在INR为10 dB时，输出方向图对比，其中p(θ)为归一化方向图。从图3(a)中可以看出，CS-RAB算法在训练数据中包含较强期望信号的情况下不仅可以对干扰形成零陷，且可以保持较低的旁瓣电平；SMI算法在快拍数小于阵元数以及训练数据中包含期望信号的情况下，已无法形成波束主瓣，性能严重下降；LSMI算法同样在较高的输入SNR下无法形成主瓣，且旁瓣电平较高，零陷深度小于CS-RAB算法。图3(b)为各算法在INR为30 dB时，输出波束方向图对比。从图3(b)中可以看出，CS-RAB算法仍可有效抑制干扰，SMI算法与LSMI算法性能则随着INR的增强，进一步恶化。

实验3设空间存在两个相干干扰信号，其入射角分别为30°, -20°，期望信号方向为0°，训练数据中无期望信号。图4(a)为各算法在INR为10 dB时输出方向图对比。从图4(a)中可以看出，CS-RAB算法可以对相干干扰形成零陷，且主瓣和旁瓣性能都较好；SMI算法以及LSMI算法均无法对相干干扰形成零陷，且旁瓣电平均高于CS-RAB算法。图4(b)为各算法在INR为30 dB时输出方向图对比。从图4(b)中可以看出，随着INR的增加，CS-RAB算法仍可有效抑制干扰，而SMI算法与LSMI算法的性能则进一步恶化。

实验4设空间存在两个非相干干扰信号，其入射角分别为20°, -8°，期望信号方向为0°，训练数据中无期望信号。设阵列通道间增益不一致，其各增益服从均值为1，方差为0.01的复高斯分布。图5(a)为各算法在INR为10 dB时输出方向图对比。从图5(a)中可以看出，SMI算法在通道间幅度不一致的情况下已经无法形成波束主瓣；LSMI算法由于进行了对角加载，因此可以形成有效波束主瓣，但无法准确抑制干扰；CS-RAB算法由于只有一个射频通道，因此可在形成波束主瓣同时，对干扰进行有效地抑制。图5(b)为各算法在INR为30 dB时输出方向图对比。从图5(b)中可以看出，随着INR的增加，SMI算法与LSMI算法的性能均有不同程度的下降，CS-RAB算法在高INR以及通道间幅度不一致的情况下，仍可形成波束主瓣，并有效抑制干扰。

实验5设空间存在两个非相干干扰信号，其入射角分别为10°, 20°，期望信号方向为0°，训练数据中无期望信号。图6为由RSL0算法恢复信号估计的干扰信号角度均方根误差随干扰INR变化的曲线；图7为阵列输出SINR随干扰INR的变化曲线。从图6可以看出，估计的干扰信号角度均方根误差随干扰INR的增加而快速减小，即干扰的INR越大，RSL0算法恢复信号的误差越小。从图7可以看出，本文提出的方法其阵列输出SINR随干扰INR的变化基本不变，即由于干扰INR较低引起的信号估计误差对波束形成基本没有影响。其实质性原因是在干扰INR较大的情况下，RSL0算法可以准确估计干扰位置，此时波束形成的零陷中心对准干扰，波束可有效抑制强干扰；在干扰INR较小的情况下，RSL0算法估计的干扰位置与实际干扰位置存在一定的偏差，波束形成的零陷中心未对准干扰，但由于估计的干扰信号角度误差并不大，干扰并未完全移出零陷，且干扰较弱，波束形成的零陷依然可对干扰进行有效抑制。

5 结论

图3 高信噪比下各算法方向图对比

图4 相干干扰下各算法方向图对比

图5 通道间幅度不一致情况下各算法方向图对比

图6 估计干扰信号均方根误差随INR的变化曲线

图7 阵列输出SINR随INR的变化曲线

针对存在相干干扰、训练数据中包含期望信号以及低快拍下自适应波束形成算法鲁棒性下降的问题，提出一种基于CS的单通道鲁棒波束形成算法。提出的单通道阵列体制具有成本低、体积小等优点，且可避免因通道间增益不一致、幅相不平衡等造成的鲁棒性问题，具有较强的工程应用价值。基于单通道阵列体制的 CS-RAB算法可在较高输入 SNR下有效抑制相干、非相干干扰信号，是一种适应性较强的鲁棒波束形成算法。

[1]Cox H, Zeskind R M, and Owen M M. Robust adaptive beamforming[J].IEEE Transactions on Acoustic, Speech and Signal Processing, 1987, 35(10): 1365-1376.

[2]Chang L and Yeh C C. Performance of DMI and eigenspace-based beamformers[J].IEEE Transactions on Antennas Propagation, 1992, 40(11): 1336-1347.

[3]Feldman D and Griffiths L. A projection approach for robust adaptive beamforming[J].IEEE Transactions on Signal Processing, 1994, 42(4): 867-876.

[4]Vorobyov S A, Gershman A B, and Luo Z Q. Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem[J].IEEE Transtions on Signal Processing, 2003, 51(2): 313-324.

[5]刘聪锋, 廖桂生. 最差性能最优通用信号模型稳健波束形成算法[J]. 电子学报, 2010, 38(6): 1249-1255.

Liu Cong-feng and Liao Gui-sheng. Robust beamforming algorithm for general signal models using worst-case performance optimization[J].Acta Electronica Sinica, 2010,38(6): 1249-1255.

[6]Li J, Stoica P, and Wang Z. On robust Capon beamforming and diagonal loading[J].IEEE Transactions on Signal Proessing, 2003, 51(7): 1702-1715.

[7]Li J, Stoica P, and Wang Z. Doubly constrained robust capon beamformer[J].IEEE Transactions on Signal Processing,2004, 52(9): 2407-2423.

[8]Zhu L Y, Ser W, Er M H,et al.. Robust adaptive beamformers based on worst-case optimization and constraints on magnitude response[J].IEEE Transactions on Signal Proessing, 2009, 57(7): 2615-2628.

[9]鄢社锋, 马远良. 传感器阵列波束优化设计[M]. 北京: 科学出版社, 2009: 142-147.

Yan She-feng and Ma Yuan-liang. Sensor Array Beampattern Optimization: Theory with Applications [M]. Beijing: Science Press, 2009: 142-147.

[10]Candès E J, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J].IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[11]Candès E J, Romberg J, and Tao T. Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics, 2006, 59(8):1207-1223.

[12]Baraniuk R G, Candès E J, Elad M,et al.. Applications of sparse representation and compressive sensing[J].Proceedings of IEEE, 2010, 98(6): 906-909.

[13]Donoho D L. Compressed sensing[J].IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[14]Candès E J and Wakin M B. An introduction to compressive sampling[J].IEEE Signal Processing Magazine, 2008, 25(2):21-30.

[15]Romberg J. Imaging via compressive sampling[J].IEEE Signal Processing Magazine, 2008, 25(2): 14-20.

[16]Paredes J L, Arcw G R, and Wang Z M. Ultra-wideband compressed sensing: channel estimation[J].IEEE Journal of Selected Topics in Signal Processing, 2007, 1(3): 383-395.

[17]Potter L C, Ertin E, Parker J T,et al.. Sparsity and compressed sensing in radar imaging[J].Proceedings of IEEE,2010, 98(6): 1006-1020.

[18]贺亚鹏, 王克让, 张劲东, 等. 基于压缩感知的伪随机多相码连续波雷达[J]. 电子与信息学报, 2011, 33(2): 418-423.

He Ya-peng, Wang Ke-rang, Zhang Jin-dong,et al.. Compressive sensing based pseudo-random multi-phase CW radar[J].Journal of Electronics&Information Technology, 2011,33(2): 418-423.

[19]Tello A M, López-Dekker F, and Mallorquí J J. A novel strategy for radar imaging based on compressive sensing [J].IEEE Transactions on Geoscience and Remote Sensing, 2010,48(12): 4285-4295.

[20]Gurbuz A C, McClellan J H, and Scott W R. A compressive sensing data acquisition and imaging method for stepped frequency GPRs[J].IEEE Transactions on Signal Processing,2009, 57(7): 2640-2650.

[21]Suksmono A B, Bharata E, Lestari A A,et al.. Compressive stepped-frequency continuous-wave ground-penetrating radar[J].IEEE Geoscience and Remote Sensing Letters, 2010, 7(4):665-669.

[22]Shah S, Yu Y, and Petropulu A. Step-frequency radar with compressive sampling (SFR-CS)[C]. IEEE International Conference on Acoustics, Speech and Signal Processing,Dallas, TX, USA, March 14-19, 2010: 1686-1689.

[23]Malioutov D, Cetin M, and Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J].IEEE Transactions on Signal Processing, 2005,53(8): 3010-3022.

[24]贺亚鹏, 李洪涛, 王克让, 等. 基于压缩感知的高分辨 DOA估计[J]. 宇航学报, 2011, 32(6): 1344-1349.

He Ya-peng, Li Hong-tao, Wang Ke-rang,et al.. Compressive sensing based high resolution DOA estimation[J].Journal ofAstronautics, 2011, 32(6): 1344-1349.

[25]Gurbuz A C and McClellan J H. A compressive beamforming method[C]. IEEE International Conference on Acoustics,Speech and Signal Processing, Las Vegas, Nevada, USA,March 30-April 4, 2008: 2617-2620.

[26]Sadegh F and Abdel R S. An optimum adaptive single-port microwave beamformer based on array signal vector estimation[J].IEEE Transactions on Antennas and Propagation,2010, 58(3): 738-746.

[27]Davenport M. Random observations on random observations:sparse signal acquisition and processing[D]. Rice University,2010.

[28]Chen S S, Donoho D L, and Saunders M A. Atomic decomposition by basis pursuit[J].SIAM Review, 2001, 43(1):129-159.

[29]Candès E J and Tao T. The Dantzig selector: statistical estimation whenpis much larger thann[J].Annals of Statistics, 2007, 35(6): 2313-2351.

[30]Eftekhari A, Babaie-Zadeh M, Jutten C,et al.. Robust-SL0 for stable sparse representation in noisy settings[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, April 19-24, 2009: 3433-3436.

[31]Mohimani H, Babaie-Zadeh M, and Jutten C. A fast approach for overcomplete sparse decomposition based on smoothed L0 norm[J].IEEE Transactions on Signal Proessing, 2009, 57(1): 289-301.