一种码片内多径参数的最大似然估计算法
2012-07-25袁航剑洪一帆
袁航剑 洪一帆 罗 武 蒋 伟
(北京大学信息科学技术学院区域光纤通信网与新型光通信系统国家重点实验室 北京 100871)
1 引言
卫星移动通信信道是典型的多径信道。多径效应会导致接收信号产生衰落,也会引起码间串扰,严重地损害通信的质量。码分多址(Code Division Multiple Access, CDMA)是现在流行的通信技术,已经被许多系统采用[1,2]。码分多址技术具有很好的抵抗多径信道干扰的能力,它能够很容易地分辨出时延超过一个码片的多径并通过 Rake接收技术合并多径能量获得信噪比增益[3]。卫星信道典型多径时延扩展在100 ns量级[4],对于一些CDMA系统有可能在一个码片之内。例如CDMA2000 3X反向信道的扩频序列速率为 3.68 Mcps,即码片周期为 270 ns,移动卫星信道的多径时延很有可能小于码片周期。此时无法采用Rake接收技术,但在估计出多径参数的情况下仍然可以采用最佳接收技术获得更好的性能。卫星移动通信信道通常是两径信道[5],本文主要研究两径时延在一个码片内的多径参数估计问题。
现有的码片内多径参数估计算法大致如下:粒子滤波[6]多径分离性能好,但实现的复杂度较高。子空间分解算法[7]将接收信号分解为多个子空间,利用子空间之间的正交性来估计信道参数,优点是分辨率较高,但是实现的复杂度高。解卷积算法因具有噪声放大作用而失效,为此文献[8]对解卷积算法进行约束或者迭代处理以解决有脉冲成形情况下的参数估计问题。Pulse Subtraction算法[9]将多径信号相关函数近似成不同复振幅与时延的参考脉冲的叠加,通过对相关函数减去特定的参考脉冲来消除多径干扰。TK算法[10]通过 TK算符操作可以明显区分出相关峰的位置,TK算法同样适用于方波成形情况下的码片内多径参数估计问题。MEDLL算法[11]基于最大似然原理估计各径信号的时延、复振幅,但运算过程中涉及到复杂的矩阵迭代运算,为此文献[12]提出了简化MEDLL算法。算法首先通过消除第1径的影响来估计第2径的时延和复振幅,再通过消除第2径的影响来估计第1径的时延和复振幅,如此迭代进行。但是简化MEDLL算法迭代初始值存在一定的误差,该误差会导致算法不收敛,影响时延估计的性能。
本文提出基于最大似然的2维搜索算法,算法对两径时延进行2维搜索,同时对两径复振幅进行估计,通过使得目标似然函数最大化而找出最优的时延、复振幅估计值。提出基于最大似然原理的解相关复振幅估计算法结合时延2维搜索,该方案时延估计性能得到提高,但复振幅估计性能不理想。为此,又提出基于均方误差(Mean Squared Error,MSE)准则的近似线性最小均方误差(Linear Minimum Mean Squared Error, LMMSE)复振幅估计算法结合时延2维搜索,以提高复振幅估计性能。仿真证明采用近似的LMMSE多径复振幅估计算法结合两径时延2维搜索在时延、复振幅估计方面都具有良好的性能。
2 最大似然2维搜索算法
本文主要考虑两径信道、且两径时延差在一个码片附近情况下的参数估计问题。在 CDMA通信中,多径的存在通常不会导致载波频偏消除和伪随机(Pseudo-Noise, PN)码捕获无法进行,而只是对同步的精度造成影响。在初始同步之后,如果进一步估计出多径的参数可以提高解调性能。为简单起见,此时需要估计的多径参数包括两径的精确时延和复振幅,而不包括接收信号的频偏。从最大似然估计的角度出发,需要对两径时延和复振幅联合起来进行多维搜索再择优判决,但这将导致搜索的次数过多,尤其是对复振幅的搜索更是严重地增加了算法的复杂度。因此本文考虑只对两径的时延在小范围内进行2维搜索。在每一对两径时延的搜索值上,对两径复振幅进行估计,得到一些两径时延和复振幅的备选组合。最后通过计算这些备选组合的似然函数,挑选使似然函数最大化的一组两径时延和复振幅值作为估计值。对两径参数的估计,本文主要考虑利用码分多址通信中的导频信号来进行。
接收到的导频信号可以表示如下:

式中h(t)发送滤波器的单位冲激响应,n是chip编号,τ1和τ2是第1、第2径信号时延,φ1和φ2是第1、第2径信号相位,α1(t)和α2(t)是两径衰落系数。cn是扩频的伪随机序列即PN 码,Tc是chip持续时间。n(t)为加性复高斯白噪声,噪声功率谱密度为N0。
接收信号经过匹配滤波及与本地PN码相关之后得到相关函数为


接收信号的对数似然函数为

最大似然2维搜索算法目标即是找到使得式(3)最大的A1,τ1,A2,τ2。考虑到PN码的初始同步已经完成,即接收机已经搜索到相关峰所在位置,由于存在第2径的影响,所以相关峰所在位置与第1径的位置有误差。但考虑到第1径信号的平均功率大于第2径,全局最大值与第1径的位置的误差不会很大。所以在相关峰所在位置附近的一个小范围内搜索第1径。对于每一个可能的第1径时延,在其后的一定范围内搜索第2径。对每一组可能的第1、第2径时延值组合,估计出第1、第2径的复振幅,然后代入式(3)求出对数似然值。似然值最大所对应的一组时延、复振幅值即为最大似然估计值。
对于一组可能的第 1、第 2径时延值组合,可以从最大似然原理出发求解第 1、第 2径复振幅。基于最大似然原理可以推导出解相关运算估计两径复振幅。
2.1 解相关求第1、第2径复振幅
考虑最大化式(3),可以将式(3)对A1,A2求导得到

满足式(4)的A1,A2的解即为两径复振幅最大似然估计值。对式(4)进行求解可得
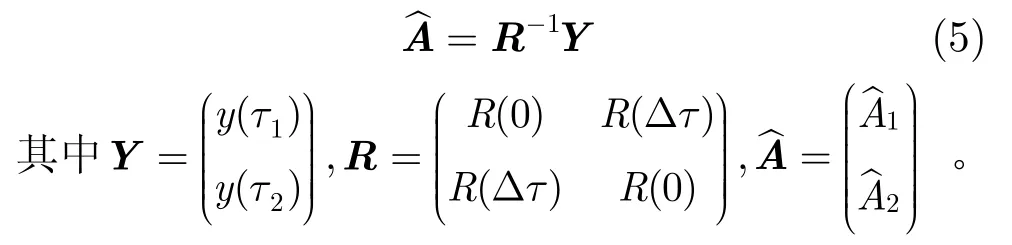
式(5)即为解相关求解两径复振幅的公式。由式(5)可以看出,根据接收信号相关函数,以及第1、第2径时延值,即可求出第1、第2径的复振幅。
解相关运算求解两径复振幅是基于最大似然原理,目标是使得接收相关矩阵Y的估计误差最小。但是在两径时延搜索间隔较小时,解相关矩阵R趋于奇异,导致复振幅估计值急剧增加而使复振幅偏离真实值,致使复振幅估计性能不理想。因此,可以考虑采用LMMSE准则来对A1,A2进行估计。
2.2 LMMSE算法估计第1、第2径复振幅
分别将τ1,τ2代入式(2)可得
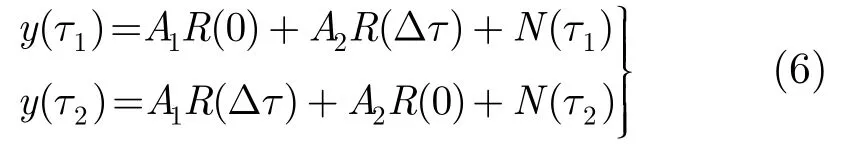
写成矩阵形式

由式(7)可得A的LMMSE[13]估计值:

CAA,CN分别是信号和噪声的协方差矩阵。P1,P2分别为第1、第2径信号功率。这里考虑两径复振幅相互独立。当对接收相关函数的采样值在一个码片之内时,N1,N2具有一定的相关性,这儿为了讨论方便,假设N1,N2相互独立。
由式(8)看出,它与式(5)只相差RΔ项,RΔ中只有N0/MTmP1,P1/P2为未知量。N0/MTm P1与接收信号解扩后的信噪比有关,经过初始同步后,接收端可以得到接收信号信噪比的粗估计值或者可能的范围。实际应用的时候,根据估计得到的信噪比范围,可对N0/MTm P1设置一个典型值。P1/P2为第1、第 2径信号功率之比,对于实际情况可以考虑P1/P2的取值范围在3~8 dB。当P1/P2较大时,第2径对解调性能的影响可以忽略,这时也就无需对第2径时延、复振幅进行估计。实际应用时,可以对P1/P2设置典型值,由此带来的性能影响,下文仿真中可以看到。
通过对噪声独立性的近似,以及对信噪比及两径信号功率比取典型值,即可得到近似LMMSE复振幅估计算法。
2.3 最大似然2维搜索算法流程
上文讲述了基于最大似然时延 2维搜索的思想,并且提出了两种复振幅估计方法,具体的参数估计算法包含以下4个步骤:
(3)将第(2)步的时延值组合及相应的复振幅计算值代入式(3)计算出对应的似然值。
(4)似然值最大所对应的第1、第2径时延、复振幅值组合即为两径时延、复振幅估计值。
3 仿真结果
在不同信噪比、两径时延差在0.25Tc~1.50Tc范围内随机分布情况下,对上述算法进行仿真。仿真条件为升余弦脉冲成形,滚降系数0.22, 64倍过采样,扩频比 255,累加样本数M= 1 00。在最大似然2维搜索算法第(2)步中,仿真参数的取值如下:ΔT= 0 .25Tc,TS=Tc/64,P取 32,n取 16,q取96。
仿真信噪比Ec/N0的范围为 - 2 2 ~-16 dB(Ec为chip能量),接收信号经过解扩和多样本累加之后的等效信噪比范围为22 ~ 2 8 dB , LMMSE算法中设置典型值N0/MTmP1= 2 5 dB ,对应Ec/N0=-1 9 dB 。对于不同的第1、第2径信号功率,LMMSE算法中设置典型值为P1/P2= 5 dB。
图1,图2为第1、第2径功率径差3 dB情况下解相关最大似然2维搜索、LMMSE最大似然2维搜索和简化MEDLL算法3种算法时延、复振幅估计性能仿真结果。‘LMMSE-典型’表示LMMSE算法中两径信号功率差取典型值P1/P2= 5 dB,‘LMMSE-真实’表示LMMSE算法中两径信号功率取真实值P1/P2= 3 dB 。‘-1’表示第1径估计性能,‘-2’表示第 2径估计性能。几种算法各自的第 1径和第2径复振幅估计性能相近,所以图中各种算法复振幅估计性能都只画了一条线。
可以看出两径信号功率比分别取典型值和实际值时,LMMSE最大似然2维搜索算法的时延、复振幅估计性能几乎一致,且幅度性能都优于解相关最大似然2维搜索和简化MEDLL算法。解相关最大似然2维搜索和LMMSE最大似然2维搜索算法的第1、第2径时延估计性能相近,且第2径的时延估计性能明显优于简化MEDLL算法。主要是因为简化MEDLL算法迭代初始值存在一定的误差,该误差会导致算法不收敛,影响时延估计的性能。解相关最大似然2维搜索算法的复振幅估计性能不理想,主要是因为在两径时延2维搜索时,当两径时延较小时,解相关矩阵R趋于奇异,导致复振幅估计误差变大,最终影响估计性能。
图3、图4为第1、第2径功率径差8 dB情况下的仿真结果。‘LMMSE-典型’表示两径信号功率取典型值P1/P2= 5 dB ,‘LMMSE-真实’表示两径信号功率取真实值P1/P2= 8 dB 。
同样,两径信号功率比取典型值和实际值时,LMMSE最大似然2维搜索算法的时延、复振幅估计性能几乎一致。解相关最大似然 2维搜索和LMMSE最大似然2维搜索算法的第1、第2径时延估计性能相近,且第2径的时延估计性能明显优于简化MEDLL算法。LMMSE最大似然2维搜索算法的幅度估计性能与简化MEDLL算法相近,但都优于解相关最大似然2维搜索算法。
由以上仿真结果可以看出,解相关最大似然 2维搜索算法时延估计性能虽然得到改善,但是复振幅估计性能不理想。近似LMMSE算法中第1、第2径功率比取典型值较真实值所带来的估计性能损失不明显,并且近似LMMSE算法克服了解相关算法复振幅估计性能不理想的缺点。

图1 两径信号功率差3 dB,时延估计性能比较

图2 两径信号功率差3 dB, 复振幅估计性能比较
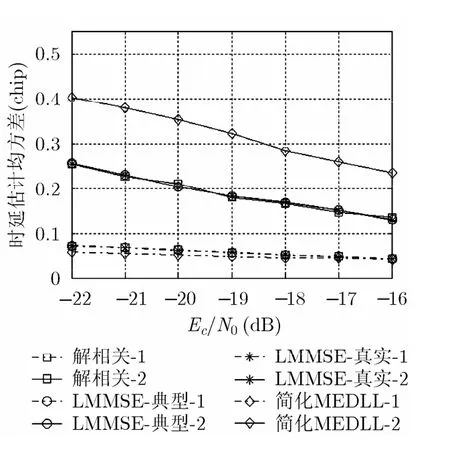
图3 两径功率差8 dB, 时延估计性能比较

图4 两径功率差8 dB,复振幅估计性能比较
4 结束语
本文针对码分多址卫星移动通信中道码片内两径参数估计问题,提出了基于最大似然的2维搜索算法。算法对两径时延进行2维搜索,同时对两径复振幅进行估计。首先提出两径时延2维搜索结合解相关复振幅估计算法的方案,该方案时延估计性能得到提高,但复振幅估计性能不理想。然后又提出两径时延2维搜索结合采用近似LMMSE算法进行多径复振幅估计的方案,仿真结果表明其时延、复振幅估计性能都比较理想。
[1]3GPP TS 25.211 v11.0.0. Physical channels and mapping of transport channels onto physical channels (FDD)[S].2011-2012.
[2]3GPP2 C.S0002-D v2.0. Physical layer standard for CDMA2000 spread spectrum systems[S]. 2005.
[3]Doukeli A P, Lioumpas A S, Karagiannidis G K,et al..Increasing the efficiency of RAKE receivers for ultrawideband applications[J].Wireless Personal Communication,2012, 62(3): 715-728.
[4]Lu Song-tao, Liu Tai, and Zheng Meng. A wideband space time statistical model for characterization of satellite communication channel in dense multipath environment[C].Proceedings of 71th Vehicular Technology Conference, Taipei,China, May 16-19, 2010: 1-5.
[5]Ibnkahla M, Rahman Q, Sulyman A,et al.. High-speed satellite mobile communications: technologies and challenges[J].Proceedings of the IEEE, 2004, 92(2): 312-339.
[6]Closas P, Fernandez-Prades C, and Fernandez-Rubio J A. A Bayesian approach to multipath mitigation in GNSS receivers[J].IEEE Journal of Selected Topics in Signal Processing, 2009, 3(4): 695-706.
[7]付龙飞, 张水莲, 辛刚. 高精度多径延时估计[J]. 电子技术应用, 2011, 37(8): 120-123.
Fu Long-fei, Zhang Shui-lian, and Xin Gang. Super-resolution estimation of multipath time-delays[J].Application of Electronic Technique, 2011, 37(8): 120-123.
[8]Lohan E S, Hamila R, Lakhzouri A,et al.. Highly efficient techniques for mitigating the effects of multipath propagation in DS-CDMA delay estimation[J].IEEE Transactions on Wireless Communication, 2005, 4(1): 149-162.
[9]Lohan E S and Renfors M. Feedforward approach for estimating the multipath delays in CDMA systems[C].Proceeding of Nordic Signal Processing Symposium,Kolmarden, Sweden, June 2000: 125-128.
[10]Shamsi K R, Yang Dong-kai, Siddiqui A A,et al..Experimental evaluation of Teager-Kaiser discriminator under multipath environment for GPS signal[C]. Proceedings of IEEE 6th Conference on Industrial Electronics and Applications, Beijing, China, June 21-23, 2011: 991-995.
[11]Van Nee R D J and Siereveld J. The multipath estimating delay locked loop: approaching theoretical accuracy limits[C].Proceeding of IEEE Position Location and Navigation Symposium, Las Vegas, NV, USA, Apr. 11-15, 1994:246-251.
[12]Van Nee R D J. Method of estimating a line of sight signal propagation time using a reduced multipath correlation function[P]. U.S. Patent, 5615232, 1997.
[13]Kay S M and Luo Peng-fei. Fundamentals of Statistical Signal Processing, Estimation Theory[M]. Fourth Edition,Englewood Cliffs, NJ: Prentice Hall, 1993: 315-316.
