支持媒体处理的子字绝对值单元设计与实现*

开耀文，高德远，张 萌

(西北工业大学计算机学院，西安710129)

1 前言

当前，为了满足多媒体应用的需要，很多通用处理器提供了针对多媒体应用的扩展指令。如Intel的MMX，AMD 的3DNow!，以及 Motorola的 AltiVec等。

多媒体应用具有两个基本特点:数据并行度高和数据精度要求低［1］。子字并行技术是一种单指令流多数据流技术，它的原理是一条指令中的数据可以拆分成多个子字并行执行。例如AltiVec指令集中，参与计算的操作数位数为128位，这些操作数可以选择4个32位字的，或者8个16位半字，或者16个8位字节进行运算。子字并行运算的特点正好与多媒体应用的特点相符合，是一种有效提高多媒体应用性能的手段。

在图像处理中，两个数的绝对值运算|A-B|得到了广泛应用，例如视频中的运动估计和预测算法中就采用了大量的这种绝对值运算。在没有实现绝对值单元的通用处理器中，实现一个无符号绝对值运算需要进行A-B和B-A运算，并将结果相或，实现一个有符号绝对值运算则需要更复杂的步骤。而采用了绝对值单元的处理器只需要一条指令就能实现通用处理器中需要多条指令实现的绝对值运算。绝对值单元在减少计算指令数的同时减少了访存次数，因为绝对值运算只需要一次取出操作数做运算，而不用像通用处理器那样需要多次取数。绝对值运算是建立在普通减法运算基础上的，通过扩展原有加法器实现绝对值单元可以使普通的加法器与绝对值单元共享一个计算单元，这样实现绝对值单元的代价是较小的。

2 并行前缀加法器原理

2.1 加法器原理

考虑加法器的进位传播公式［2］:

单个进位生成和not kill信号给出如下:

公式(1)和(2)的信号可以概括地描述为:在多位组所包括的位z...x范围内，可分成高位组和低位组两个子组，进位生成信号是由两方面决定的:高位子组z….y生成进位信号或者低位子组y-1...x生成进位，而低位子组的生成进位信号不被“杀死”。如果高位子组和低位子组的都不“杀死”进位，那么这个组也不“杀死”进位。

公式3说明第i位的进位信号即是第i-1位到第0位的组进位生成信号。根据求和公式Si=Pi8 ci可得到A与B的和，其中Pi为单个位的进位传播信号，Pi=Ai8Bi;Si为和的第i位。

因此，加法可以缩减为三步来进行［3］:

(1)使用公式4和5按位计算进位生成和not kill信号;

(3)结合公式3和求和公式计算求和信号。

显然，进位生成逻辑是整个计算的关键。加法器运算的优化核心就是减小进位信号的生成时间。由此引出了各种优秀的加法器设计，如超前进位加法器，条件加法器，旁路进位加法器和并行前缀加法器。其中，相对于其它加法器结构，并行前缀加法器对于位宽较大的加法运算(N＞16)可以较好的控制延时增长，通过构造多级结构可以取得以logN增长的延时［3］。通过构造并行前缀树，快速的计算出各个位的进位信号，从而快速计算出加法结果。

2.2 并行前缀树原理

1.并行前缀计算公式如下［4］:

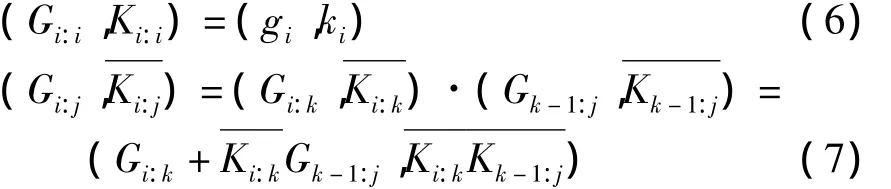
式中，“·”算符为前缀计算算符。前缀计算算符具有两个重要的计算性质:结合律及幂等律，即满足以下公式:

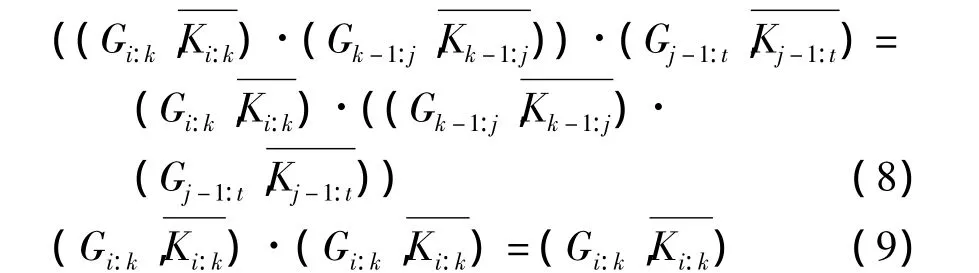
结合律使得整个计算式可以并行计算，幂等律允许各并行计算子项交叠执行，从而给并行前缀加法器的构造带来很大的灵活性［5］。不同的并行前缀加法器正是对并行子项的不同区间运用了结合律和幂等率而得到的。图1给出了ladner-Fischer［6］的并行前缀树示意图，图中黑点采用公式1和2，灰点采用公式1。ladner-Fischer树的构造较为简单，各个计算子项没有重叠，计算层数达到最优。

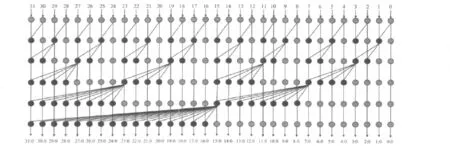
图1 32位ladner-Fischer加法器并行前缀树示意图

3 绝对值运算的研究与设计

通常，计算绝对值的方法是将两个数大小进行比较，再根据比较的结果，用大值减去小值，或者直接计算两个数的减法，再对结果取正值。硬件实现中［7］，这种计算方法需要两步运算。显然，两步运算增加了关键路径的长度，从而对整个运算的时序产生影响。为了消除这样的两步运算，可以通过另外一种方法解决［8］。这种方法的思想基于条件加法器，即同时计算A-B和B-A，通过计算结果的符号位选择结果为正数的计算通路。

然而，这种方法在减小关键路径的同时，大大增加了计算单元的面积，因为它引入了两条计算通路。

3.1 绝对值运算的分析

通过观察发现，无论用何种方法，绝对值运算中，两个数的减法运算是必须的过程。同其它运算一样，绝对值运算的操作数也分有符号数和无符号数，以下分别通过有符号操作数和无符号操作数来分析绝对值运算。

3.1.1 有符号绝对值运算

对于有符号数，补码的加减法运算是最常见的运算方法，因为有符号数补码减法可以转化为有符号数补码加法的运算，所以这里讨论的都是基于补码的运算法则，并且参与运算的两个数都为有符号数。约定A为A的所有位取反。A-B=A+(B+1)，B=-(B+1)，在加法运算前将B的所有位取反得到的结果为A-B-1。如果这个值是正数，加法器的结果加1就是绝对值的计算结果。反之，如果加法器的结果是负数，将加法器结果的所有位取反得到的结果为-(A-B-1+1)=B-A，也为绝对值的结果。所以，绝对值运算可以实现为在加法器中加入两个控制信号:和加一信号inc和取反信号inv，并且其中一个操作数在送入加法器中时全部取反。显然，inc=inv。如果加法器结果的符号位为负，则将加法器结果的全部位取反即可。如果加法器结果的符号位为正，则还要对加法器的结果加1。

3.1.2 无符号绝对值运算

两个有n个数字的二进制无符号绝对值|M-N|可按以下步骤进行:

(1)将被减数M与减数N的补码相加，即:

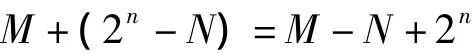
(2)当M＞=N，M-N的值即为绝对值的大小。观察发现，如果M＞=N时，结果将产生进位2n，舍去这个进位，得到的就是M-N。

(3)当M＜N，那么N-M的值即为绝对值的大小，对于这种情况，将被减数M与减数N的反码相加，即:

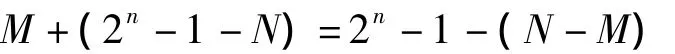
由于N＞M，结果和不会产生进位，且为N-M的反码，将结果取反即可得到N-M的值。通过以上分析可知，无符号绝对值运算与有符号绝对值运算具有共同的性质，总结如下:

·两操作数之一需要求反送入加法树中，即进行减法运算;

·对加法树出来的结果位处理方式相同，取反或者结果加1。

显然，取反运算相对于结果加1运算的延时小很多。所以，结果加1处于关键路径上。最坏情况下，加1运算的进位传播延时经过加法器结果的每一位，这对于整个计算单元时序的影响是很大的。定义需要对加法器结果的和进行加1的运算为和加一运算。为了消除对加法器结果的加一运算，需要研究和加一运算的性质。

3.2 和加一运算

考虑和加一运算的重要性，定义和加一运算的进位信号为CA，则第i位的进位信号为CAi。CAi信号与原本的c(i)信号是有联系的:如果c(i)=1，显然 CAi=1;如果 c(i)=0，而且 i-1…..0组不“杀死“进位，即=1，则 CAi=1，所以 CAi=。由以上描述可得:

将式3代入得到:

其中，inc为和加一运算控制信号。所以和加一运算的求和公式为SAi=CAi8Pi，其中SAi为A与B和加一运算结果的第i位。

输出逻辑如图3所示。

4 子字并行绝对值单元的设计

通过分析加法器的结构可知，要想实现子字并行运算，最重要的是要控制低位子字的进位对高位子字产生影响。例如，在AltiVec指令集中，基于字节运算的指令要消除在7+8*i(0≤i≤15)位上产生的进位。所以，需要一个控制逻辑来控制低位进位需不需要传播到高位，对于32位字，对最短子字长度为8的加法器单元，通过给出的控制信号，可以同时计算4个字节，或2个半字，或一个字的加法。如表1所示。

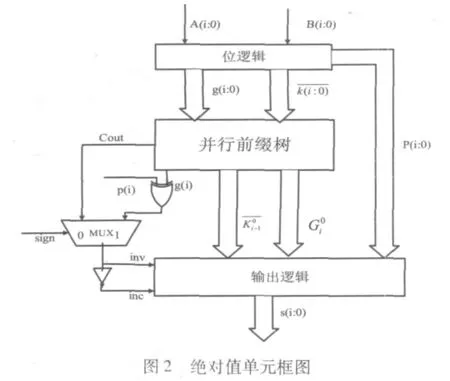
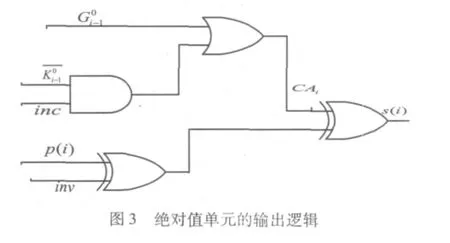
表1 控制信号

在一般的子字并行加法器设计中，控制逻辑只要控制了进位的传播就能实现子字并行加法。当需要进行子字加法时，屏蔽相邻位的进位;反之，允许进位。基于此原理，提出了进位控制机制:进位截断机制［1］。该方法的思想是，在并行前缀加法器的并行前缀树结构中，当需要进行子字并行运算时，控制低位的进位对高位的影响，即在子字的边界处设置控制信号，消除进位的传播。

参照这种思想，对于子字并行绝对值的运算也可以通过设置控制位截断进位的方式来实现。通过比较分析，子字并行绝对值单元在绝对值单元上做如下改进:

(1)采用与子字并行加法器相似的进位截断机制，根据控制信号的有无决定是否将低位的进位信号传递到高位。

(2)根据绝对值运算的特点，需要获得最小子字(8位)进位和符号位。以决定对结果进行取反还是加一操作。

通过以上分析可知，子字并行绝对值单元的结构框图如图4所示。

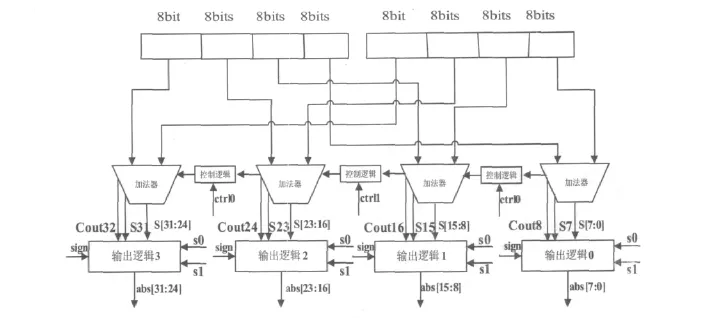
图4 32位子字并行绝对值单元

输出逻辑如图3，由于要实现子字并行，所以相应的inc和inv如下:

输出逻辑0:inv0_7=(inv8＆～S0＆～S1)|(inv16＆S0＆ ～S1)|(inv32＆S0＆S1);

输出逻辑1:inv8_15=(inv16＆～S0＆～S1)|(inv16＆S0＆ ～S1);

输出逻辑2:inv16_23=(inv24＆～S0＆～S1)|(inv32＆S0＆ ～S1)|(inv32＆S0＆S1);

输出逻辑3:inv24_31=(inv32＆～S0＆～S1)|(inv32＆S0＆S1)

其中 invx=sign?sx-1:coutx(x 为8，16，32)

5 实现与性能分析

5.1 实现

采用verilog语言实现了以上讨论的32位子字并行绝对值单元的可综合设计，同时实现了前面所讨论的其它可实现绝对值单元的方法，并使之并行化。文献［7］中没有经过优化的绝对值单元为方案1，文献［8］中采用条件加法器思想的绝对值单元为方案2，经过优化的绝对值单元为方案3。使用Modelsim对3种方案的设计进行仿真，仿真数据的输入采用随机数，运算模块的输出结果同相对应的行为级的输出结果比较，结果全部正确。为了比较3种方法的面积与延时，采用synopsys Design Complier［9］工具进行逻辑综合，为了体现公平性，所有绝对值单元中的加法器结构都是用ladner-Fischer前缀加法器，不采用 synopsys DesignWare［10］中的基本加法单元。在TSMC 0.13um工艺下对这三种方案的子字并行绝对值进行了实现并测试了它们的性能，时序/面积报告如表2所示:

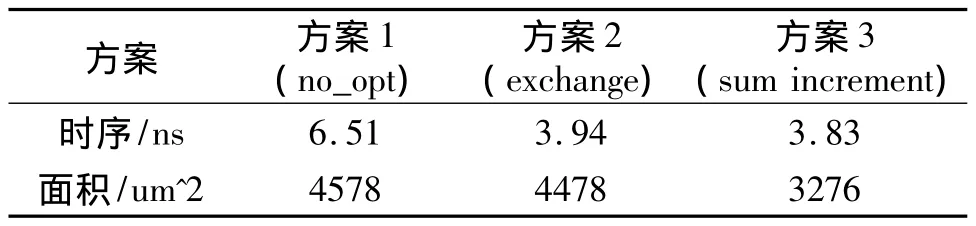
表2 子字并行绝对值单元时序/面积报告

三种方案的绝对值单元的时序/面积报告如表3所示。

表3 绝对值单元时序/面积报告

5.2 性能分析

通过时序/面积报告可以看出，没有实现子字并行的绝对值单元中，方案1的面积与方案3的面积相当，但方案3的时序明显好于方案1。方案2的时序与方案3相当，但方案3的面积比方案2小很多。从前面分析可知，方案2采用了两个加法器同时计算A-B和B-A，所以面积大了很多，而方案1是采用时间换取面积的方式，通过加法器计算结果来进行下一步运算，所以它的延时较大。方案3综合了前两种方案的优点，所以它的延时与面积都与前两种方案的最好形式相当。通过对和加一运算的分析，使得在加法器的运算过程中可以同时进行A+B和A+B+1运算，所以采用方案3方法实现的绝对值单元在减小面积的同时，也减小了整个运算单元的延迟。

子字并行绝对值单元是在绝对值单元的基础上增加了一些控制低位进位的逻辑，所以延时和面积较绝对值单元要大一些，但增加的不是很明显。相比较其它方案，方案1中，子字并行绝对值单元的面积比绝对值单元大了很多。这是因为方案1中的绝对值单元是在加法器结果出来后，通过判断加法器的进位或符号位来决定对结果取反还是加一。因为每一个加法器模块后面都有一个实现加一运算的加法器，为了实现子字运算，每个相应的8位，16位和32位子字都需要这样的加一运算，所以导致方案1的面积大大增加。

6 结束语

子字并行运算作为加速多媒体运算的有效方式，在各种媒体处理(比如音频和视频)需要的大量运算中得到了充分利用。该文分析了基于前缀加法器的子字并行绝对值单元的实现方法，并重点介绍了优化绝对值单元中的和加一运算，结合前缀加法器的特性，使得加法器可以同时进行A+B和A+B+1运算。分别实现了各种绝对值单元和子字并行单元并进行了比较。结果显示:优化的子字并行绝对值单元在面积上克服了条件绝对值单元的不足，同时又保持了条件绝对值单元牺牲面积所带来的时序优势，在整体性能上优于前文提出的绝对值单元。

［1］ 马胜，黄立波，王志英，等.子字并行加法器的研究与实现［J］.计算机工程与应用，2009，45(36):54-58.

［2］ N Burgess.The flagged prefix adder and its application in integer arithmetic［J］.VLSI Signal Process，2002，31(3):263-271.

［3］ Neil H.E.Weste，David Harris.CMOS超大规模集成电路设计［M］.汪东，等译.北京:中国电力出版社，2006.

［4］ Weinberger A，Smith J L A.A logic for high-speed addition［J］.National Bureau of Standards Circular，1958，591:3-12.

［5］ Beaumont-Smith A，Um C C.Parallel prefix adder design［C］.Pro-ceedings of 15th IEEE Symposium on Computer Arithmetic，2001:218-225.

［6］ Ladner R E，Fischer M J.Parallel prefix computation［J］.ACM，1980，27(4):831-838.

［7］ Carlson，D.A，Castelino，R.W，Mueller，R.O.Multimedia extensions for a 550-MHz RISC microprocessor［J］.IEEE Journal of Solid-State Circuits，1997，32(11):1618-1624.

［8］ S.C.Knowles.Arithmetic processor design for the T9000 Transputer［C］.Proc.SPIE，1991:230-243.

［9］ Synopsys Inc.Design compiler user guide［M］.Mountain View:Synopsys，2007.

［10］ Synopsys Inc.DesignWare building block IP user guide［M］.Mountain View:Synopsys，2007.