基于区间敏度分析的拓扑优化设计
2012-07-25李家春
李家春 张 萍
贵州大学,贵阳,550003
0 引言
工程结构的设计常常受制于材料属性、几何参数、作用载荷及其他参量的不确定性,处理不确定性问题的传统方法是通过安全因子来进行的。近年来,基于区间分析方法的工程结构优化设计逐渐得到重视并付诸于工程实践[1-2]。
区间分析方法是在区间数学的基础上发展起来的一种新的解决工程结构不确定性问题的分析方法,它基于较少的数据(不确定参数的上下界)解决一系列不确定性问题,能得到令人满意的结果。该方法作为随机不确定模型的有益补充,具有较好的发展前景[3-5]。
在实际工程结构设计中,需要合理地定量处理影响工程结构性能的各种不确定性问题,将区间分析方法引入连续体拓扑优化设计领域是解决此类问题的方法之一。邱志平等[6]以区间数学理论为基础,提出了用区间方法进行非线性结构灵敏度分析的方法。本文将这种区间敏度分析思想引入到连续体结构拓扑优化设计之中,建立能有效求解结构最优拓扑的子区间基移动算法。
1 基于双向插值方法的区间摄动有限单元分析方法
尽管区间优化问题的求解比确定性优化问题的求解复杂,但区间分析方法比确定性分析方法得到的信息更多[7-8]。在连续体拓扑优化中,敏度分析可采用区间分析方法进行求解。基于密度方法的连续体拓扑优化敏度表示的是一种有限单元间的密度变化对目标函数产生的不同影响。由于这种影响是一种相对影响,故采用区间分析方法来求解目标函数或约束函数的相对敏度。这种相对敏度表征了在更广的设计域上的目标/约束函数的响应。而基于区间的相对敏度是实数,故可利用成熟的规划方法求解优化问题。
1.1 基于双向插值函数的区间优化模型
在双向插值函数模型中,假设材料的弹性张量是各向同性的。泊松比为常量,且与密度无关,而弹性模量随相对密度ρ的变化而变化,为直观起见,用变量xi代替i单元的相对密度ρ。
双向插值模式的刚度矩阵Ki、柔度函数C可表示为
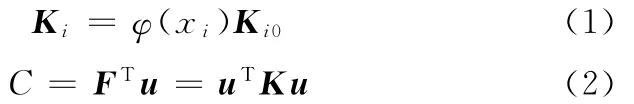
式中,φ(xi)为双向插值函数;Ki0为第i单元的初始刚度矩阵;u为结构位移;F为载荷。
φ(xi)的表达式为
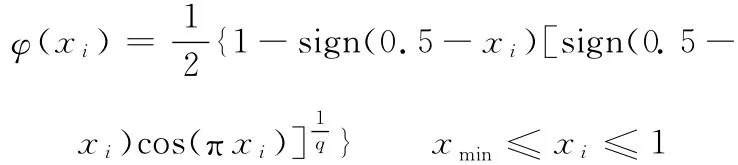
式中,q为惩罚参数。
总刚度矩阵K为
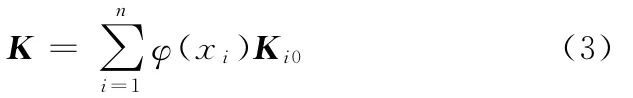
弹性模量Ei为

式中,Ei0为上一迭代步的第i单元弹性模量。
双向插值模型中结构单元弹性模量的控制参数是xi和惩罚参数q。q取不同值时,中间密度单元xi的弹性模量参数有逼近0或1的趋势。
设计变量x= (x1,x2,…,xn)T(0≤xi≤1),写为区间向量形式:

在实际优化分析中,不希望每次敏度分析的所用区间都是设计变量的原始区间,为此可以构建既能体现局部信息,又能表征优化问题全局性的子区间可变带宽基移动优化策略。其基本思想是:在初始计算分析时,在设计变量区间内选一初始子区间:
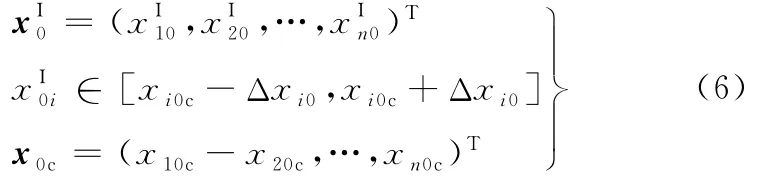
根据区间分析方法进行敏度分析计算,用相应的标准优化方法求设计区间中心(基)的移动xk+1,c=xk,c+dk,k为迭代次数,dk为步长。
1.2 基于双向插值模式的敏度分析摄动近似计算方法
以拓扑优化问题中典型的柔度函数为目标函数,以体积约束为约束条件,分析基于区间的相对拓扑敏度。
体积函数表达式为

式中,Vi为结构第i单元的体积;V*为初始结构体积;f为体积分数。
弹性静力结构控制方程为

由双向插值方法可知,刚度矩阵K=K(x),x∈xI,是设计变量的直接函数,而u为设计变量的间接函数,故位移响应可表示为
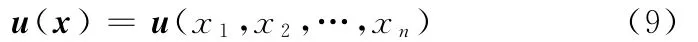
如果在优化过程中载荷F保持不变,则柔度函数对设计变量xi的相对区间敏度可通过对设计变量xi的合适区间扩展得到,敏度求解可表示为
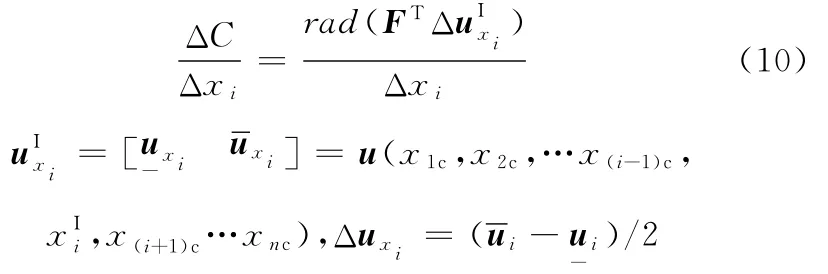
式中,rad(·)为求取区间半径的函数。
上述设计变量中,只有是区间参数,其他设计变量x1c,x2c,…,x(i-1)c,x(i+1)c,…,xnc皆为实参数。
要求解柔度函数的敏度信息,关键是如何正确高效地求解Δ。令设计向量x在第i设计变量上的区间扩展为x(i+1)c,…xnc),则K(x)u=F的矩阵区间扩展为区间参数方程为

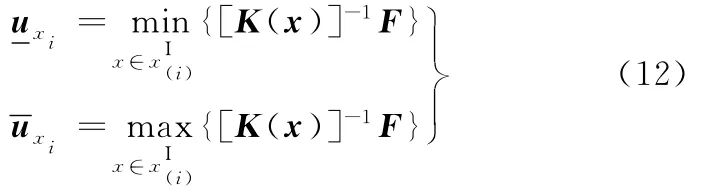
根据结构力学单元刚度组装的原则,将每个单元刚度矩阵扩展为维数与总刚度矩阵相同的子矩阵,其实现方法是将单元刚度矩阵的值对应赋予扩展单元刚度矩阵相对位置,其余元素为0。如此便得
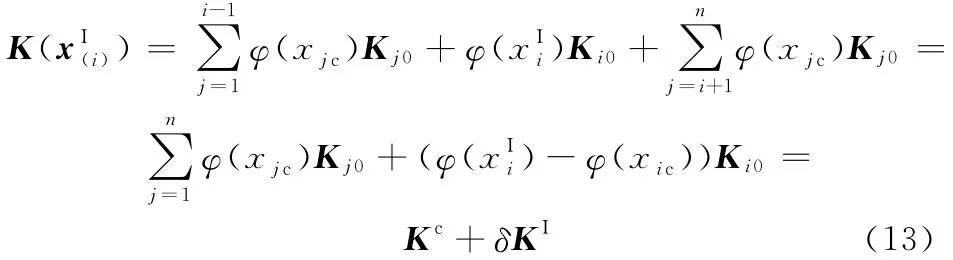
式中,Kc为标称刚度矩阵,δKI为摄动区间刚度矩阵。
由结构有限元静力摄动理论,标称结构有限元控制方程为

相应的摄动控制方程为
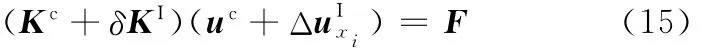
分解式(15),得
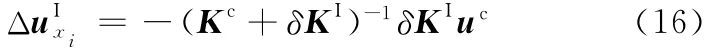
由式(16)有
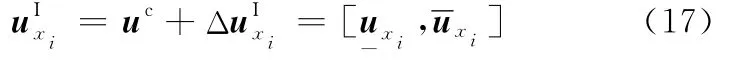
将式(16)代入式(10)中的柔度函数相对敏度计算公式得
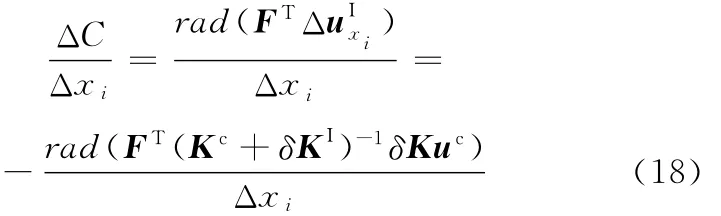
从式(18)可以看出由于Kc、uc、FT只与标称结构有关,而δKI、Δxi只与结构第i单元区间参数有关,简化高阶项,可将式(18)简化为
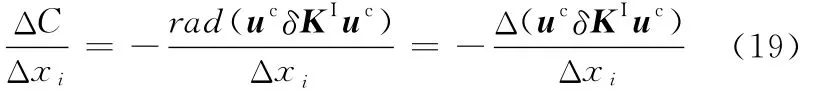
2 基于区间敏度分析方法的拓扑优化算法
在构建连续体拓扑优化算法的过程中,采用了固定带宽的敏度分析子区间,优化的参数为区间的中心值。换言之,就是在优化过程中,用一定带宽的盒子对整个设计域进行搜索,以确定最优设计变量所在的区间,盒子的搜索方向即基移动方向由盒子上的区间敏度决定。合适的固定带宽可使优化问题得到收敛全局解,优化过程中带宽可变,并采用一定策略控制带宽按一定尺度逐渐减小,构建变带宽基移动优化方法。
2.1 优化模型
以结构总体柔度为拓扑优化的目标函数,将结构的体积作为优化的约束条件,在给定载荷和边界条件基础上,基于双向插值的区间优化模型为
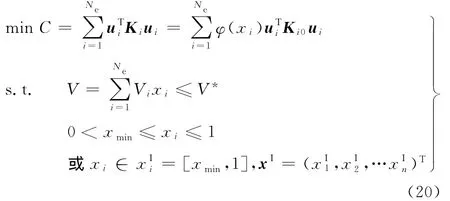
式(20)中,为避免总刚度矩阵奇异,取单元最小相对密度xmin=0.0015。
取优化初始点为
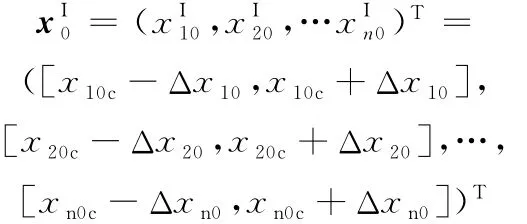
初始设计变量带宽取Δx10=Δx20=…Δxn0=0.1。第k次迭代计算时目标函数的敏度可根据式(19)计算。
2.2 优化算法
基于双向插值的区间敏度分析连续体拓扑优化准则设计变量的迭代策略如下:
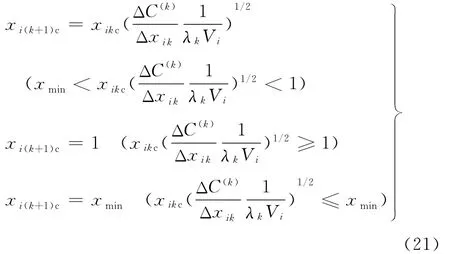
其中,xi(k+1)c为第k+1次迭代第i区间变量中心值,λk为第k次迭代时体积约束的拉格朗日乘子,拉格朗日乘子λk按罚乘子法思想进行迭代计算:
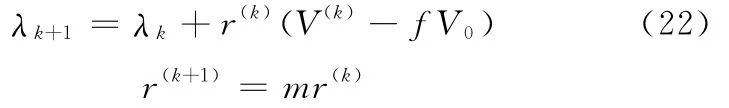
式中,V(k)为第k次迭代设计域体积;m为增长系数,取m=2~4。计算时取初始值:λ0=1,r(0)=0.25。
3 基于区间敏度分析方法的拓扑优化算法数值实现
3.1 悬臂梁优化数值实现
在拓扑优化邻域,悬臂梁设计问题被广泛用作优化问题研究时的测试、检验问题。以柔度最小化为目标函数,保留25%的体积。材料弹性模量E=200GPa,泊松比υ=0.3。梁的左端固支约束,右端受垂直向下作用力F,模型可近似为二维平面应力问题。结构离散为60×30四节点四边形单元。图1为结构模型示意图。图2所示为优化结果,结构优化边界从模糊到清晰。图3所示为目标函数值收敛情况。
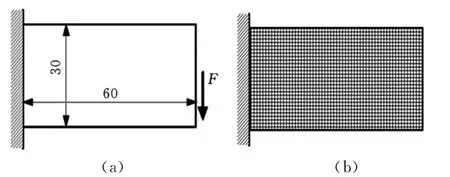
图1 悬臂梁有限元模型
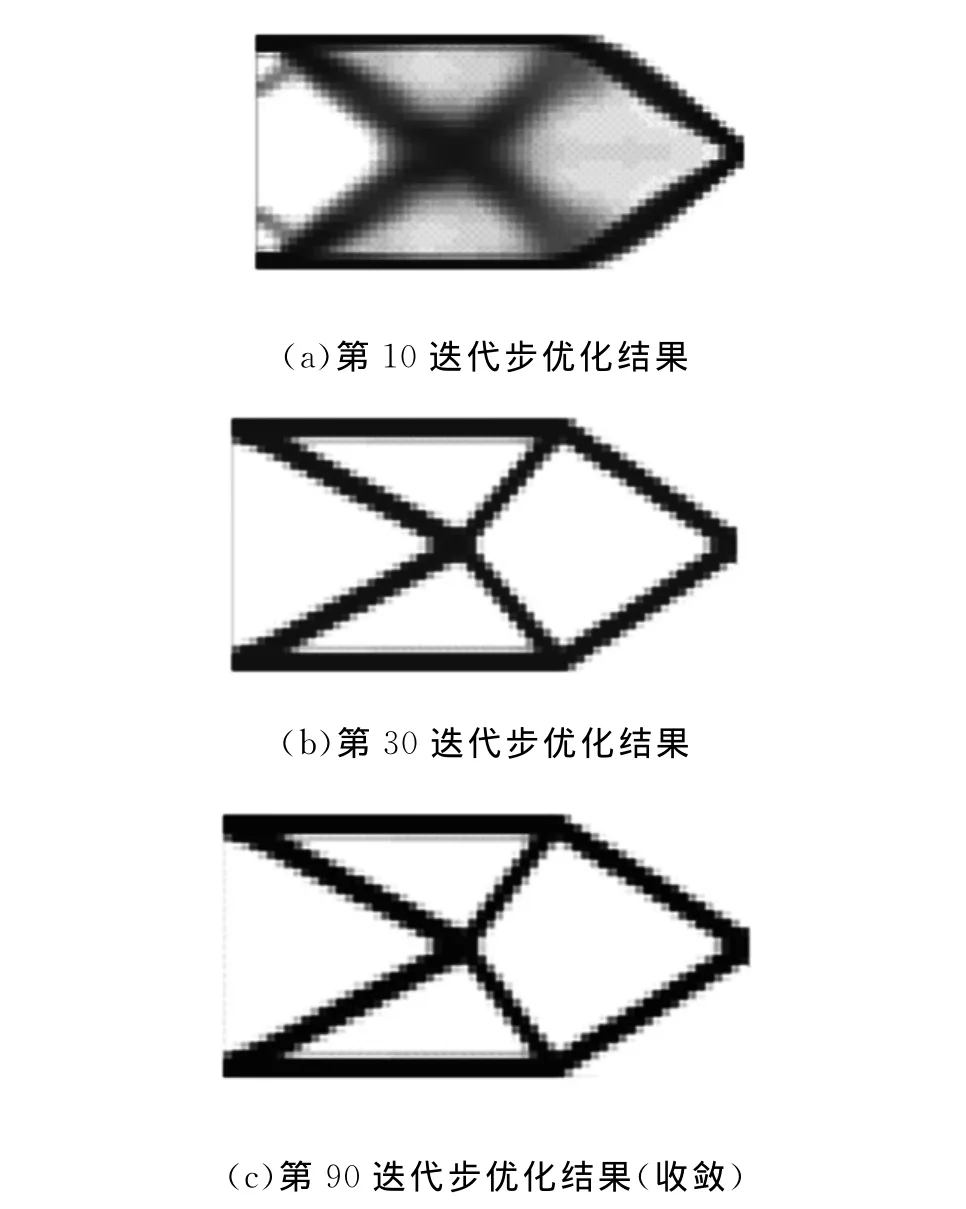
图2 双向插值区间敏度拓扑优化算法优化结果
3.2 MBB梁优化数值实现对比验证
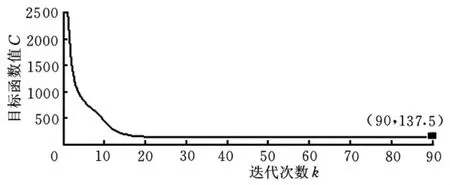
图3 目标函数收敛情况
MBB梁的拓扑优化在欧洲空中客车底扳支架设计中得到应用[9-11],MBB梁有各种不同的变化形式。如图4所示,一个边缘固定(不可设计)的简支梁,其内部为可设计区域,在规定载荷下以结构柔度最小化为目标函数的优化拓扑如图所示。应用本节区间敏度分析方法的优化结果如图5所示,表示结构优化边界由模糊逐渐变清晰过程。
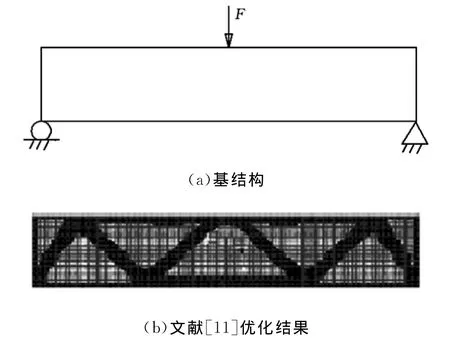
图4 MBB梁优化模型及优化结果
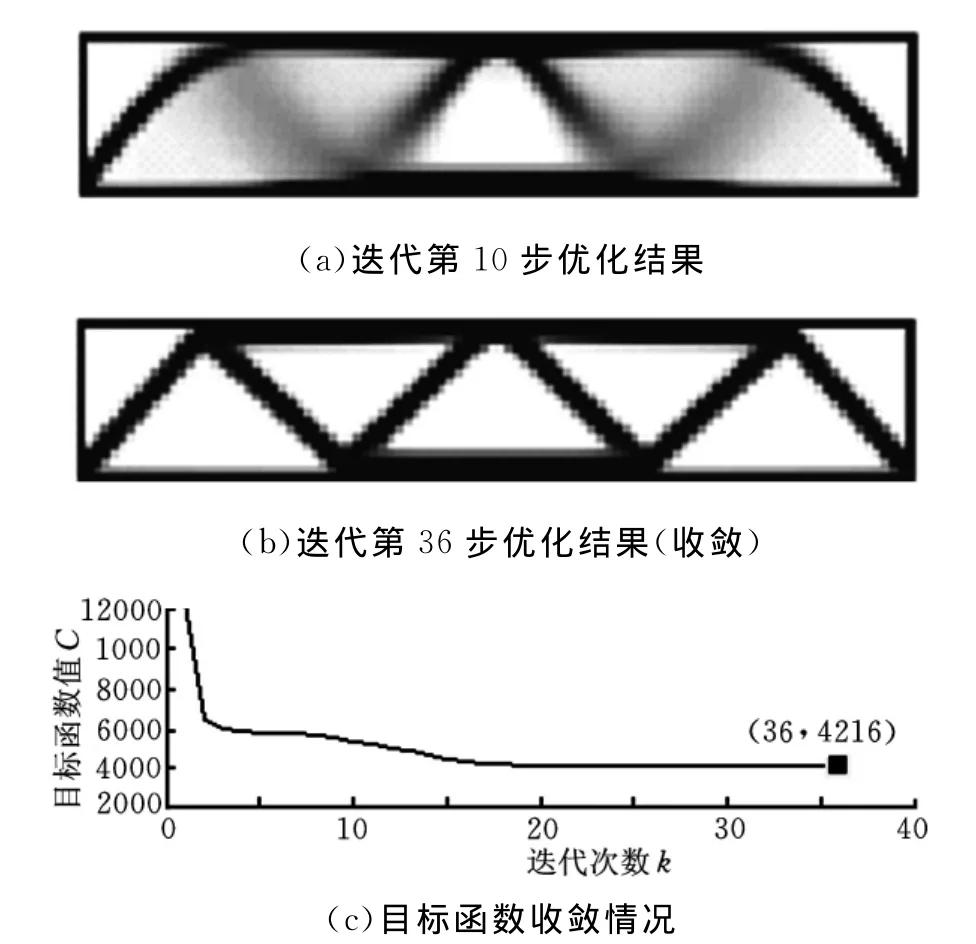
图5 MBB梁拓扑优化结果及目标函数迭代过程
上述算例数值结果表明,将区间分析方法应用到拓扑优化领域敏度分析中完全可行,结合双向插值模式的拓扑优化具有无需过滤、全局收敛和边界清晰的优点。
4 结语
本文研究区间分析方法特性,分析了区间分析方法在包含界约束拓扑优化问题中使用可行性;根据区间敏度分析优点与传统敏度分析的不足,将区间敏度分析思想引入结构拓扑优化设计,建立了子区间基(中心)移动拓扑优化方法,并用数值实验验证方法的正确性及实用性。本文结论为拓扑优化研究提供了一种新的研究思路和方法。
对于载荷等设计变量具有不确定性的结构,将区间分析方法与拓扑优化方法相结合,研究结构可靠性拓扑优化、结构失效模式拓扑优化、智能结构拓扑优化将是很有前景的研究课题。
[1]李新兰,姜潮,韩旭.基于区间的不确定多目标优化方法及应用[J].中国机械工程,2011,22(9):1100-1106.
[2]蔡新,昊威,昊黎华,等.土石坝结构区间优化设计河[J].河海大学学报,1998,26(3):1-5.
[3]李方义,李光耀,郑刚.基于区间的不确定多目标优化方法研究[J].固体力学学报,2010,31(1):86-93.
[4]吴杰.不确定参数结构的区间优化方法[J].机械设计与制造,2008(1):218-220.
[5]王海军,曹德欣,李苏北,等.非线性等式约束全局优化问题的区间算法[J].中国矿业大学学报,2003,32(2):204-208.
[6]邱志平,王晓军.结构灵敏度分析的区间方法[J].兵工学报,2005,26(6):798-802.
[7]邱志平,顾元宪.有界不确定参数结构位移范围的区间摄动法[J].应用力学学报,1999,16(1):1-10.
[8]邱志平,顾元宪.有界不确定性参数结构静力位移范围的区间参数摄动法[J].兵工学报,1998,19(3):255-258.
[9]Diaz A,Sigmund O.Checkerboard Patterns in Layout Optimization[J].Structural Optimization,1995,10:40-45.
[10]Jog C S,Haber R B.Stability of Finite Element Models for Distributed-parameter Optimization and Topology Design[J].Computer Methods in Applied Mechanics and Engineering,1996,130:203-226.
[11]Eschenauer H,Olhoff N.Topology Optimization of Continuum Structures:a Review[J].Appl.Mech.Rev.,2001,50(4):331-390.
