永磁直线同步电机一阶速度抗扰动控制

陈 冰 闫光亚 艾 武

1.华中科技大学，武汉，430074 2.北京航天控制仪器研究所，北京，100854

0 引言

永磁直线同步电机（PMLSM）系统是一种多变量、高非线性和强耦合系统，包括负载力、摩擦力、磁阻力等的多重扰动力直接作用于其动子上，使得传统控制方法难以解决其复杂的速度控制问题。一些针对PMLSM速度干扰问题的智能控制方法被提出。文献［1］提出了基于在线辨识补偿的PMLSM模型参考自适应神经网络速度控制方法，使得系统的自适应控制能力得到提高；文献［2］提出了一种基于模糊递阶理论的控制方法，提高了PMLSM控制系统的动静态特性；文献［3］利用神经网络实时补偿PMLSM端部效应对系统的扰动作用，给出了一种鲁棒性较强的基于双神经网络的前馈给定补偿IP复合控制策略；文献［4］将一种采用递归模糊神经网络（RFNN）的滑模控制器应用在PMLSM控制系统中，其递归模糊神经网络用来实时估计控制系统的不确定性并具有很好的鲁棒性；文献［5］利用神经网络辨识获取直线电机运动平台的非线性闭环系统模型并进行了系统的阶跃响应仿真。为了获得较好的系统动态性能和抗扰动能力，采用自抗扰控制技术来估计补偿不确定因素的控制方法被提出［6］，一些针对PMLSM扰动问题的控制策略也得到研究［7－11］。

本文根据PMLSM的运动方程设计了一种一阶速度抗扰动控制器，给出了控制器的详细结构框图和控制系统框图，提出了相应的控制算法，并在MATLAB/Simulink中建立了控制系统仿真模型，通过仿真与实验对控制系统进行了验证。

1 PMLSM速度扰动分析

PMLSM运行过程中，其动子会受到多重扰动力FΣ的直接作用，当高速运行时，以黏滞摩擦力为主的摩擦力为主要的扰动力；当低速运行时，磁阻力则成为主要的扰动力。多重扰动力FΣ可以表示为

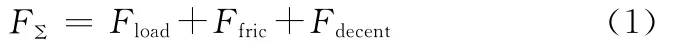
式中，Fload为负载力，Ffric为摩擦力，Fdecent为磁阻力。

PMLSM在d－q坐标系下的数学模型的运动方程可表示为

式中，v为直线电机动子运动速度；np为极对数；Ld、Lq分别为PMLSM直轴电感系数和交轴电感系数；id、iq分别为d、q轴电流；ψPM为永磁体磁链；m为动子质量；τ为定子永磁体极距；FΣ为动子受到的包括负载力、摩擦力和磁阻力在内的多重扰动力。

通过对PMLSM扰动力的分析，运动方程式（2）可以重新整理为

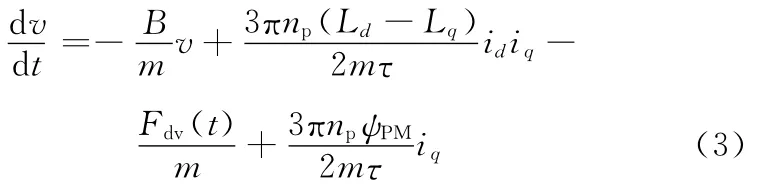
其中，B为黏滞摩擦系数，Fdv（t）为除去黏滞摩擦力之外的扰动力，即

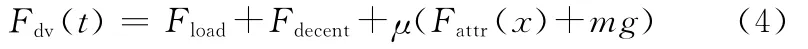
式中，μ为滑动摩擦系数；Fattr为永磁体对初级铁芯的法向吸引力。

式（3）中的第一项－Bv/m可被视为由速度v引起的黏滞摩擦力对动子运动速度动态过程的内部确定性扰动，记为f0v（v）；由于电流环采用的是＝0的解耦控制，所以式（3）中等号右边的第二项3πnp（Ld－Lq）idiq/（2mτ）在理想情况下为0，但实际上Ld和Lq不可能完全相等，同时id会因为动态误差而不为0，所以式（3）中等号右边的第二项会存在一个比较小的不为0的值，从而对PMLSM的速度动态过程造成影响，这一项可被视为由id和iq对PMLSM速度动态特性施加的外部未知扰动，记为dv1（t）；式（3）中等号右边第三项－Fdv（t）/m为动子所受负载力、磁阻力、滑动摩擦力等对PMLSM速度动态特性的外部未知扰动，记为dv2（t）。则式（3）可以重新写为

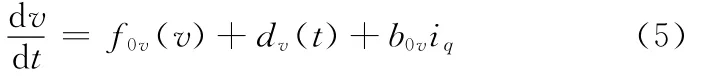
其中

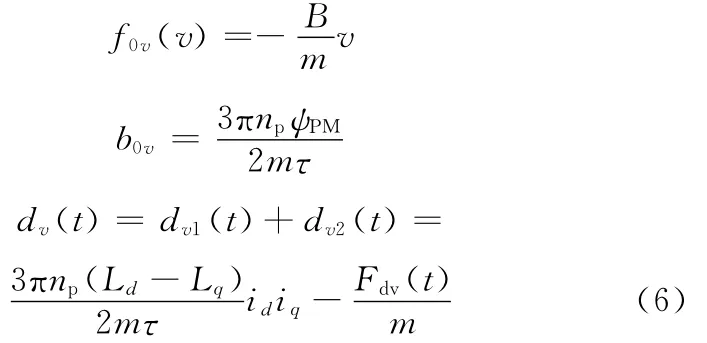
2 一阶速度抗扰动控制系统

对于式（5）所描述的一阶速度动态过程，应用改进型抗扰动控制算法设计了PMLSM的一阶速度抗扰动控制系统，控制系统的原理如图1所示。

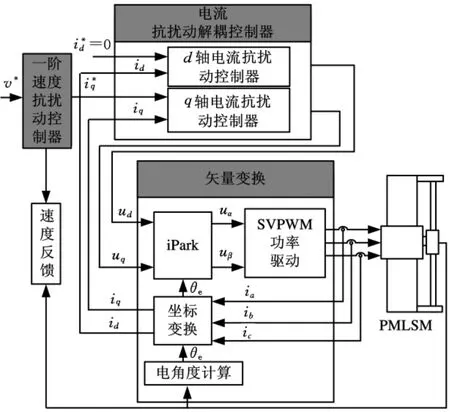
图1 PMLSM一阶速度抗扰动控制系统结构

PMLSM运行时存在机械惯性，其速度不可能突变，但是对于PMLSM控制系统指令而言会存在突变或者变化极快的速度给定值，如果直接取速度给定值和反馈值之间的误差，则在初始时刻会出现比较大的误差，控制器的输出控制量会过大，造成PMLSM运动速度超调和振荡。本文的一阶速度抗扰动控制器利用前向通道的跟踪微分器［12］（TD）生成一个速度给定量的过渡过程，起到 “柔化”速度给定值的作用，从而很好地解决了速度响应的快速性和超调性之间的矛盾。除了上述前向通道跟踪微分器，本文的一阶速度抗扰动控制器还包含反馈通道的跟踪微分器、扩张状态观测器（ESO）、非线性状态误差反馈（NLSEF），其具体结构框图见图2。

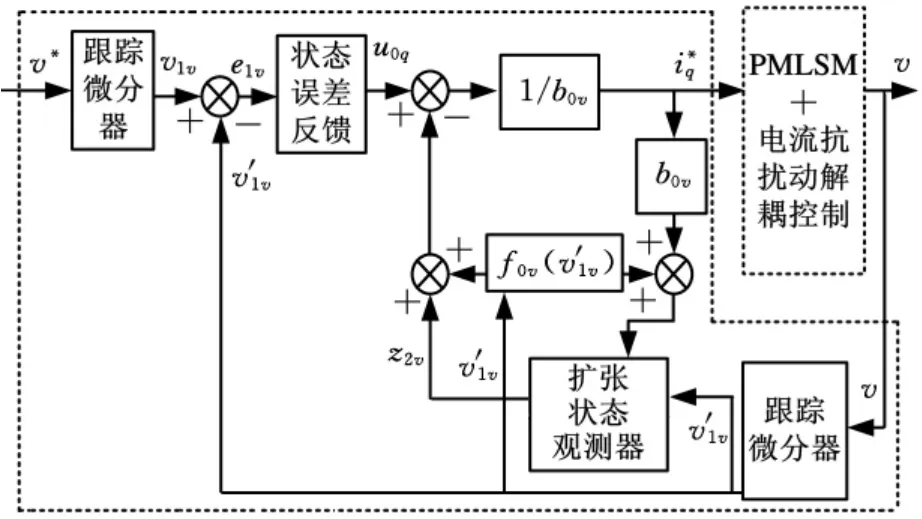
图2 一阶速度抗扰动控制器结构框图

一阶速度抗扰动控制器中的扩张状态观测器可以观测出多重扰动力作用于PMLSM速度动态过程的外部未知扰动dv（t），即观测器输出z2v→dv（t）；反馈 通 道 的 跟 踪 微 分 器 能 够 得 到PMLSM的实际速度，即观测器输出v′1v→v。取电流控制量：

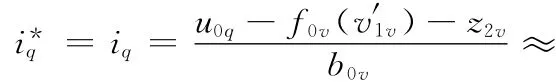
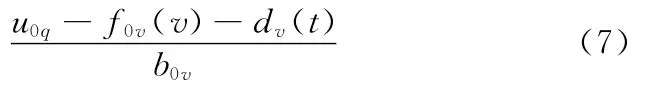
式中，u0q为q轴反馈控制量。

将式（7）代入式（5）所描述的一阶速度动态过程，可得

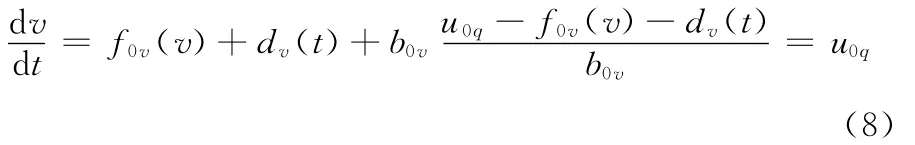
可见，一阶速度抗扰动控制器把PMLSM的速度动态过程改造成为纯积分环节，并利用非线性状态误差反馈实现PMLSM的一阶速度抗扰动控制。

由抗扰动控制算法［6－9］和PMLSM 的速度一阶动态过程式（5）和式（6），可以得出一阶速度抗扰动控制器如下：

前向通道跟踪微分器

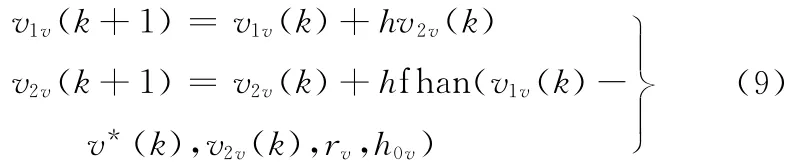
反馈通道跟踪微分器

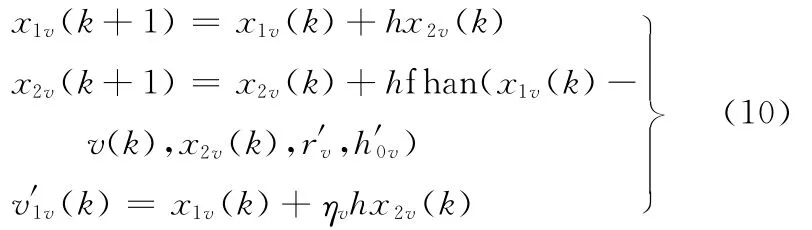
扩张状态观测器

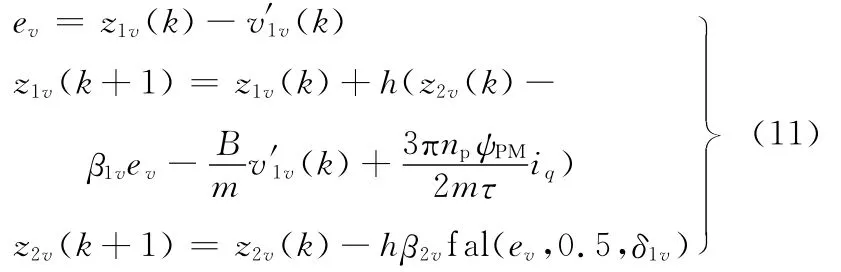
非线性状态误差反馈

动态扰动补偿

其中，h为计算步长；rv为前向通道跟踪微分器的跟踪速度因子；h0v为滤波因子；r′v为反馈通道跟踪微分器的跟踪速度因子；h′0v为滤波因子；ηv为预报步长因子；fhan（·）为离散域最速控制综合函数［6］。

式（11）、式（12）中，β1v和β2v为扩张状态观测器的反馈系数，δ1v为其中fal函数的参数；kv为非线性状态误差反馈的反馈系数，αv和δ2v为其中fal函数的参数。对于S型非线性函数fal（e，α，δ）（δ为零点对称线性区间的长度，α为对应线性区间的逆斜率），当0＜α＜1时，fal函数具有“小误差，大增益；大误差，小增益”的特征，且α越小，该特征越明显，较适合于作为误差反馈控制律。

3 仿真结果

为了验证一阶速度抗扰动控制系统的效果，在MATLAB/Simulink中进行了仿真实验，仿真模型如图3所示，其中一阶速度抗扰动控制器的仿真模型如图4所示。

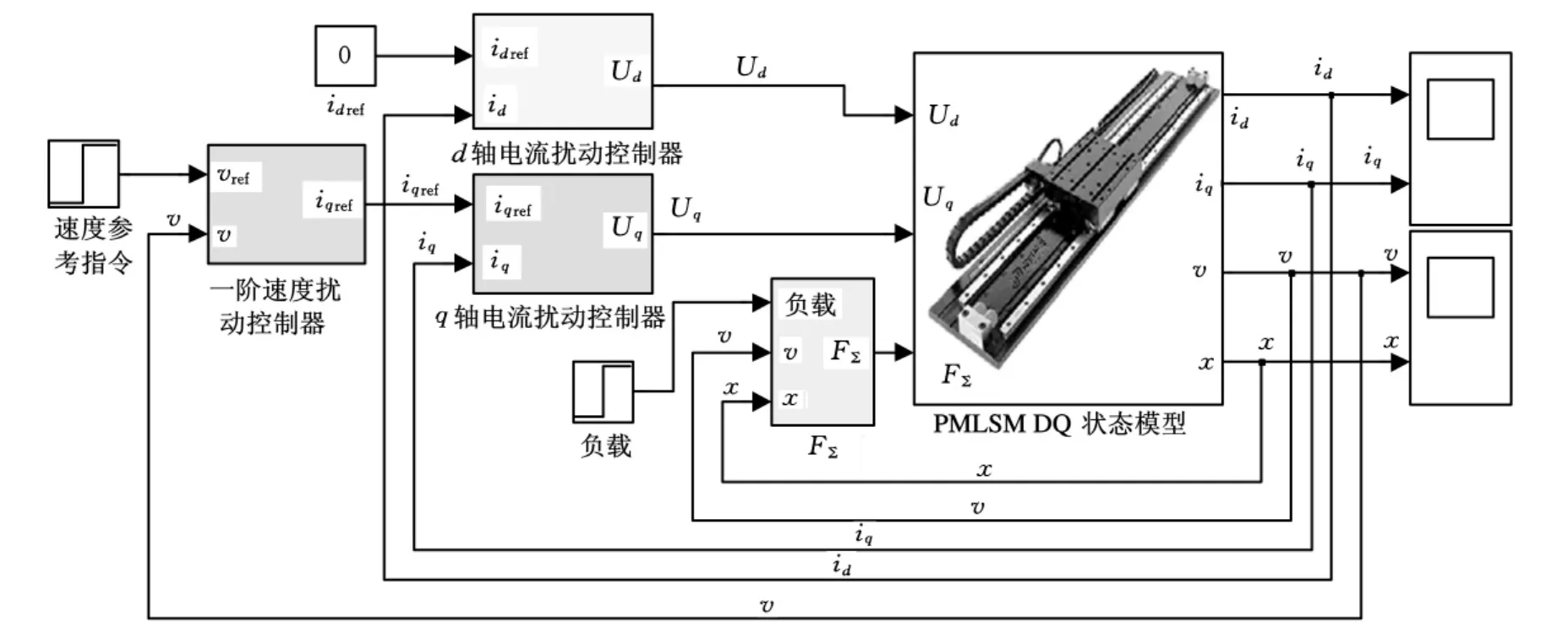
图3 一阶速度抗扰动控制系统仿真模型

为了加快q轴电流的响应速度，在该仿真模型中省去了q轴电流抗扰动控制器中的跟踪微分器；由于d轴电流给定量i＊d恒为0，所以也省去了d轴电流抗扰动控制器中的跟踪微分器。PMLSM的参数为实验样机的实际参数。根据抗扰动控制器参数选取要求，经过多次仿真实验，确定的图3中各抗扰动控制器的参数列于表1中，计算步长h＝10－4。

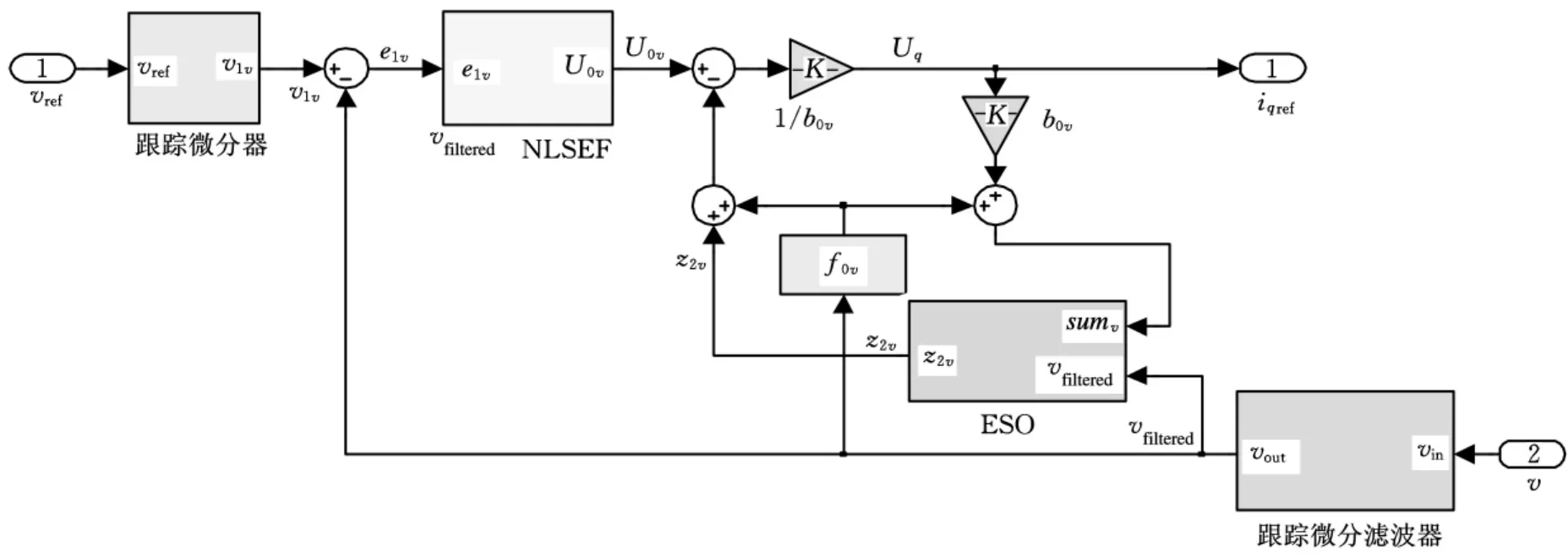
图4 一阶速度抗扰动控制器的仿真模型

表1 PMLSM一阶速度抗扰动控制系统中各控制器的参数

在仿真实验中，速度给定值为单位阶跃输入，PMLSM空载启动，在0.5s时突加200N负载，同时考虑摩擦力和磁阻力扰动，得到的一阶速度抗扰动控制系统的仿真结果如图5～图10所示。

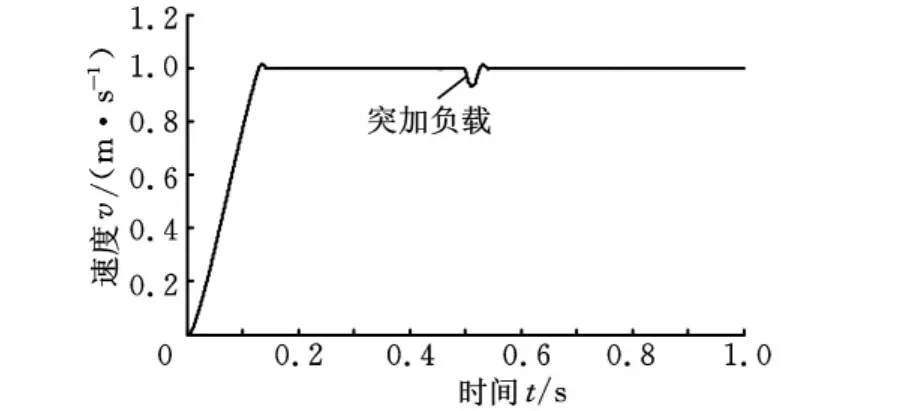
图5 速度响应

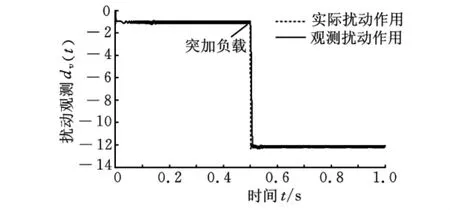
图6 扰动作用dv（t）观测

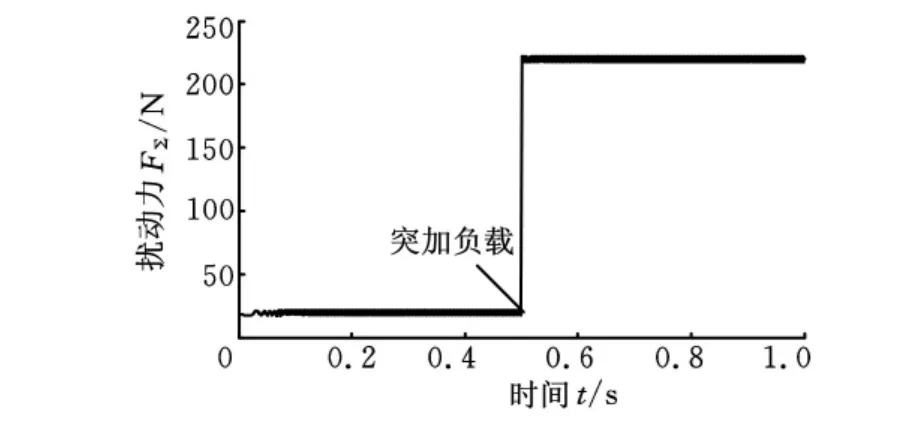
图7 PMLSM受到的扰动力

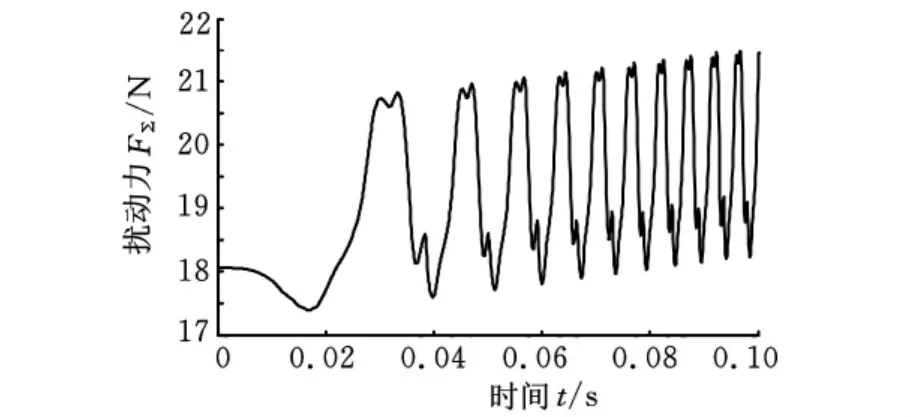
图8 图7中扰动力的放大曲线

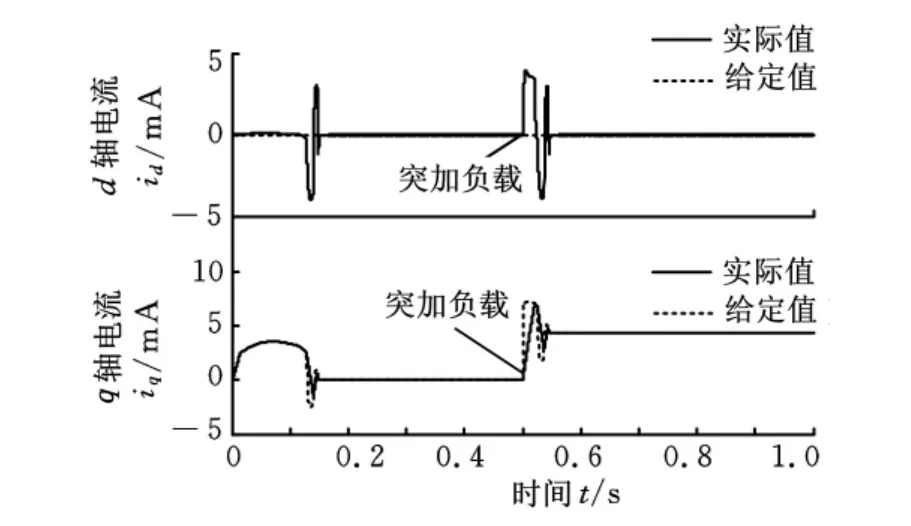
图9 d－q轴电流波形

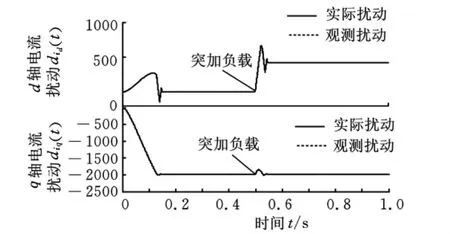
图10 d－q轴电流耦合扰动观测

由图5可以看出，在一阶速度抗扰动控制器的控制作用下，PMLSM的速度在0.13s左右达到1m/s的给定值，动态响应快，超调量非常小，仅为0.015m/s；当突加负载时，PMLSM 的速度仅下降0.07m/s，波动量小，并在0.05s内快速恢复至v＝1m/s。图6为扩张状态观测器的扰动作用观测曲线，可见扩张状态观测器能很好地观测出负载力、摩擦力和磁阻力对PMLSM造成的扰动作用dv（t），这是实施抗扰动控制的关键。图7是PMLSM受到的包括负载力、摩擦力和磁阻力在内的扰动力FΣ，图9和图10是d－q轴电流抗扰动解耦控制的仿真结果，容易看出，d－q轴电流抗扰动解耦控制器中的扩张状态观测器都能观测出d－q轴电流的耦合扰动，并且d－q轴电流的稳态误差为0，但存在一定的动态误差，在一阶速度抗扰动中，认为i＊q＝iq，这个动态误差会影响一阶速度抗扰动的控制效果。

4 实验与分析

PMLSM一阶速度抗扰动控制系统实验平台由PMLSM、控制板、驱动板、PWM数模转换板、限位开关以及示波器组成，其结构如图11所示。本文中PMLSM的电气参数如表2所示。

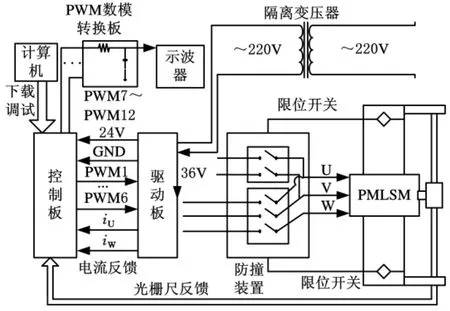
图11 PMLSM一阶速度扰动控制系统实验平台

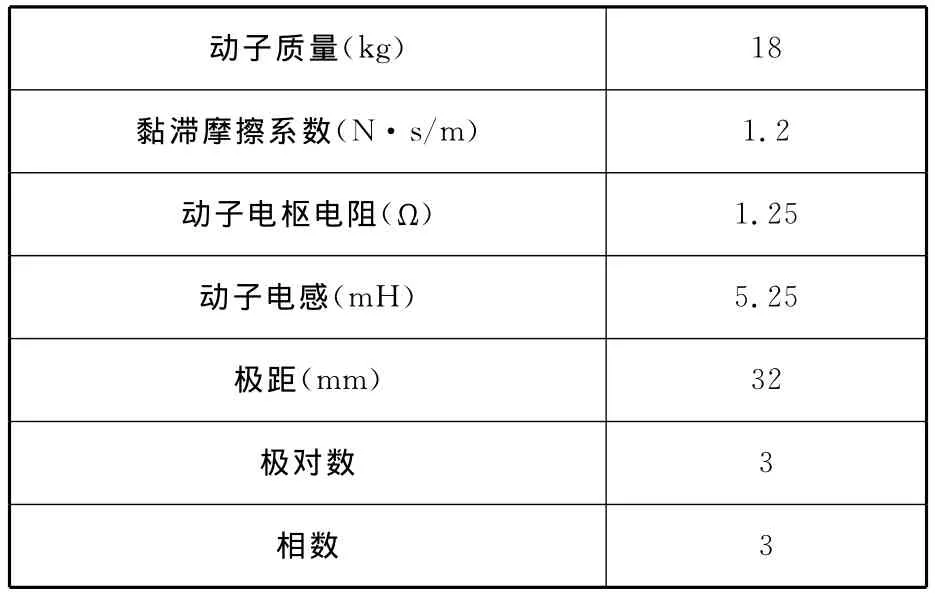
表2 PMLSM电气参数

应用设计的PMLSM一阶速度抗扰动控制器对PMLSM的一阶速度抗扰动控制系统进行了实验，为了和同类型的控制方法相比较，对采用PID控制的PMLSM速度控制系统做了实验对比研究。实验中的数据同样均先利用DSP调制成PWM波，然后经过PWM数模转换板转化为模拟量，最后用示波器测量出来。同时为了验证PMLSM速度抗扰动控制系统对负载扰动的“抗扰”能力，对PMLSM进行了突加负载50N的试验。给定0.5m/s的阶跃速度指令，分别采用PID控制、一阶速度抗扰动控制得到的速度响应曲线分别如图12a、图12b所示。

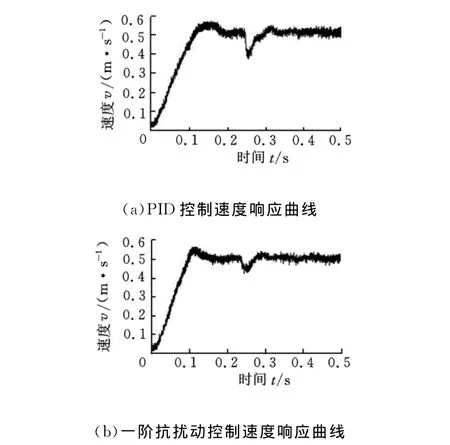
图12 两类速度抗扰动控制动态特性实验响应曲线

从图12可以看出，两种控制方法都能获得比较好的速度稳态精度，但在动态特性和抗扰能力上有较明显的差别。采用PID控制时，PMLSM的响应时间相对比较慢，大约在0.2s左右进入稳态阶段，而且存在约10%的超调量，当突加负载时PMLSM出现比较大的速降，速度降低了约20%；采用一阶速度抗扰动控制时，PMLSM的阶跃速度响应在快速性和抗负载扰动能力上都比PID算法强，调节时间缩短为0.15s左右，速降为13%左右。

5 结语

本文针对多重扰动力对PMLSM的动态过程造成的影响给出了一种PMLSM一阶速度抗扰动控制系统，基于扩张状态观测器（ESO）观测出多重扰动力对PMLSM的速度动态过程的扰动作用，通过动态扰动补偿装置（DEC）对这个扰动作用进行补偿，进而实现PMLSM一阶速度抗扰动控制。根据PMLSM的运动方程设计了一阶速度抗扰动控制器，在MATLAB/Simulink中建立了控制系统仿真模型，通过仿真分析并且与PID算法进行对比实验验证，结果表明PMLSM一阶速度抗扰动的控制效果良好。

［1］郭庆鼎，王军.基于在线辨识补偿的永磁直线同步电机模型参考自适应神经网络速度控制［J］.电气传动，2000（4）：16－19.

［2］Ai Wu，Du Zhiqiang，Tam P K，et al.Hierarchical Fuzzy Neural Controller Based on Error Iterative and Approach［C］//Proceedings of the Second International Conference on Machine Learning and Cybernetics.Xi’an，2003：1299－1303.

［3］Guo B Z，Han J Q，Xi F B.Linear Tracking－differentiator and Application to Online Estimation of the Frequency of a Sinusoidal Signal with Random Noise Perturbation［J］.International Journal of System Science，2002，33（5）：351－358.

［4］张纯明，郭庆鼎.基于反馈线性化的交流直线永磁同步伺服电机速度跟踪控制［J］.电工技术学报，2003，18（3）：5－9.

［5］夏加宽，王成元，李皞东，等.高精度数控机床用直线电机端部效应分析及神经网络补偿技术［J］.中国电机工程学报，2003，23（8）：100－104.

［6］韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术［M］.北京：国防工业出版社，2008.

［7］Choi Chintae，Tsao Tsu－Chin.Control of Linear Motor Machine Tool Feed Drives for End Milling：Robust MIMO Approach［J］.Mechatronics，2005，15：1207－1224.

［8］Lin Faajeng，Shyu Kuokai，Lin Chihhong.Incremental Motion Control of Linear Synchronous Motor［J］.IEEE Transactions on Aerospace and Electronic Systems，2002，38（3）：1011－1022.

［9］崔丽丽，刘栋良.全数字交流伺服系统及其控制策略综述［J］.伺服控制，2007（3）：16－18.

［10］Gordon S，Hillery M T.Development of a Highspeed CNC Cutting Machine Using Linear Motors［J］.Journal of Materials Processing Technology，2005，166：321－329.

［11］Yang Junyou，Chen Ruijuan，Fa Naiguang.A New Recurrent Fuzzy Neural Network Sliding Mode Position Controller Based on Vector Control of PMLSM Using SVM［C］//CES/IEEE 5th International Power Electronics and Motion Control Conference.Shanghai，2006：1－5.

［12］韩京清，袁露林.跟踪－微分器的离散形式［J］.系统科学与数学，1999，19（3）：268－273.