基于H2／H∞控制的汽车主动悬架最优鲁棒容错控制

杨柳青 陈无畏 汪洪波

1.合肥工业大学，合肥，230009 2.安徽交通职业技术学院，合肥，230051

基于H2／H∞控制的汽车主动悬架最优鲁棒容错控制

杨柳青1，2陈无畏1汪洪波1

1.合肥工业大学，合肥，230009 2.安徽交通职业技术学院，合肥，230051

为提高汽车主动悬架控制可靠性和控制效果，针对悬架参数摄动和作动器故障，提出一种基于H2／H∞的最优鲁棒容错控制方法。考虑作动器常见故障、悬架刚度与阻尼系数摄动，建立故障悬架模型。基于H2／H∞状态反馈控制，利用有界实引定理推导出悬架最优鲁棒容错控制器设计条件。运用LMI工具箱离线设计控制器，并在MATLAB／Simulink环境下进行大量仿真计算。结果表明，设计的最优鲁棒容错控制器能改善汽车主动悬架乘坐舒适性，亦能改善故障悬架乘坐舒适性，且在控制效果上均优于完好无故障状态下设计的控制器。

汽车主动悬架；鲁棒容错控制；参数摄动；作动器故障

0 引言

容错控制（fault tolerant control，FTC）在系统部件发生故障时仍能维持系统性能或维持其性能在可接受的范围内。汽车主动悬架系统（active suspension system，ASS）由汽车悬架、传感器、控制器和作动器组成。目前，对汽车悬架系统控制的研究均是建立在各元部件完好的基础之上而进行的［1－3］，研 究 成 果 能 明 显 改 善 被 动 悬 架 系 统（passive suspension system，PSS）的性能。但是，元器件老化、疲劳等将导致系统参数发生摄动，使系统中的传感器或作动器发生故障，这些都将造成假定各元部件完好的情况下设计的控制器误控制，达不到预期控制效果，甚至出现控制效果部分或全部丧失的情况，影响汽车乘坐舒适性。因此，对汽车主动悬架进行容错控制是进一步提升其控制可靠性的有效方法。被动容错控制（passive fault tolerant control，PFTC）是一类有效容错控制方法，它事先考虑汽车主动悬架故障，离线设计控制器，因而使系统对故障不敏感，从而提高控制可靠性和控制效果。

文献［4］基于作动器和传感器完好，且未考虑参数摄动，对七自由度整车悬架进行了H2／H∞多目标控制。文献［5］仅考虑二自由度四分之一悬架模型参数不确定性，对悬架系统进行保性能控制。文献［6］在液压作动器故障诊断基础上对汽车液压悬架进行了主动容错控制。文献［7］也在故障检测与隔离的基础上，考虑线性参数时变模型，对悬架系统进行主动容错控制。这种主动容错控制均需要及时准确的故障诊断与检测机构。

在控制器设计之初，预先考虑汽车主动悬架作动器故障和系统参数摄动对悬架系统进行被动容错控制，是一种简单实用的可靠方法，目前尚无文献涉及。基于此，本文采用七自由度整车悬架模型，考虑汽车主动悬架刚度和阻尼系数两参数摄动及其作动器增益损失故障，建立故障悬架模型。基于多目标H2／H∞状态反馈控制，运用线性矩阵不等式（LMI）方法设计闭环系统最优鲁棒容错控制器，在MATLAB中进行大量仿真实验与分析。

1 系统建模

1.1 七自由度汽车主动悬架模型

考虑车身垂向、俯仰、侧倾运动及非簧载质量垂向运动，建立七自由度汽车主动悬架动力学模型［8－9］，如图1所示。

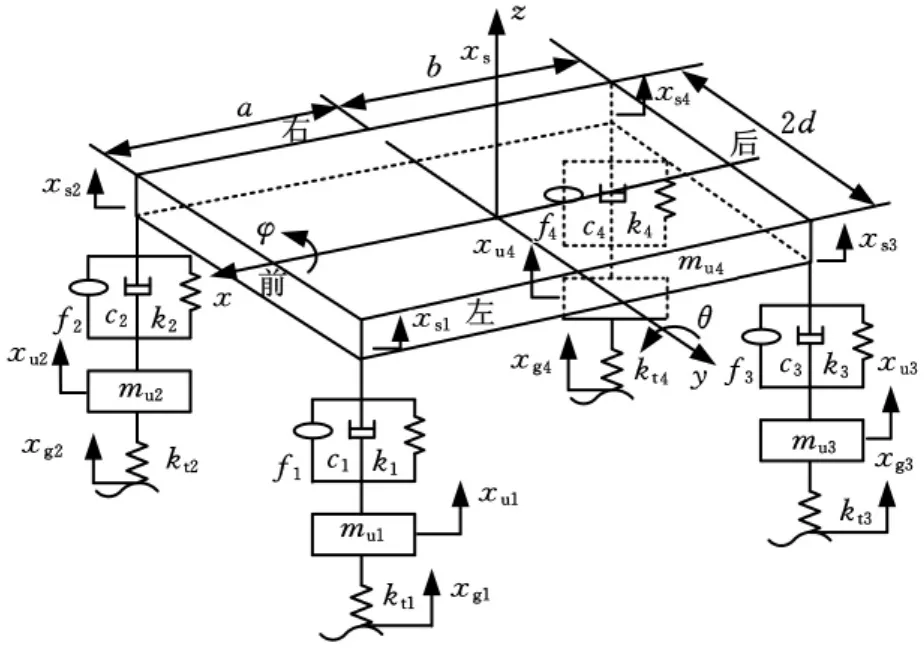
图1 七自由度汽车主动悬架模型

车身垂向、俯仰、侧倾运动方程为

其中，xsui＝xsi－xui（i＝1，2，3，4）为悬架动挠度，rmax为悬架动挠度最大限值，fmax为作动器控制输出力最大限值。

建立七自由度整车主动悬架系统状态方程和控制输出方程如下：

其中，A为14×14矩阵；B1为14×4矩阵；B2为14×4矩阵；C1为8×14矩阵；C2为3×14矩阵；D12为8×4矩阵；D22为3×4矩阵。

1.2 故障悬架模型

在实际使用中，随着汽车行驶里程的增加，汽车主动悬架刚度、阻尼系数会发生一定范围的摄动，导致汽车主动悬架系统具有一定的不确定性。假设汽车主动悬架系统不确定性具有如下结构［11］：

其中，ΔA、ΔB2为汽车主动悬架因参数摄动而导致 的 不 确 定 量；H、E1、E2是 适 维 常 量 矩 阵；F∈L2［0，＋∞）为范数有界矩阵函数，满足

式中，I为维数适当的单位矩阵。

考虑汽车主动悬架作动器一般多为液压伺服机构，液压油缸或液压油管中液压油泄漏等将导致液压作动器控制输出力出现增益损失，所以不失一般性，本文仅考虑汽车主动悬架作动器发生增益损失故障［7］。设反映左前、右前、左后、右后4个位置的作动器增益损失故障程度大小的故障增益分别为δ1、δ2、δ3、δ4，则汽车主动悬架作动器故障控制输出Uf为

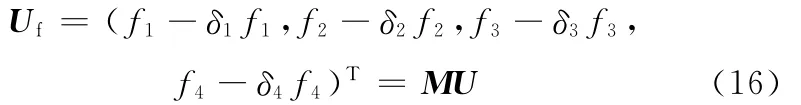
其中，M为因作动器故障而形成的故障开关矩阵［12］：

因而，考虑作动器故障，同时将因参数摄动而导致的系统不确定量引入汽车主动悬架系统，故障悬架系统（fault active suspension systems，FASS）的状态方程和控制输出方程为

2 汽车主动悬架控制

选取某型汽车悬架参数值如表1［13，4］所示。

车辆以速度v＝15m／s经过B级路面，路面不平度系数G0＝64×10－6m3，下截止频率f0＝0.1Hz。汽车主动悬架采用H2／H∞状态反馈控制，利用 MATLAB／Simulink进行仿真，获得具有良好控制性能的闭环控制器。在LMI工具箱中利用命令msfsyn可求状态反馈增益矩阵Kn。U＝KnX为各元部件完好无故障状态下设计的正常H2／H∞状态反馈控制器输出向量。

表1 汽车主动悬架模型参数

当作动器发生增益损失故障及悬架参数有摄动时，在正常H2／H∞状态反馈控制器控制下的故障悬架系统（简记为FASS／N）性能将变差，达不到预期控制效果。

3 最优鲁棒容错控制器设计

汽车主动悬架鲁棒容错控制（robust fault tolerant control，RFTC）设计目的是，在控制器设计之初事先考虑作动器故障和悬架系统参数摄动，使设计的鲁棒容错控制器不仅对完好无故障汽车主动悬架控制（简记为ASS／RFTC）具有良好的控制效果，或与正常H2／H∞状态反馈控制器控制下的汽车主动悬架（简记为ASS／N）具有相接近的性能指标，而且对发生参数摄动和作动器故障的故障悬架控制（简记为FASS／RFTC），仍具有较好的控制效果，使悬架控制在故障情况下具有容错控制效果和一定的鲁棒性，从而实现汽车主动悬架的鲁棒容错控制。

设计的状态反馈最优鲁棒容错控制器为

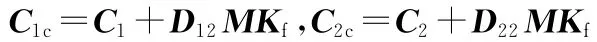
上述故障闭环系统需满足以下设计目标：①故障闭环系统渐近稳定；②从干扰输入W到控制输出Z∞的闭环传递函数‖Twz∞（s）‖∞＜γ；③故障闭环系统的H2性能指标R（Kf）＝suplimE｛Z2TZ2｝≤（Kf），其中，E｛·｝表示矩阵期望算子。

根据多目标H2／H∞控制和有界实引定理［11］知，当且仅当下面的矩阵不等式

再将故障开关矩阵式（18）代入式（31），考虑式（19）条件，再次应用文献［11］中引理和Schur补性质，存在一很小正数η＞0使下式成立：

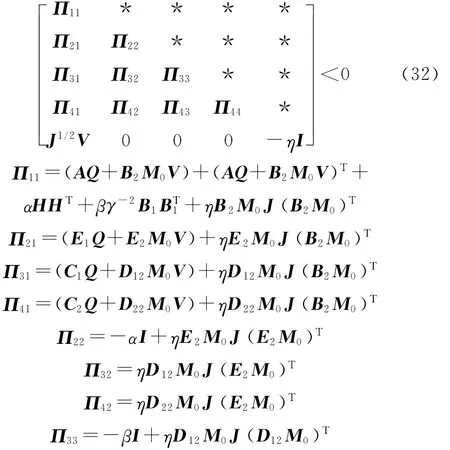
考虑故障闭环系统H2性能指标值满足R（Kf）≤tr（BT1Q－1B1），通过下列具有约束条件的不等式可求得闭环系统H2／H∞状态反馈最优鲁棒容错控制律：

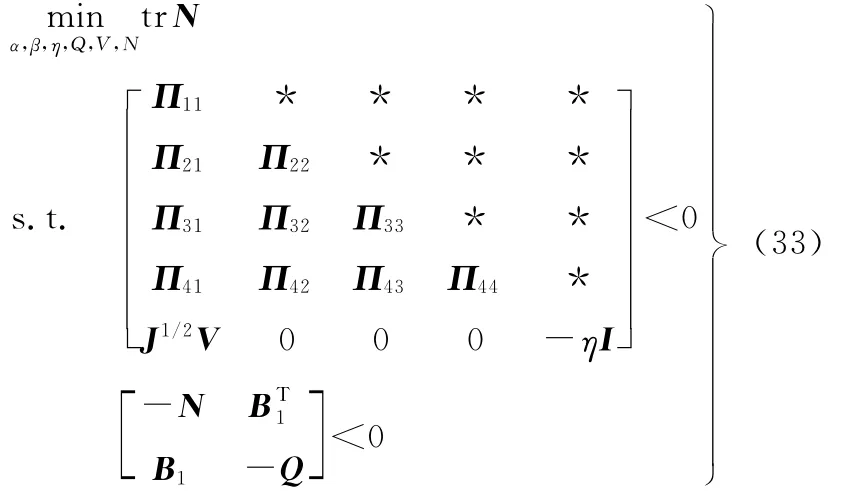
给定干扰抑制度γ＞0，应用LMI工具箱求解器 mincx可得式（33）最优解［11］：α＊、β＊、η＊、Q＊、V＊、N＊。故障闭环系统H2／H∞状态反馈最优鲁棒容错控制律为

汽车主动悬架刚度摄动和阻尼系数摄动均按±20%范围考虑，且按正弦函数规律变化［5］。利用式（14）借助 MATLAB计算，取

在MATLAB中经验证，故障悬架能控能观。取干扰输入W到控制输出Z∞闭环传递函数H∞性能指标γ＞1.75，求得故障闭环系统H2／H∞状态反馈最优鲁棒容错控制律Kf为

4 仿真实验结果与分析

汽车主动悬架在实际使用中会处于完好无故障和故障两种状态，因而从两种实际使用状态考虑，通过仿真实验进行控制效果分析。

4.1 汽车主动悬架控制结果与分析

汽车主动悬架在正常H2／H∞状态反馈控制律和最优鲁棒容错控制律控制下，各性能指标响应对比如图2～图8所示。

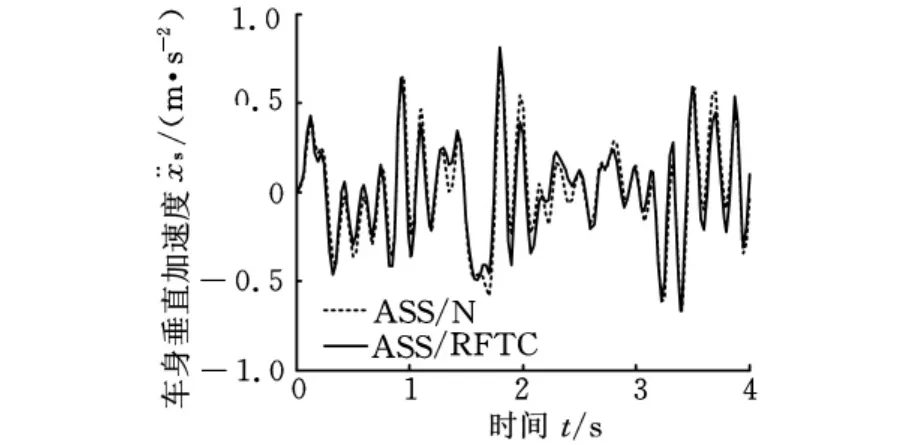
图2 完好无故障状态车身垂直加速度响应

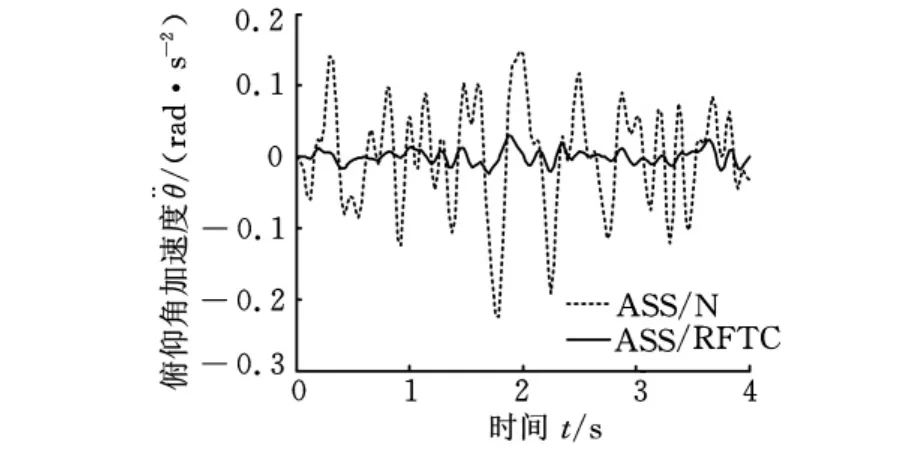
图3 完好无故障状态俯仰角加速度响应

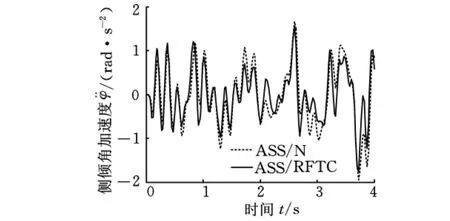
图4 完好无故障状态侧倾角加速度响应

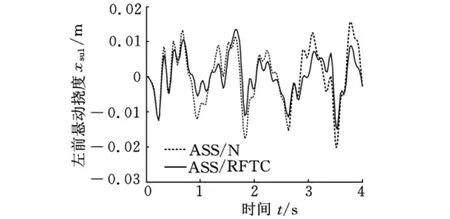
图5 完好无故障状态左前悬动挠度响应

由图2可以看出，汽车主动悬架在最优鲁棒容错控制律控制下，车身垂直加速度响应同完好无故障状态时设计的正常H2／H∞状态反馈控制器控制下的响应具有相同的效果，能改善汽车悬架行驶平顺性，而且，两种控制律控制下的性能响应较为接近，达到了良好的控制效果。

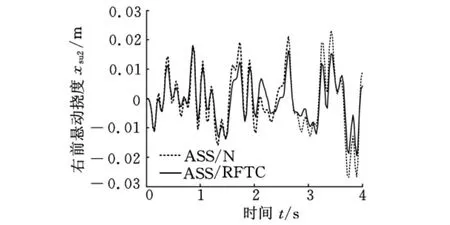
图6 完好无故障状态右前悬动挠度响应

图7 完好无故障状态左后悬动挠度响应

图8 完好无故障状态右后悬动挠度响应

由图3可以看出，在最优鲁棒容错控制律控制下，俯仰角加速度的控制不仅与完好无故障状态下设计的正常H2／H∞状态反馈控制器具有相同的效果，能明显改善悬架性能，而且在控制效果上还优于正常H2／H∞状态反馈控制器控制下的效果。同样，由图4～图8亦可清晰地看出，在最优鲁棒容错控制律控制下，侧倾角加速度、悬架动挠度性能指标的控制效果也均优于正常H2／H∞状态反馈控制器控制下的效果，同时与正常H2／H∞状态反馈控制律一样，能明显改善悬架乘坐舒适性能。

应用最优鲁棒容错控制律Kf对汽车主动悬架进行控制后，由仿真结果可看出：相对于被动悬架，最优鲁棒容错控制律能较好地控制车身姿态，使乘坐舒适性达到良好的控制效果；同时将最优鲁棒容错控制律控制的性能响应与完好无故障状态下设计的控制器控制的性能响应进行比较，在控制效果上前者接近或优于后者。

4.2 故障悬架容错控制结果与分析

假设故障1为悬架刚度摄动和阻尼系数摄动均为－10%，第1个（左前）作动器在时间t＝1s时发生故障增益δ1＝0.6的故障；故障2为悬架刚度摄动和阻尼系数摄动均为－15%，在t＝1s时第1个（左前）作动器发生故障增益δ1＝0.6，第3个（左后）作动器也发生故障增益为δ3＝0.6的故障；故障3为悬架刚度摄动和阻尼系数摄动均为＋10%，在t＝0.5s时，第1个（左前）作动器发生故障增益δ1＝0.6的故障，第2个（右前）作动器发生故障增益δ2＝0.3的故障，第3个（左后）作动器发生故障增益δ3＝0.3的故障，第4个（右后）作动器发生故障增益δ4＝0.4的故障。

基于上述三种故障事例进行仿真实验。正常H2／H∞状态反馈控制器控制下的故障悬架、最优鲁棒容错控制律控制下的故障悬架各性能响应对比如图9～图15所示（考虑篇幅，列出了几个代表性的性能响应图）。

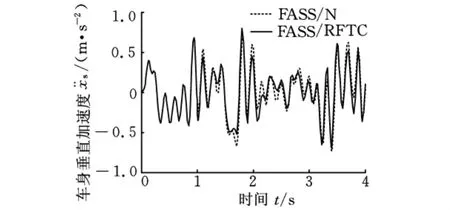
图9 故障1状态车身垂直加速度响应

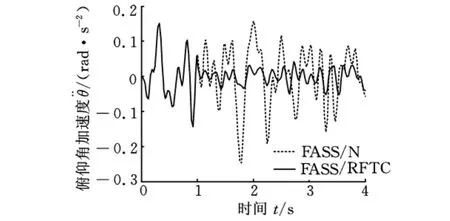
图10 故障1状态俯仰角加速度响应

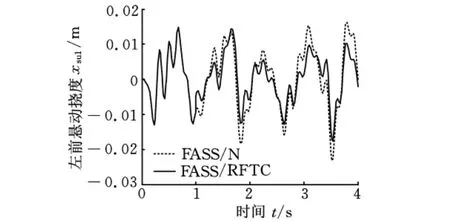
图11 故障1状态左前悬动挠度响应

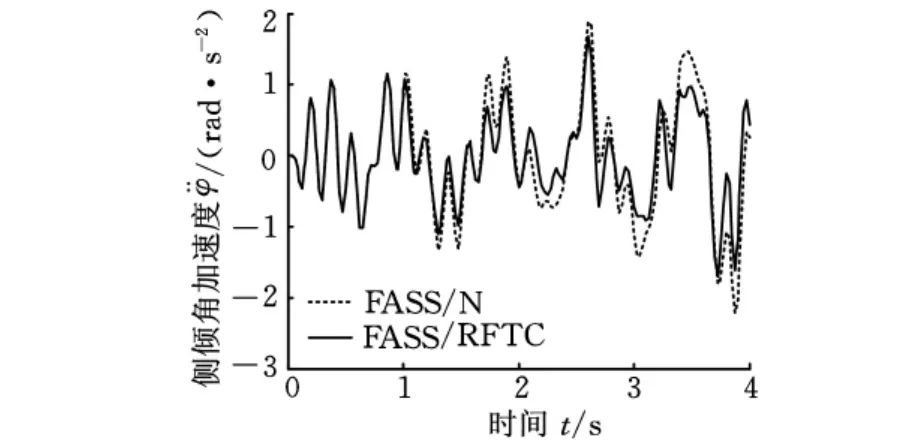
图12 故障2状态侧倾角加速度响应

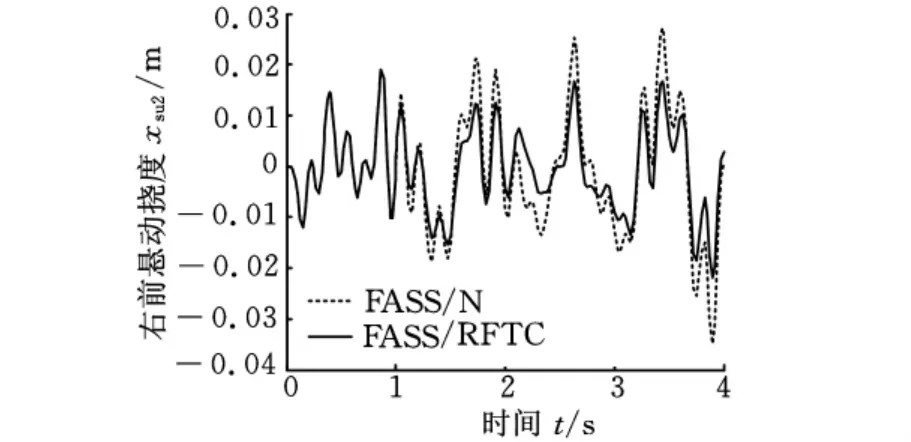
图13 故障2状态右前悬动挠度响应

图14 故障3状态俯仰角加速度响应

由图9～图11可以看出，故障悬架处于故障1状态时，在故障时刻t＝1s汽车前主动悬架采用正常H2／H∞状态反馈控制器，控制效果正常。而故障时刻t＝1s后，若仍采用正常H2／H∞状态反馈控制器，由于作动器故障和参数摄动的原因，车身垂直加速度、俯仰角加速度、左前悬动挠度等性能指标开始出现波动，控制效果变差，如图中虚线部分所示。经仿真数据计算，左前悬动挠度、侧倾角加速度、右后悬动挠度的均方根值波动量分别达12.7%、11.8%、10.99%。而在故障时刻t＝1s后若采用最优鲁棒容错控制律，故障悬架的车身垂直加速度、俯仰角加速度、悬架动挠度性能得到很好的控制，而且控制效果优于正常H2／H∞状态反馈控制器控制下的控制效果，如图中实线部分所示。

同样，从图12～图15亦可显然看出，当故障悬架分别处于故障2或故障3状态时，故障发生时刻t＝1s或t＝0.5s后在最优鲁棒容错控制律控制下，其各项性能控制均能达到很好的控制效果，且性能均优于正常H2／H∞状态反馈控制器控制下的性能。

两种控制律控制下的故障悬架各项性能指标均方根值对比结果如表2所示。）

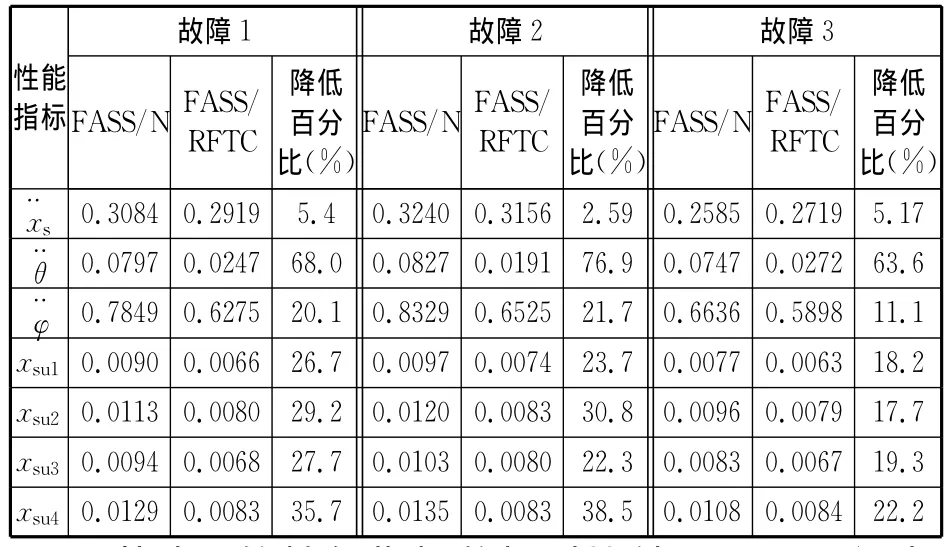
表2 FASS／N和FASS／RFTC的性能对比

从表2的性能指标数据对比结果可明显得出结论：最优鲁棒容错控制律控制下的故障悬架各项性能均优于正常H2／H∞状态反馈控制器控制下故障悬架性能，相对于后者，前者使悬架系统各项性能指标的均方根值均有明显降低。可见，最优鲁棒容错控制律对故障悬架控制相对正常H2／H∞状态反馈控制器控制具有较好的容错控制效果和一定的鲁棒性，进一步提高了汽车主动悬架控制可靠性。

5 结论

①事先考虑汽车主动悬架作动器故障和参数摄动情况，提出最优鲁棒容错控制律离线设计方法，运用多目标H2／H∞控制和有界实引定理将最优鲁棒容错控制律设计转化为LMI工具箱中最优可行解问题。②对于完好无故障汽车主动悬架，基于H2／H∞控制的最优鲁棒容错控制律对车辆乘坐舒适性控制效果接近于或优于正常H2／H∞状态反馈控制器控制下的效果。③对故障悬架采用最优鲁棒容错控制，车辆乘坐舒适性不但具有很好的控制效果，而且与在正常H2／H∞状态反馈控制器控制下的故障悬架相比较，最优鲁棒容错控制律控制下的故障悬架各项性能均优于前者，对汽车主动悬架参数摄动控制获得较强鲁棒性，对作动器故障控制获得很好的被动容错控制品质，提高了汽车主动悬架系统控制可靠性。

［1］ Yoshimura T，Teramura I.Active Suspension Control of a One－wheel Car Model Using Single Input Rule Modules Fuzzy Reasoning and a Disturbance Observer［J］.Journal of Zhejiang University Science，2005，6A（4）：251－256.

［2］ Campos J，Davis L，Lewis F L，et al.Active Suspension Control of Ground Vehicle Heave and Pitch Motions［C］／／Proceedings of the 7th Mediterranean Conference on Control and Automation.Haifa，Israel，1999，28－30.

［3］ Guia A，Melas M，Seatzu C，et al.Design of a Predictive Semi－active Suspension System［J］.Vehicle System Dynamics，2004，41（4）：277－300.

［4］ Zheng Ling，Li Yinong，Chen Bingkui.A New Semi－active Suspension Control Strategy through Mixed H2／H∞Robust Technique［J］.Journal of Central South University of Technology（Enlish Edition），2010，17（2）：332－339.

［5］ 张志勇，文桂林，钟志华.车辆主动悬架的混合H2／H∞最优保性能控制［J］.汽车工程，2007，29（7）：606－610.

［6］ Yetendje A，Seron M，De Dona J.Diagnosis and Actuator Fault Tolerant Control in Vehicle Active Suspension［C］／／Third International Conference on Information and Automation for Sustainability.Melbourne，2007：153－158.

［7］ Peter G，Zoltan S，Jozsef B.The Design of a Reconfigurable Suspension Control System Based on an FDI Filter［C］／／16th Mediterranean Conference on Control and Automation.Ajaccio，2008：446－450.

［8］ Crolla D，喻凡.车辆动力学及其控制［M］.北京：人民交通出版社，2003.

［9］ Ikenaga S，Lewis F L，Campos J，et al.Active Suspension Control of Ground Vehicle Based on a Full－vehicle Model［C］／／Proceedings of the American Control Conference.Chicago，2000：4019－4024.

［10］ Yu F，Crolla D A.An Optimal Self－tuning Controler for an Active Suspension［J］.Vehicle System Dynamics，1998，29（1）：51－65.

［11］ 俞立.鲁棒控制——线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002.

［12］ 陈明，童朝南.不确定系统鲁棒容错控制［J］.计算机仿真，2009，26（11）：186－190.

［13］ 陈无畏，孙启启，初长宝.汽车电动助力转向与主动悬架系统的H∞集成控制［J］.振动工程学报，2007，20（1）：45－51.

［14］ Guo Dingchen，Ma Yingyang，Li Yu.Mixed H2／H∞Optimal Guaranteed Cost Control of Uncertain Linear Systems［C］／／Proceedings of the Second International Conference on Machine Learning and Cybernetics.Xi’an，2003：784－788.

Optimal Robust Fault Tolerant Control for Vehicle Active Suspension System Based on H2／H∞Approach

Yang Liuqing1，2Chen Wuwei1Wang Hongbo1
1.Hefei University of Technology，Hefei，230009
2.Anhui Communications Vocational and Technical College，Hefei，230051

To improve control reliability and performance of a vehicle active suspension system，an optimal robust fault tolerant control method was put forward based on H2／H∞control for active suspension system with suspension parameter disturbance and actuator fault.The fault suspension models were built considering the ordinary actuator faults and parameter disturbance for suspension’s stiffness disturbance and damping coefficient disturbance.Based on the multi－objective H2／H∞statefeedback control approach and by bounded real cited theorem，the design condition of the optimal robust fault tolerant control for the suspension models was derived.By linear matrix inequality toolbox，an optimal robust fault tolerant controller under out－line state was designed for fault closed－loop system.Finally under the MATLAB／Simulink environment，the considerable simulations were carried out.The results show that proposed controller can improve the ride comfort performance of vehicle active suspension and of fault suspension too.Furthermore，control performance of the optimal robust fault tolerant controller is superior to the controller designed under the state of perfect suspension without faults.

vehicle active suspension；robust fault tolerant control；parameter disturbance；actuator fault

U461.4

10.3969／j.issn.1004－132X.2012.24.023

2012—07—18

国家自然科学基金资助项目（51075112）；安徽省高校省级自然科学研究项目（KJ2012B050）

（编辑 苏卫国）

杨柳青，男，1971年生。合肥工业大学机械与汽车工程学院博士研究生，安徽交通职业技术学院副教授。主要研究方向为车辆动力学及其控制、汽车检测技术、智能容错控制。陈无畏，男，1951年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。汪洪波，男，1981年生。合肥工业大学机械与汽车工程学院讲师、博士研究生。