我国人均国内生产总值的预测分析

余后强，李 玲

(咸宁学院a.数学与统计学院；b.生物医学工程学院,湖北 咸宁 437100)

0 引言

人均国内生产总值(人均GDP)的经济数据能较好的反映一个国家的经济这一复杂系统的宏观整体特征即动力学特征,但其经济数据在其主要的一些影响因素作用的同时常常还受到许多外生因素的影响，从而导致数据会产生突变，这就需要能够有较多的数据来研究其趋势和波动，并且希望在一定的趋势下，较少的数据就已经能体现出其趋势，大量的以往数据反而会影响对其数据的预测。那么该经济数据的预测模型如何建立就成为预测精度的关键所在【1】。

人均国内生产总值的时间序列为既含有确定性的动态趋势又含有随机性波动的非平稳时间序列,关于人均国内生产总值的一系列的模型的建立，时间序列分析法和灰色系统理论都可以做得到，并且时间序列分析法和灰色系统理论都各有各自的优点，时间序列分析法一般是建立在大量的历史数据的基础上进行模型的建立，进而对序列进行短期的预测。其预测方法的基本思想是：预测一个现象的未来变化时,用该现象的过去行为来预测未来。即通过时间序列的历史数据揭示现象随时间变化的规律,将这种规律延伸到未来,从而对该现象的未来作出预测【2】；而灰色系统理论则是一种动态趋势预测理论，它适用于在原始观测数据较少且数据已具有较为明显的趋势的预测问题，它能够较好地反映数据的趋势性变化【3】。

时间序列预测中的自回归移动平均模型（ARMA模型）是一种比较成熟的模型,因此可以通过对人均国内生产总值的时间序列的分析来研究我国经济发展的内在规律和演变机制[4][5]。灰色系统理论在控制、预测、决策等领域有着广泛的应用,但就其精华而言还在于GM(1,1)模型。GM(1,1)模型被广泛应用于预测,并且预测效果很好[6][7][8]。由于GM(1,1)算法简单易行,预测精度相对较高,所以在很多问题中,GM(1,1)模型仍是较好的预测模型。

本文将ARMA模型与GM(1,1)模型相结合用于人均国内生产总值的预测[9],首先采用ARMA模型方法在长期的数据的基础上研究其发展趋势，在已明确其发展趋势后利用最近的较少的数据建立GM(1,1)模型，进而继续对数据进行预测，这样既能延长被预测的序列，又能够避免某些突变的数据对预测序列的影响。实例表明，将以上两个模型结合起来构成的组合模型用于预测人均国内生产总值有较高的预测精度。

1 ARMA模型的建立

1.1 数据预处理

本文从国家统计局网站选取1978～2005年度的人均GDP（表1）作为我国经济发展的衡量标准。

为了验证模型的合理性，我们利用1978～1997年的20个数据进行模型的建立，1998～2005年的数据作为预测数据来验证。由表1可知我国的人均GDP的序列明显不平稳，对原序列先后进行对数化，一阶差分化后得到图1。

由图1可知此时的序列趋于平稳，然后对此序列进行零均值化，从而得到用来建模的序列。

图1 1978～1997年度的人均GDP

1.2 模型识别及参数估计

我们得到的平稳的零均值化的序列是一个ARMA(p,q）过程，则可用ARMA(p,q)模型来描述：

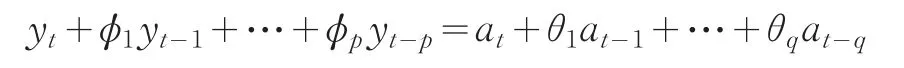
式中p和q分别是自回归部分和滑动平均部分的阶数；ϕi(i=1,2,…,p),θj(i=1,2,…,q)分别是自回归系数和滑动平均系数;at～N(0,σ2),t=1,2,…,n白噪声序列。故ARMA(p,q)模型有p+q+1个未知参数。要确定这些未知参数首先要确定模型的阶次,即p和q值。对于阶数(p,q)的确定是建模中比较重要的步骤，也是比较困难的步骤。一般地，我们可以运用基于自相关函数和偏相关函数的定阶方法、基于F检验、利用信息准则法确定阶数。这几种方法都各有各自的优缺点，往往可以把以上几种方法交叉结合运用。本文中，我们主要通过利用信息准则的方法中的最小信息准则(Akaike's Information Criterion,AIC)来定阶。其基本思想是根据模型的预报误差来判断自回归模型的阶数是否合适。如果某个适用的自回归模型是由某一序列拟合得来的,则利用该模型对序列进行一步预测,所得的预测误差必定是最小的。因此,预报效果的好坏,反过来也可作为模型拟合优劣的检验准则。

AIC函数为

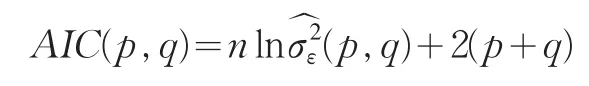
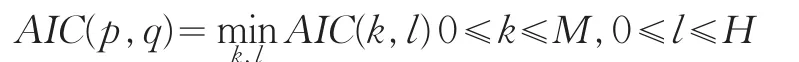
其中：M,N为ARMA模型阶数的上限值，一般取为

用该模型参数进行预测，然后转化到处理前最初的数据，详见表3。

表2 ARMA(1,3)模型参数

表3 预测数据与实验数据

由表3我们可以看出，用该模型预测出的数据与实际数据还是比较吻合的，具有一定的合理性。此时，得到的ARMA(1,3)模型为

1.3 模型检验

利用得到的ARMA(1,3)模型预测1998～2005年的数据，结果如表4所示:

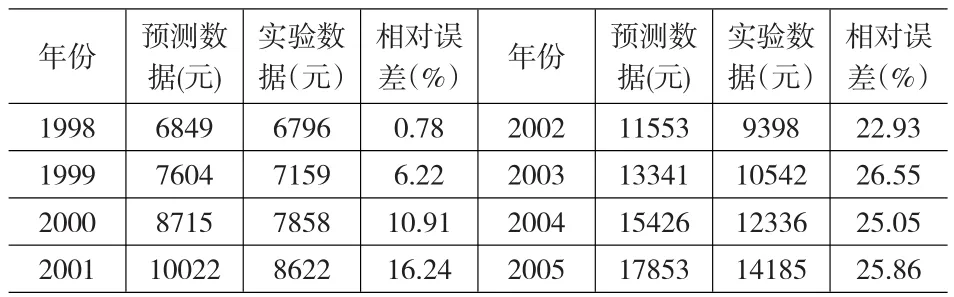
表4 预测数据与实验数据

由表4我们可知，随着预测序列的增加，准确性也随着降低。为了提高模型的精度，我们需要对模型进行改进。

2 ARMA-GM组合模型

2.1 GM模型建模原理

GM是一个拟微分方程的动态模型,它可以较好地描述系统内部特征和发展趋势,外推预测性能优于统计回归方程,且不要求样本数据有较大容量和满足一定统计分布。其建模过程为：

设原始非负数据序列为：

x(0)=[x(0)(1),x(0)(2),…x(0)(n)],其中

x(0)(i)＞0,i=1,2,...,n。

对原始非负数据序列作一次累加：

得出的x(1)=[x(1)(1),x(1)(2),…,x(1)(n)]为一次累加序列,根据灰色系统理论,对于一次列加生成序列

又令x(0)的GM(1,1)定义型为

则其一级参数包PΙ在最小二乘准则下有矩阵算式如下

则此微分方程的解即可得模型为

2.2 ARMA-GM组合模型应用

针对ARMA(p,q)模型预测稍长时误差过大的缺点，本文用GM(1,1)模型来对其进行改进，由于原序列的数据较为充分，这时我们就要确定数据的序列长度，我们如果确定的数据长度过短，经济数据的信息就不能够得到充分体现，并且预测的精度随着序列长度的增加也将明显下降；如果确定的数据长度过长，不但不方便计算，而且数据更有可能存在奇异数据，所以确定好数据的序列长度是十分重要的一步，在本文中选取序列的长度为6。

在确定了序列的长度以后，就需要确定这个GM模型长度为6的序列的数据，为了增加预测序列的精度以及序列的长度，我们需要在ARMA(p,q)模型的基础上用GM(1,1)模型来加以改进，在选取实验数据时，在建立GM(1,1)模型时如何确定序列的数据以提高预测的精度是改进的关键。在选取序列数据时原始数据和用ARMA(p,q)模型得到的理论数据的长度的选取就显得尤为重要，为此我们用不同的数据长度组合方式进行对比，截取的序列数据考虑到既需要有充足的ARMA(p,q)模型所预测的数据又需要有足够的对比数据，考虑到以上因素，我们选取1997～2002年的数据作为实验序列，经过比较，我们可知我们采用的ARMA(1,3)模型在预测两步内的精度较高，并且也能够很好地体现出经济数据的趋势。故此，我们采用4个原始数据与2个ARMA(1,3)模型预测出的数据结合的序列方式作为GM(1,1)模型建模的序列选取方式。

按此方式进行预测，我们得到模型的的参数a=-0.095682,b=4563.478922。则得到的模型为

x̂(1)(t)=51737.98e-0.095682t-47693.98 ，利 用 改 进 的ARMA-GM组合模型进行预测，另外为了对比我们直接用GM(1,1)模型进行预测得到的结果如表5所示。

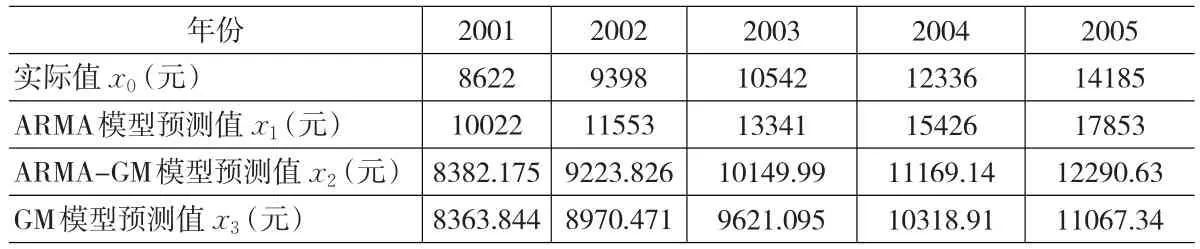
表5 各模型预测数据对比

2.3 模型评判

在评价对同一问题的不同模型的优劣时，我们可以用许多方法对其进行评价，在本文中我们采用灰关联度分析法[10]。

将实际值x0(k),k=1,…,5作为参考序列，ARMA模型预测值x1(k)、ARMA-GM模型预测值x2(k)以及GM模型预测值x3(k)作为比较序列。

根据表5求出差

显然

由此计算出关联系数如下：

令ρ=0.5，则有

从上述关联度分析来看，r02明显大于r01和r03，所以我们可知改进的模型明显优于原ARMA模型以及GM模型，ARMA-GM模型能够更精确地进行预测。

通过以上对改进模型的探讨，我们可知采用4个原始数据与2个ARMA(1,3)模型预测出的数据结合的序列方式的GM(1,1)模型比其它模型在该建模中有更好的优越性。

3 小结

ARMA模型在建模时能够在长期的数据的基础上研究其发展趋势，在进行短期预测时有很好的精确性，但是当预测稍长时预测的精度将明显的降低。采用本文提出的ARMA-GM组合模型能够很好的解决该问题，它不但能够在数据序列较少时比较准确地进行预测，而且随着预测序列的长度的增加精度降低的也较慢。

另外由于经济发展在不同历史阶段下发展规律有很大的差异等,并非建立的预测ARMA-GM组合模型中原始数据序列越长，采用的ARMA模型序列越长预测结果越好。

在本文中我们采用4个原始数据与2个ARMA(1,3)模型预测出的数据结合的序列方式作为GM(1,1)模型建模的序列选取方式。该改进的ARMA-GM组合模型与传统GM(1,1)模型以及ARMA模型相比,预测精度大大提高。因此,改进的GM(1,1)模型用于对其他经济方面的预测是可行的,效果比较理想。该方法具有一定的理论和实践意义。

[1]徐国祥.统计预测和决策[M].上海：上海财经大学出版社，2005.

[2]吴怀宇.时间序列分析与综合[M].武汉：武汉大学出版社，2004.

[3]肖新平,宋中民.灰技术基础及其应用[M].北京:科学出版社,2005.

[4]张恒茂，乔建国，史建红.国内生产总值的预测模型[J].山西师范大学学报（自然版），2008，（1）.

[5]赵婷.ARMA在我国GDP预测中的应用[J].中国市场，2011，（1）.

[6]李俊峰，戴文战.GM(1,1)改进模型的研究及在上海市发电量建模中的应用[J].系统工程理论与实践，2005，（3）.

[7]陈美英，杨金光.基于灰色GM(1,1)的邯郸市城镇化水平预测[J].湛江师范学院学报，2007，（3）.

[8]王道林.灰色预测模型GM(1,1)及其在山东省GDP预测中的应用[J].泰山学报学报，2008，28（6）.

[9]胡效雷，何祖威.基于GM-ARMA组合模型的年电力需求预测[J].广东电力，2007，（2）.

[10]马红燕.区域创新研发投入要素与GDP的关联度测算研究[J].统计与决策，2009，（16）.