假设检验功效的蒙特卡罗模拟

张建侠，鞠 银

（1.河南科技大学 数学与统计学院，河南 洛阳 471003;2.上海电机学院 数理教学部，上海 200240）

1 假设检验的两类错误

假设检验做出推断的基础是样本，是一种不完全归纳推断，尽管大多数情况下所作的推断是正确的，但也总有可能做出错误的决策。所犯错误有两类：一类是拒绝了实际上是成立的原假设H0，这类“弃真”的错误称为第I类错误，其概率大小用α表示，记为：第二类是接受实际上不成立的原假设H0，这类“存伪”的错误称为第II类错误，其概率大小用β表示，记为：

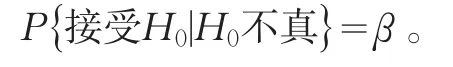
在确定检验法则时，我们应尽可能使犯两类错误的概率都较小。但是，一般来说，在样本容量固定时，若减少犯第一类错误的概率，则犯另一类错误的概率往往增大。若要使犯两类错误的概率都减小，除非增加样本容量。在给定样本容量的情况下，一般来说，我们总是控制犯第I类错误的概率，使它不大于α，α的大小视具体情况而定。这种只对第I类错误的概率加以控制，而不考虑犯第II类错误的概率的检验，称为显著性检验。在一些实际问题中，我们除了希望控制犯第I类错误的概率，往往还希望控制犯第II类错误的概率。

对有些统计量，比如样本均值，这两类错误可以通过分析的方法得到[5]。然而，如果假设检验方法的总体的正态性假设不能满足或者分析方法难以得到两类错误的表达式，此时通过蒙特卡罗模拟来估计第I类和第II类错误便是一个很好的选择。具体步骤如下。

算法1蒙特卡罗方法模拟计算第I类错误的步骤：

（1）确定在原假设成立条件下的总体服从的分布

（2）从总体中抽取样本容量为N的样本

（3）用临界值方法进行假设检验

（4）确定第一类错误是否发生，也就是看是否拒绝原假设；记录实验的结果

（5）执行第2步到第4步M次

在第6步中，实际上就是计算在M次试验中犯第I类错误的比例，以此作为给定临界值下检验显著性水平的估计值。

算法2下面给出蒙特卡罗方法模拟计算第II类错误的步骤：

（1）确定在原假设不成立条件下的总体服从的分布

（2）从总体中抽取样本容量为N的样本

（3）用显著性水平α和相应的临界值进行假设检验

（4）确定第二类错误是否发生，也就是看是否未拒绝原假设；记录实验的结果

（5）执行第2步到第4步M次

由此，犯第二类错误的概率可由M次试验中未拒绝原假设次数所占比率来估计。

值得注意的是，对假设检验中犯第II类错误的估计是通过对原假设不成立条件下分布的抽样得到的，因此会有许多犯第II类错误的可能，所以在分析第II类错误时必须指明选取的被择假设。

2 检验法的功效

众所周知，衡量检验模型优劣由其功效决定，所以计算功效函数极为重要。为此，首先引入施行特征函数的概念。

定义 若C是参数θ的某检验问题的一个检验法

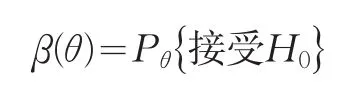
称为检验法C的施行特征函数或OC函数，其图形称为OC曲线。

由定义知，若此检验法的显著性水平为α，那么当真值θ∈H0时，β(θ)就是做出正确判断的（即H0为真时接受H0）的概率。故此时β(θ)≥1-α；而当θ∈H1时，则β(θ)就是犯第II类错误的概率，而 1-β(θ)是做出正确判断（即H0为不真时拒绝H0）的概率。函数1-β(θ)称为检验法C的功效函数。当θ*∈H1时，值1-β(θ*)称为检验法C在θ*的功效，它表示当参数θ的真值为θ*时，检验法C做出正确判断的概率。

由功效函数定义可以看出，求功效函数就是求第I类和第I类错误；而两类错误我们可以用蒙特卡罗方法模拟得到。

3 数值算例

假设检验的形式有左边检验、右边检验和双边检验三种，对应的功效函数也有三种不同的情形。在此仅以下面“产品质量抽验方案”问题为例做出对功效函数的模拟，其他形式假设检验可类似由蒙特卡罗模拟得到。

解：检验问题可表示为：

H0:μ≤μ0，H1:μ＞μ0

且要求当μ≥μ0+δ=140时能以1-β=0.95的概率拒绝H0。

在此例的假设下，给出功效函数的蒙特卡罗模拟，结果如图1，图2。

从模拟结果可以得到以下结论：

(1)由图1μ≤120时的图像可知，实际上α=0.05是犯第一类错误的最大可能，这一最大值仅当真实μ为原假设定义的μ0=120时达到。

(2)图1也显示功效函数取值与样本容量有关，在其他检验条件保持不变，仅增加样本容量，两种错误类型的概率α和β同时减少。

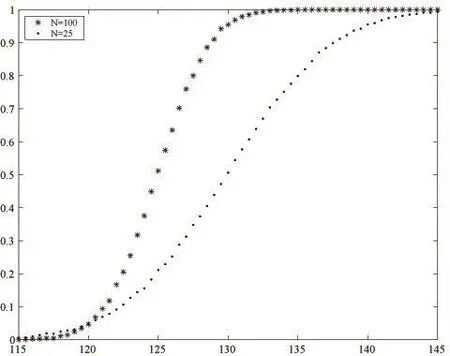
图1 μ取不同值时的检验功效

图2 μ=140时检验功效与样本容量

(3)从图1可以看到参数的真值μ(μ＞μ0)在μ0附近时，检验法的功效很低。这表明，即便样本容量N很大，要想对所有的μ∈H1控制犯第二类错误的概率都很小是不可能的。

(4)图2得到不同样本容量下μ=140时的检验功效值，可见在N=24或N=25时，功效函数取值已满足例题的要求，这与分析方法得到的N≥24.35符合的非常好。

几点说明：

①在以上模拟中，模拟次数均为M=10000；②限于篇幅，在此处没有单独给出假设检验两类错误α,β的模拟结果及其与样本容量N和模拟次数M的关系；③在此处仅以右边检验为例给出了功效函数的蒙特卡罗模拟，但此处的模拟方法也适用于其他检验形式；在构造的检验统计量分布函数未知的检验中，蒙特卡罗模拟方法仍然适用，此时还需要用模拟方法产生构造的统计量的分位数以确定拒绝域。

本文给出了假设检验中两类错误的蒙特卡罗模拟，不仅可以作为某些分析方法得到的两类错误的实验验证；对分析方法难以得到显示表达的两类错误，也可直接模拟得到其近似值。检验功效是评价检验法检验效果的重要指标，在统计分析中有重要应用。本文以产品质量抽验方案为例给出了功效函数的蒙特卡罗模拟结果，本模拟方法也适用于无法得到功效函数显示表达式的更复杂情况。总之，本题介绍功效函数的蒙特卡罗模拟可用于假设检验中样本容量的确定，不同的检验法检验效果比较等统计分析问题。

[1]高惠璇.统计计算[M].北京：北京大学出版社，2006,(1).

[2]盛骤，谢式千，潘承毅.概率论与数理统计[M].北京：高等教育出版社，2005,(3).

[3]高洪，孙平辉.假设检验中检验效能的研究进展[J].中国热带医学，2007，7(2).