基于智能PI的永磁同步电动机近似最大转矩电流比控制

张伦健，陈利萍

(中国矿业大学，江苏徐州221008)

0引 言

由于永磁同步电动机具有体积小、功率密度高、效率和功率因数高等优点，其调速系统越来越多地应用于各种工业场合。目前永磁同步电机电流矢量控制方法有id=0控制、UPF控制、恒磁链控制、最大转矩电流比(以下简称MTPA)控制、弱磁控制及最大输出功率控制等，针对一类永磁同步电动机d、q轴电感不等特性，MTPA控制在相同电流下可输出更大的转矩，因而在系统容量相同的情况下相对id=0控制可显著提高系统动态性能［1］。但MTPA控制时的转矩电流关系非线性，实际应用中难以实时对方程进行求解。文献［4］通过离线计算出电磁转矩对应d、q轴电流关系，再用查表的方法查得转矩对应电流，这样可提高运算速度，但会占用大量存储资源。本文在永磁同步电动机数学模型及MTPA控制理论基础上，通过优化算法研究了一种适用于工程的近似MTPA控制，并将智能PI调节器引入所研究系统。文中对传统PI与智能PI调节下的MTPA及近似MTPA控制进行比较，仿真结果验证近似MTPA控制的正确性与可行性，同时智能PI控制下的系统的动态性能优越。

1永磁同步电动机数学模型及MTPA控制

1．1永磁同步电动机数学模型

将d轴定向于永磁同步电机转子磁链方向，可得dq轴系下PMSM电压、磁链、转矩与运动平衡方程。定子电压方程:

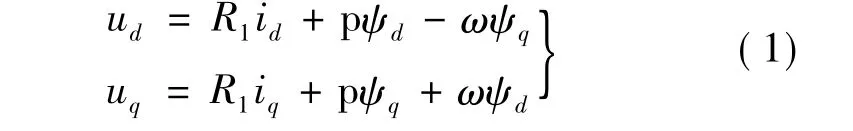
定子磁链方程:

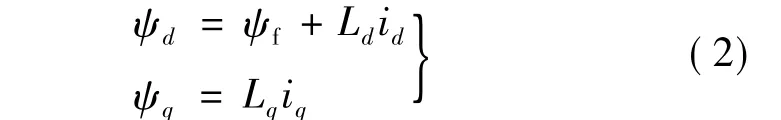
电磁转矩方程:

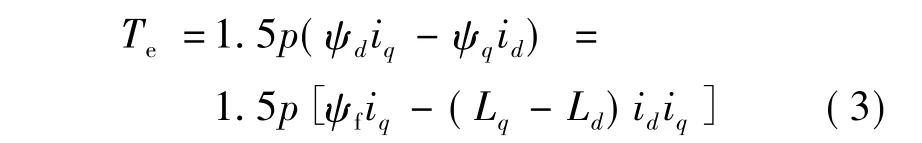
运动平衡方程:

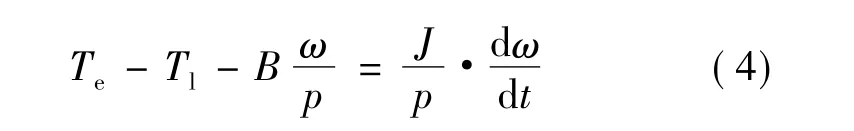
式中:ud、uq为 d、q 轴电压;id、iq为 d、q 轴电流;R1为定子相电阻;Ld、Lq为dq轴电枢电感;ψf为转子磁链;ψd、ψq为 d、q轴磁链;p为电机极对数;ω 为转子旋转电角速度;p为微分算子;Te为电磁转矩;B为阻力系数;J为转动惯量［2-3］。

1．2永磁同步电动机MTPA控制

永磁同步电动机id=0控制是将定子电流矢量定向于q轴，使得Is=iq，电磁转矩中的磁阻转矩分量被控制为零，因此在相同的定子电流下id=0控制时的转矩非最大［1，4］。为使磁阻转矩为驱动转矩，可控制定子电流矢量超前q轴以实现MTPA控制，MTPA控制系统原理图如图1所示。

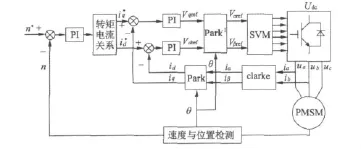
图1 永磁同步电动机MTPA控制原理图

永磁同步电动机定子电流幅值:

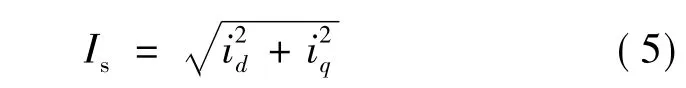
为了实现MTPA控制，系统等效为求满足式(5)的转矩极大值问题［3］。作拉格朗日函数L:

式中:λ为拉格朗日算子。

将式(6)分别对id、iq及λ求偏导数并令其为零，得到:

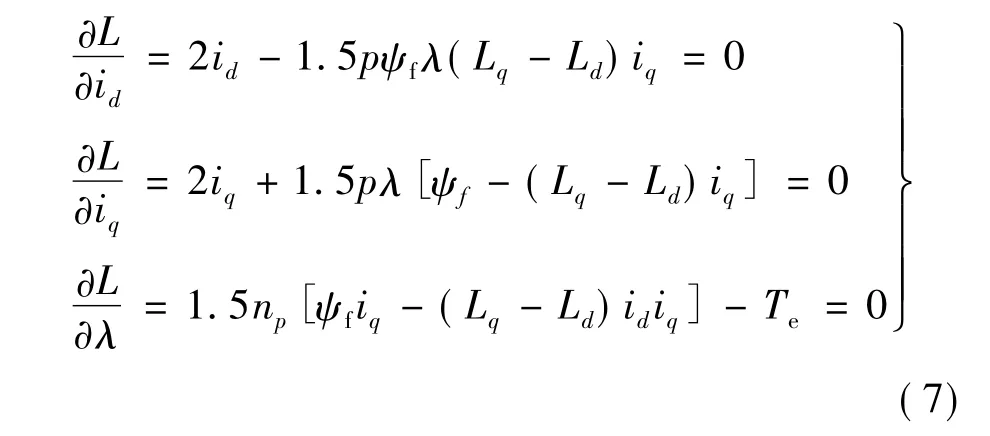
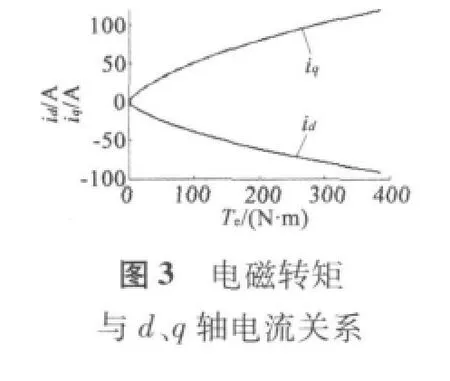
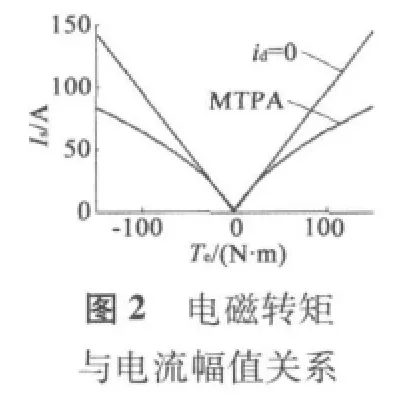
通过求解式(7)可以得出转矩与d、q轴电流之间及其与电磁转矩的关系［3］，式中数据详见表1。系统在id=0与MTPA控制下电磁转矩与电流矢量幅值关系如图2所示，MTPA控制下的电磁转矩与d、q轴电流关系如图3所示。

2永磁同步电动机近似MTPA控制

实际应用永磁同步电动机MTPA控制可采用离线计算电磁转矩与电流的对应关系，系统实时查表运行，但该方法会占用大量存储单元［4］。为了更适用于工程实际，本文研究了一种近似MTPA控制，通过算法优化将d、q轴电流id、iq与电磁转矩关系线性化［1］。

设采用MTPA控制时id、iq与电磁转矩的关系:

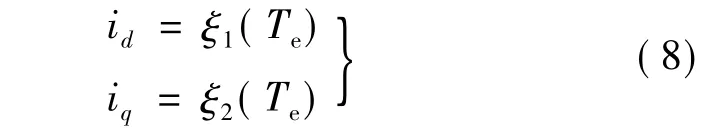
将式(8)代入式(3)可得:

由于 ξ1(η)与 ξ2(η)均非线性，为便于计算，采用近似线性函数表示，令:

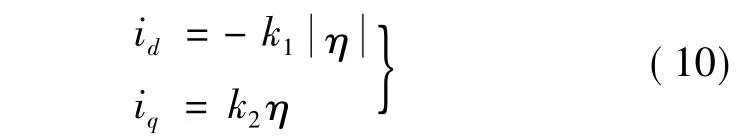
式中:η为转速调节器输出。将式(10)代入式(3)得:

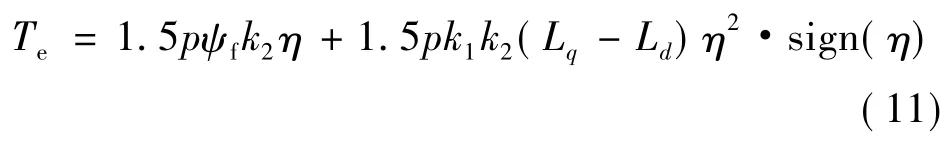
电机的定子电流幅值:

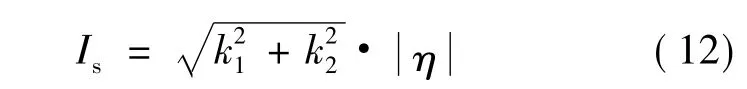
定子电流的幅值正比于速度调节器的输出，但电磁转矩与定子电流为非线性关系。为求得定子电流下的最大转矩，需选择合适的k1、k2。令

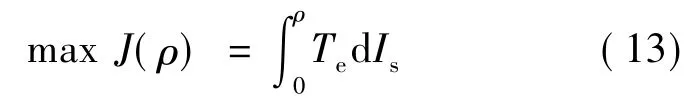
由式(11)和式(12)，若 Te＞0，则:

由式(13)、式(14)可得:

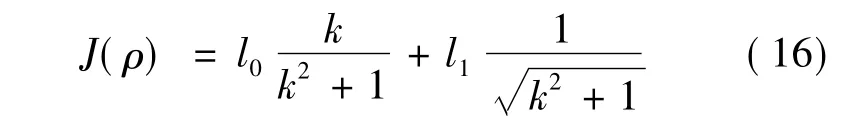
为使J(ρ)最大，将J(ρ)对k进行求偏导，并令偏导数为零，得:

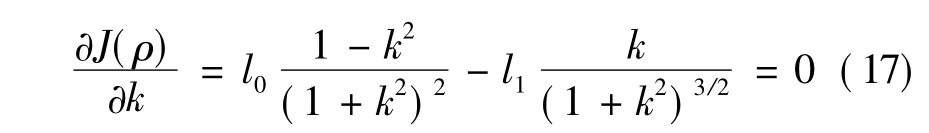
对上式进行化简并令:

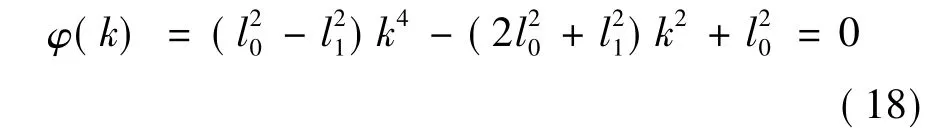
由Newton-Raphson迭代原理，k的迭代解:

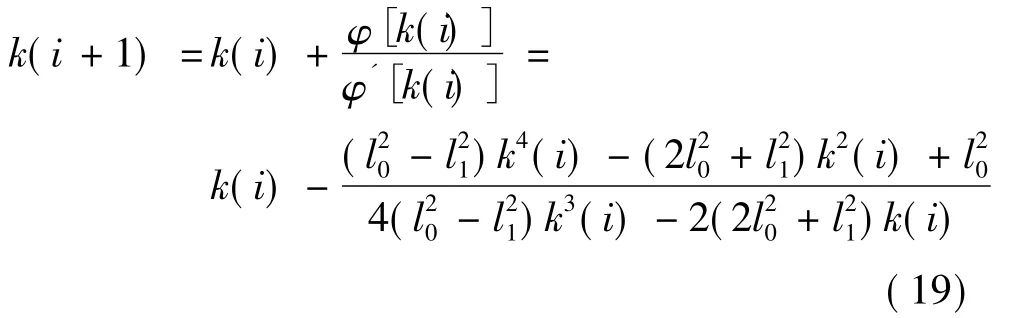
当 ρ=15 A、Ld=4．5 mH、Lq=8．5 mH、ψf=0．175 Wb、p=4 时，利用迭代式(19)解得 k==0．213 4，由可解得 k1=0．208 7，k2=0．978 0。图4为id=0、MTPA及近似MTPA控制时的转矩电流关系。由图可知，近似MTPA与MTPA控制时的转矩电流关系曲线几乎重合，说明两者的控制效果非常接近。

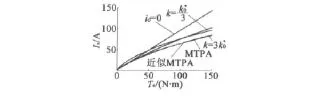
图4 不同情况下的转矩电流关系

3智能PI调节器

3．1智能PI调节器原理

传统PI调节器的参数确定后不再改变，难以适应系统的部分复杂工作状态［6］。偏差、偏差的积分以及偏差的微分分别表示系统的现在、过去及将来的三种状态，若合理地利用以上三种信息，则可构成一种动态改变结构及参数的智能PI调节器以快速消除偏差，减小或消除超调，使系统的动态性能得以提升［2，5］。

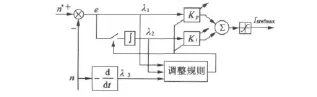
图5 智能PI调节器结构图

3．2参数调整规则

智能PI调节器根据偏差的大小进行参数实时调整，有以下两种情形:

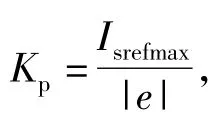
(2)当偏差范围较小(|e|≤ξ)时，需及时调整Kp、Ki，以避免过调，令 Kp≥0，Ki≥0。小范围偏差时的调整规则可分为以下三种情况［5-7］。

(a) 当 λ1λ3＜0(λ1＞0、λ3＜0或 λ1＜0、λ3＞0)时，偏差趋于零，需减小比例部分(Kp)的作用，且Kp的衰减速度与偏差接近于零的速度成正比。其中λ1＞0、λ2＞0时积分作用可产生加速转矩，减小偏差;λ1＜0、λ2＜0时积分作用可产生制动转矩，同样减小偏差。反之，λ1＞0、λ2＜0时积分作用可产生制动转矩，增加偏差;λ1＜0、λ2＞0时积分作用可产生加速转矩，同样增大偏差。综上，λ1λ2＞0时需增大 Ki，λ1λ2＜0时需减小 Ki。可得调整规则:

式中:np1与ni分别为比例系数Kp及积分系数Ki的调整速率。

(b) 当 λ1λ3＞0(λ1＞0、λ3＞0 或 λ1＜0、λ3＜0)时，偏差|e|增大，Kp需以较快的速度增大，使λ3与λ1同号，偏差|e|越大，Kp增大越快，Ki的调整规则与λ1λ3＜0相同。可得调整规则:

式中:np2为比例系数Kp的调整速率。

(c) 当 λ1λ3=0，即 λ1=0 或 λ3=0 时，采用保持Kp、Ki不变的方式。

4系统仿真

基于MATLAB建立仿真模型，电机主要技术数据设置如表1所示。分别对传统PI与智能PI调节下MTPA控制及近似MTPA控制进行仿真分析。系统起动负载转矩为7 N·m，0．15 s负载转矩突增到14 N·m，给定转速n*=700 r/min。系统仿真波形如图6～图8所示。

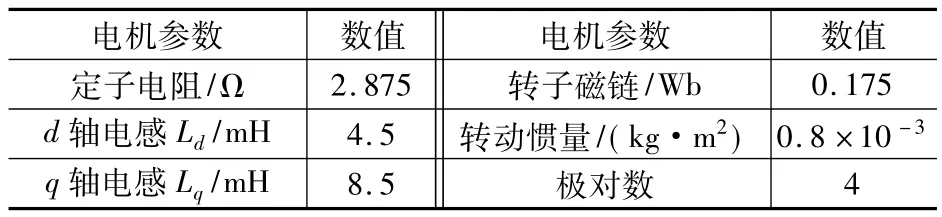
表1 PMSM主要技术数据

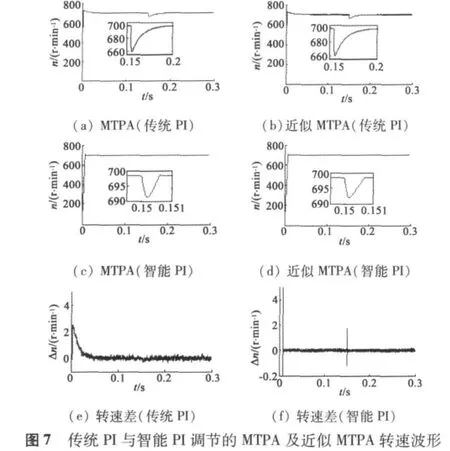
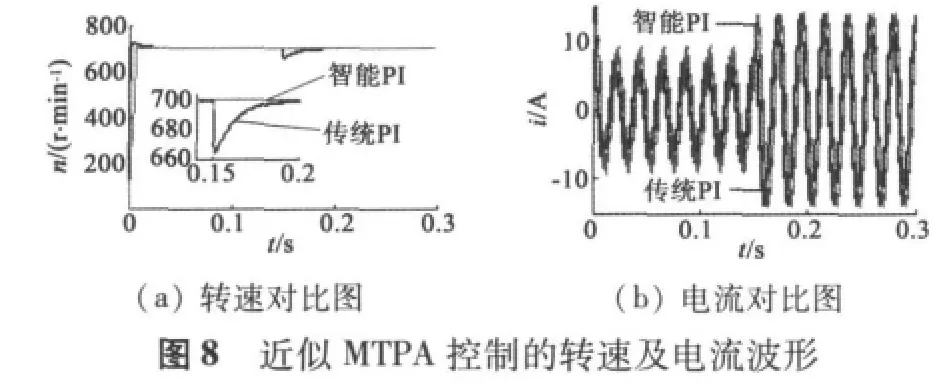
图6为传统PI调节的转矩电流比及电流对比图。由图6(a)可知，负载突增时id=0控制下的转矩电流比值不变，即转矩电流呈线性关系，而MTPA控制下的转矩电流比值随着负载转矩的增大而上升，转矩电流呈非线性关系，且负载转矩越大，转矩电流比相对id=0控制亦越大，MTPA控制下的定子电流幅值略小于id=0控制时的定子电流。由图6(b)可知，MTPA与近似MTPA控制的转矩电流比及电流对比波形非常接近，说明近似MTPA控制在工程上可取代MTPA控制。

图7为传统PI与智能PI调节下MTPA及近似MTPA转速波形。由图7(a)、图7(b)，传统PI调节下两者转速响应曲线大致相同，转速差波形如图7(e)所示，但在0．15 s负载转矩载突增时系统动态性能较差，存在约为40 r/min的明显速降，且恢复时间较长，约为0．05 s;由图7(c)、图7(d)，智能PI调节下两者的转速响应曲线同样大致相同，转速差波形如图7(f)所示，负载突增时系统的动态性能较传统PI调节有较大改善，通过局部放大图可见，速降降低至约8 r/min，恢复时间约减小到0．000 8 s，整体波形看不出明显的速降;图7(e)、图7(f)所示的MTPA与近似MTPA控制时转速差波形显示，传统PI控制下转速差需要0．05 s归零，而智能PI控制下转速差只需要约0．01 s即可归零。

图8的近似MTPA控制在传统PI及智能PI调节下的转速及电流对比波形表明，智能PI调节时系统动态性能明显优于传统PI调节下的动态性能，两者的定子电流响应基本相同。

5结 语

本文在永磁同步电动机MTPA控制的基础上将非线性的转矩电流关系进行线性化，研究可应用于工程实际的近似MTPA控制，系统性能与MTPA控制时相似度高，在定子电流幅值有限的情况下提高了电机的电磁转矩。将智能PI调节器应用于近似MTPA控制，改善了系统性能，具有较高的应用价值。

［1］ 李长红，陈明俊，吴小役．PMSM调速系统中最大转矩电流比控制方法的研究［J］．中国电机工程学报，2005，25(21):169-174．

［2］ Tursini M，Parasiliti F，Zhang Daqing．Real-time gain tuning of PI controllers for high-performance PMSM drives［J］．IEEE Transactions on Industry aplications，2002，38(4):1018-1026．

［3］ 郎宝华，刘卫国，贺虎成，等．基于最大转矩电流比动态磁链给定的直接转矩控制［J］．电气传动，2008，38(1):23-26．

［4］ 李长红，陈明俊，吴小役．基于DSP的永磁同步电动机控制系统的研究［J］．电气传动，2005，35(4):7-10．

［5］ 阮毅，徐静，陈伯时．智能PI控制在交流调速系统中的应用［J］．电工技术学报，2005，20(3):80-84．

［6］ 陈伯时．电力拖动自动控制系统［M］．北京:机械工业出版社，2006．

［7］ 郭卫杰，刘维亭，林永才．智能PI算法在永磁同步电动机控制系统中的应用［J］．微特电机，2011，38(3):34-37．