超磁致伸缩材料动态磁滞特性理论分析
2012-07-23何忠波孙华刚李冬伟李玉龙
崔 旭,何忠波,孙华刚,李冬伟,李玉龙
(军械工程学院,河北石家庄050003)
0引 言
超磁致伸缩材料(以下简称GMM)是一种新型功能材料,具有高响应速度、宽工作频域、大输出应变等优异特性,以其为核心的超磁致伸缩致动器广泛应用于微位移控制、精密加工、流体控制等领域[1]。但GMM随着频率增大非线性磁滞特性显著增强,这种非线性特性主要造成了两方面的影响:首先GMM输出应变随着频率变化而变化,对GMM器件控制系统提出了较高的要求;其次GMM的能量耗散随着频率的增大而增强,耗散的能量令GMM温度升高从而影响输出能力[2]。所以对GMM动态磁滞特性进行研究是超磁致伸缩器件设计、总体性能的预测及控制策略设计的重要前提。本文将对GMM棒的磁滞特性进行理论分析。
Jiles、Atherton等提出了一种基于畴壁理论的磁化强度磁滞模型,并先后推导了静态J-A模型和动态J-A模型[3]。该系列模型可以较好地描述铁磁材料所受磁场强度H与材料磁化强度M的关系。郑晓静等提出的Z-L模型能较好描述磁化强度M和磁致伸缩应变λ间关系[4]。交变磁场下,磁场强度从GMM棒表面到中心逐渐衰减,这种现象称为趋肤效应,该效应使得GMM棒内实际磁场强度磁小于励磁线圈提供的磁场强度。孙华刚等计算了不同频率交变磁场下GMM棒内平均磁场强度,并引用静态J-A模型对GMM动态特性做出了预测[5]。以上成果对GMM输出特性预测方面有较好的指导作用,但均无法很好地描述GMM动态能耗特性。
本文在考虑GMM内部分布的基础上结合动态J-A模型,建立了GMM棒的动态磁滞模型,可以较好地描述在动态磁场作用下GMM棒内部磁场分布情况、涡流损耗以及异常损耗,从而可以较好地预测GMM棒磁滞非线性的变化规律以及能量损耗特性。
1考虑内部磁场分布的数学模型
动态驱动下,GMM棒中磁场沿径向分布并不均匀。根据麦克斯韦方程,GMM棒中磁场分布的柱坐标系方程[5]:
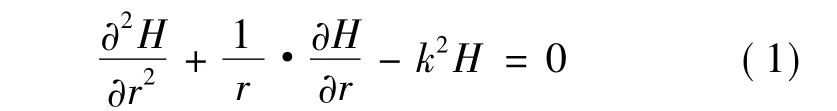
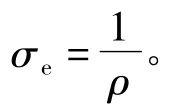
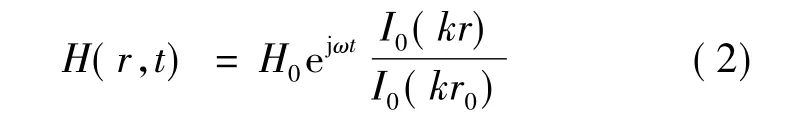
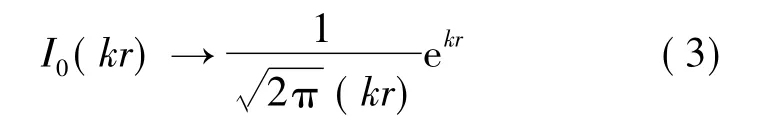
从而有:
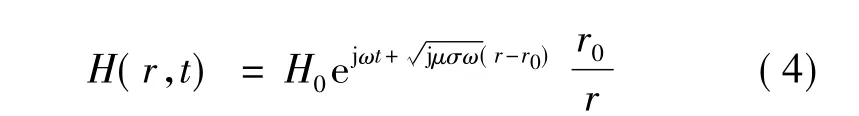
由式(4)可知,GMM棒中磁场强度径向分布不均,GMM棒径向截面平均磁场强度可表示:
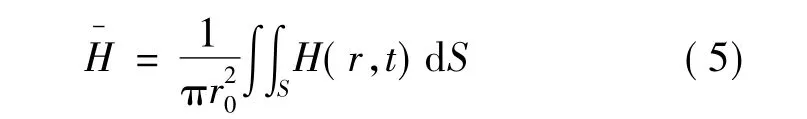
Jiles、Atherton 等建立的动态 J-A 模型为[7]:

Z-L模型可以描述GMM棒在预压应力下的总应变ε与磁化强度M的关系[4]:

对式(1)~式(9)中定参数取值[8-10],如表1所示。

表1 模型中的参数取值
2动态磁滞特性分析
分析式(9),频率参数f或ω不会影响磁化强度M和磁致伸缩应变ε的关系,所以首先着重讨论不同频率下磁场强度H与磁化强度M的关系。考虑材料内部的磁场强度分布状况时,需先利用式(5)计算材料内部平均磁场强度,然后将平均磁场强度代入式(6)求解。
为了验证求解结果对GMM棒动态磁滞特性的描述能力,本文将文献[8]中的动态实验结果与求解结果进行对比。如图1所示,相同的磁场强度情况下,实测的GMM磁化强度最大值随着驱动频率的增加而减少,而磁化强度的最大值变小使得GMM输出应变变小;滞环宽度随着频率的增加而增加,滞环宽度和长度的变化使得滞环面积发生变化,最终导致了GMM磁滞非线性的增强以及能量耗散的增大[8]。对式(5)和式(6)代入与实验相同的磁场:偏置磁场为16 kA/m,励磁磁场为 H=8sin(2πft)kA/m,励磁频率分别为 f=10 Hz、100 Hz、500 Hz。
图1(a)是驱动频率为10 Hz时,实验滞回环与计算滞回环的最大值相同,但计算滞回环稍宽;图1(b)是驱动频率为100 Hz时,实验滞回环与计算滞回环最大值基本一致,且滞环宽度基本一致;图1(c)是驱动频率为500 Hz时,实验滞回环与计算滞回环最大值相近,且滞环宽度基本一致;以上三组对比中,理论计算的磁化强度最大值误差为8%(图1(c)),滞环宽度最大值误差11%(图1(b)),滞环面积误差11%(图1(a)),表明理论计算与实验结果吻合度较高。
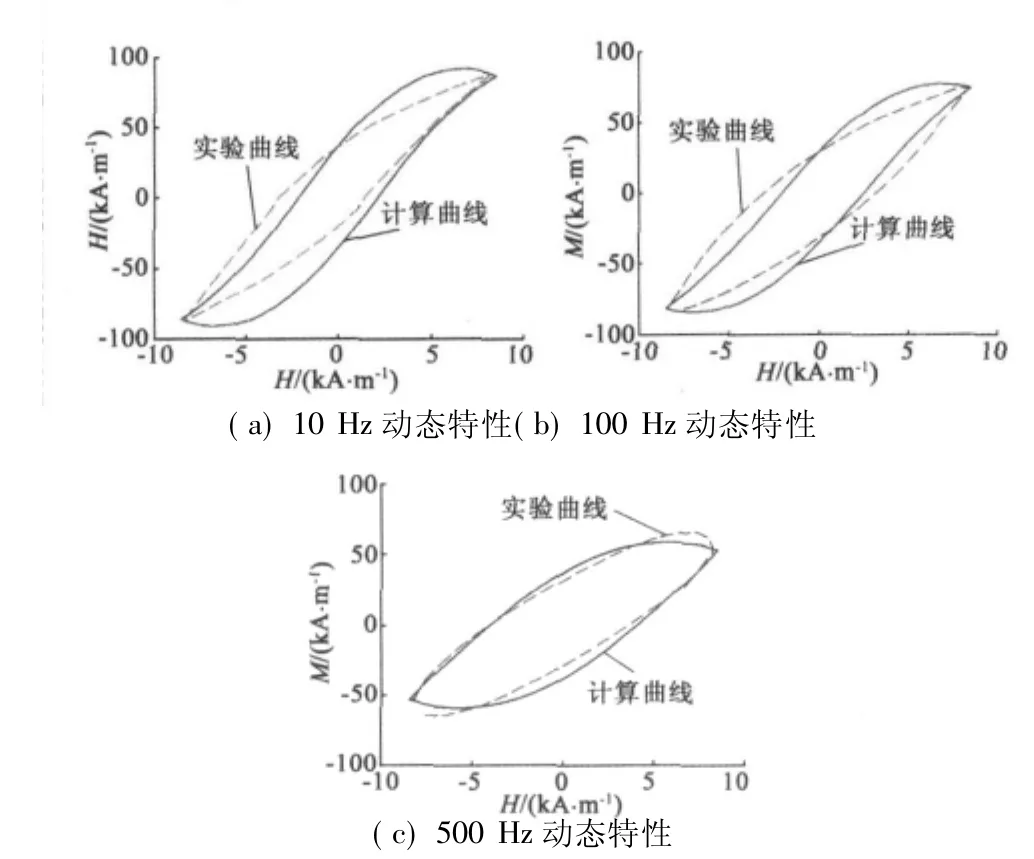
图1 计算结果与文献[8]实验数据对比
3动态磁滞特性预测
上文已经证明了结合式(5)和式(6)能够较好地描述动态磁滞特性,可以利用其对超磁致伸缩棒的动态特性做出预测。
仅对式(6)进行求解,求解结果可以反映不考虑GMM棒内磁场分布的前提下磁场强度和磁化强度的关系。当磁场H=100sin(2πft)kA/m,频率为f=50 Hz、100 Hz、500 Hz时得到如图 2 的 H-M 滞回曲线,可见不考虑材料内部磁场分布的前提下,不同频率滞环的最大值相同,该结论与实验有较大的差距。
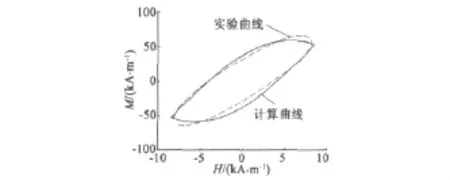
图2 不同频率下H-M滞回特性
当考虑材料内部磁强分布状况时,需先利用公式(5)计算材料内部平均磁场强度,然后将平均磁场强度代入式(6)求解。励磁磁场H=100sin(2πft)kA/m,且频率分别为 50 Hz、100 Hz、500 Hz下的 H-M修正滞回曲线如图3所示。比较图2和图3,图形产生了一定的变化,可知高频驱动下应考虑GMM内部磁场强度分布状况。分析图7中不同频率的滞回环特征,随着频率的增大,主要发生了两方面的变化:第一,高频滞回环最大值变小,这是由于高频驱动下GMM棒内部磁场分布不均匀造成的,500 Hz时GMM内部平均磁场强度为励磁磁场强度的69%;第二,高频滞回环逐渐加宽,这是由于高频驱动下涡流损耗和异常损耗造成的[4]。对比图2和图3,考虑GMM内部磁场分布情况时500 Hz时HM滞回线面积为50 Hz时的1.9倍,而不考虑内部磁场分布情况时却高达3.6倍,两者差距较大。

图3 考虑材料内部磁场分布时H-M滞回环
磁滞非线性造成了GMM的非线性动态输出特性,联立式(5),式(6)和式(9)即可预测GMM棒动态输出特性。值得注意的是,公式(5)计算结果为GMM棒内部平均磁场强度,然后联立式(6)和式(9)得到的磁致伸缩应变λ是指GMM棒的平均应变。在无偏置磁场条件下,励磁磁场为H=40×sin(2πft)kA/m,且频率分别为 1 Hz、100 Hz、500 Hz下GMM棒的H-λ滞回曲线如图4所示:相同励磁磁场下,随着励磁频率的增加,GMM棒的应变逐渐减小,500 Hz时的输出能力为1 Hz时的73%。
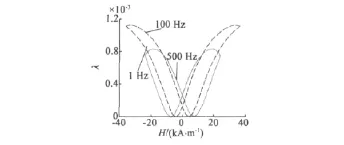
图4 GMM棒输出特性预测
以上预测对GMM器件的设计和控制工作具有重要的指导意义:(1)GMM器件设计时应充分考虑GMM棒输出应变随频率增大而减小的现象,高频驱动下的器件能够适当增大励磁磁场来弥补GMM棒输出应变的减小。(2)H-M滞回环的面积即为每周期驱动下GMM棒能量损耗的大小,通过其可预测器件中GMM棒发热情况,以对GMM器件的温度控制系统设计进行指导。(3)根据不同频率下HM滞回环的形状设计对应的逆模型,以对GMM器件进行补偿控制。
4结 论
(1)在考虑GMM棒内部磁场分布的前提下,结合动态J-A模型建立了GMM动态磁滞模型。
(2)通过与文献实验数据对比,验证了动态磁滞模型可以较好地描述GMM棒的动态磁滞特性。
(3)计算结果表明,随着频率的增加,GMM棒内部磁场强度分布、涡流损耗和异常损耗因素对磁滞特性影响更加明显,故高频驱动下,此三者均不能忽略。
(4)随着频率的增大,H-M滞回环以及H-λ滞回环均发生了两方面变化:GMM内部磁场随着频率增大而减小,导致了滞回环最大值逐渐变小;涡流损耗和异常损耗随着频率增大而增大,导致了滞回环逐渐加宽。
[1] Urai T,Tanaka H.Development of a Giant Magnetostrictive Actuator and the Application to a Servovalve[J].Transactions of the Japan Hydraulics and Pneumatics Society,2001,32(3):53 ~57.
[2] Jiles D C,Atherton D L.Ferromagnetic hysteresis[J].IEEE Trans.on Magn.,1983,19(5):2183-2185.
[3] Jiles D C.Modeling the Effects of Eddy Current Losses on Frequency Dependent Hysteresis in Electrially Conducting Media[J].IEEE Trans.on Magn.,1994,30(6):4326-4328.
[4] 孙乐.超磁致伸缩材料的本构理论研究[D].兰州:兰州大学,2007.
[5] 孙华刚,袁惠群.超磁致伸缩材料内部磁场与涡流损耗理论分析[J].东北大学学报(自然科学版),2008,29(3):371-374.
[6] 袁惠群,孙华刚.超磁致伸缩材料滞回非线性特性分析[J].兵工学报,2009,30(2):180-184.
[7] Jiles D C.Challenges in incorporating nonlinear hysteretic behaviour into modelling of magnetic materials[R].USA Iowa:The Institution of Engineering and Technology Electromagnetic Professional Network,2006.
[8] Calkins F T.Design,analysis and modeling of giant magnetostrictive transducers[D].USA:Iowa State University,1997.
[9] Dapino M J.Nonlinear and hysteretic magneto-mechanical model for magnetostrictive transducers[D].USA:Iowa State University,1999.
[10] Chen Y H,Jiles D C.The magnetomechanical effect under torsional stress in a cobalt ferrite composite[J].IEEE Trans.on Magn,2001,37(4):3069-3071.?
