具有AR（1）误差的线性回归模型的统计诊断

凌 佳，言方荣

（1.江苏广播电视大学，南京 210036；2.中国药科大学 数学教研室，南京 210009）

0 引言

线性回归模型在许多实际问题中得到了广泛应用，通常随机误差项都假设是正态白噪声且具有方差齐性，但在一些复杂问题中会显得不太合适。当观测值与时间有关时，数据之间往往存在序列相关，尤其是自相关性。因此，这时对模型不仅要进行异方差检验，还要进行相关性的检验。对于具有AR（1）误差的线性模型，Tsai（1986）得到了同时检验异方差和相关性的Score统计量。

对于具有方差齐性的均值漂移模型和数据删除模型，文献[1]给出了相应的估计量、诊断统计量以及二者的等价性证明。对于异方差的条件下的均值漂移模型，文献[2]得到了有关的估计量。本文进一步推广和发展了他们的结果，首先讨论具有AR（1）误差的均值漂移模型，得到了均值扰动值的Score检验统计量，接下来再讨论具有AR（1）误差的数据删除模型，证明了该模型与具有AR（1）误差的均值漂移模型之间并不具有等价性。最后，通过boq数据来说明了分析方法的合理性和有效性。

1 具有AR（1）误差的均值漂移模型

其中Y=(y1,…yn)T为n维观察向量，X=(x1,…xn)T为n×p阶列满秩矩阵，di表示一个n维向量，其第i个分量为 1，其他均为零；β=(β0,β1,…,βp-1)T为p维未知参数，γ为扰动值。ε为n维随机误差向量，参数φ满足而{at}为一白噪声序列，为未知参数。

记参数θ=(γ,βT,φ,σ2)T，θ0=(0,β,φ,σ2)T。参数θ与θ0的极大似然估计（MLE）分别记为：

考虑如下假设检验问题：

显然，若H0成立，则认为(yi,xiT)不是异常点；若H0被否定，则认为(yi,xiT)为异常点。

引进a=(at)n×1，ε=(εt)n×1。n阶矩阵：

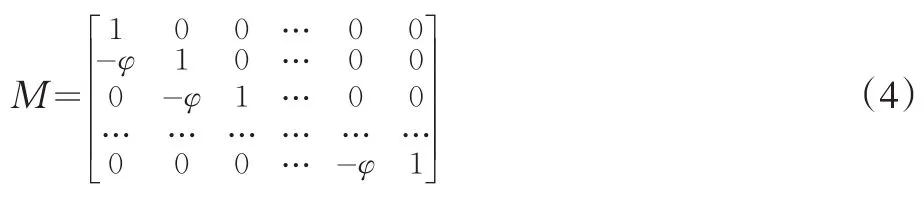
则a～N(0,σ2In)

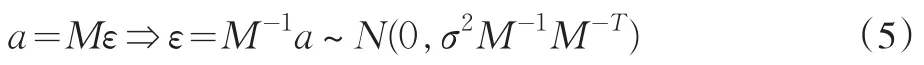
其中M-T=(M-1)T。从而具有AR（1）误差的均值漂移模型中参数θ的对数似然函数为：

定理1 对于模型（1）、（2），假设检验问题（3）的Score检验统计量为：

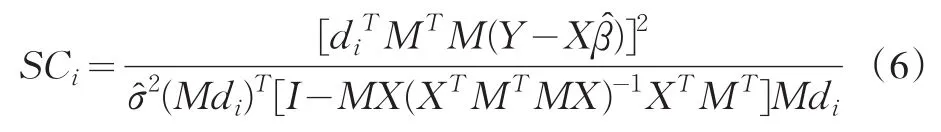
其中M在θ̂0处计值。

证明：可求出l(θ)关于θ的前二阶导数如下：

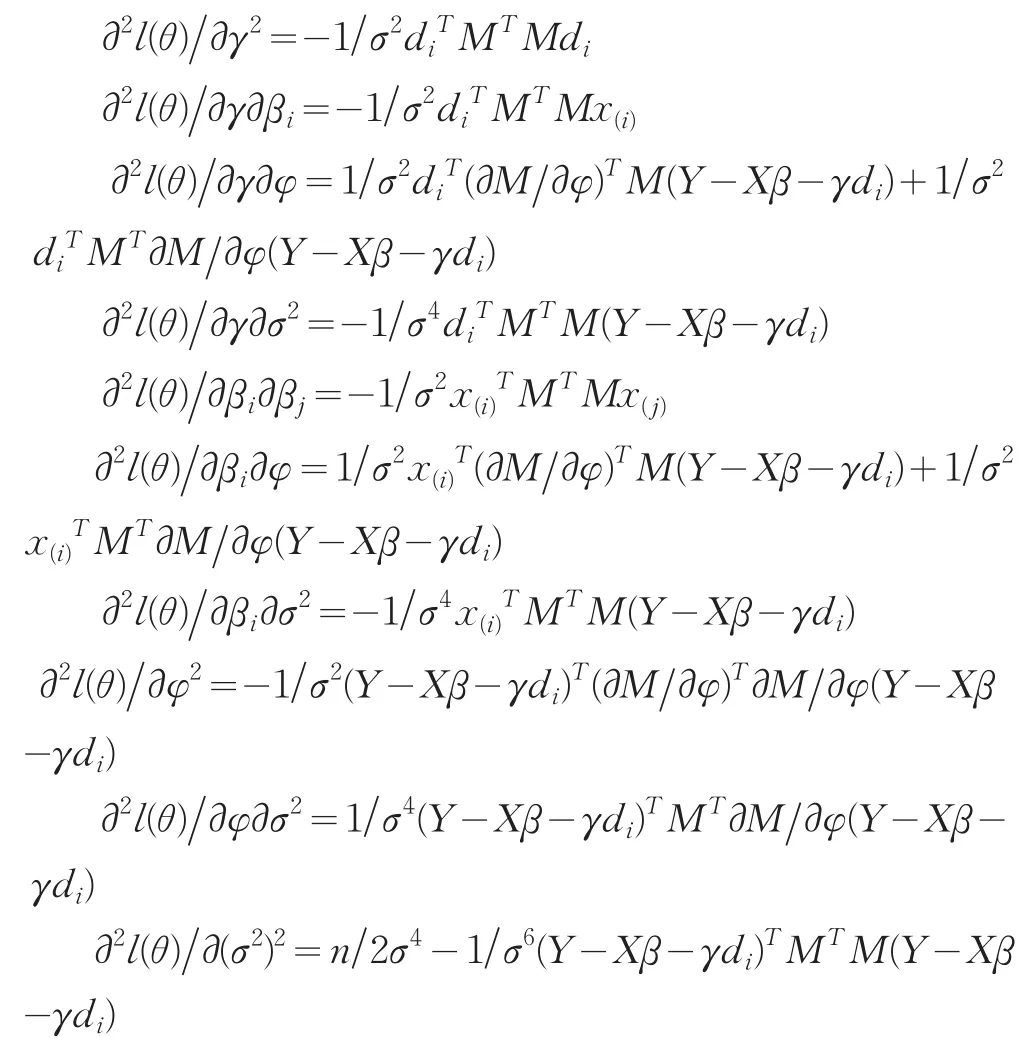
由此可得：

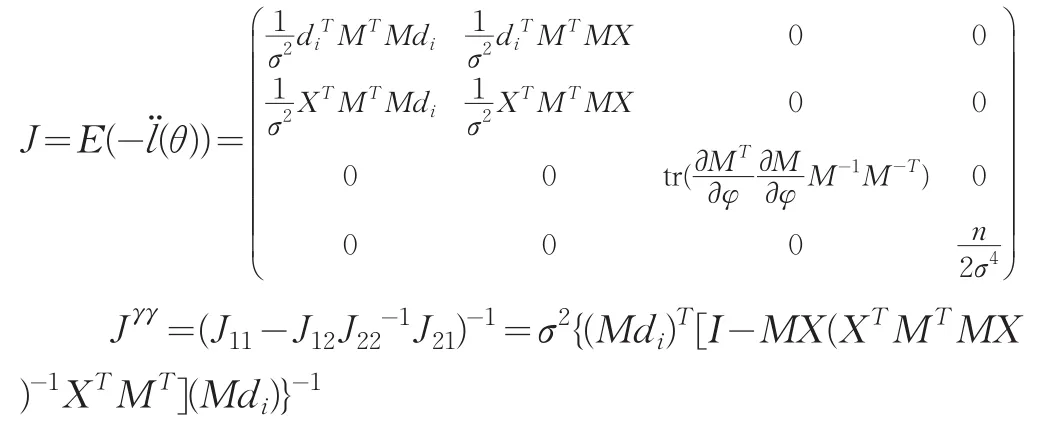
从而：

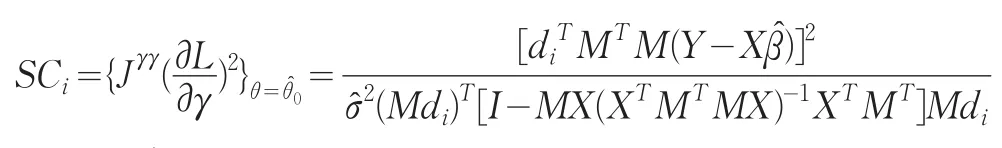
证毕.

H0成立时，β，φ，σ2的极大似然估计（MLE）分别为:

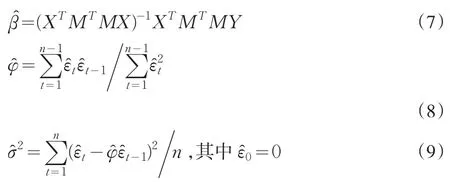
推论1若φ=0，则表示方差无自相关，由（6）式可得

（10）式的SCi实际上就是方差齐性时均值漂移模型的均值扰动值的Score检验统计量，这与已知结果吻合。

2 具有AR（1）误差的数据删除模型

其中Y(i)、X(i)、ε(i)分别为1中的Y、X、ε去掉第i行而得到的；β=(β0,β1,…,βp-1)T为p维未知参数。σ2为未知参数。

引进a(i)=(a1,…,ai-1,ai+2,…,an)T(n-2)×1，ε(i)=(ε1,…,εi-1,εi+1,…,εn)T(n-1)×1。矩阵：

M(i)为M去掉第i行，第i+1行，第i列而得到的。则：

下面研究具有AR（1）误差的均值漂移模型和数据删除模型相应的估计量是否相同，即二者是否具有等价性。首先：对于具有AR（1）误差的均值漂移模型

由Y=Xβ+γdi+ε，两边同乘以M得到一个新的模型：

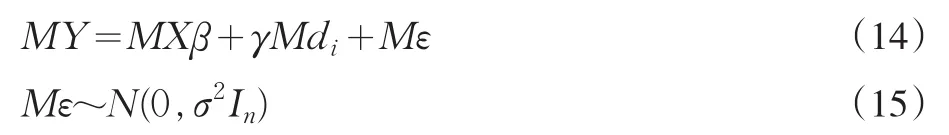
求该模型中的参数β的LSE就转化为求模型（14）、（15）中的参数β的LSE。

由[1]中的单参数附加变量的参数估计公式可得β的LSE为：

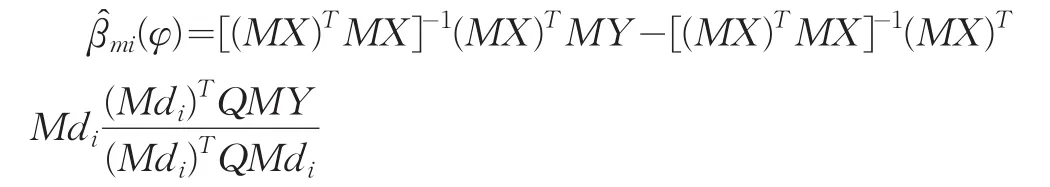
其中Q=I-PMX=I-MX[(MX)TMX]-1(MX)T

其次：对于具有AR（1）误差的数据删除模型

由Y(i)=X(i)β+ε(i)，两边同乘以M(i)得到一个新的模型：

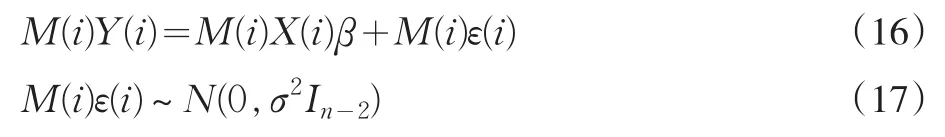
求具有AR（1）误差的数据删除模型中的参数β的LSE就转化为求以上模型中的参数β的LSE。

由[1]中的参数估计公式可得β的LSE为：

矩阵A由n阶单位阵去掉第i行和第（i+1）行而得到，矩阵B由n阶单位阵去掉第i列而得到。

此时，M(i)=AMB，X(i)=BTX，代入上式经过化简整理可得：

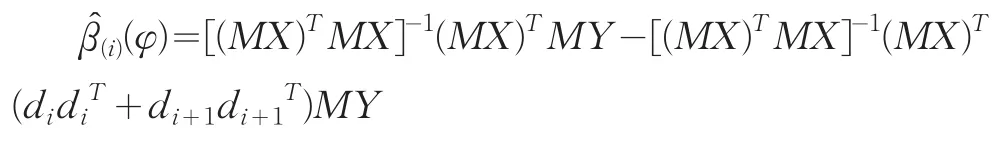
不等式的意义在于得到了在AR（1）误差的条件下，均值漂移模型和数据删除模型二者不是等价的。

这与文献[5]中具有异方差的均值漂移模型和数据删除模型二者是等价的结果是不同的。

3 实例分析

由[1]知boq数据的方差齐性不太好，如果用通常的线性回归模型（误差项服从标准正态分布），则有好几个点拟合的效果都不够理想，同时考虑到误差项之间可能存在自相关。此时进行异常点的诊断可运用模型(1)。

利用（3）式计算假设检验（2）的Score值如表1：

表1 Score检验统计量的值

由表1知SC11=6.5189＞χ2(1)=3.841，所以第11号点可能有漂移。事实上，由下面的散点图可以发现第11号点确实有漂移，与计算结果吻合。

4 结语

由于具有AR（1）误差的均值漂移模型和数据删除模型二者不是等价的，因此在讨论具有AR（1）误差的线性回归模型的异常点时，不能像讨论具有异方差的线性回归模型那样仅仅考虑更便于处理的均值漂移模型。用定理1的Score检验统计量进行异常点的诊断，经过实例分析发现用该方法进行异常点诊断的效果是比较好的。

图1 方差扰动时的散点图

[1]韦博成，鲁国斌，史建清.统计诊断引论[M].南京：东南大学出版社，1991．

[2]宗序平，韦博成.线性回归诊断的若干问题[J].高校应用数学学报，1993，（3）．

[3]Sanford Weisberg.Applied LinearRegression[M].Chichester:John Wiley&Sons,1985．

[4]R.Dennis Cook,Sanford Weisberg.Diagnostics for Heteroscedasticity in Regression[J].Biometrika,1983，l70（1）.

[5]凌佳，夏乐天.具有异方差的线性回归模型的统计诊断[J].河海大学学报，2008，（2）．