滚动轴承声发射特征的单分类方法及其应用

2012-07-21胥永刚冯明时谢志聪张建宇

轴承 2012年9期

胥永刚，冯明时，谢志聪，张建宇

(北京工业大学北京市先进制造技术重点实验室, 北京 100124)

滚动轴承是各种旋转机械中应用最广泛、最易损坏的零件之一，其工作状态直接影响整个系统的精度、性能、寿命及可靠性等[1]。目前滚动轴承故障诊断最常用的方法是振动检测，由于声发射检测技术能弥补振动方法的诸多不足，例如能更早发现表面缺陷的产生、不易受到周围低频环境噪声的影响[2]，因此将声发射检测技术应用于滚动轴承的状态检测和故障诊断具有重要意义。

分类决策是故障诊断系统的重要组成部分，基于人工神经网络以及基于支持向量机的模式识别等多分类方法被应用于故障诊断中，但该类方法均需要事先获取各种故障模式下的若干组数据样本。在机械设备故障诊断中，正常运行状态的数据样本容易获得，而故障样本一般难以获得，极端情况下甚至没有故障样本。对此类问题，支持向量数据描述(Support Vector Data Description,SVDD)方法提供了较好的解决方案[3-4]。SVDD是一种单分类方法，只需要一类样本即可进行分类，且具有计算速度快、能有效利用小样本数据等特点。

由于声发射信号的采样频率很高，数据量很大，不适于直接作为分类的特征向量，而谐波小波包由于小波基在频域的盒形特性，可将信号分解到相互独立互不重叠的若干频带内。鉴于此，将谐波小波包分解和支持向量数据描述相结合，以对滚动轴承的声发射特征进行单分类智能诊断。

1 谐波小波

小波包分解可以将信号分解到不同的频带，信号在各频带的能量反映其特征。由于谐波小波具有严格的盒形频谱特征，使用谐波小波包可以将信号准确地分解到各个不同的频带，且不会出现重叠或遗漏，因此使用谐波小波包进行分解提取各个频带的能量作为特征向量能比其他小波得到更好的效果。

1.1 数学模型

广义谐波小波在频域的定义式为

(1)

对(1)式进行Fourier反变换可得广义谐波小波的时域表达式

ψm,n(t)=(ej2nπt-ej2mπt)/[j2(n-m)πt]，

(2)

此处用m,n来标识频带为[2mπ,2nπ]的不同尺度小波，从而形成一系列频带相邻的小波集。在水平m,n下对广义谐波小波做k/(n-m)(k∈Z)的平移，由(2)式可得

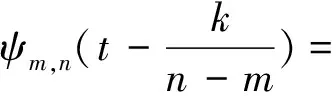
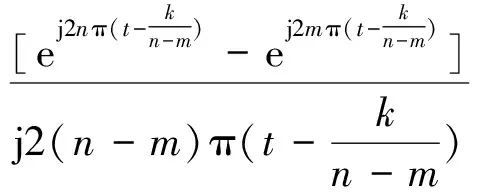
(3)

(3)式即为分析带宽为(n-m)2π，分析时间中心在t=k/(n-m)处的谐波小波的一般形式[5]。时间离散信号x(n)的谐波小波变换的计算过程如图1所示[6]。

1.2 谐波小波包分析

与其他小波包分析类似，谐波小波包分解的子频带数必须是2的s次幂，s(s∈Z+)代表分解层数，于是信号被分解成2s个子频带，每个子频带带宽fb为

fb=fh/2s，

(4)

式中：fh为信号的最高分析频率。

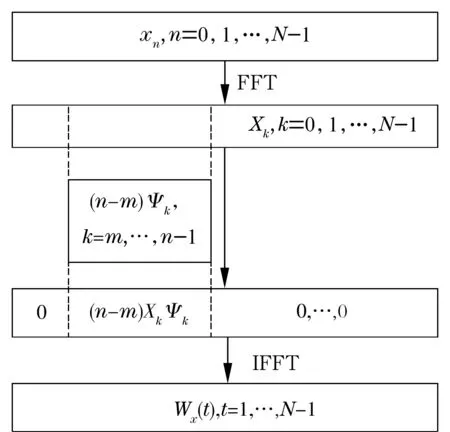
图1 时间离散信号x(n)谐波小波变换的计算过程

由于谐波小波的带宽是(n-m)2π，m,n应满足

2π(n-m)=2πfb，

(5)

进而可以确定

m=i×fb,n=(i+1)×fb;i=0,1,…,2s-1。

(6)

这样，谐波小波包分析的系数可以由谐波小波变换求得WPx(s,i,k)=Wx(m,n,k)。

1.3 能量特征提取

当轴承运行状态发生变化时，其不同频带内的声发射信号能量将发生变化，即各频带能量分布与轴承缺陷或故障相关。因此可以先利用谐波小波包将信号分解到相互独立的若干个子频带，然后提取各频带内的能量信息作为轴承工作状态的重要特征和有效指标，以实现对轴承工作状态的监测和诊断。对原始信号序列{x(n),n=0,1,…,N-1}，利用谐波小波包分解后重构得到的信号为{x(i,l),i=1,…,2s;l=0,1,…,N-1}，定义第i频带的能量占原始信号总能量的相对能量为[7]

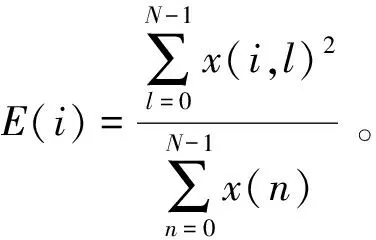
(7)

2 支持向量数据描述

支持向量数据描述算法的基本思想是将要描述的对象作为一个整体，建立起一个封闭而紧凑的区域，即寻找一个最小体积的超球体，使得被描述对象尽可能多的包容在该超球体内。支持向量数据描述仅需要目标样本即可产生单分类器，但当存在少量的非目标样本时，这些非目标样本可以被用于提高分类的准确性。

假定有N个要描述的数据xk(k=1,2,…,N)，即构建单值分类器的学习样本，其中有s个目标样本数据表示为xi(i=1,…,s)，剩余的为非目标样本表示为xm(m=s+1,…,N)。

该方法目标是要寻找到一个最小体积的超球体，使所有的xi都包含在该球体内，同时所有的xm都在该球体之外。该超球体可用其中心α和半径R来表示。这样的超球体应满足

min(f)=R2，

(8)

约束条件:‖xi-α‖2≤R2(i=1,2,…,s)；‖xm-α‖2≥R2(m=s+1,…,N) 。为增强其分类的鲁棒性，引入松弛因子ζi≥0,ζm≥0，(8)式变为

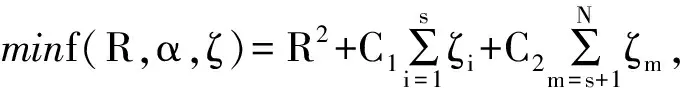
(9)

约束条件: ‖xi-α‖2≤R2+ζi，‖xm-α‖2≥R2-ζm。其中C1，C2为指定的常数，起到控制错分样本惩罚程度的作用，以实现在错分样本的比例和算法复杂程度之间的折中。上述问题可以转化为Lagrange极值问题，即

(10)

式中：α，γ≥0,均为Lagrange系数。对于每一个xk，都有一个对应的α和γ，经过变换，上述Lagrange优化目标函数可写为

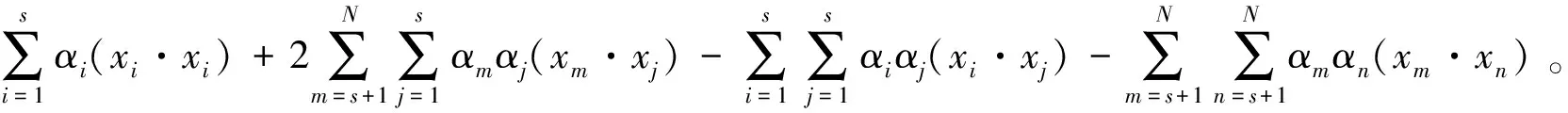
(11)

引入下标k,l(k=1,…,N;l=1,…,N)来表示新变量α′=yα(其中y=1表示目标类，y=-1表示非目标类)，(11)式可以改写为

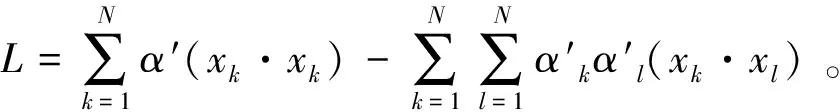
(12)

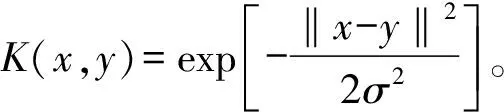
(13)

测试样本z到超球体中心的距离

(14)

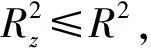
3 基于谐波小波包分解的SVDD故障诊断方法

利用上述谐波小波分析方法提取轴承声发射信号各频带的能量比例作为特征向量，然后将这些特征向量输入到SVDD分类器，利用SVDD进行模式识别，具体方法如下：

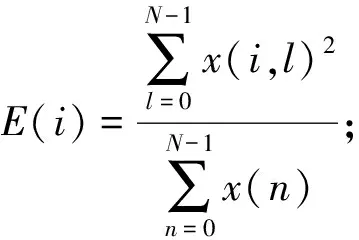
(2)以步骤(1)求得的相对能量构造目标样本的特征向量

T=[E(1),E(2),…，E(i),…];

(3)利用步骤(2)中构造的特征向量作为训练样本，训练SVDD分类器；

(4)使用步骤(1)，(2)中的方法提取待检测信号的能量特征向量，将其输入到步骤(3)训练的SVDD分类器中，根据分类结果就可以得知信号对应的轴承状态(目标样本对应正常轴承信号，非目标样本对应故障轴承信号)。

4 试验研究

4.1 试验方案

滚动轴承试验台如图2所示。三相异步电动机通过带传动带动转轴旋转，利用该试验台模拟滚动轴承的工作状态，在试验台上安装2套N205滚动轴承，轴承座3处安装正常轴承，轴承座4处安装模拟故障轴承。测试中电动机转速为940 r/min。

1—三相异步电动机；2—传动带；3，4—轴承座

通过对轴承内、外圈线切割加工模拟裂纹故障，裂纹缺陷宽度为1 mm；对滚动体做腐蚀加工模拟点蚀故障，点蚀缺陷为直径0.5 mm，深0.1 mm的小凹坑。声发射采集系统包括SR150M声发射传感器、PAI前置放大器、声发射检测仪以及计算机。将涂上耦合剂的声发射传感器固定在轴承座4上，利用声发射采集仪和计算机采集声发射数据，设置采样频率为800 kHz，采样点数为26144。采集轴承正常、外圈裂纹、内圈裂纹、滚动体点蚀4种模式下的声发射信号，每种模式采集50组信号。

4.2 特征提取

由于轴承故障与声发射信号的频率分布情况相关，利用谐波小波包将信号分解为5层包括32个子频带，并按1.3节提出的能量特征提取的方法求各子频带所占的能量比例。由于后16个频带包含的能量非常小，因此，只做出正常轴承信号与3种故障轴承信号的前16个频带所占能量比例的柱形图做比较。如图3所示，在前8个能量频带，正常轴承与故障轴承有较大区别。因此选取前8个频带(对应0～12.5 kHz到87.5～100 kHz)的能量比例作为支持向量数据描述分类器的特征向量。

4.3 试验结果

SVM模式识别方法是近年来较多应用于故障诊断领域的分类方法[7]，为了说明SVDD单分类器相对多分类器的优点，将SVDD与SVM的分类效果进行对比。

对正常样本进行特征提取后，在其中任意抽取20组作为正常训练样本，剩余30组作为测试样本。同样抽取外圈裂纹、内圈裂纹各2组作为故障训练样本，在剩余各类样本中分别任意抽取30组作为测试样本。虽然滚动体点蚀的样本并没有作为训练样本，但仍然从其中抽取30组作为测试样本以测试分类器对于未知故障的分类情况。

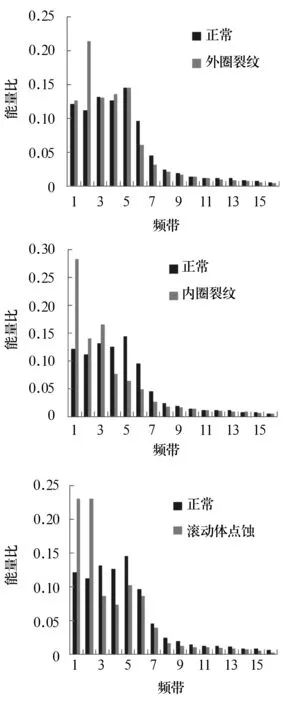
图3 正常轴承与故障轴承的能量比对比

以正常训练样本作为目标向量，故障训练样本作为非目标向量输入SVDD进行训练。在构建SVDD分类器时，拒绝率设为0.05，参数σ设为1，使用的核函数为Gauss核函数。

将正常训练样本、故障训练样本分别作为两类向量输入SVM分类器。采用最小二乘算法，分类模式为一对多。

生成SVDD与SVM分类器后，分别将测试向量输入两个分类器测试以比较其识别能力，结果见表1(测试样本均为30组)。

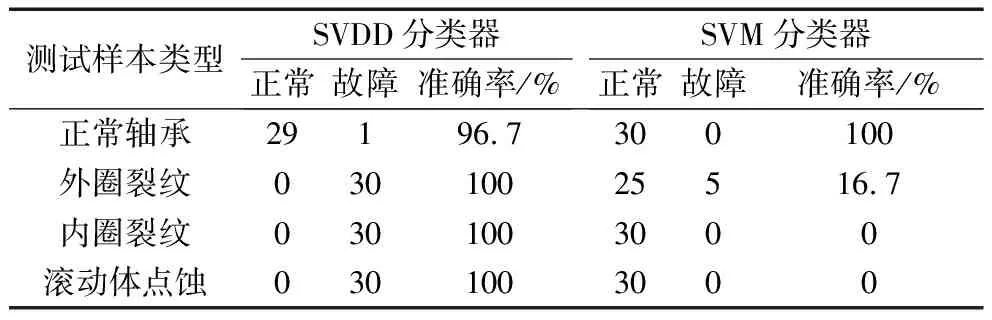
表1 SVDD与SVM识别效果对比

从表1中可以看出，两种方法都能很好地识别正常样本，但是SVM分类器将大多数故障样本错误地识别成了正常样本，其原因是：训练时正常类与故障类数据量差别很大，导致SVM分类器的超平面向故障类方向推移。而SVDD分类器很好地解决了数据不对称带来的问题，无论在故障还是正常样本的识别中都取得了良好效果。而且对于训练时并未使用的滚动体点蚀样本，依然可以正确识别。表1说明在正常样本与故障样本数量差距较大的情况下，与SVM相比，SVDD能取得较好效果。