强噪声背景下的滚动轴承故障微弱信号检测新方法
2012-07-20王晶陈果郝腾飞
王晶,陈果,郝腾飞
(南京航空航天大学 民航学院,南京 210016)
滚动轴承故障诊断是旋转机械状态检测与故障诊断的重要内容,滚动轴承出现早期损伤性故障的一个特点是微弱的周期信号宽带冲击会激起系统结构自身的高频振动,其频谱图中会出现多个共振带。传统的共振解调技术[1]应用相当广泛,然而如何有效确定共振带位置并提取共振调制边频带是该方法的不足之处。小波变换[2]具有带通滤波特性,可以选择合适的小波和分解层数,对信号进行分解和重构,自动提出共振频带,因此目前得到了广泛应用。然而,滚动轴承信号的信噪比低,尤其是早期故障,故障信号的能量很小,非常微弱,信号经常淹没在噪声中,即使应用小波分析得到了小波包络谱,其仍然存在谐波众多,故障特征不够凸显的问题。文献[3]提出了时延相关解调法对滚动轴承故障信号进行降噪处理,得到了较好的效果,为了更加凸显故障信号,使降噪效果更好,在现有方法的基础上,提出了一种滚动轴承故障微弱信号检测的新方法,该方法使用AR模型和多重自相关分析法有效降噪,并使用小波包络分析,凸显了滚动轴承的故障特征。
1 故障信号检测方法介绍
1.1 方法流程
滚动轴承故障检测新方法的检测流程如图1所示,其使用AR模型和多重自相关结合的方法对信号进行降噪处理。该方法与时延相关解调相比的优点是可以进行多次降噪,不需要先了解信号和噪声的特性,最大范围地凸显故障频率;与传统小波分析相比的优点是对信号进行了预处理。新方法的适用性更强,在强噪声背景下,可以对信号进行多次的降噪处理,提取出滚动轴承故障的特征频率。
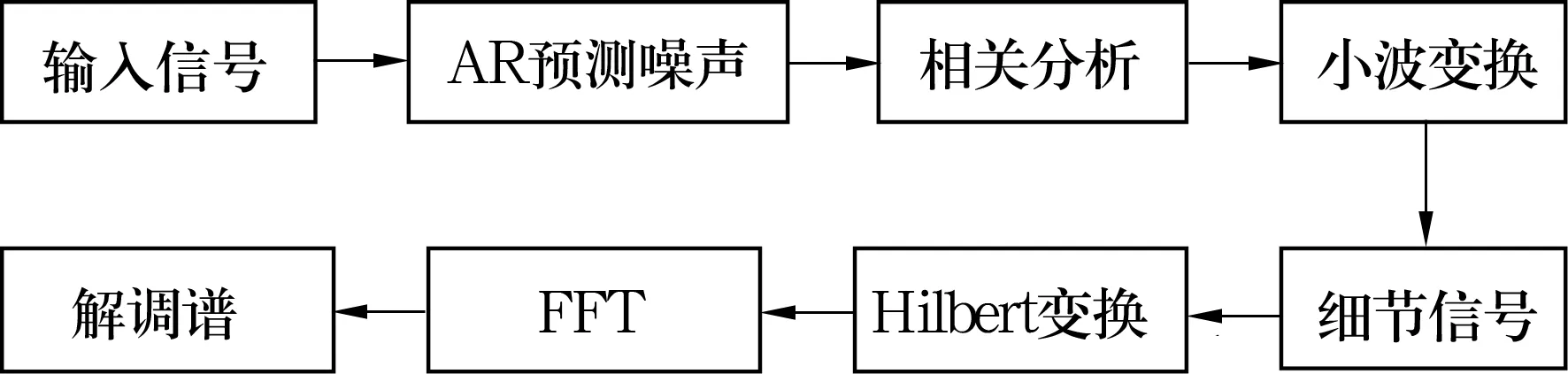
图1 方法流程图
1.2 利用AR(n)模型实现信号降噪
首先对滚动轴承故障信号进行AR(n)模型[4]降噪处理。设随机序列用{ti}表示为
xn=-∑aix(n-i)+ε(n);1≤n≤N,
(1)
式中:xn为AR序列;n为模型阶次;ε(n)为白噪声序列。
通过AIC准则来确定模型的最佳阶数。AIC准则的定义为
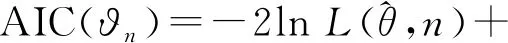
(2)

通过(1)式得到自相关序列为
Rx(k)=E{x(n)x(n+k)}=Rx(k)=-
∑aiRx(k-i);k≠0,
(3)
式中:Rx(k)为xn的自相关序列。
在(3)式中取k=m+1,m+2,…,2m,得矩阵方程
(4)
使(4)式中不包含Rx(0)项,然后用广义逆矩阵求解AR参数。将得到的参数代入(1)式中,可以得到对白噪声的预测。
1.3 基于多重相关分析的降噪
为了进一步对信号进行降噪处理,采用了多重自相关[5-6]降噪方法。设信号为
x(t)=s(t)+n(t)=Asin (ω0t+φ)+n(t) ,
(5)
式中:A为信号幅度;φ为信号初始角度;n(t)为噪声。
x(t) 的自相关函数为
x(t+τ)dt+Rn(τ) 。
(6)
通过计算得

(7)

(8)
由此递推,得出经过多次相关函数为
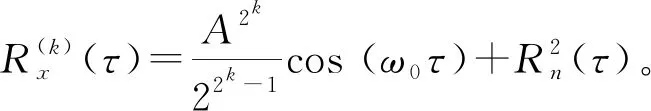
(9)
可见,信号的多重自相关函数在幅值和相位上虽然有变化,但是频率没有变化,也就是说,调幅信号的多重自相关函数仍是调幅信号,调制频率和载波频率均不变。表明多重自相关函数保留了滚动轴承的故障特征信息,因此,可以应用这种方法降低噪声,提高信噪比。
1.4 小波分析
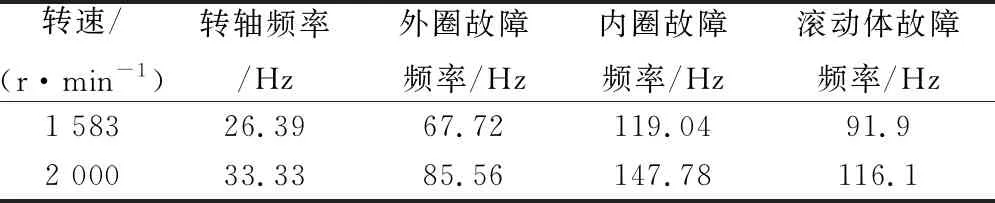
设函数ψ∈L1(R)∩L2(R),若存在常数A,B,且0 (10) 则称ψ为一个二进小波。对于小波函数ψ,令 (11) f在尺度2j和x位置的小波变换为 W2jf(x)=f⊗ψ2j(x) , (12) 称序列{Wf=W2jf(x)},j∈Z为二进小波变换,W为二进小波变换算子。W2jf(x)是f(x)在尺度2j上的细节信号。 图2 一维信号的分解与重构过程 (13) (14) 求模得到包络信号 (15) 再对包络信号进行FFT变换,得出调制解调谱。 滚动轴承故障模拟试验设备如图3所示,试验台包括调速电动机、齿轮增速器、综合电子控制系统、 4508型加速度传感器、SE系列电涡流位移传感器、USB9234数据采集器和转子故障智能诊断系统RFIDS等。将B&K加速度传感器安装在左侧故障轴承座垂直(通道3)和水平(通道2,4)位置上,电涡流位移传感器用来测转速。振动加速度信号由NI9234数据采集卡得到,试验转速通过调速电动机控制。待检测的轴承支承着转轴转动,转轴两端轴承型号为HRB6304,轴承的损伤是用电火花加工的单点损伤。试验轴承参数见表1。 图3 滚动轴承故障模拟试验台实物图 表1 试验轴承参数 选取内圈故障加以分析,外圈故障和滚动体故障以此类推。 内圈故障测试时,选取的转速为1 583 r/min 和2 000 r/min。计算得到滚动轴承各部件的特征频率见表2。 表2 滚动轴承内圈故障时各部件的特征频率 图4是转速为1 583 r/min时,分别使用小波变换、相关分析和新方法得出的解调谱。通过三者的比较不难发现,使用小波分析能够得出故障特征频率,但谐波多,故障特征频率不够突出;使用相关分析能得到内圈故障的特征频率,但故障特征频率没有外圈故障特征频率的2倍频突出;使用新方法可以明显地得出内圈故障特征频率。图5是转速为2 000 r/min时,使用3种方法得到的解调谱。从图中可以看出,只有新方法(图5c)能够识别出故障频率,其他两种方法均不能,这是因为滚动轴承故障信号十分微弱,淹没在噪声中,在包络解调谱中不能识别出故障特征频率,新方法使用AR模型、相关分析和小波分析进行多次降噪,成功提取出了滚动轴承内圈故障特征频率,证明了新方法的有效性。 图4 转速为1 583 r/min时的内圈故障解调谱 图5 转速为2 000 r/min的内圈故障解调谱 根据文献[9]提出故障频率谱线的分布特征,可以根据提出的新方法自动计算故障的特征值。其基本思路是,通过AR模型和多重自相关分析,从信号中去除噪声的影响;使用小波分析,确定分解层数和小波函数,得到细节信号;再对细节信号进行Hilbert变换,得到小波包络谱;最后在包络谱中寻找滚动轴承故障特征频率所对应的包络谱值。 设新方法得到的包络谱为W(f);F1为旋转频率包络谱值;F2为外圈频率包络谱值;F3为内圈包络谱值;F4为滚动体包络谱值。由于根据轴承转速和几何尺寸计算出的故障特征频率与实际包络谱中的故障特征频率总是存在差异,因此特征值需要在一定范围内寻找。 图6为新方法得到的包络谱特征值,由图可知,当出现外圈故障时,包络谱表现出外圈故障的特征频率,F2取值较大;当出现内圈故障时,包络谱表现出内圈故障的特征频率,F3取值较大;当出现滚动体故障时,包络谱表现出滚动体故障的特征频率,F4取值较大;当滚动轴承无故障时,包络谱上表现不出明显的滚动轴承元件特征频率,即F2,F3和F4取值较小且平均。由此可见,包络谱特征对滚动轴承故障具有较强的识别力,可用于滚动轴承智能诊断。 注:“△”表示正常情况的特征值;“*”表示外圈故障的特征值;“○”表示内圈故障的特征值;“□”表示滚动体故障的特征值。 为了验证时延相关解调和小波分析与提出新方法的统计性能,使用SVM对滚动轴承进行智能诊断。要识别滚动轴承正常状态、外圈故障、内圈故障和滚动体故障4种类型时,需要设计6个SVM分类器。首先定义y=0,表示正常状态;y=1,表示外圈故障;y=2,表示内圈故障;y=3,表示滚动体故障。利用滚动轴承试验台得到正常样本60个,内圈损伤样本69个,外圈损伤样本50个,滚动体损伤样本50个。选取每类样本中的一半作为训练样本和测试样本。 通过文中第3节提取的特征值,组成四维向量作为SVM的输入参数来识别滚动轴承的故障类型和工作状态。采用SVM识别时,使用Gauss核函数,用网格搜索的方法优化参数,其中,正则化参数C的寻优范围是[2-10,210],核函数参数g的寻优范围是[0.1,1],10折交叉验证,网格数为100,输出参数C=21.112 1,g=0.946。最终得出使用时延相关解调法得到的总识别率是88.75%,使用小波分析得到的总识别率是94.32%,使用文中提出的新方法得出的总识别率是99.16%,新方法的优越性明显。 将AR(n)模型和多重自相关分析方法引入到滚动轴承信号降噪中,再引入小波包络分析,提出了滚动轴承故障微弱信号检测新方法。与经验小波包络分析和时延相关解调法进行了对比分析,试验验证了新方法的有效性。并利用SVM对滚动轴承进行了智能诊断,试验得出新方法对故障信号的总识别率高达99.16%,故障特征提取有效性显著。
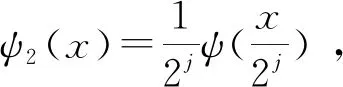
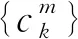

1.5 基于Hilbert变换的解调
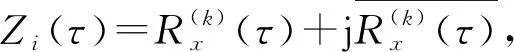

2 试验验证
2.1 试验介绍


2.2 信号分析


3 新方法包络谱自动特征提取

4 基于SVM的滚动轴承智能诊断
5 结束语
