基于Hilbert移相器和准同步算法的无功功率测量

任 晓 庞 力 方春恩 李 伟 苏育均

西华大学电气信息学院 四川 成都 610039

0 前言

随着国家智能电网建设规模的不断扩大，电力电子装置将得到广泛的应用，而由此引入的非线性元件也越来越多，势必造成电网谐波污染越来越严重[1-2]，对电网的无功功率测量带来负面影响。然而，无功功率引起电网电压和功率的损耗，关系着供电的电能质量，因此，必须对谐波（非正弦）情况下无功功率的大小进行计量和考核[3]。

C.Budeanu1972年提出了无功功率定义[4]：

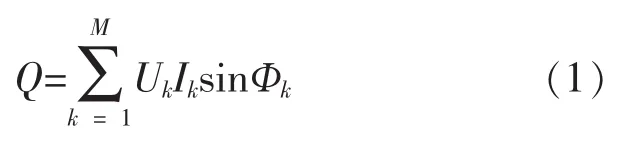
式中：Q为无功功率；Uk、Ik分别为第k次谐波的电压和电流有效值；Фk表示电压、电流的相位差；M表示高次谐波的最高次数。

根据公式（1）的定义进行无功功率测量。首先，对电压、电流的有效值分别按采样率4kHz，4.8kHz，10kHz，12.8kHz进行采样，然后经过IIR型 Hilbert移相器和准同步算法，可计算出无功功率实测值。

1 准同步算法

由于电网中谐波的存在，用准同步算法可以有效地消除同步误差，保证测量结果的精度[5-6]。

设第k次谐波分量为：

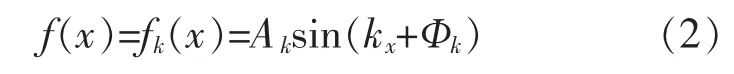
其中：k=1，2，3……。

一个周期内的平均值f（x）=fk（x）=0，将2π+σ分成N段，采样得到N个数据，采用复化的梯形公式经过k次递推可以得出k次周期的平均值为：

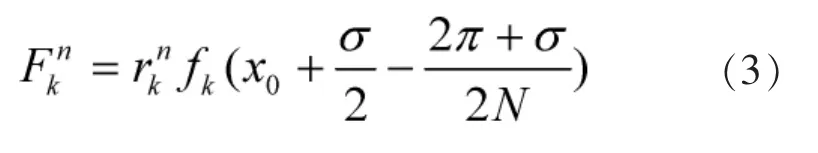
式中：σ是同步误差。

考虑一般情况：

式中：M是谐波最高次数；A0是周期平均值。显然由上述推导方法可得，

所以，limFnk=A0。

在σ，m已经确定的情况下，使｜rm｜尽可能地减小，也就能使其收敛速度加快。取n个周期进行采样，可以看出n≥3，测量精度已经很高了[5]。

2 IIR Hilbert数字移相器

理想的离散Hilbert变换的频域传递函数为[7－11]：

它是幅频特性为1，正频率成分进行－90°相移，负频率成分进行90°相移的线性变换。

在无功功率测量中，由两组Hilbert数字移相器F1和F2来实现稳定的单输入单输出滤波器系统，在关心的频带（w0，π－w0）内，｜HF1（ejw）｜＝｜HF2（ejw）｜＝1，并且实现了Hilbert的移相特性。

F1，F2传递函数满足如下关系：

式中：w0＜w＜π－w0。

Hilbert滤波器的设计一般有FIR型和IIR型两种。由于IIR滤波器阶数低，存储容量小，易于在硬件中实现等优点，所以采用IIR型Hilbert滤波器。Hilbert滤波器在所关心的频带范围内允许以为对称中心，可以由椭圆型半带滤波器设计Hilbert滤波系统。利用这种方法获得的Hilbert移相器，F1和F2是稳定的、因果的，其复频域传递函数为：

由IEC61850－9－1知电子式互感器采样频率通常为4kHz，4.8kHz，10kHz，12.8kHz。 在移相误差不大于0.0006 rad的条件下，所设计的IIR Hilbert滤波器传递函数为（以4.8kHz采样频率为例）：

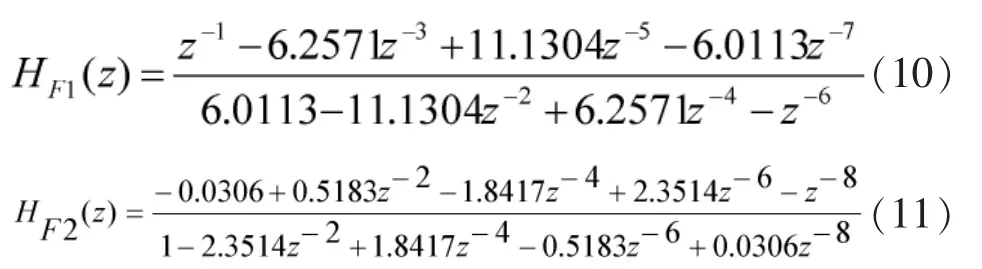
3 仿真波形

由式（10）和（11）所组成的IIR型 Hilbert数字移相器的幅频特性和相频特性分别如图1，图2所示。

图1 IIR型Hilbert移相器的幅频特性

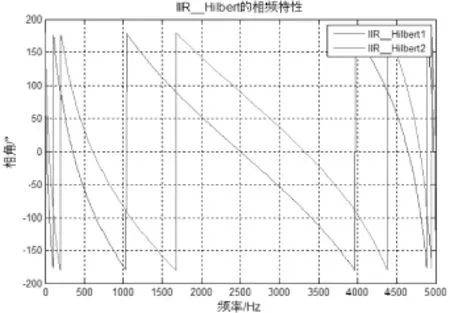
图2 IIR型Hilbert移相器的相频特性

由图1，图2可以看出，在所关心的频率范围内，整个移相系统相移接近90°，通带增益特性接近1。由此可知，在所关心的频率范围内，F1和F2两组移相器满足式（7）的要求。

4 实测结果

本文通过合并单元采样电网中电流和电压的数据，通过FPGA和DSP对算法进行处理，最终在上位机上得出的误差如表1所示。

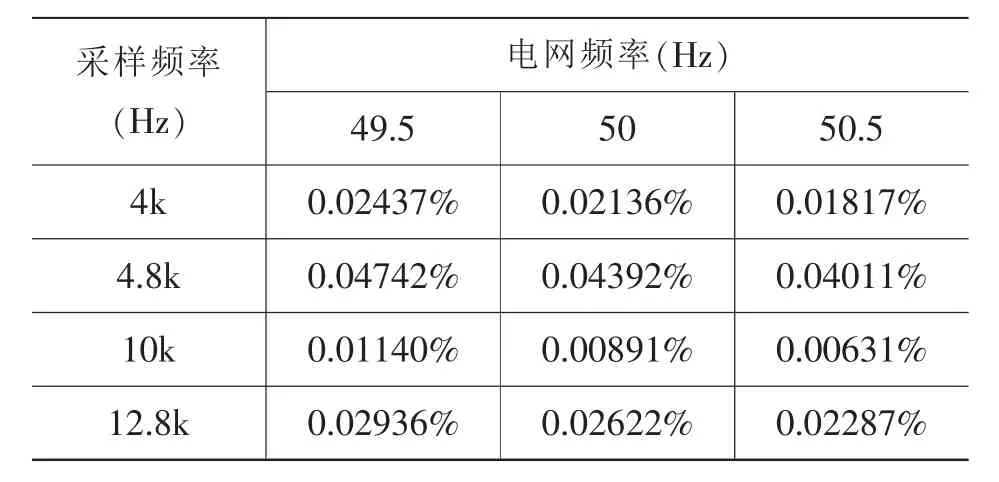
表1 不同电网频率对应的测试误差

从表1可以看出，在电网频率波动和采样频率变化的情况下，误差均小于0.05%。

5 结论

在电网中谐波情况下，利用2对IIR型Hilbert移相器和准同步算法相结合的方法来计算的无功功率，不但克服了传统无功功率算法不能用于谐波计算的缺点，而且极大的提高了无功测量的精度。

通过最后的实际数据可以看出，所设计的无功功率测量装置误差不大于0.05%，因此Hilbert移相器可以有效地应用于电网无功功率的测量。

[1] 王洪光.关于谐波处理的若干问题[J].电气应用，2009，28（11）：32-34，57.

[2] 陈啸晴.基于HILBERT数字滤波的无功功率表设计研究[D].长沙：中南大学，2009.

[3] 王薇.高精度无功功率测量的研究[D].成都：西南交通大学，2007.

[4] 庞浩，王赞基，陈建业，赵伟.基于2对Hilbert移相器的无功功率测量方法[J].电力系统自动化，2006，30（18）：45-48.

[5] 林国营.高精度多功能三相电能表[D].上海：上海交通大学，2008.

[6] 王柏林，刘华.用准同步离散Hilbert变化测量无功功率[J].电测与仪表，2003，40（456）：13-15.

[7] 吴思聪，赵威威，陈燕红.Hilbert变换在无功电能计量中的应用研究[J].电测与仪表，2009，46（522）：35-38.

[8] 庞浩，俎云霄，李东霞，王赞基.基于Hilbert移相滤波的全数字锁相环[J].电网技术，2003，27（11）：55-59.

[9] RASHID ANSARI.Elliptic Filter Design for a Class of Generalized Halfband Filters [J].IEEE TRANSACTION ON ACOUSTICS， SPEECH， AND SIGNAL PROCESSING，1985，33（4）：1146-1150.

[10] RASHID ANSARI.IIR Discrete-Time Hilbert Transformers[J].IEEE TRANSACTION ON ACOUSTICS，SPEECH，AND SIGNAL PROCESSING，1987，35（8）：1116-1119.

[11] 刘伟伟，蒋晓宇，蔡华，袁成帮.基于Hilbert变换和分类树的电能质量扰动分类辨识[J].电测与仪表，2010，47（539）：22-26，35.