汽车动力学分析及悬架子系统优化设计

刘 伟，史文库，方德广，郭福祥，桂龙明

（1.吉林大学汽车仿真与控制国家重点实验室，130022 长春，jlulw@yahoo.com.cn;2.南京依维柯汽车有限公司产品工程部，210028 南京）

汽车动力学分析及悬架子系统优化设计

刘 伟1，史文库1，方德广2，郭福祥2，桂龙明2

（1.吉林大学汽车仿真与控制国家重点实验室，130022 长春，jlulw@yahoo.com.cn;2.南京依维柯汽车有限公司产品工程部，210028 南京）

为提高汽车的行驶平顺性及操纵稳定性，在进行整车动力学分析的基础上建立汽车悬架系统多目标优化模型，并提出一种基于改进遗传算法的悬架参数多目标优化方法.该方法改进了传统遗传算法中的种群个体选择机制，锦标赛选择过程由外部非支配集和原种群同时参与，可使多次迭代所得父代种群与子代种群中的最优个体均有机会被选取，保证了新种群的多样性.以某轻型客车为研究对象，选取车身侧倾角、横摆角速度及振动加速度作为优化指标，对悬架系统的弹簧刚度、减振器阻尼系数及稳定杆扭转刚度进行多目标优化.实车实验结果表明:与悬架优化前相比，汽车行驶过程中的车身侧倾角、横摆角速度及质心振动加速度分别下降了12.3%、6.4%和9.8%.所提出的基于改进遗传算法多目标优化策略可合理匹配悬架系统各参数，改善汽车的行驶平顺性及操纵稳定性.

悬架系统;遗传算法;行驶平顺性;操纵稳定性

在悬架开发设计中，汽车行驶平顺性和操纵稳定性存在相互矛盾，单纯基于某一项性能的优化往往会导致另一性能的降低，基于汽车行驶平顺性与操纵稳定性的悬架系统多目标优化问题成为目前底盘开发设计中的重要课题［1］.汽车悬架系统多目标优化设计变量与目标函数难以用明确的数学表达式来表达，常规的多目标优化算法往往因为约束条件过于苛刻，使得求解过程变得十分复杂，优化算法迭代求解不能收敛.近年来较快发展起来的快速非支配排序遗传算法NSGA－II(Non－Dominated Sorting Genetic Algorithm)由于具有迭代求解速度快、不需人为指定共享半径等特点，已成功应用于求解各种复杂工程优化问题［2－8］.

针对汽车开发设计中平顺性和操纵稳定性无法兼顾、相互矛盾的问题，本文以某款国产轻型客车为研究对象，在建立整车转向、俯仰及侧倾运动模型的基础上，选择NSGA－II算法对该车型悬架各项刚度及阻尼参数进行多目标优化.文中所提出的改进遗传算法改进了原算法本身的锦标赛选择机制，从而保证了算法种群的多样性，使得算法的迭代求解过程更快速、有效地进行.最后，根据多目标优化结果，试制了悬架弹簧、阻尼器及稳定杆样件，并通过实车的平顺性及操纵稳定性试验，验证了本文提出的改进 NSG－II算法的有效性.

1 整车模型

为综合考虑汽车的行驶平顺性及操纵稳定性，建立整车运动模型如图1所示，包括整车转向、俯仰及侧倾运动模型.

转向运动:

俯仰运动:

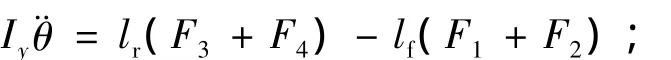
侧倾运动:

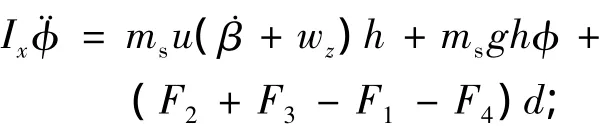
非簧载质量垂直运动:

当侧倾运动与俯仰运动都处于较小的范围内时，近似有

图1 整车动力学模型

式中:ms、mui分别为簧载质量、非簧载质量;m为整车质量;u为车速;β为质心侧偏角;wz为横摆角速度;Fy1、Fy2分别为前、后轮胎侧偏力;ksi、kti分别为悬架、轮胎刚度(i=1，2，3，4，分别表示前左、前右、后左、后右悬架，下同);kaf、kar分别为前、后悬架横向稳定杆角刚度;c1，2为前悬架阻尼系数;c3，4为后悬架阻尼系数;Ix，Iy、Iz分别为车身侧倾、俯仰及横摆转动惯量;lf、lr分别为前、后车轮到质心的距离;d为左右车轮到质心距离;h为车身侧倾高度;Φ为车身侧倾角;θ为车身俯仰角;zgi、zui、zsi分别为路面、簧载及非簧载质量位移;Fi为前、后悬架对车身作用力.

整车模型结构参数如表1所示.

表1 车辆结构参数

2 改进NSGA-II遗传算法

非支配排序遗传算法NSGA由SRINIVAS等［9］于1994年提出，采用了分级选择的方法突出种群中的优秀个体，并通过小生境方法维持优秀子种群的稳定性.KALYANMOY等在NSGA算法基础上做了进一步改进，提出了使用新的非支配排序、拥挤距离和精英选择策略的NSGA－II遗传算法.与传统的遗传算法相比，NSGA－II算法具有一定的突出优势.首先，该算法采用了新的非支配排序方法，使计算求解的迭代收敛速度大幅提高;其次，算法定义了计算迭代过程中的拥挤度距离，成功解决了传统算法中共享参数不易选择的问题;最后，算法采用了基于μ+λ选择机制的精英策略，使计算复杂度由原来的O(MN3)减少到O(MN2)，其中M代表目标的数量，N表示种群的大小［10］.

在传统的NSGA-II算法的锦标赛选择机制中，设P和Q分别为个体数目为N的父代和子代种群，算法首先合并生成一个组合的种群R=P∪Q，R中的个体数目为2N;然后根据偏序关系对个体进行排序，直到种群R中个体数目达到N，从而生成新的父代种群进行遗传操作产生新的子代种群.虽然NSGA-II算法的锦标赛选择机制可以明显改善算法的收敛性，避免丢失迭代过程中生成的最优解，但这种选择机制可能造成种群进化过程中少数个体迅速繁殖，生成较多重复个体，使得种群多样性变差.对于有较多约束条件且模型较为复杂的汽车悬架参数优化问题，这种锦标赛选择机制可能会造成进化过程中大部分非支配解都处于级数为1的非支配曲面内，而这个曲面可能远离真正的Pareto最优曲面，造成种群的迭代收敛速度下降且收敛于局部最优解.

为避免种群进化过程中重复个体大量繁殖，提高种群多样性，在精英策略中设置一个规模为M的外部非支配集D参与锦标赛选择机制［11］.改进选择机制的选取规则为

式中:ki为从种群第i个非支配分层中选取的个体数;Mi为种群第i个非支配集分层所包含的个体总数;oi为Mi的比例因子，且o=m+g/gmax(n－m)，0.5＜m ＜n＜1，g为迭代系数，gmax为迭代系数最大值;Dmax为种群非支配分层总数.

改进的NSGA-II遗传算法流程如下:

1)根据所输入悬架优化目标的初始参数［ks1，ks2，cs1，cs2］，产生规模为N的初始种群P及规模为M的外部非支配集D，并设g=0;

2)计算种群中个体的目标函数值(aw、σf1、σf2)，并进行快速非支配排序;

3)按一定的比例选择种群P中每一非支配分层中个体并与外部非支配集D一起参与锦标赛选择机制，进行种群个体的交叉和变异操作，得到子种群Q;

4)合并父代、子代种群，生成新种群R=P∪Q;

5)对新种群R进行快速非支配排序，清空D中支配个体和较密集个体.令i=1，将R中第一个非支配层个体保存到外部非支配集D中;

6)令i=i+1，返回步骤5);

7)选取群体R中前N个优秀个体作为新的种群P;

8)判断迭代系数g，若g＜gmax，则g=g+1，返回步骤2);否则算法终止，输出最优解.

3 悬架多目标参数优化模型

3.1 目标函数确定

悬架参数设计过程中，应使得车身振动加速度响应幅值尽可能较小以满足平顺性的要求，这往往需要悬架各项刚度及阻尼参数的合理匹配;与此同时，悬架也应使汽车在转弯时具有一定的抗侧倾能力，以满足操纵稳定性的要求，这就需要汽车具有较小的车身侧倾度和横摆角速度.考虑到以上目标优化目标的均衡，提出悬架多目标优化目标函数表达式为

式中，aRMS为汽车质心处的振动加速度均方根值，m/s2.

设计变量取值范围如表2所示.

表2 多目标优化变量

3.2 约束条件

1)针对悬架偏频对汽车平顺性的影响，设计前后悬架刚度约束为

式中:ff和fr分别为前后悬架偏频，Hz;ms1和ms3分别为前后悬架簧载质量，kg.

2)针对悬架阻尼比对平顺性的影响，设计前后悬架刚度及阻尼系数约束为

式中，ζf和ζr分别为前后悬架阻尼比.

3)针对车身侧倾角对操纵稳定性的影响，在侧向加速度4 m/s2下，设计车身侧倾角约束为

式中，MΦ为汽车车身的侧倾力矩，Nm;KΦ为汽车前后悬架的总侧倾刚度，Nm/°.

4)针对汽车不足转向增益对操纵稳定性的影响，设计汽车不足转向增益约束为

式中，Gr为汽车不足转向增益，δ为前轮转向角.

4 优化结果分析

为验证本文提出的改进多目标优化算法的有效性，在建立整车转向、俯仰及侧倾运动模型的基础上，分别采用NSGA-II遗传算法及改进NSGAII算法对现有悬架进行参数优化设计.定义如下计算工况:工况一，匀速行驶工况，即汽车在等级为B级的路面上以80 km/h车速匀速行驶，计算汽车质心处的振动加速度均方根值;工况二，稳态回转工况，即汽车绕半径为15 m的圆周做匀加速圆周运动，计算侧向加速度为4 m/s2时的车身侧倾角及横摆角速度值.

基于遗传算法的悬架参数多目标优化求解过程中算法参数设置如下:定义种群P规模N=500，外部非支配集D规模M=500，选取最大迭代系数gmax=200;交叉概率为0.65，变异概率为0.05.图2、3所示为原NSGA-II遗传算法与改进NSGA-II遗传算法在种群进化500代后得到的Pareto最优解集象点在目标空间中的分布情况.

图2 NSGA-II算法的优化结果

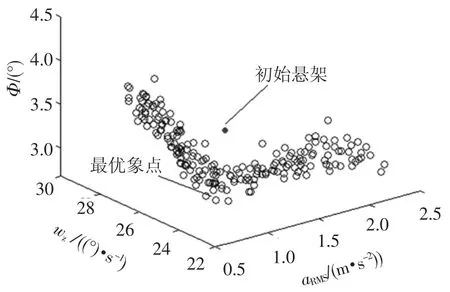
图3 改进NSGA-II算法的优化结果

由以上两图可以看出，原NSGA-II遗传算法与改进NSGA-II遗传算法均可找到一组可以使悬架平顺性及操纵稳定性指标较优的Pareto最优解集，而改进NSGA-II遗传算法由于改进了锦标赛选择机制，使得算法迭代速度更快，所获得的Pareto最优解在目标空间分布更为均匀.在目标空间中选取一组最优象点(最优解，如图2、3所示)，汽车平顺性与操纵稳定性的各项性能指标优化前后如表3所示.

表3 性能指标计算结果对比

由表3可以看出，改进NSGA-II算法求解获得的最优解优于原NSGA-II算法.

5 实车试验验证

根据优化所得的悬架参数，试制前后悬架稳定杆、阻尼器及各弹簧样件，并通过实车试验的方法验证本文所提多目标优化算法的有效性.参照国标GB/T 6263.6—94《汽车操纵稳定性试验方法稳态回转试验》，驾驶员操纵汽车以最低稳定速度沿半径15 m圆周行驶，待汽车行驶轨迹稳定后，固定转向盘不动，使汽车做匀加速运动.

试验过程中通过车速仪记录行驶车速，并通过陀螺仪记录汽车加速过程中车身侧倾角、横摆角速度及侧向加速度数值.悬架改进前后，横摆角速度及车身侧倾角时域对比曲线如图4、5所示.

图4 车身横摆角速度

图5 车身侧倾角

参考标准GB/T 4970—1996《汽车平顺性随机输入行驶试验方法》，选取汽车质心为振动加速度响应测点，使用加速度传感器测取该点处振动加速度信号用以评价悬架改进对整车振动的影响.定义试验路况为B级公路，车辆载荷条件为满载，车速为80 km/h，汽车质心处振动加速度响应情况如图6所示.

通过对比汽车质心处振动加速度、车身横摆角速度及侧倾角曲线，试验客车悬架经多目标优化后可有效衰减汽车质心处的振动加速度，并有效降低了汽车转向工况下车身横摆角速度及侧倾角幅值.悬架优化前后各性能指标试验结果对比如表4所示.

图6 汽车质心处振动加速度

表4 性能指标试验结果对比

通过对比可以看出，本文所提出的悬架多目标优化策略在改善汽车的行驶平顺性的同时兼顾操纵稳定性，可较好地解决悬架开发设计中行驶平顺性与操纵稳定性相互矛盾的问题.

6 结论

1)分析了汽车悬架系统开发设计中平顺性与操纵稳定性相互矛盾不易兼顾的问题，以某国产轻型客车为研究对象，建立了整车转向、俯仰及侧倾运动数学模型，并将NSGA－II算法引入到悬架多目标优化设计中，建立了悬架参数多目标优化模型，为解决悬架设计中平顺性与操纵稳定性相互矛盾问题提供了新的思路.

2)提出了一种改进的遗传算法种群个体选择机制.该方法改进了传统遗传算法中的种群个体选择机制，锦标赛选择过程由外部非支配集和原种群同时参与，这样可使多次迭代所得父代、子代种群中优秀个体均有机会被选取，从而保证了新种群个体的多样性.

3)实车试验表明，改进算法应用于悬架参数多目标优化设计中，明显提高算法的迭代求解速度，且兼顾了汽车悬架设计中的平顺性与操纵稳定性，取得了较好的实际应用效果.

［1］王其东，秦炜华，陈无畏.基于多自由度模型的汽车ASS与EPS集成控制研究［J］.系统仿真学报，2009，21(16):5130－5133.

［2］KANNAN S，BASKAR S，MCCALLEY J，et al.Application of NSGA-II Algorithm to Generation Expansion Planning［J］.IEEE Transactions on Power Systems，2009，24(1):454 －461.

［3］ROBERTSON D，DELAGRAMMATIKAS G J.The suspension system of the 2009 cooper union FSAE vehicle:a comprehensive design review［J］.SAE Paper，2010，2010－01－0311.

［4］张超勇，董星，王晓娟，等.基于改进非支配排序遗传算法的多目标柔性作业车间调度［J］.机械工程学报，2010，46(11):156 －164.

［5］GE HAI WEN GE，SHI YU，REITZ R D，et al.Optimization of a HSDI diesel engine for passenger cars using a multi-objective genetic algorithm and multi-dimensional modeling［J］.SAE Paper，2009，2009-01-0715.

［6］RAKHEJA S，STIHARU I.Influence of suspension kinematics and damper asymmetry on the dynamic responses of a vehicle under bump and pothole excitations［J］.SAE Paper，2010，2010 －01 －1135.

［7］管欣，逄淑一，詹军，等.汽车悬架运动学特性参数优化方法［J］.哈尔滨工业大学学报，2011，43(1):145－148.

［8］MA Kai，PANG Shuyi.Interval optimization of uncertain suspension kinematics characteristic parameters［J］.SAE Paper，2011，2011 －01 －0730.

［9］SRINIVAS N，KALYANMOY D，Multiobjective optimization using nondominated sorting in genetic algorithms［J］.Evloutionary Computation，1994，2(3):221 －248.

［10］GE Haiwen，SHI Yu，REITZ R D，et al.Heavy-duty diesel combustion optimization using Multi-objective genetic algorithm and multi-dimensional modeling ［J］.SAE Paper，2009，2009 －01 －0716.

［11］张成芬，赵彦珍，陈锋，等.基于改进NSGA-Ⅱ算法的干式空心电抗器多目标优化设计［J］.中国电机工程学报，2010，30(18):115 －121.

Vehicle dynamics analysis and optimization of suspension design

LIU Wei1，SHI Wen-ku1，FANG De-guang2，GUO Fu-xiang2，GUI Long-ming2

(1.State Key Laboratory of Automotive Simulation and Control，Jilin University，130022 Changchun，China，jlulw@yahoo.com.cn;2.Product Engineering，Nanjing IVECO Motor Company LTD，210028 Nanjing，China)

To improve vehicle ride comfort and handling stability，a multi-objective optimization strategy based on improved genetic algorithm was designed for the suspension system.As the study of a light passenger bus，taken the vehicle body side angle，yaw rate and the amplitude of vibration acceleration as optimization index，a multi-objective optimization model of suspension system parameters was established.The method improved the selection mechanism in the individual populations，and the improvements would enable the parent population and offspring population of optimal individuals to have the same opportunity to be selected to ensure diversity of new species.The real vehicle experimental results showed that:compared with the suspension before optimization，the vehicle body side angle，yaw rate and the amplitude of vibration acceleration had been reduced by 12.3%，6.4%and 9.8%.The new strategy could reasonably match the parameters of suspension system，and simultaneously improve the vehicle ride comfort and handling stability.

suspension system;genetic algorithm;ride comfort;handing stability

U463.33

A

0367－6234(2012)03－0096－06

2011－01－01.

国家高技术研究发展计划资助项目(2006AA110104).

刘 伟(1984—)，男，博士研究生;

史文库(1960—)，男，教授，博士生导师.

(编辑 杨 波)