物理竞赛中运算型难题例析

江四喜

（武汉市第二中学，湖北 武汉 430010）

在中学物理中，作为规律性的核心内容，如定理、定律之类并不是很多，而且表述也都比较简洁、明了.但物理却又是中学阶段让很多学生感觉是最难学的学科，而其难学也是很多学生最终弃理学文的主要因素.究其原因，主要是因为要学好物理，学习者必须具备较强的综合处理物理问题的能力.近年来，在各校自主招生的物理考试中，越来越多地使用竞赛试题，其主要原因就是解答物理竞赛试题的过程，能较好地展现学生处理综合问题的能力.

中学物理竞赛大纲中对物理竞赛试题的命题原则作了明确的说明，即不要求答题者使用较为复杂的高等数学知识，便能处理相关的物理问题.多年的竞赛试题表明，竞赛的命题包含了一个基本特征，就是对大学普通物理学的内容进行初等化处理，其难点大多体现在要求中学生在不使用复杂的高等数学知识的前提下，能用中学阶段所掌握的知识对普通物理的问题进行处理，因此，学生们在解答这类试题的过程中，在认清模型结构，作出过程分析，找准物理的临界问题及隐含条件的同时，还必须综合运用微元、对称、等效、类比、联想、守恒、叠加、图像等物理思想方法，对问题进行分析与处理.而这一过程对学生的能力要求很高，也就产生了所谓的难题.

中学物理竞赛中的难题，大体是从运算水平、思维角度、情景模型、过程识别及信息给予几方面进行设置.这里仅对竞赛中具有一定运算难度的习题特点，作简要阐述.

运用数学知识解决物理问题的能力，是中学物理教学对高中学生的能力要求之一.由于在全国高中物理竞赛中允许学生携带计算功能强大的计算器，即便是高次方程，利用计算器进行迭代计算，也会很快得到结果，所以，常规教学中比较突出的计算问题，已不再是竞赛物理中的问题.这样，在物理竞赛中，学生的数学运算与推理能力也就显得特别重要，这也就构成了一类难题.

事实上，很多参加物理竞赛的学生对数学的学习进度，就走在物理的前面.因为只有这样，才能保证在解答物理问题时，不至于遇到数学上的障碍.

对于学生的运算能力，着重于学生的几何、数列、三角函数、二次函数以及微元问题的处理能力.

例1.质量分布均匀的刚性杆AB、CD如图1放置，A点与水平地面接触，与地面间的静摩擦因数为μA，B、D两点与光滑竖直墙面接触，杆AB和CD接触处的静摩擦因数为μC，两杆的质量均为m，长度均为l.

（1）已知系统平衡时AB杆与墙面夹角为θ，求CD杆与墙面的夹角α应该满足的条件（用α及已知量满足的方程表示）.

（2）若 μA＝1.00，μC＝0.866，θ＝60.0°，求系统平衡时α的取值范围（用数值计算求出）.

解析：本题的模型结构清晰，属静平衡的问题.受力分析也不复杂，所用规律即为一般物体的平衡条件，但要最终得到正确的结果，没有相当熟练的运算能力，恐怕难以走到最后.

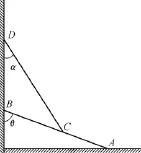
图1

建立如图2所示坐标系Oxy.两杆的受力情况：f1为地面作用于杆AB的摩擦力，N1为地面对杆AB 的支持力，f2、N2为杆AB作用于杆CD的摩擦力和支持力，N3、N4分别为墙对杆AB和CD的作用力，mg 为重力.取杆AB和CD构成的系统为研究对象，系统平衡时，由平衡条件有

以及对A点的力矩

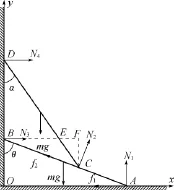
图2

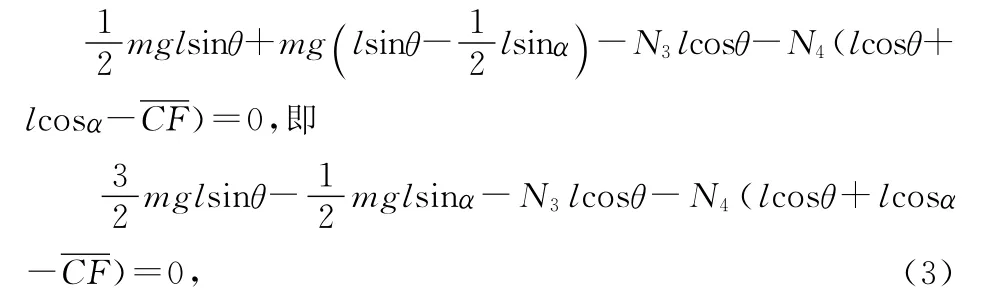
取杆CD为研究对象，由平衡条件有

以及对C点的力矩

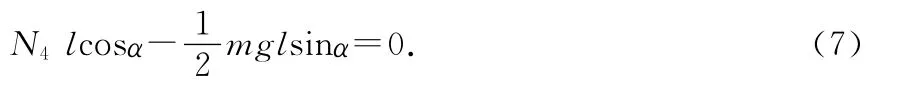
解以上各式可得

CD杆平衡的必要条件为

由（12）～（14）式得

AB杆平衡的必要条件为

由（10）、（11）、（16）式得

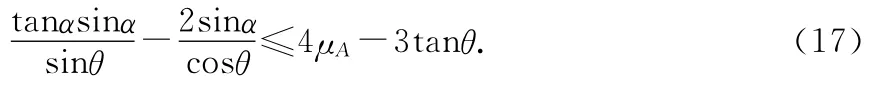
因此，使系统平衡，α应满足的条件为（15）式和（17）式.将数据代入（15）式可得α≤arctan0.385＝21.1°.将数据代入（17）式，经数值计算可得α≥19.5°.因此，α的取值范围为19.5°≤α≤21.1°.

上例的解答虽然繁杂，但只要耐心地做下去，基本上还是可解的.而有些问题，即便掌握了解答的物理方法，但其运算方法与过程仍然会让你无功而返.下面这道例题就属于这一类型.

例2.如图3，圆环之间夹有N个“三角形”，任意一线段代表电阻为R，求AB两点之间的电阻RAB.

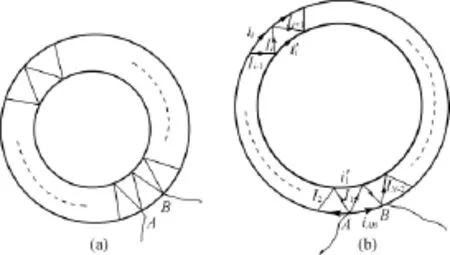
图3

解析：在图3（a）图中，两圆环中有N 个连条，设各自电流如图3（b）.

应有ii＋Ii＋ii′＝C，其中C为常数.

由iiR＝Ii－1R＋IiR，ii′R＝IiR＋Ii＋1R，得

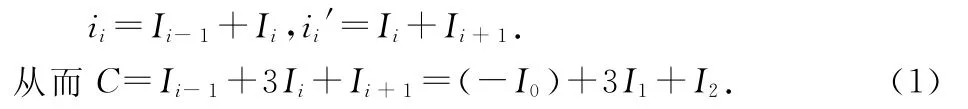
对节点A：

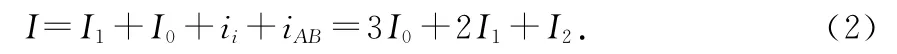
得

则对数列Ii－1＋3Ii＋Ii＋1＝C，求得通项有

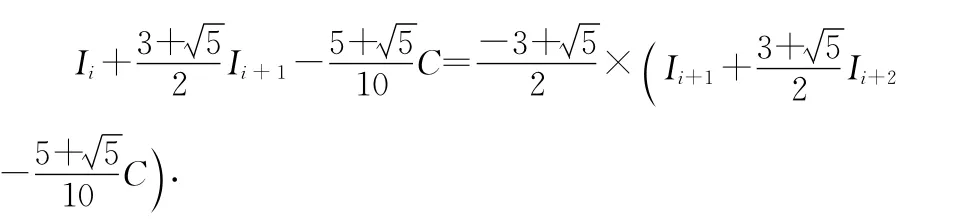
对上式由电路对称性有IN－2＝I1，IN－1＝－I0，代入C＝I－4I0＋I1，化简得

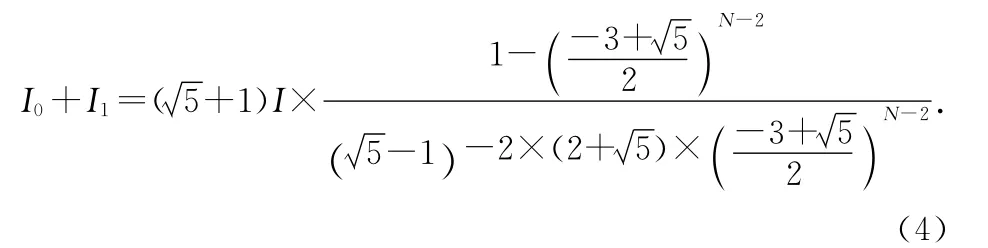
对UAB，可得UAB＝iABR 及UAB＝2I0R，UAB＝（I1＋I2＋…＋IN－2）R，则iAB＝2I0，I1＋I2＋…＋IN－3＋IN－2＝2I0.为利用3ii＋ii－1＋ii＋1＝C，再写出（－I0）＋I1＋…＋IN－3＝I0－I1.I2＋I3＋…＋IN－2＋IN－1＝I0－I1.得

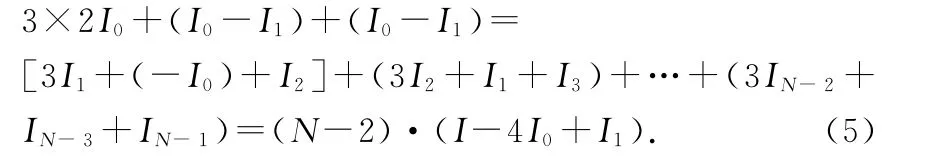
联立（4）、（5）式可得I与I0之间的关系，进而可得

除了复杂的运算，某些特殊方程的解法也是竞赛中非常重要的一个方面，而对于竞赛中可能出现的高次方程，则可利用手中功能强大的计算器进行运算.在此举一例.

例3.质量均为m的小球1、2用长为4a的轻质细线相连后，均以初速v沿着与线垂直的方向在光滑水平面上运动，开始时线处于伸直状态.在运动过程中，线上距离小球1为a的点部位与固定在水平面上的一竖直光滑细钉接触，如图4所示.设在以后的运动过程中两球不相碰，试求小球与钉的最大距离（精确到0.001a）.

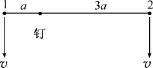
图4

解析：运动过程中小球1、2所受细线的拉力相对钉子的力矩均为0，因此小球1、2各自相对钉子的角动量都守恒.设某时刻小球1沿细线方向的速度为vr、与细线垂直方向的速度为v1θ，那么小球2沿细线方向的速度大小也为vr、与细线垂直方向的速度设为v2θ，如图5所示.小球1、2的角动量守恒式为

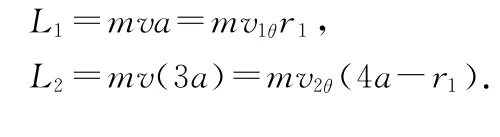
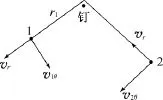
图5

式中r1为球1与细钉的距离.又因系统光滑，有动能守恒式

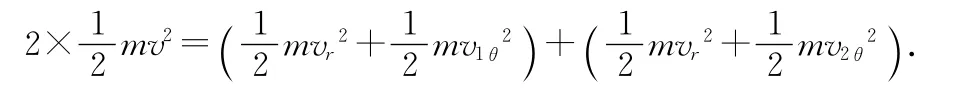
当小球1达到与铁钉最大距离时，满足条件vr＝0.代入上式得v1θ2＋v2θ2＝2v2.与角动量守恒式联立，可得

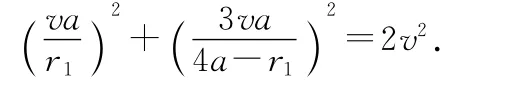
在计算器上采用二分逼近法，可得数值近似解A＝1.653.因此，小球1与钉的最大距离为r1＝1.653a.

在物理竞赛中，各类难题对问题的设置，多数情况下是交融在一起的，是不可分割的，运算难度只是其中的一项要素.如例2，对中学生而言，其模型是复杂的，思维难度也是很大的.面对这类问题，沉着地分析，规范地表述，是突破障碍的保证，也是处理物理问题能力的集中体现.